Datawhale学习笔记-吃瓜笔记:绪论与模型评估与选择
绪论
什么是机器学习
简单的说:
人工智能:让机器变得像人一样拥有智能的学科
机器学习:让计算机像人一样能从数据中学习出规律的一类算法
深度学习:神经网络类的机器学习算法
人工智能 > 机器学习 > 深度学习
人工智能具体应用领域:
计算机视觉(Computer Vision, CV):让计算机拥有视觉能力
自然语言处理(Natural Language Processing, NLP):让计算机拥有语言能力
推荐系统(Recommender System, RS):让计算机精确分析出人的喜好
稍微像样点的说:
机器学习:致力于研究如何通过计算的手段,利用经验来改善系统自身的性能,在计算机系统中,“经验”通常以“数据”形式存在,因此,机器学习所研究的主要内容,是关于在计算机上从数据中产生“模型”的算法,即“学习算法”,有了学习算法,我们把经验数据提供给它,它就能基于这些数据产生模型;在面对新的情况时,模型会给我们提供相应的判断,如果说计算机科学是研究关于“算法”的学问,那么类似的,可以说机器学习时研究关于“学习算法”的学问。
Mitcheel在1997年给出了一个更形式化的定义:假设用P来评估计算机程序在某任务类T上的性能,若一个程序通过过利用经验E在T中任务上获得的性能改善,则我们就说关于T和P,该程序对E进行了学习。
基本术语
数据集(data set):记录的集合
样本(sample)/示例(instance):单条记录【一个示例可以称为一个"特征向量(feature vector)"】
属性(attribute)/特征(feature):反映事件或对象在某方面的表现或性质的事项,例如:色泽、根蒂、敲声
属性值:属性上的取值
维度(dimensionality):单个样本所包含的属性个数
学习/训练:从数据中学得模型的过程
训练数据(training data):训练过程中使用的数据
训练集:训练样本的集合
学习器:模型
样例(example):拥有标记信息【有结果】的示例
分类(classification):预测的结果是离散值
测试(testing):学到模型后,使用其进行预测的过程称为“测试”
测试样本(testing sample):被预测的样本
验证集(validation set):评估测试的数据集
泛化(generalization)能力:模型在新样本的能力
模型评估与选择
经验误差与过拟合
通常我们把分类错误的样本数占样本总数的比例称为“错误率”,即如果在m个样本中有a个样本分类错误,则错误率E=a/m;相应的1-a/m称为“精度”(accuracy)即“精度=1-错误率”,更一般地,我们把学习器的实际预测输出与样本的真是输出之间的差异称为“误差”,学习器在训练集上的误差称为“训练误差”或“经验误差”,在新样本上的误差称为“泛化误差”
过拟合:当学习器把训练样本学的“太好”了的时候,很可能已经把训练样本自身的一些特点当作了所有潜在样本都会具有的一般性质,这样就会导致泛化性能下降。过拟合经验误差很小,但泛化误差很大(将训练样本自身的性质作为了一般性质)。过拟合只能缓解
欠拟合:与“过拟合”相对,对训练样本的一般性质尚未学好,欠拟合经验误差很大(对训练样本的一般性质尚未学好)。
导致过拟合的因素:有多种因素可能导致过拟合,最常见的情况:由于学习能力过于强大,以至于把训练样本所包含的不太一般的特性都学到了。过拟合是机器学习面临的关键障碍,各类学习算法都必然带有一些针对过拟合的措施。
导致欠拟合的因素:通常由于学习能力低下造成,欠拟合比较容易克服,可以在决策树学习中扩展分支,在神经网络学习中增加训练轮数。
评估方法
留出法
留出法直接将数据D话恩威两个互斥的集合,旗忠一个集合作为训练你S,另一个作为测试集T,即D=S∪T,S∩T=∅,在S上训练处模型后,用S上训练出模型后,用T来评估其测试误差,作为对泛化误差的估计。
训练/测试集的划分要尽可能保持数据分布的一致性,避免因数据划分过程引入额外的偏差而对最终结果产生影响。另一个需要注意的,即便在给定训练/测试集的样本比例后,仍存在多种划分方式对初始数据集D进行分割。因此,单次使用留出法得到的估计结果往往不够稳定可靠,在使用留出法时,一般采用若干次随机划分、重复进行试验评估后取平均值作为留出法的评估结果。
交叉验证法

“交叉验证法”先将数据集D划分为k个大小相似的互斥子集,即D=D1∪D2∪…Dk,Di∩Dj=∅(i≠j)每个子集Di都尽可能保持数据分布的一致性。然后,每次用k-1个子集的并集作为训练集,余下的那个子集作为测试集,这样可以获得k组训练/测试集,从而可进行k次训练和测试,最终返回的是这k个测试机过得取值。
交叉验证法评估结果的稳定性和保真性在很大重读上取决于k的取值
所以,交叉验证法也称为k折交叉验证
自助法
自助法(Bootstrap Method,Bootstrapping或自助抽样法)是一种从给定训练集中有放回的均匀抽样,也就是说,每当选中一个样本,它等可能地被再次选中并被再次添加到训练集中。自助法由Bradley Efron于1979年在《Annals of Statistics》上发表。当样本来自总体,能以正态分布来描述,其抽样分布(Sampling Distribution)为正态分布(The Normal Distribution);但当样本来自的总体无法以正态分布来描述,则以渐进分析法、自助法等来分析。采用随机可置换抽样(random sampling with replacement)。对于小数据集,自助法效果很好。
632自助法
最常用的一种是.632自助法,假设给定的数据集包含d个样本。该数据集有放回地抽样d次,产生d个样本的训练集。这样原数据样本中的某些样本很可能在该样本集中出现多次。没有进入该训练集的样本最终形成检验集(测试集)。 显然每个样本被选中的概率是1/d,因此未被选中的概率就是(1-1/d),这样一个样本在训练集中没出现的概率就是d次都未被选中的概率,即(1-1/d)。当d趋于无穷大时,这一概率就将趋近于1/e=0.368,所以留在训练集中的样本大概就占原来数据集的63.2%。
Bootstrap自助法
最常用的一种Bootstrap自助法,假设给定的数据集包含d个样本。该数据集有放回地抽样m次,产生m个样本的训练集。这样原数据样本中的某些样本很可能在该样本集中出现多次。没有进入该训练集的样本最终形成检验集(测试集)。 显然每个样本被选中的概率是1/m,因此未被选中的概率就是(1-1/m),这样一个样本在训练集中没出现的概率就是m次都未被选中的概率,即(1-1/m)m。当m趋于无穷大时,这一概率就将趋近于e-1=0.368,所以留在训练集中的样本大概就占原来数据集的63.2%。
例如:人工样本为1,2,3;只有三个样本,则可以从随机变量X,分布为P(X=k)=1/3, k=1,2,3; 这样的经验分布中用计算机根据上述分布自动产生样本,如产生5个样本:1 2 3 2 1;也可以是:3 3 2 1 1
自助法在数据集较小、难以有效划分训练集和测试集时很有用;此外,自助法能从初始数据集中产生多个不同的训练集,这对集成学习等方法有很大的好处。然而,自助法产生的数据集改变了初始数据集的分布,这会引入估计偏差。因此,在初始数据量足够时,留出法和交叉验证法更常用一些。
性能度量
错误率与精度
错误率与精度常用于分类任务,错误率是测试样本中分类错误的样本数占总样本数的比例,精度是测试样本中分类正确的样本数占总样本数的比例。
假设数据集D,模型f:
分类错误率:
E ( f ; D ) = 1 m ∑ i = 1 m I ( f ( x i ) ≠ y i ) E(f ; D)=\frac{1}{m} \sum_{i=1}^{m} \mathbb{I}\left(f\left(x_{i}\right) \neq y_{i}\right) E(f;D)=m1∑i=1mI(f(xi)=yi)
精度:
acc ( f ; D ) = 1 m ∑ i = 1 m I ( f ( x i ) = y i ) = 1 − E ( f ; D ) \begin{aligned} & \operatorname{acc}(f ; D)=\frac{1}{m} \sum_{i=1}^{m} \mathbb{I}\left(f\left(x_{i}\right)=y_{i}\right) \\ =& 1-E(f ; D) \end{aligned} =acc(f;D)=m1i=1∑mI(f(xi)=yi)1−E(f;D)
更一般地,若对于数据分布D和概率密度函数p(∙),错误率与精度可分别描述为:
E ( f ; D ) = ∫ x ∼ D I ( f ( x ) ≠ y ) p ( x ) d x acc ( f ; D ) = ∫ x ∼ D I ( f ( x ) = y ) p ( x ) d x = 1 − E ( f ; D ) \begin{array}{l} E(f ; D)=\int_{x \sim D} \mathbb{I}(f(x) \neq y) p(x) d x \\ \\ \operatorname{acc}(f ; D)=\int_{x \sim D} \mathbb{I}(f(x)=y) p(x) d x \\ \\ =1-E(f ; D) \end{array} E(f;D)=∫x∼DI(f(x)=y)p(x)dxacc(f;D)=∫x∼DI(f(x)=y)p(x)dx=1−E(f;D)
若测试数据集的精度高或错误率小,则模型的泛化能力强;反之,则泛化能力弱。
用测试数据集的精度来表示模型的泛化能力在正负样本比例相差较大的时候就不适用了。
如:
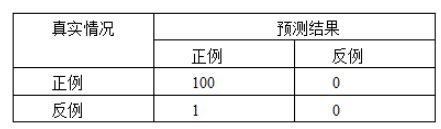
上表的混淆矩阵可知:
测试数据集正样本和负样本的比例是100:1,把所有样本都检测为正样本,准确率99%,但不能说明模型的泛化能力强,因为不能反映模型对负样本的检测能力。运用精度来表示测试数据集的泛化能力,测试数据集的正负样本比例应该均衡(1:1)。
查准率、查全率与F1
查准率和查全率书上更多的是写的“查准率”(precision)和“查全率”(recall),但是我查了些资料,更多的都是写的准确率与召回率,所以我下面都是些准确率和召回率。
准确率(查准率)
准确率的公式如下:
P = T P T P + F P P=\frac{TP}{TP+FP} P=TP+FPTP
我们不妨把字母代表的意思书写出来,那么这个公式就一目了然了。
P = 预 测 正 确 的 分 类 所 有 预 测 出 来 的 正 类 P=\frac{预测正确的分类}{所有预测出来的正类} P=所有预测出来的正类预测正确的分类
那么我们就可以总结出来准确率就是:预测出来为正类中真正的正类所占的比例。
召回率(查全率)
召回率的公式如下:
R = T P T P + F N R=\frac{TP}{TP+FN} R=TP+FNTP
还是一样把字母翻译为汉字:
R = 预 测 正 确 的 分 类 真 实 情 况 中 的 正 类 R=\frac{预测正确的分类}{真实情况中的正类} R=真实情况中的正类预测正确的分类
那么我们就可以总结出来召回率就是:预测出来正确的正类占所有真实正类的比例。
F1度量
书上写了这么一句话:查准率(准确率)和查全率(召回率)是一对矛盾的度量。一般来说,查准率(准确率)高时,查全率(召回率)往往偏低;而查全率(召回率)高时,查准率(准确率)往往偏低。
这句话我们结合上样本总数 = TP + FP + FN + TN这个公式来思考,因为在TP相同的情况下,FP高了,那么FN和TN肯定会变小,FN高了,那么FP和TN肯定会变小。
但是我们对一个算法的评估,不可能单单只考虑某一个方面的性能,所以我们需要综合考虑准确率和召回率的性能度量,于是就有了平衡点和F1度量。
平衡点很简单,就是准确率 = 召回率的点,比较这几个点与原点之间的欧氏距离得到的大小,越大的越优。
但是这样又会引出一个问题,比如有的算法更倾向于准确率,有的算法更倾向于召回率(详见书32页例子),那么这么一个简单的考虑方法显然就不适用了,于是就引出了F1度量。
F1度量是基于准确率和召回率的调和平均数的倒数由来的,其原本的公式如下:
1 F 1 = 1 2 ( 1 P + 1 R ) → F 1 = 2 × P × R P + R \frac{1}{F 1}=\frac{1}{2}\left(\frac{1}{P}+\frac{1}{R}\right) \rightarrow F 1=\frac{2 \times P \times R}{P+R} F11=21(P1+R1)→F1=P+R2×P×R
调和平均数:n个数的倒数的算数平均数
对于我们这个性能度量问题来说,我们肯定是综合考虑准确率和召回率,那么我们引入这样的惩罚机制就不会使得过小的值发不出声音,从而使评估变得更准确。
当然,书上还有Fβ这个加权调和平均,主要是能够更好地衡量召回率与准确率的平均值。(我个人认为在实际运用中这个β其实也可以在算法中训练,看算法更倾向于召回率还是准确率)
1 F β = 1 1 + β 2 ( 1 P + β 2 R ) → F β = ( 1 + β 2 ) × P × R ( β 2 × P ) + R \frac{1}{F_{\beta}}=\frac{1}{1+\beta^{2}}\left(\frac{1}{P}+\frac{\beta^{2}}{R}\right) \rightarrow F_{\beta}=\frac{\left(1+\beta^{2}\right) \times P \times R}{\left(\beta^{2} \times P\right)+R} Fβ1=1+β21(P1+Rβ2)→Fβ=(β2×P)+R(1+β2)×P×R
参考资料
1.西瓜书《机器学习》,周志华
2.公式编辑器:https://latex.codecogs.com/eqneditor/editor.php
3.图片转MARKDOWN公式:https://latexlive.com/home##