我们知道在 JS 中,删除数组元素有两个方法:pop 与 shift,分别可以删除末尾与开头的元素。
然而同样是删除元素,它们的执行时间确实不同的。
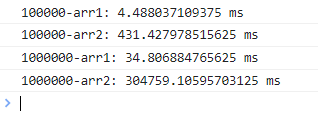
当数组项目较多时,shift 的执行时间明显长于 pop。
const test = (arrLength) => {
let arr1 = []
console.time(`${arrLength}-arr1`)
for (let i = 0; i < arrLength; i++) {
arr1.push(i)
}
for (let i = 0; i < arrLength; i++) {
arr1.pop()
}
console.timeEnd(`${arrLength}-arr1`)
let arr2 = []
console.time(`${arrLength}-arr2`)
for (let i = 0; i < arrLength; i++) {
arr2.push(i)
}
for (let i = 0; i < arrLength; i++) {
arr2.shift()
}
console.timeEnd(`${arrLength}-arr2`)
}
test(10 ** 5)
test(10 ** 6)结果如下:
这是因为 pop 删除元素后不需要改变其他元素的索引,时间复杂度为 O(1);而调用 shift 方法删除开头元素后,需要维护数组的索引,相当于对数组中的所有元素都进行了一次赋值操作,其时间复杂度为 O(n)
栈与队列
栈与队列是我们常用的两种数据结构。
栈的元素先进后出,比如函数栈,函数递归调用时,后调用的函数先执行完。
队列的元素先进先出,比如任务队列,任务按照派发的顺序依次执行。
在 JS 中,栈可以看成只调用 push 与 pop 方法的数组,队列可以看成是只调用 shift 与 push 方法的数组。
然而在之前的例子中也看到了,当处理大量数据时,把数组直接当成队列使用性能非常差。
所以,我们要设法实现队列这一数据结构。
如何实现?
开始之前我们要明确实现的目标,我们实现的队列要提供以下几个功能:
- 存储数据:队列要能够按序存储数据
push:添加元素的唯一方法,将元素添加进队列尾部的方法,并返回队列长度shift:删除元素的唯一方法,将队首元素删除的方法,并返回删除的元素length:可以通过 length 属性访问队列的长度- 访问元素:一般队列会允许访问队头与队尾的元素
这里介绍通过 假删除数组元素 的方式实现队列。
我们知道数组的不能当作队列使用的原因是直接使用 shift 删除元素后会移动其余元素的索引。
我们可以自己维护数组的索引,避免删除后频繁移动。
具体实现是定义一个 offset 变量,记录索引的偏移。
在访问元素时,通过偏移量的计算,获取正确的结果。
在删除元素时,只用把数组首元素置空,然后偏移加 1。
这期间不进行真实的删除操作,这就是所谓的假删除。
但为了避免数组大小无限增大,我们设置当偏移量(空元素)大于数组的长度的一半时,就将空元素删除,保证占用空间不超过使用队列大小的两倍。
具体实现代码及注释如下
// 创建一个队列
function createQueue() {
const arr = [] // 内部的数组
let offset = 0 // 偏移
// 添加元素,返回队列的长度
const push = (...arg) => {
return arr.push(...arg) - offset
}
// 删除元素,返回被删除的元素
const shift = () => {
const res = arr[offset] // 要返回的删除元素
// 假删除
arr[offset] = undefined
offset++
// 避免数组无限扩大,定期一次性删除前面的空元素
if (offset > arr.length / 2) {
arr.splice(0, offset)
offset = 0
}
return res
}
// 通过 Proxy 拦截队列的操作
const p = new Proxy(
{},
{
get(target, prop) {
switch (prop) {
case 'push': {
return push
}
case 'shift': {
return shift
}
case 'length': {
// 队列长度 = 数组实际长度 - 偏移
return arr.length - offset
}
default: {
// 元素真实索引 = 要访问的索引 + 偏移
return arr[Number(prop) + offset]
}
}
},
}
)
return p
}
const queue = createQueue()
console.log(queue.push(0, 1, 2, 3, 4)) // 5
console.log(queue[0]) // 0
console.log(queue.length) // 5
console.log(queue.shift()) // 0
console.log(queue[0]) // 1
console.log(queue.length) // 4
console.log(queue.shift()) // 1
console.log(queue.push(5)) // 4
console.log(queue[0]) // 2
console.log(queue[queue.length - 1]) // 5测试性能
进行 10/100/1000 万次增删操作,测试队列的性能
const test = (arrLength) => {
let arr1 = []
console.time(`${arrLength}-arr1`)
for (let i = 0; i < arrLength; i++) {
arr1.push(i)
}
for (let i = 0; i < arrLength; i++) {
arr1.pop()
}
console.timeEnd(`${arrLength}-arr1`)
let arr2 = createQueue()
console.time(`${arrLength}-arr2`)
for (let i = 0; i < arrLength; i++) {
arr2.push(i)
}
for (let i = 0; i < arrLength; i++) {
arr2.shift()
}
console.timeEnd(`${arrLength}-arr2`)
}
test(10 ** 5)
test(10 ** 6)
test(10 ** 7)
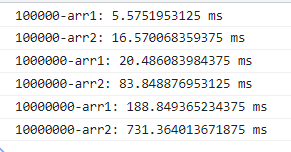
function createQueue() {……}测量结果如下:
可以看出,不管数据多大,性能也只差 4 倍。
因为要进行操作的拦截与索引偏移的计算,格外的性能开销不可避免,常数倍的性能差距已经可以满足要求。
结语
如果文中有不理解或不严谨的地方,欢迎评论提问。
如果喜欢或有所启发,希望能点赞关注,鼓励一下作者。