2022对比学习（Contrastive Learning）在各大顶会上的最新研究进展

推荐系统重在挖掘用户偏好，无论是针对数据稀疏、噪声问题或是增强其他效果，对比学习无疑是锦上添花。观察22年的推荐顶会的相关论文，我们可以观察到对比学习出现的频率明显增高，并且各种改进也层出不穷，具有多样化发展的趋势，包括但不限于

• 图数据增强方式的改进（NodeDrop、EdgeDrop、随机游走、引入辅助信息的drop）；
• 基于多视图的对比学习（例如在图的结构视图、语义视图、解耦子图间进行对比学习，可以应用到社交网络，知识图谱、bundle推荐、跨域推荐等方向）；
• 利用节点关系进行对比任务（利用节点与邻居节点的关系作为样本选取准则、可以考虑GNN节点在不同层的输出表示间的关系、超图）；
• 其他角度的对比学习任务（例如，对embedding添加噪声）。

本文从22年的顶会上选取了5篇采用对比学习的推荐相关论文与大家分享~

一、NCL

论文标题：Improving Graph Collaborative Filtering with Neighborhood-enriched Contrastive Learning

论文来源：WWW’22

论文链接： https://doi.org/10.1145/34854...

代码链接：https://github.com/RUCAIBox/NCL

1 NCL核心思想

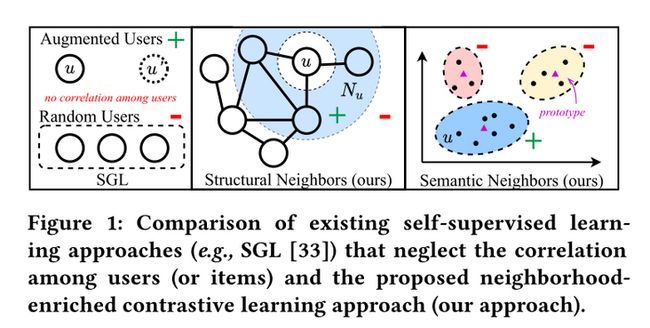
利用用户交互历史信息构建的二部图，节点关系可以分为四种：1. 相似用户；2. 相似物品；3. 用户-物品交互关系；4. 具有相似语义关系（例如用户意图等）。大多数推荐任务围绕用户-物品交互关系展开，而对同质节点之间的结构关系考虑较少，对语义关系考虑的次数则更少。NCL创新点则在于利用推荐系统中节点的潜在关系设计对比学习任务（包括结构关系与语义关系）。

在这里我们重点阐释如何去构建这两种对比学习任务，完整具体的算法细节还请大家观看原文~

2 算法细节

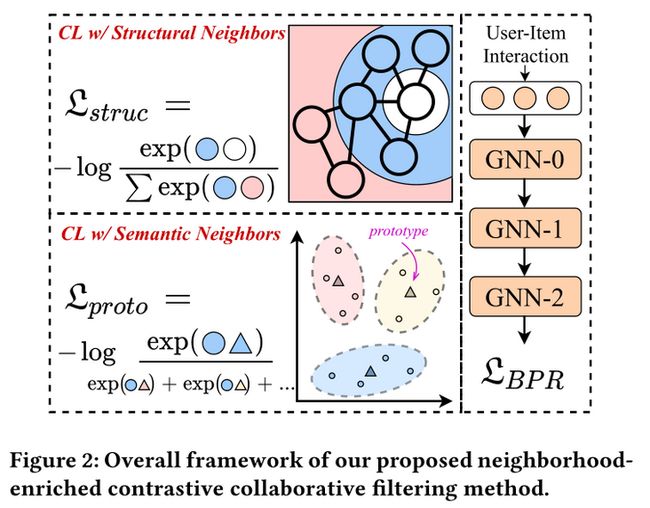
节点级的对比学习任务针对于每个节点进行两两学习，这对于大量邻居来说是极其耗时的，考虑效率问题，文章学习了每种邻居的单一代表性embedding，这样一个节点的对比学习就可以通过两个代表性embedding（结构、语义）来完成。

构建基于节点结构关系的对比学习任务：将每个用户（物品）与它的结构邻居进行对比。

由于GNN的第$k$层输出包含了$k$-hop邻居的聚合信息，而基于交互二部图的GNN模型的信息在图上经过偶数次传播，则可以聚合同质节点的邻居信息。

因此，为了避免构建其他图，我们直接利用GNN的第$k$层输出作为一个节点的$k$-hop邻居的表示，将节点自身的embedding和偶数层GNN的相应输出的embedding视为正样本对：

$$ \mathcal{L}_{S}^{U}=\sum_{u \in \mathcal{U}}-\log \frac{\exp \left(\left(\mathbf{z}_{u}^{(k)} \cdot \mathbf{z}_{u}^{(0)} / \tau\right)\right)}{\sum_{v \in \mathcal{U}} \exp \left(\left(\mathbf{z}_{u}^{(k)} \cdot \mathbf{z}_{v}^{(0)} / \tau\right)\right)} $$

$$ \mathcal{L}_{S}^{I}=\sum_{i \in I}-\log \frac{\exp \left(\left(\mathbf{z}_{i}^{(k)} \cdot \mathbf{z}_{i}^{(0)} / \tau\right)\right)}{\sum_{j \in I} \exp \left(\left(\mathbf{z}_{i}^{(k)} \cdot \mathbf{z}_{j}^{(0)} / \tau\right)\right)} $$

$$ \mathcal{L}_{S}=\mathcal{L}_{S}^{U}+\alpha \mathcal{L}_{S}^{I} $$

构建基于节点语义关系的对比学习任务：将每个用户（物品）与它具有相似语义关系的节点进行对比。这里具有语义关系指的是，图上不可到达，但具有相似物品特征、用户偏好等的节点。

怎么识别具有相同语义的节点呢？我们认为相似的节点倾向于落在临近的embedding空间中，而我们的目标就是寻找代表一组语义邻居的中心（原型）。因此，我们对节点embedding应用聚类算法去获取用户或物品的原型。

由于这个过程不可以端到端优化，我们用EM算法学习提出的语义原型对比任务。形式上，GNN模型的目标是最大化对数似然函数：

$$ \sum_{u \in \mathcal{U}} \log p\left(\mathbf{e}_{u} \mid \Theta, \mathbf{R}\right)=\sum_{u \in \mathcal{U}} \log \sum_{\mathbf{c}_{i} \in C} p\left(\mathbf{e}_{u}, \mathbf{c}_{i} \mid \Theta, \mathbf{R}\right) $$

其中，$c_i$是用户$u$的潜在原型。采用基于InfoNCE来最小化以下函数：

$$ \mathcal{L}_{P}^{U}=\sum_{u \in \mathcal{U}}-\log \frac{\exp \left(\mathbf{e}_{u} \cdot \mathbf{c}_{i} / \tau\right)}{\sum_{\mathbf{c}_{j} \in C} \exp \left(\mathbf{e}_{u} \cdot \mathbf{c}_{j} / \tau\right)} $$

$$ \mathcal{L}_{P}^{I}=\sum_{i \in \mathcal{I}}-\log \frac{\exp \left(\mathbf{e}_{i} \cdot \mathbf{c}_{j} / \tau\right)}{\sum_{\mathbf{c}_{t} \in C} \exp \left(\mathbf{e}_{i} \cdot \mathbf{c}_{t} / \tau\right)} $$

$$ \mathcal{L}_{P}=\mathcal{L}_{P}^{U}+\alpha \mathcal{L}_{P}^{I} $$

优化

总体损失函数为：

$$ \mathcal{L}=\mathcal{L}_{B P R}+\lambda_{1} \mathcal{L}_{S}+\lambda_{2} \mathcal{L}_{P}+\lambda_{3}\|\Theta\|_{2} $$

其中，由于$\mathcal{L}_{P}$不可以端到端优化，采用EM算法。利用Jensen不等式得到上述最大化对数似然函数的下界（LB）：

$$ L B=\sum_{u \in \mathcal{U}} \sum_{\mathbf{c}_{i} \in C} Q\left(\mathbf{c}_{i} \mid \mathbf{e}_{u}\right) \log \frac{p\left(\mathbf{e}_{u}, \mathbf{c}_{i} \mid \Theta, \mathbf{R}\right)}{Q\left(\mathbf{c}_{i} \mid \mathbf{e}_{u}\right)} $$

$Q\left(\mathbf{c}_{i} \mid \mathbf{e}_{u}\right)$表示观察到$e_u$时，潜在变量$c_i$的分布。

E步：采用$k$-means进行聚类得到不同节点embedding对应的聚类中心。若$e_u$属于聚类$c_i$，则$\hat{Q}\left(\mathbf{c}_{i} \mid \mathbf{e}_{u}\right) = 1$，反之为0。

M步：得到聚类中心，目标函数重写为：

$$ \mathcal{L}_{P}^{U}=-\sum_{u \in \mathcal{U}} \sum_{\mathbf{c}_{i} \in C} \hat{Q}\left(\mathbf{c}_{i} \mid \mathbf{e}_{u}\right) \log p\left(\mathbf{e}_{u}, \mathbf{c}_{i} \mid \Theta, \mathbf{R}\right) $$

假设用户在所有聚类上的分布是各向同性高斯分布。因此，函数可以写成：

$$ \mathcal{L}_{P}^{U}=-\sum_{u \in \mathcal{U}} \log \frac{\exp \left(-\left(\mathbf{e}_{u}-\mathbf{c}_{i}\right)^{2} / 2 \sigma_{i}^{2}\right)}{\sum_{\mathbf{c}_{j} \in C} \exp \left(-\left(\mathbf{e}_{u}-\mathbf{c}_{j}\right)^{2} / 2 \sigma_{j}^{2}\right)} $$

完整算法：

3 实验结果

论文的实验结果可以说是很震撼一张大表······但结果属实不错，在五个数据集上的结果证明NCL的有效性，尤其是在Yelp和Amazon book数据集上，与其他模型相比，性能分别提高了26%和17%。

二、ICL

论文标题：Intent Contrastive Learning for Sequential Recommendation

论文来源：WWW’22

论文链接：https://doi.org/10.1145/34854...

代码链接： https://github.com/salesforce...

1 ICL核心思想

很有趣的一点，这篇文章所提模型简称ICL和上篇NCL很像啊······

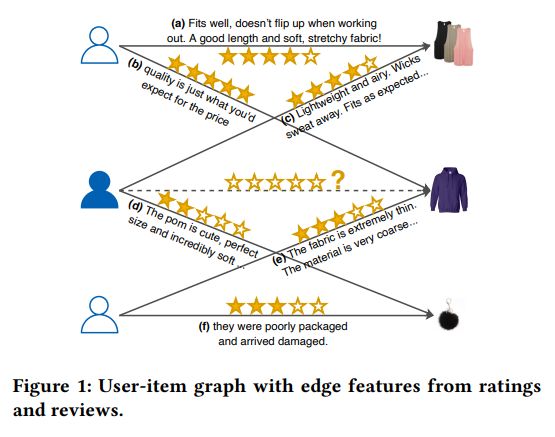
以下图作引，我们直观理解这篇文章的思想。Figure 1中展现了两个用户的购物序列，尽管没有出现一样相同的商品，但是他们最后却购买了同样的物品。原因很简单，因为他俩同为钓鱼爱好者，购买意图冥冥中含有不可言说的关系。

正是因此，我们必须重视不同用户购买序列之间的潜在意图关系。文章提出的一个良好的解决方案是，我们从未标记的用户行为序列中学习用户的意图分布函数，并使用对比学习优化SR模型。具体来说，我们引入一个潜在变量来表示用户的意图，并通过聚类学习潜在变量的分布函数。

2 算法细节

这篇文章的重要价值之一：模型图画的很漂亮，深得我心。从图中可以看出，模型采用EM算法进行优化，在E步中进行聚类，在M步进行损失函数的计算和参数更新。

重在体会思想，详细步骤解释请参照原文。

假设有$K$个用户潜在意图$\left\{c_{i}\right\}_{i=1}^{K}$，则目标公式可以改写为：

$$ \theta^{*}=\underset{\theta}{\arg \max } \sum_{u=1}^{N} \sum_{t=1}^{T} \ln \mathbb{E}_{(c)}\left[P_{\theta}\left(s_{t}^{u}, c_{i}\right)\right] $$

由于上述公式优化复杂，根据EM思想，构造下界函数，并使下界最大化：

$$ \begin{aligned} \sum_{u=1}^{N} \sum_{t=1}^{T} \ln \mathbb{E}_{(c)}\left[P_{\theta}\left(s_{t}^{u}, c_{i}\right)\right] &=\sum_{u=1}^{N} \sum_{t=1}^{T} \ln \sum_{i=1}^{K} P_{\theta}\left(s_{t}^{u}, c_{i}\right) \\ &=\sum_{u=1}^{N} \sum_{t=1}^{T} \ln \sum_{i=1}^{K} Q\left(c_{i}\right) \frac{P_{\theta}\left(s_{t}^{u}, c_{i}\right)}{Q\left(c_{i}\right)} \end{aligned} $$

根据Jensen不等式，得到

$$ \begin{array}{l} \geq \sum_{u=1}^{N} \sum_{t=1}^{T} \sum_{i=1}^{K} Q\left(c_{i}\right) \ln \frac{P_{\theta}\left(s_{t}^{u}, c_{i}\right)}{Q\left(c_{i}\right)} \\ \propto \sum_{u=1}^{N} \sum_{t=1}^{T} \sum_{i=1}^{K} Q\left(c_{i}\right) \cdot \ln P_{\theta}\left(s_{t}^{u}, c_{i}\right) \end{array} $$

简单起见，在优化下界时，我们只关注最后一个位置步骤，下界定义为：

$$ \sum_{u=1}^{N} \sum_{i=1}^{K} Q\left(c_{i}\right) \cdot \ln P_{\theta}\left(S^{u}, c_{i}\right) $$

其中$Q\left(c_{i}\right)=P_{\theta}\left(c_{i} \mid S^{u}\right)$。

为了学习意图分布$Q(c)$，利用编码器将序列得到表示$\left\{h^{u}\right\}_{u=1}^{|U|}$，并在学习到的表示上进行$k$-means聚类，从而得到$P_{\theta}\left(c_{i} \mid S^{u}\right)$。

$$ Q\left(c_{i}\right)=P_{\theta}\left(c_{i} \mid S^{u}\right)=\left\{\begin{array}{lc} 1 & \text { if } S^{u} \text { in cluster } i \\ 0 & \text { else } \end{array}\right. $$

得到意图分布$Q(c)$，下一步需要求得$P_{\theta}\left(S^{u}, c_{i}\right)$。假设意图满足均匀分布，且给定意图$c$时，$S^u$的条件分布和$L_2$标准化的高斯分布同向，则可把$P_{\theta}\left(S^{u}, c_{i}\right)$改写为：

$$ \begin{aligned} P_{\theta}\left(S^{u}, c_{i}\right) &=P_{\theta}\left(c_{i}\right) P_{\theta}\left(S^{u} \mid c_{i}\right)=\frac{1}{K} \cdot P_{\theta}\left(S^{u} \mid c_{i}\right) \\ & \propto \frac{1}{K} \cdot \frac{\exp \left(-\left(\mathbf{h}^{u}-\mathbf{c}_{i}\right)^{2}\right)}{\sum_{j=1}^{K} \exp \left(-\left(\mathbf{h}_{i}^{u}-\mathbf{c}_{j}\right)^{2}\right)} \\ & \propto \frac{1}{K} \cdot \frac{\exp \left(\mathbf{h}^{u} \cdot \mathbf{c}_{i}\right)}{\sum_{j=1}^{K} \exp \left(\mathbf{h}^{u} \cdot \mathbf{c}_{j}\right)}, \end{aligned} $$

求得下界最大化即相当于最小化以下损失函数：

$$ -\sum_{v=1}^{N} \log \frac{\exp \left(\operatorname{sim}\left(\mathbf{h}^{u}, \mathbf{c}_{i}\right)\right)}{\sum_{j=1}^{K} \exp \left(\operatorname{sim}\left(\mathbf{h}^{u}, \mathbf{c}_{j}\right)\right)} $$

可以发现，上式最大化了一个单独序列与其相应意图之间的互信息。我们为每个序列通过增强构建用于对比学习的正样本，然后优化以下损失函数：

$$ \mathcal{L}_{\mathrm{ICL}}=\mathcal{L}_{\mathrm{ICL}}\left(\tilde{\mathbf{h}}_{1}^{u}, \mathbf{c}_{u}\right)+\mathcal{L}_{\mathrm{ICL}}\left(\tilde{\mathbf{h}}_{2}^{u}, \mathbf{c}_{u}\right) $$

$$ \mathcal{L}_{\mathrm{ICL}}\left(\tilde{\mathbf{h}}_{1}^{u}, \mathbf{c}_{u}\right)=-\log \frac{\exp \left(\operatorname{sim}\left(\tilde{\mathbf{h}}_{1}^{u}, \mathbf{c}_{u}\right)\right)}{\sum_{n e g} \exp \left(\operatorname{sim}\left(\tilde{\mathbf{h}}_{1}^{u}, \mathbf{c}_{n e g}\right)\right)}, $$

其中，$c_{neg}$为一个batch中的所有意图，而同一个batch中的用户可能有相同的意图，故为了减轻假阴性的影响，将上式改为：

$$ \mathcal{L}_{\mathrm{ICL}}\left(\tilde{\mathbf{h}}_{1}^{u}, \mathbf{c}_{u}\right)=-\log \frac{\exp \left(\operatorname{sim}\left(\tilde{\mathbf{h}}_{1}^{u}, \mathbf{c}_{u}\right)\right)}{\sum_{v=1}^{N} \mathbb{1}_{v \notin \mathcal{F}} \exp \left(\operatorname{sim}\left(\tilde{\mathbf{h}}_{1}, \mathbf{c}_{v}\right)\right)}, $$

最终，模型损失函数为：

$$ \mathcal{L}=\mathcal{L}_{\text {NextItem }}+\lambda \cdot \mathcal{L}_{\mathrm{ICL}}+\beta \cdot \mathcal{L}_{\mathrm{SeqCL}} $$

完整算法：

3 实验结果

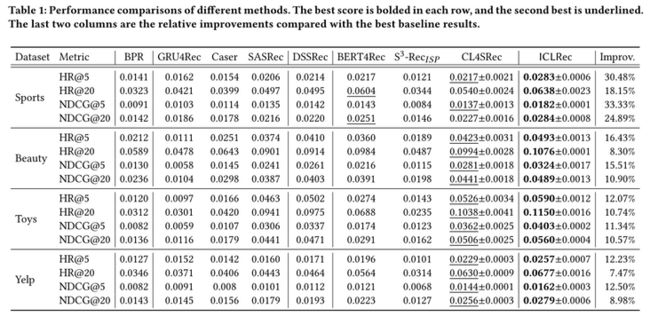
可以看出，ICLRec在所有数据集上始终优于现有方法。与最佳baseline相比，HR和NDCG的平均改善率在7.47%到33.33%之间。

三、RGCL

论文标题：A Review-aware Graph Contrastive Learning Framework for Recommendation

论文来源：SIGIR’22

论文链接：https://doi.org/10.1145/34774...

1 RGCL核心思想

这篇论文的创新点是引入了用户评分和评论作为辅助信息，为了将二者更好地融入图结构中，RGCL以交互评论作为图的边信息，并以此为基础设计了两个分别基于节点增强和边增强的对比学习任务。

2 算法细节

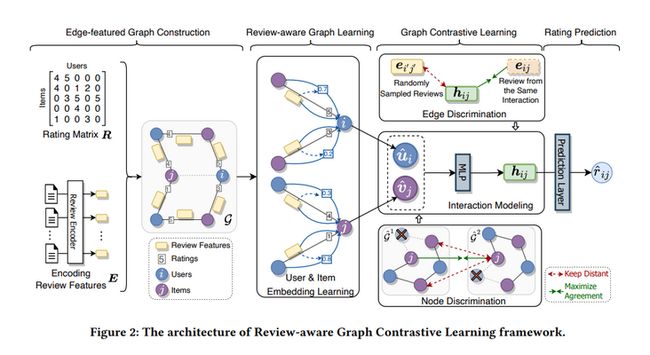
模型图可以说画的是通俗易懂，我们对照图来依次看一下每个模块~

具有特征边的图构建：从Figure 2中的图构建部分我们可以看到，用户物品交互评分矩阵$R$与评论$E$组成用户物品交互$\varepsilon=\{R, E\}$，而基于评论的推荐数据表示为具有特征边的二部图$\mathcal{G}=\langle\mathcal{U} \cup \mathcal{V}, \mathcal{E}\rangle$。

评论感知图学习：利用评分区分边的类型，评论的表示$e_{ij}$需要由BERT-Whitening生成。这里介绍如何利用基于特征边的图学习节点表示。

1. 评论感知信息传递公式为：

$$ \boldsymbol{x}_{r ; j \rightarrow i}^{(l)}=\frac{\sigma\left(\boldsymbol{w}_{r, 1}^{(l) \top} \boldsymbol{e}_{i j}\right) \boldsymbol{W}_{r, 1}^{(l)} \boldsymbol{e}_{i j}+\sigma\left(\boldsymbol{w}_{r, 2}^{(l) \top} \boldsymbol{e}_{i j}\right) \boldsymbol{W}_{r, 2}^{(l)} \boldsymbol{v}_{j}^{(l-1)}}{\sqrt{\left|\mathcal{N}_{j}\right|\left|\mathcal{N}_{i}\right|}}\\ x_{r ; i \rightarrow j}^{(l)}=\frac{\sigma\left(\boldsymbol{w}_{r, 1}^{(l) \top} \boldsymbol{e}_{i j}\right) \boldsymbol{W}_{r}^{(l)} \boldsymbol{e}_{i j}+\sigma\left(\boldsymbol{w}_{r, 2}^{(l) \top} \boldsymbol{e}_{i j}\right) \boldsymbol{W}_{r, 2}^{(l)} \boldsymbol{u}_{i}^{(l-1)}}{\sqrt{\left|\mathcal{N}_{i}\right|\left|\mathcal{N}_{j}\right|}} $$

2. 消息聚合：

$$ \boldsymbol{u}_{i}^{(l)}=\boldsymbol{W}^{(l)} \sum_{r \in \mathcal{R}} \sum_{k \in \mathcal{N}_{i, r}} x_{r ; k \rightarrow i}^{(l)}, \quad v_{j}^{(l)}=W^{(l)} \sum_{r \in \mathcal{R}} \sum_{k \in \mathcal{N}_{j, r}} x_{r ; k \rightarrow j}^{(l)} $$

3. 得到用户和物品最终表示：

$$ \hat{\boldsymbol{u}}_{i}=\boldsymbol{u}_{i}^{(L)}, \quad \hat{\boldsymbol{v}}_{j}=\boldsymbol{v}_{j}^{(L)} $$

交互建模：区别于一般推荐采用的内积预测方式，论文采用MLP学习用户物品的交互特征，并根据得到的交互特征预测评分（此处的预测评分在对比学习部分会用到）：

$$ \boldsymbol{h}_{i j}=\operatorname{MLP}\left(\left[\hat{\boldsymbol{u}}_{i}, \hat{v}_{j}\right]\right) $$

$$ \hat{r}_{i j}=\boldsymbol{w}^{\top} \boldsymbol{h}_{i j} $$

两种对比学习任务：增强节点embedding学习和增强交互建模。

基于节点的数据增强采用的是node drop，指定概率随机丢弃物品节点和相应的评论特征：

$$ \mathcal{L}_{3}^{\text {user }}=-\mathbb{E}_{\mathcal{U}}\left[\log \left(F\left(\hat{u}_{i}^{1}, \hat{u}_{i}^{2}\right)\right)\right]+\mathbb{E}_{\mathcal{U} \times \mathcal{U}^{\prime}}\left[\log \left(F\left(\hat{u}_{i}^{1}, \hat{u}_{i^{\prime}}^{2}\right)\right)\right] $$

损失为：$\mathcal{L}_{3}=\mathcal{L}_{3}^{\text {user }}+\mathcal{L}_{3}^{\text {item }}$。

增强交互建模，利用交互建模得到的交互特征$h_{ij}$作为anchor example。选择相对应的交互评论$e_{ij}$作为正样本，而从整个训练集中随机得到的一个评论$e_{i'j'}$作为负样本，ED的目标是将$h_{ij}$与$e_{ij}$靠近，而与$e_{i'j'}$远离。优化目标公式为：

$$ \mathcal{L}_{2}=-\mathbb{E}_{\mathcal{E}}\left[\log \left(F\left(\boldsymbol{h}_{i j}, \boldsymbol{e}_{i j}\right)\right)\right]+\mathbb{E}_{\mathcal{E} \times \mathcal{E}^{\prime}}\left[\log \left(F\left(\boldsymbol{h}_{i j}, \boldsymbol{e}_{i^{\prime} j^{\prime}}\right)\right)\right] $$

优化：由于RGCL侧重于预测用户对物品的评分，因此采用均方误差（MSE）作为优化目标：

$$ \mathcal{L}_{1}=\frac{1}{|\mathcal{S}|} \sum_{(i, j) \in \mathcal{S}}\left(\hat{r}_{i j}-r_{i j}\right)^{2} $$

$$ \mathcal{L}=\mathcal{L}_{1}+\alpha \mathcal{L}_{2}+\beta \mathcal{L}_{3} . $$

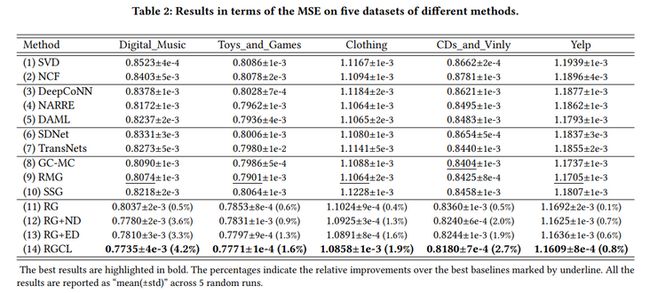
3 实验结果

四、MCCLK

论文标题：Multi-level Cross-view Contrastive Learning for Knowledge-aware Recommender System

论文来源：SIGIR’22

论文链接：https://arxiv.org/abs/2204.08807

代码链接：https://github.com/CCIIPLab/M...

1 MCCLK核心思想

传统的对比学习方法多通过统一的数据增强方式生成两个不同的视图，本文别出心裁，从知识图不同视图的角度去应用对比学习，提出了一种多层次跨视图对比学习机制。

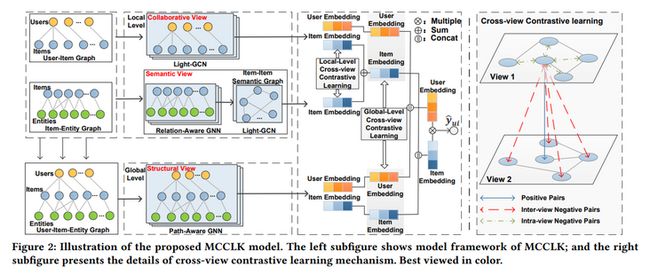
结合了KGR的特点，论文考虑了三种不同的图视图，包括全局结构视图、局部协同视图和语义视图，视图的理解参见下图~

值得一说的是，针对在语义视图，文章提出物品-物品语义图构建模块去获取以往工作中经常忽略的重要物品-物品语义关系。

2 算法细节

从模型图中可以看出，MCCLK包括三个主要部分视图生成、局部对比学习和全局对比学习。

多视图生成：前面我们说道一共需要构建三个视图，这里详细解释一下三个视图究竟是什么。其中全局结构视图为原始的用户-物品-实体图，协同视图与语义视图分别为用户-物品-实体图生成的用户-物品图和物品-实体图。由于全局结构视图与协同视图很常见，所以重点在构建语义视图。

为了考虑物品-物品语义关系，构建带有关系感知聚合机制的 $k$ 阶邻居物品-物品语义图 $S$，可同时保留相邻实体和关系信息。其中 $S_{ij}$表示物品$i$与$j$之间的语义相似度，$S_{ij}=0$表示两个物品之间没有联系。

从知识图$\mathcal{G}$递归学习$K'$次物品表示，提出的关系感知聚合机制为：

$$ \mathbf{e}_{i}^{(k+1)}=\frac{1}{\left|\mathcal{N}_{i}\right|} \sum_{(r, v) \in \mathcal{N}_{i}} \mathbf{e}_{r} \odot \mathbf{e}_{v}^{(k)}\\ \mathbf{e}_{v}^{(k+1)}=\frac{1}{\left|\mathcal{N}_{v}\right|}\left(\sum_{(r, v) \in \mathcal{N}_{v}} \mathbf{e}_{r} \odot \mathbf{e}_{v}^{(k)}+\sum_{(r, i) \in \mathcal{N}_{v}} \mathbf{e}_{r} \odot \mathbf{e}_{i}^{(k)}\right) $$

通过这种方式将KG中的相邻实体和关系编码到物品表示中，并通过余弦相似度构建物品-物品的相似度：

$$ S_{i j}=\frac{\left(\mathbf{e}_{i}^{\left(K^{\prime}\right)}\right)^{\top} \mathbf{e}_{j}^{\left(K^{\prime}\right)}}{\left\|\mathbf{e}_{i}^{\left(K^{\prime}\right)}\right\|\left\|\mathbf{e}_{j}^{\left(K^{\prime}\right) \|}\right\|} $$

在全连接物品-物品图上进行KNN稀疏化，以减少计算需求、可行噪声和不重要边：

$$ \widehat{S}_{i j}=\left\{\begin{array}{ll} S_{i j}, & S_{i j} \in \text { top-k }\left(S_{i}\right) \\ 0, & \text { otherwise } \end{array}\right. $$

局部级对比学习：从模型图可以看出，利用协同视图和语义视图中物品的视图embedding，可以实现局部级的交叉视图对比学习。在这之前，我们先来看两个视图中的编码部分。

1. 协同视图（即，物品-用户-物品）编码，采用Light-GCN递归地执行聚合操作：

$$ \begin{aligned} \mathbf{e}_{u}^{(k+1)} &=\sum_{i \in \mathcal{N}_{u}} \frac{1}{\sqrt{\left|\mathcal{N}_{u}\right||\mathcal{N} i|}} \mathbf{e}_{i}^{(k)} \\ \mathbf{e}_{i}^{(k+1)} &=\sum_{u \in \mathcal{N}_{i}} \frac{1}{\sqrt{\left|\mathcal{N}_{u}\right||\mathcal{N} i|}} \mathbf{e}_{u}^{(k)} \end{aligned} $$

将不同层地表示相加，得到局部协同表示：

$$ \mathrm{z}_{u}^{c}=\mathbf{e}_{u}^{(0)}+\cdots+\mathbf{e}_{u}^{(K)}, \quad \mathbf{z}_{i}^{c}=\mathbf{e}_{i}^{(0)}+\cdots+\mathbf{e}_{i}^{(K)} $$

2. 语义视图，关注物品之间的语义相似度，同样地采用Light-GCN执行聚合操作：

$$ \mathbf{e}_{i}^{(l+1)}=\sum_{j \in \mathcal{N}(i)} \widetilde{S}_{j}^{(l)} $$

将不同层相加，得到局部语义表示：

$$ \mathbf{z}_{i}^{S}=\mathbf{e}_{i}^{(0)}+\cdots+\mathbf{e}_{i}^{(L)} $$

3. 局部级交叉视图对比优化

首先将上述两个视图的embedding送到一个具有隐藏层MLP中：

$$ \begin{array}{l} \mathbf{z}_{i-1}^{c} \mathrm{p}=W^{(2)} \sigma\left(W^{(1)} \mathrm{z}_{i}^{c}+b^{(1)}\right)+b^{(2)} \\ \mathbf{z}_{i-1}^{s} \mathrm{p}=W^{(2)} \sigma\left(W^{(1)} \mathbf{z}_{i}^{s}+b^{(1)}\right)+b^{(2)} \end{array} $$

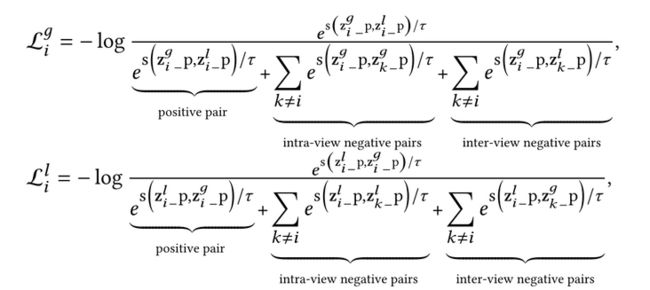
对比损失为：

注意，负样本有两个来源，分别为视图内节点和视图间节点，对应于公式分母中的第二项和第三项。

全局级对比学习：这里设计了一个路径感知GNN（该GNN可以在进行$L'$次聚合的同时保留路径信息，即user-interact-item-relation-entity等远程连接），将路径信息自动编码到节点embedding中，然后利用全局级视图和局部级视图的编码embedding，进行全局级对比学习。

结构视图的聚合公式为：

$$ \begin{aligned} \mathbf{e}_{u}^{(l+1)} &=\frac{1}{\left|\mathcal{N}_{u}\right|} \sum_{i \in \mathcal{N}_{u}} \mathbf{e}_{i}^{(l)}, \\ \mathbf{e}_{i}^{(l+1)} &=\frac{1}{\left|\mathcal{N}_{i}\right|} \sum_{(r, v) \in \mathcal{N}_{i}} \beta(i, r, v) \mathbf{e}_{r} \odot \mathbf{e}_{v}^{(l)}, \end{aligned} $$

其中，注意力权重$\beta(i, r, v)$的计算公式为：

$$ \begin{aligned} \beta(i, r, v) &=\operatorname{softmax}\left(\left(\mathbf{e}_{i} \| \mathbf{e}_{r}\right)^{T} \cdot\left(\mathbf{e}_{v} \| \mathbf{e}_{r}\right)\right) \\ &=\frac{\exp \left(\left(\mathbf{e}_{i} \| \mathbf{e}_{r}\right)^{T} \cdot\left(\mathbf{e}_{v} \| \mathbf{e}_{r}\right)\right)}{\sum_{\left(v^{\prime}, r\right) \in \hat{\mathrm{N}}(i)} \exp \left(\left(\mathbf{e}_{i} \| \mathbf{e}_{r}\right)^{T} \cdot\left(\mathbf{e}_{v^{\prime}} \| \mathbf{e}_{r}\right)\right)}, \end{aligned} $$

将所有层的表示相加，得到全局表示：

$$ \mathbf{z}_{u}^{g}=\mathbf{e}_{u}^{(0)}+\cdots+\mathbf{e}_{u}^{\left(L^{\prime}\right)}, \quad \mathbf{z}_{i}^{g}=\mathbf{e}_{i}^{(0)}+\cdots+\mathbf{e}_{i}^{\left(L^{\prime}\right)} $$

全局级交叉视图对比优化，获取全局级和局部级视图下的节点表示，首先对其映射计算：

$$ \begin{array}{c}\mathrm{z}_{i-}^{g} \mathrm{p}=W^{(2)} \sigma\left(W^{(1)} \mathrm{z}_{i}^{g}+b^{(1)}\right)+b^{(2)} \\\mathrm{z}_{i-}^{l} \mathrm{p}=W^{(2)} \sigma\left(W^{(1)}\left(\mathrm{z}_{i}^{c}+\mathrm{z}_{i}^{s}\right)+b^{(1)}\right)+b^{(2)}\end{array} $$

采用与局部级对比相同的正负采样策略，有以下对比损失：

总体目标如下：

$$ \mathcal{L}^{\text {global }}=\frac{1}{2 N} \sum_{i=1}^{N}\left(\mathcal{L}_{i}^{g}+\mathcal{L}_{i}^{l}\right)+\frac{1}{2 M} \sum_{i=1}^{M}\left(\mathcal{L}_{u}^{g}+\mathcal{L}_{u}^{l}\right) $$

多任务训练

$$ \mathcal{L}_{M C C L K}=\mathcal{L}_{\mathrm{BPR}}+\beta\left(\alpha \mathcal{L}^{\text {local }}+(1-\alpha) \mathcal{L}^{\text {global }}\right)+\lambda\|\Theta\|_{2}^{2}, $$

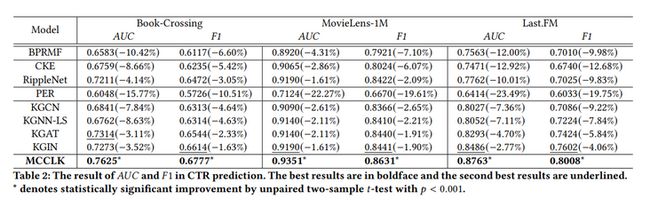
3 实验结果

实验可见，MCCLK在所有度量方面均优于三个数据集的baselines。针对AUC在书籍、电影和音乐数据集，分别提高了3.11%、1.61%和2.77%。

五、MIDGN

论文标题：Multi-view Intent Disentangle Graph Networks for Bundle Recommendation

论文来源：AAAI’22

论文链接：https://arxiv.org/pdf/2202.11...

代码链接：CCIIPLab/MIDGN (github.com)

1 MIDGN核心思想

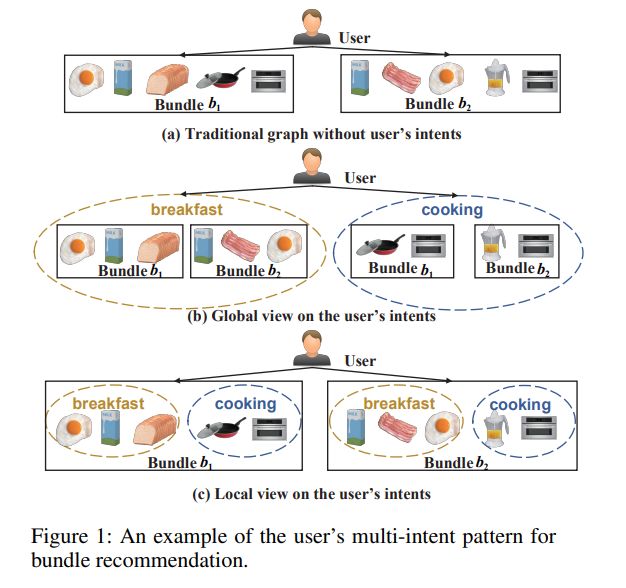
该模型将DGCF的解耦思路用在了bundle推荐，从全局（解耦bundle间的用户意图）和局部（解耦bundle中的用户意图）两个视图对用户意图进行解耦，并采用InfoNCE加强学习效果。下图可以形象地解释上述两个视图~

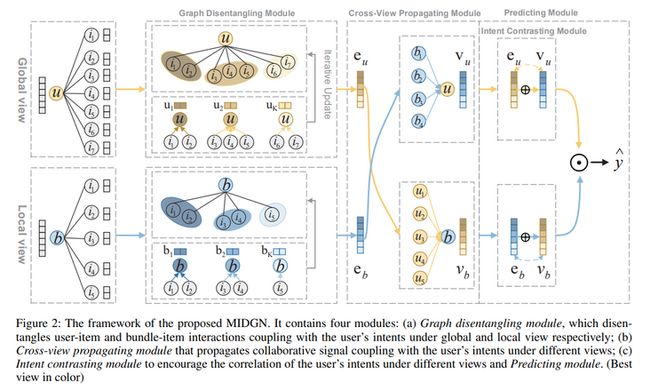
2 算法细节

从图中可以看到，MIDGN由四个不同的模块组成：图解耦模块、 视图交叉传播模块、意图对比模块和预测模块。

图解耦模块

初始化。模型设置$K$个意图，分别对应一组意图感知图$\mathcal{G} = \left\{\mathcal{G}_{1}, \mathcal{G}_{2}, \cdots, \mathcal{G}_{K}\right\}$。由于用户和bundle在不同的意图上应该有不同的embedding，故将其embedding分为$K$块，$\left(\mathbf{u}_{1}, \mathbf{u}_{2}, \cdots, \mathbf{u}_{K}\right), \quad \mathbf{b}=\left(\mathbf{b}_{1}, \mathbf{b}_{2}, \cdots, \mathbf{b}_{K}\right)$块与意图相耦合。由于每一件物品为用户出于某一种意图购买的，不需要对物品进行embedding划分，物品embedding通过随机初始化得到。

为每个意图感知图构建一个加权邻接矩阵$A_k$，其中$A_k(c,i)$表示bundle与物品交互基于第$k$个意图的置信度。

$$ \mathbf{A}(c, i)=\left(\mathbf{A}_{1}(c, i), \mathbf{A}_{2}(c, i), \cdots, \mathbf{A}_{K}(c, i)\right) $$

初始化$\mathbf{A}(c, i)=(1,1, \cdots, 1)$。

意图感知交互图解耦。基于每个意图感知图计算用户和bundle的embedding：

$$ \mathbf{e}_{c k}^{(1)}=g\left(\mathbf{c}_{k},\left\{\mathbf{i}, \mathbf{i} \in \mathcal{N}_{c}\right\}\right) $$

图解耦模块采用邻居路由机制，对图$\mathcal{G}_k$迭代更新用户/bundle的embedding块$c_k^t$和邻接矩阵$A_k^t$。每次迭代使用$c_k^t$和$A_k^t$来记录$c_k$和$A_k$的更新。对于每个交互$(c,i)$，记录其在$K$个意图上的置信度。为了得到分布，对置信度应用softmax：

$$ \tilde{\mathbf{A}}_{k}^{t}(c, i)=\frac{\exp \mathbf{A}_{k}^{t}(c, i)}{\sum_{k^{\prime}=1}^{K} \exp \mathbf{A}_{k^{\prime}}^{t}(c, i)} $$

然后在每个意图感知图进行embedding传播：

$$ \mathbf{c}_{k}^{t}=\sum_{i \in \mathcal{N}_{c}} \frac{\tilde{\mathbf{A}}_{k}^{t}(c, i)}{\sqrt{D_{t}^{k}(c) \cdot D_{t}^{k}(i)}} \cdot \mathbf{i} $$

每个意图下交互的置信度更新公式为：

$$ \mathbf{A}_{k}^{t+1}(c, i)=\mathbf{A}_{k}^{t}(c, i)+\mathbf{c}_{k}^{t^{\mathrm{T}}} \cdot \mathbf{i} $$

embedding的多层组合。模型聚合高阶信息：

$$ \mathbf{e}_{c k}^{l}=g\left(\mathbf{e}_{c k}^{l-1},\left\{\mathbf{i}, \mathbf{i} \in \mathcal{N}_{c}\right\}\right) $$

将来自不同层的意图感知表示求和，得到最终表示：

$$ \mathbf{e}_{c k}=\sum_{l} \mathbf{e}_{c k}^{l} $$

图解耦模块从用户-物品交互图中学习分布在不同bundle(全局视图)中的用户意图；从bundle-物品图中，学习用户在每个bundle(局部视图)中的多个意图。结合来自全局和局部视图的意图，得到用户和bundle的表示：

$$ \begin{array}{l} \mathbf{e}_{u}=\left(\mathbf{e}_{u 1}, \mathbf{e}_{u 2}, \cdots, \mathbf{e}_{u K}\right) \\ \mathbf{e}_{b}=\left(\mathbf{e}_{b 1}, \mathbf{e}_{b 2}, \cdots, \mathbf{e}_{b K}\right) \end{array} $$

视图交叉传播模块：为了在不同的视图下在用户和bundle块之间交流意图，模型在用户-bundle交互图采用了LightGCN：

$$ \begin{aligned} \mathbf{v}_{u} &=\sum_{b \in \mathcal{N}_{u}} \frac{1}{\sqrt{\left|\mathcal{N}_{u}\right|} \sqrt{\left|\mathcal{N}_{b}\right|}} \mathbf{e}_{b}, \\ \mathbf{v}_{b} &=\sum_{u \in \mathcal{N}_{b}} \frac{1}{\sqrt{\left|\mathcal{N}_{b}\right|} \sqrt{\left|\mathcal{N}_{u}\right|}} \mathbf{e}_{u} . \end{aligned} $$

意图对比模块：从不同的角度对比用户和bundle的embedding从而捕获意图：

$$ L_{\text {contrast }}=-\log \left(\frac{\exp \left(\mathbf{e}_{c k} \cdot \mathbf{v}_{c k_{+}}\right)}{\sum_{k^{\prime}} \exp \left(\mathbf{e}_{c k} \cdot \mathbf{v}_{c k^{\prime}}\right)}\right) $$

其中，正样本是不同视图中具有相同意图的块，负样本是其他所有块。

预测和优化

$$ \begin{array}{l} \hat{\mathbf{y}}_{u b}=\left(\mathbf{e}_{u} \oplus \mathbf{v}_{u}\right) \odot\left(\mathbf{e}_{b} \oplus \mathbf{v}_{b}\right)\\ L_{\text {pred }}=\sum_{(u, b, d) \in Q}-\ln \sigma\left(\hat{\mathbf{y}}_{u b}-\hat{\mathbf{y}}_{u d}\right)+\lambda \cdot\|\theta\|^{2} \end{array} $$

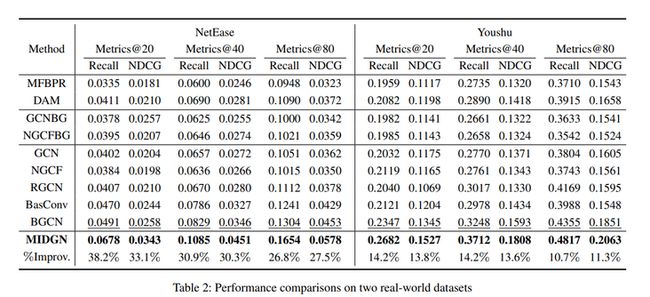
3 实验结果

实验在两个数据集上进行，效果很好，MIDGN在NetEase数据集上将性能提高了26.8%-38.2%，在Youshu上提高了10.7%-14.2%。

总结

五篇文章分别涉及到了协同过滤、序列推荐、基于知识图谱的推荐与bundle推荐，具体应用的技术涉及了EM算法、解耦等。其中第一篇文章NCL和第二篇文章ICL思路较为相近，均采用聚类的思想为节点/序列寻找语义（意图）相似的“邻居”；第三篇文章引入辅助信息（评分和评论）作为边特征改进GNN的图建模，其对比学习的应用也与辅助信息相结合；第四篇文章在KGR中针对不同视图进行了对比任务；第五篇文章则利用解耦的思想为GNN生成多个子图，并利用解耦的子图作为对比任务的视图，思路虽然简单，但效果不错。愿大家读有所思，多发paper。