AI遮天传 ML-集成学习
“Two heads are better than one.”
“三个臭皮匠,顶一个诸葛亮”
把多个人的智慧集合到一起,可能会比一个人好,放在机器学习上,我们借鉴这一经验,把融合多个学习方法的结果来提升效果的方法,我们叫做:Ensemble learning 集成学习。
一、集成学习简介
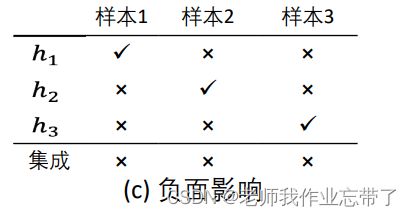
假设我们有三个样本,h1、h2、h3代表三个分类器,预测结果如下:
对于上图这种结果,我们可以看到h1、h2、h3预测的准确率都是2/3,我们让h1、h2、h3进行投票,发现在最后一行,三个样本都预测对了,这样便是产生了积极的影响。
同理对于上面两种情况,分别是没有影响和产生了负面影响。
由于可能会产生不同的影响,因此我们要求:分类器需要效果好且不同!
(效果不好(弱分类器 acc<50%):情况c,相同:情况b)
直觉: 把对同一个问题的多个预测结果综合起来考虑的精度,应该比单一学习方法效果好。
证实: (一些理由)
- 很容易找到非常正确的 “rules of thumb(经验法则)” ,但是很难找到单个的有高准确率的规则
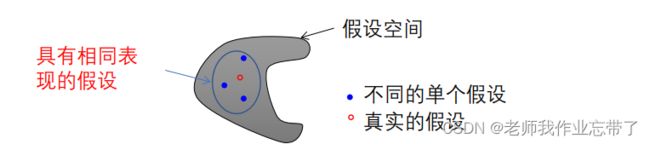
- 如果训练样本很少,假设空间很大,则存在多个同样精度的假设。 选择某一个假设可能在测试集上效果较差。
- 算法可能会收敛到局部最优解。融合不同的假设可以降低收敛到一个不好的局部最优的风险。或者在假设空间中穷举地全局搜索代价太大, 所以我们可以结合一些在局部预测比较准确的假设。
- 由当前算法定义的假设空间不包括真实的假设, 但做了一些不错的近似。
两个概念:
强学习器: 有高准确度的学习算法
弱学习器: 在任何训练集上可以做到比随机预测 略好 error = ½ -γ
我们能否把一个弱学习器增强成一个强学习器?
集成学习基本想法
有时一个单个分类器 (e.g. 决策树、神经网络…) 表现 不好,但是它们的加权融合表现不错。
算法池中的每一个学习器都有它的权重。
当需要对一个新的实例作预测时:
- 每个学习器作出自己的预测
- 然后主算法把这些结果根据权值合并起来,作出最终预测。
集成学习策略
法1:平均
- 简单平均
- 加权平均
法2:投票
- 多数投票法
- 加权投票法
法3:学习
- 加权多数
- 堆叠(Stacking ):层次融合,基学习器的输出作为次学习器的输入。
二、Weighted Majority Algorithm (加权多数算法)
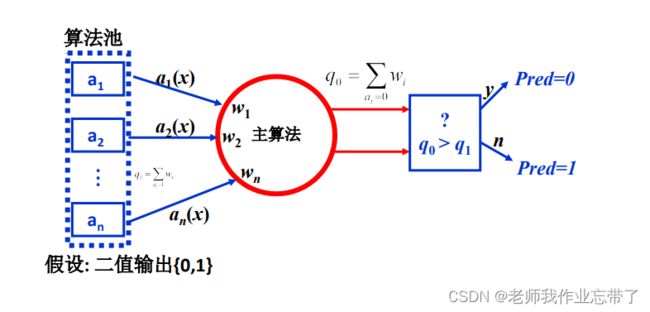
加权多数算法 – 预测
假设二值输出:算法池里有n个算法,每个算法已经有自己的输出,它的权值分别是w1,w2...wn, 主算法对其进行加权得到q0和q1,谁大我们就pred谁。
加权多数算法 – 训练
三、Bagging
如果我们只有一个弱学习器,如何通过集成来提升它的表现?
不同的数据上训练可以获得不同的基础模型
一个朴素的方法: 从训练集种采样不同的子集且训练不同的基础模型
这些模型会大不相同,但它们的效果可能很差。
解决办法: 拔靴采样(Bootstrap sampling)
- 给定集合 D ,含有 m 训练样本;
- 通过从D中均匀随机的有放回采样m个样本构建 Di ;
- 希望 Di 会 遗漏掉 D 中的某些样本。
Bagging 算法
For t = 1, 2, …, T Do
- 从S中拔靴采样产生 Dt
- 在 Dt 上训练一个分类器Ht
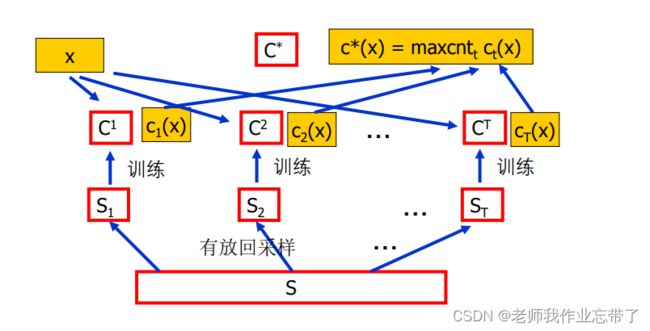
最后,分类一个新的样本x∈X 时,通过对 Ht 多数投票(等权重)。
比如我们从大集合S中放回采样T组,每组样例都有自己的训练值ci,来了一个新的样本x,我们对每个ci(x)进行输出投票。
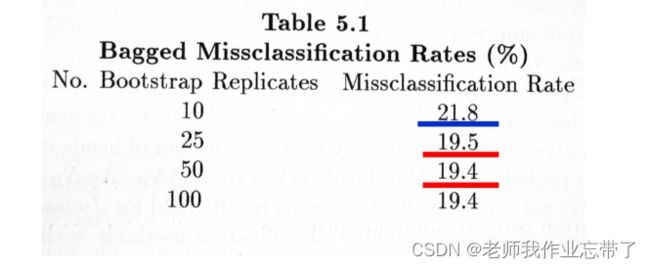
数据集: Rousseeuw 和 Leroy (1986),臭氧含量 vs. 温度。 100 拔靴采样样本。
灰色线条: 初始的10个预测器; 红色线条: 平均。
Breiman “Bagging Predictors” Berkeley Statistics Department TR#421, 1994。
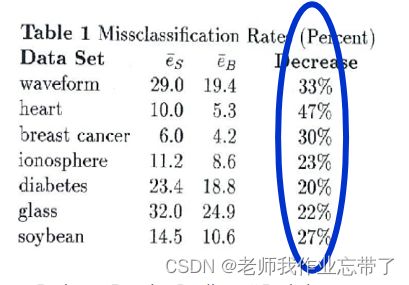
给定样例集S,Breiman重复下列工作100次报告平均结果:
方法 I:
- 把 S 随机划分成测试集 T(10%) 和训练集 D (90%)
- 从D中训练 决策树 算法,记 eS 为它在测 试集 T 上的错误率
方法 II:
重复50次: 生成拔靴采样集合Di , 进行决策树学习,记 eB 为决策树多数投票在测试 集T上的错误率 (集成大小 = 50)
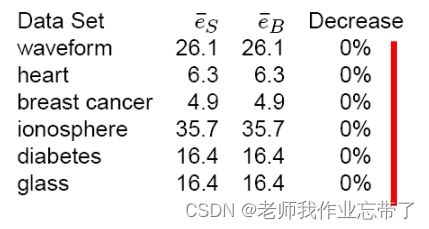
同样的实验,但使用最近邻分类器 (欧式距离)
发生了什么? 为什么 ?
Bagging:讨论
Bagging 在学习器“不稳定”时有用,关键是预测方法的不稳定性。
E.g. 决策树、神经网络
为什么?
- 不稳定: 训练集小的差异可以造成产生的假设大不相同。
- “如果打乱训练集合可以造成产生的预测器大不相同,则bagging算法可以提升其准确率。” (Breiman 1996)
总结
加权多数算法
- 相同数据集, 不同学习算法
- 产生多个模型,加权融合
Bagging
- 一个数据集, 一个弱分类器
- 生成多组训练样本 来训练多个模型,然后集成。
四、Boosting
是否有一个集成算法能够考虑学习中数据的差异性?
基本想法--从失败中学习
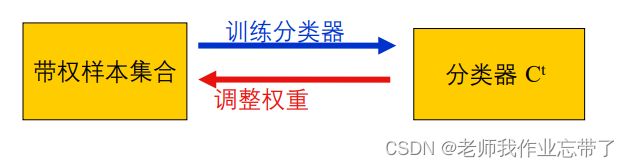
- 给每个样本一个权值
- T 轮迭代,在每轮迭代后增大错误分类样本的权重。 – 更关注于“难”样本
AdaBoost
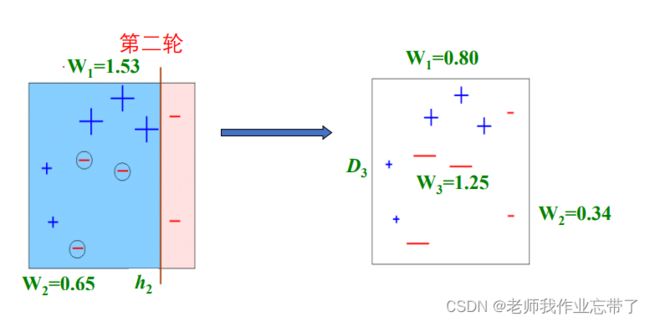
简而言之:少数提升,多数降低。
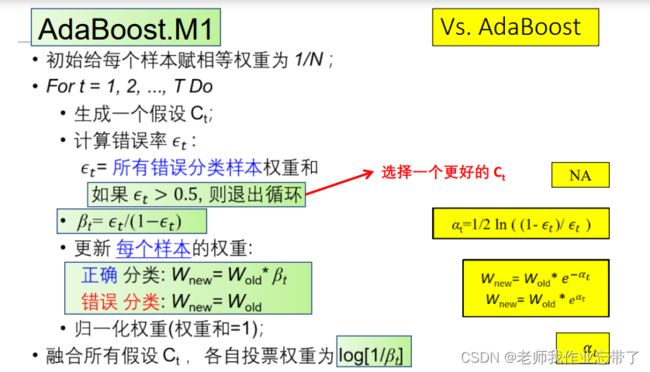
AdaBoost.M1
此时做错的一定是少数派,我们把正确的降低权重(β<1, 归一化),重复t轮融合,去新的权重log(1/β)
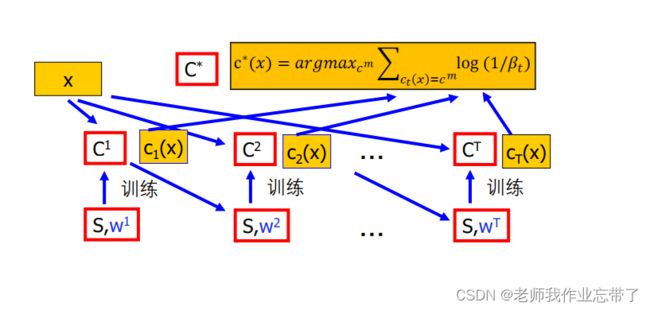
我们不停地更新权重w1,w2...wT,把每一个分类器(带着自己权值)融合在一起,来一个新的样本时加权计算。
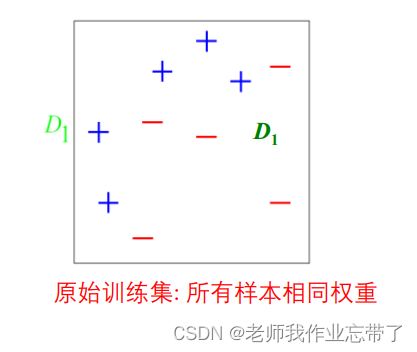
例如:
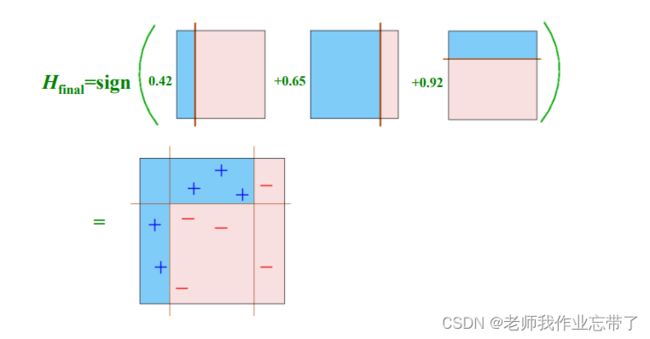
最终假设
AdaBoost在实际使用时的优点
- 快
- 简单 + 易编程实现
- 只有一个参数要调 (T )
- 没有先验知识
- 灵活: 可以和任何分类器结合(NN, C4.5, …)
- 被证明是有效的 (尤其是弱学习器)
- 转变了思路: 现在目标是 仅仅需要寻找比随机猜测好一些的假设就可以了
AdaBoost注意事项
性能依赖于 数据 & 弱学习器
在下列情况中使用AdaBoost会 失效
- 弱学习器 太复杂 (过拟合)
- 弱学习器 太弱 (αt ->0 太快),
- 欠拟合
- 边界太窄->过拟合
过去的实验表明,AdaBoost 似乎 很容易受到噪声的影响
五、讨论
Bagging vs. Boosting
训练集合
- Bagging: 随机选择样本, 各轮训练集相互独立
- Boosting: 与前轮的学习结果有关,各轮训练集并不独立
预测函数
- Bagging: 没有权重; 便于并行
- Boosting: 权重变化 呈指数; 只能顺序进行
效果
- 实际中,bagging几乎总是有效。
- 平均地说,Boosting比bagging好一些,但boosting算法也较常出现损害系统性能的情况。
- 对稳定模型来说bagging效果不好,Boosting可能仍然有效。
- Boosting 可能在有噪声数据上带来性能损失,Bagging没有这 个问题。
重新调权 vs. 重新采样
- Reweighting 调整样本权重可能更难处理
- 一些学习方法无法使用样本权重
- 很多常用工具包不支持训练集上的权重
- Resampling 我们可以重采样来代替:
- 对数据使用boostrap抽样,抽样时根据每个样例的权值确定其被抽样的概率
- 一般重新调权效果会更好一些但重新抽样更容易实现
Bagging & boosting 应用
- 互联网内容过滤
- 图像识别
- 手写识别
- 语音识别
- 文本分类