还不会元学习？看这篇文章

---

---

前言

本文从元学习的介绍， 基于度量的方法，基于网络结构的方法，基于优化的方法记录meta learning的学习过程.来源于李宏毅老师meta learning的three parts， Lilian的博客， 以及与memory work 相关的资料。相关的reference将会放在文章最后。

---

一、元学习的介绍

元学习就是让机器学会学习的技巧， 在学过一些任务之后， 将学习的算法迁移到新的任务中， 经过几步学习就可以产生比较好的模型。

元学习的训练过程，如下图所示。对于一个 training task 来说，输入support set 到F（我们要学习的目标算法）中，F会产生一个f（我们真实需要的一个网络），输入一些query set 到f 会得到输出我们预测/ 分类的结果。

在meta leaning的学习过程中可以参照标准的机器学习的三个步骤：定义一个学习的集合，找到描述学习好坏的方程（loss function），找到方程的最优解

首先， 定我们要学习的算法集合：
对于网络结构， 初始的网络参数， 更新参数的方式（BGD、SGD、MBGD、Momentum、NAG、Adagrad、Adadelta、RMSprop、Adam）来说，都是人为定义的，不同的定义会产生不同的网络结构。但是在metalearning中，我们希望机器自己学会这些内容。

其次，定义一个损失函数。对于每一个task 来说，我们输入support set 的F都会产生一个f。每一个f 对于query set来说都有一个损失函数。将所有的任务的损失进行累加，定义一个L。

最后用梯度下降的方式求最优解。

示例：pandas 是基于NumPy 的一种工具，该工具是为了解决数据分析任务而创建的。

二、元学习的分类

1.基于优化的方法

1.1 LSTM Meta-Learner

https://openreview.net/pdf?id=rJY0-Kcll
https://arxiv.org/abs/1606.04474

LSTM有两个记忆的区域，一个C变化很慢，可以记得比较久的信息。另一个是h随着时间的变化很快。 所以LSTM有长时间的记忆。

把gradient decent当作LSTM来看待，下面的算法有一些参数可以让机器学会，但是这个学习的过程很像RNN的过程。

1.1.1 为什么使用 LSTM？

• 好处
  反向传播中基于梯度的更新跟 LSTM 中 cell 状态的更新有相似之处。
  知道之前的梯度对当前的梯度更新有好处。可以参考 momentum 的原理。

1.1.2 Model Setup

• 压缩模型参数
  如何压缩 LSTM 元学习的参数空间？元学习器是在建模一个神经网络的参数，所以有上百万个变量要学。为了减小元学习器的参数空间，这篇文章借鉴了共享参数的方法。元学习器本质上学习的是一种更新原则，即如何根据一个参数的值和其梯度生成这个参数的新值（比如一阶方法，牛顿法等），与参数在学习器中的位置无关。所以我们可以假设所有参数的更新原则都是一样的，即元学习只需要输出一维变量即可。
  
• List item
  

1.2 MAML

https://arxiv.org/abs/1703.03400
在网络的训练过程中，不同的初始值会对学习过程和最后的学习结果产生很大的影响。
对于MAML来说，只关心学习网络的初始值，经过几个任务的学习之后找到一个最优的初始值φ。当网络迁移到其他任务时，经过几次训练，可以快速的找到最好的初始值。

下图是对于一个train 任务来说，有一个初始值的初始值φ，经过一系列的训练，在这个任务上找到了一个最好的初始值θ^。

但是对于meta leaning 来说，对于一个训练的任务。我们通常使用1 shot learning这样可以让整个训练过程更快。因为训练的数据量比较少，一定程度避免了过拟合的问题。 在test task上我们可以使用support set迭代更多次去训练。

对于所有的train 任务来说，定义一个L，用来更新初始值的初始值。所以整个过程有两次梯度下降的过程。 一次是每一个任务更新得到最好对该任务的初始值θ，第二次是所有的任务加和L更新得到最好的初始值的初始值。

First-Order MAML

数学推导：
First order approximation，由于i！= j 或者i== j的时候需要求解二阶导数，所以假设二阶导数为零。化简方程。

L(φ)对于φ求导相当于l(θ^)对于
θ^求导加和

实际的实现：

1.3 Reptile

https://arxiv.org/abs/1803.02999

1.3.1 The Optimization Assumption

1.3.2 Reptile vs FOMAML

2.基于度量的方法

基于度量的元学习的核心思想类似于最近邻算法(k-NN分类、k-means聚类)和核密度估计。该类方法在已知标签的集合上预测出来的概率，是support set中的样本标签的加权和。 权重由核函数（kernal function） 算得，该权重代表着两个数据样本之间的相似性。

2.1 Convolutional Siamese Neural Network

http://www.cs.toronto.edu/~rsalakhu/papers/oneshot1.pdf

一种更疯狂的想法就是，我们输入一个traning task的support set 和query set到网络中，直接就可以输出结果。

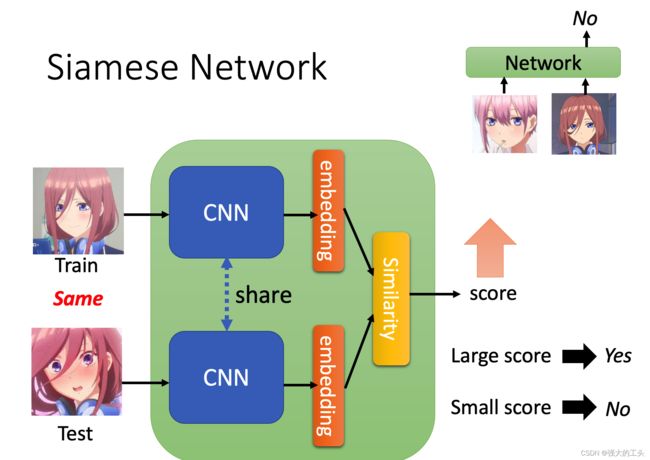
Siamese Neural Network
提出了一种用siamese网络做one-shot image classification的方法。首先，训练一个用于图片验证的siamese网络，分辨两张图片是否属于同一类。然后在测试时，siamese网络把测试输入和support set里面的所有图片进行比较，选择相似度最高的那张图片所属的类作为输出。


我们学到的不同位置的pixel的重要性是不一样的。

首先，卷积siamese网络学习一个由一个CNN网络构成，把两张图片编码为特征向量，两个CNN网络的参数可以共享。如果两个图片差距太大也可以不共享
两个特征向量之间的L1距离可以表示为 |fθ(xi)−fθ(xj)| 。
通过一个linear feedforward layer和sigmoid把距离转换为概率。这就是两张图片属于同一类的概率。loss函数就是cross entropy loss，因为label是二元的。

Training batch B 可以通过对图片做一些变形增加数据量。你也可以把L1距离替换成其他距离，比如L2距离、cosine距离等等。只要距离是可导的就可以。

2.2 Relation Network

https://arxiv.org/abs/1711.06025

对于每一个输入的support data来说都能算出一个embedding的vector，对于输入的query set来说也有一个vector，但是vector之间的相似度是由另一个函数g算出来的。

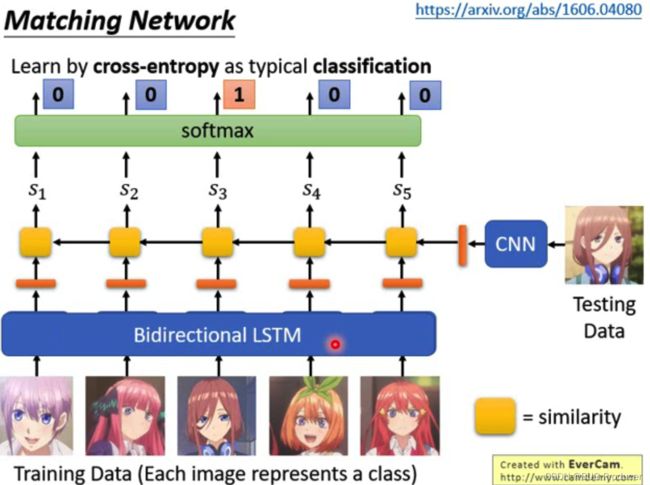
2.3 Prototypical Networks and Matching Networks

https://arxiv.org/abs/1703.05175

• N way one shot learning:
  prototypical Network 就是每一个training data 和 testing data 都计算出一个similarity， 经过soft max 归一化变成概率。

• Few shot learning:
  prototypical Network会把同一类的不同的embedding的值求一个平均值。输入一个testing data，然后看和平均值的哪个值最接近，和K-means类似

• bidirectional LSTM
  本来每个training data的数据都是分开处理的，如果training data的图片互相之间也是有关系的， 所以使用了LSTM的方式去训练。像LSTM、RNN这种模型都要记住一些东西，可是这些样本的类别又不同，所以是想要记住什么？我的理解是将各个类别的样本作为序列输入到LSTM中，是为了模型纵观所有的样本去自动选择合适的特征去度量，例如如果我们的目标是识别人脸，那么就需要构建一个距离函数去强化合适的特征（如发色，脸型等）
  

3.基于网络结构

有两种方式可以实现快速学习，1.设计好模型的内部架构使其能够快速学习，2.用另外一个模型来生成快速学习模型的参数。

3.1 Memory-Augmented Neural Networks

http://proceedings.mlr.press/v48/santoro16.pdf
https://zhuanlan.zhihu.com/p/61037404

许多模型架构使用了外部储存来帮助神经网络学习，像是Neural Turing Machines和Memory Networks。使用外部存储，让神经网络能够更容易的学到新知识并提供给以后使用。这样的模型被称为MANN（”Memory-Augmented Neural Network“）。注意，只使用了内部存储的循环神经网络并不是MANN，比如RNN、LSTM。

3.1.1MANN for Meta-Learning

Santoro et al., 2016提出了一种有意思的训练方式，他们强迫存储器保留当前样本的信息直到对应的标签出现。在每个episode中，标签有 一步的延迟 ，即每次给出的训练对为 ($x_t$,$y_{t-1}$) 。
通过这种设定，MANN会学到要记住新数据集的信息，因为存储器需要保留着当前输入的信息，并且在对应的标签出现的时候取回之前存储的信息进行预测。

https://zhuanlan.zhihu.com/p/100266389

3.1.2 Addressing Mechanism for Meta-Learning

有一个完全基于内容的寻址机制

• 如何取回信息
  read attention 由内容相似度决定。首先，根据t时刻的输入 x ，控制器生成一个键值特征向量 $k_t$ 。然后用类似于NTM的方法，计算键值特征向量和存储器中每个向量的cosine距离，经过softmax归一化，得到一个读取权重向量 $w_r^t$ 。读取向量 $r_t$ 是对存储器中所有向量的加权和：
  $$\sum _{i=1}^N{w}_t^r(i)M_t(i),where:w_t^r=softmax(\frac{k_t\cdot M_t(i)}{||k_t||\cdot ||M_t(i)||})$$
  $M_t$ 是t时刻的存储器矩阵， $M_t(i)$ 是该矩阵中的第i行，即第i个向量。

• 如何往存储器中写入信息?

  最少使用的位置：目的是保存经常使用的那些信息(参见LFU);
  最近使用的位置：原因是刚用过的信息很有可能不会马上用到(参见MRU).

3.2 Meta Networks

https://arxiv.org/abs/1703.00837
针对多任务快速泛化设计的元学习模型

3.2.1 Fast Weights

MetaNet 的快速泛化能力依赖“快参数”，快参数是由一个神经网络产生的，慢参数是梯度下降得到的参数。
在MetaNet中，损失梯度作为元信息，被用于生产学习快参数的模型。慢参数和快参数在神经网络中被结合起来用于预测。快参数是针对任务进行优化产生的参数，使用快参数相当于针对当前的任务进行了优化。

3.2.2 Model Components

• fθ ：一个由 θ 决定的编码函数，发挥着元学习器的作用。负责把原始输入编码为特征向量。类似Siamese Neural Network，我们希望训练这个编码函数使得能够根据其生成的特征向量判断两个输入是否属于同一类（验证任务）。
• gϕ ：一个由 ϕ 决定的基学习器，负责完成真正的学习任务。

MetaNet，给这两个模型额外增加了快参数。因此，我们需要额外两个模型，分别用于生成 f 和 g 的快参数。

• Fw ：一个由 w 决定的LSTM，用于学习嵌入函数 f 的快参数 θ+ 。它把 f 在验证任务上的loss梯度作为输入。
• Gv ：一个由 v 决定的神经网络，根据基学习器 g 的loss梯度学习其快参数 ϕ+ 。在MetaNet中，学习器的loss梯度被视作任务的元信息。
  
  

---

参考

李宏毅老师机器学习：http://speech.ee.ntu.edu.tw/~hylee/ml/2021-spring.html
Lilian博客：https://lilianweng.github.io/lil-log/2018/11/30/meta-learning.html