python实现可视化数独求解器(附代码链接及点点讲解)
写在前面:【学校课程要求】
设计一个数独游戏,能自动生成初盘,也能人工设置初盘,能检测人工设置初盘的合法性;
并编写一个求解数独终盘的算法。
1. 准备工作
找了不少资料,这个可视化感觉挺好看的,但是我写完啦,就没仔细看了(这是讲解?的链接,里面有给 github 的地址):https://blog.csdn.net/u010751000/article/details/109610683
学习数独的算法思想,可以参考 知乎季以安 的分享(用到了唯一侯选数法和关键数删减法,感觉这两种算法就可以解决有唯一解的数独题目了):https://zhuanlan.zhihu.com/p/75974196
本文实现的代码,是基于某项目改编的,遍历的方法参考了另一个写的挺简练的项目(但是我找半天找不到地址了,,这两个代码还在,需要的戳我呀)
使用配置: windows 10,python 3.7,pycharm 2018.2,anaconda 2020.11
2. 基本知识
数独盘面是个 9*9 的棋盘,要求利用给出的部分已知数字,基于逻辑和推理,在空白方格上填入数字 1-9,使其在每一行、每一列和每一九宫格中都出现且只出现一次。
对数独游戏难度的设置包括两种:根据初盘中空白方格的多少认定难度,空白方格越多,难度越大;根据求解数独使用的方法来认定难度,求解数独终盘使用的方法越多,难度越大。
数独的解法有很多,其中回溯递归的方法简单易懂,也较容易实现,能够解决全部有解的数独问题。但玩家在实际求解中很少使用遍历的方法,一般采用“直观法”和“候选数法”这两大类求解思维,它们又各自包括多种不同方法:直观法包括唯一解法、基础摒除法、区块摒除法、唯余解法、矩形摒除法、单元摒除法、余数测试法等;候选数法包括唯一候选数法、隐性唯一候选数法、三链数删减法、隐性三链数删减法、矩形顶点删减法、三链列删减法、关键数删减法等。
3. 实现的功能说明
能够根据难度自动生成初盘,也能够人工设置初盘(在交互界面输入;用 txt 文件导入)。
实现的数独求解器不但可以得到求解结果(左侧),还可以得到具体的求解步骤,也能实现“上一步”与“下一步”的分步查看。
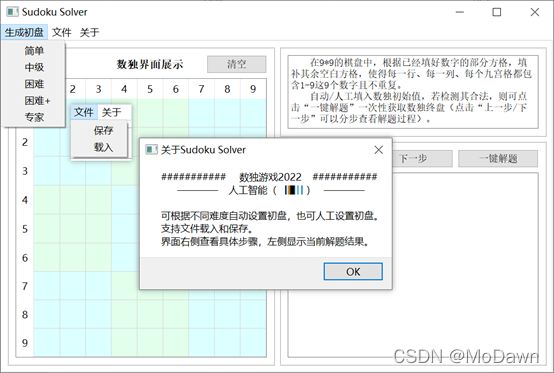
如上图所示,菜单栏分为三部分,点开后如图。点击“生成初盘“,可以进一步选择生成数独题目的难度,包括简单、中级、困难、困难+和专家这五个等级;点击”文件”,可以选择保存或载入,两种方式对应的文件都为.txt文件(包括9行,每行为该行方格对应的字符串);点击“关于”,会弹出中间所示的信息。
主要选项卡包括左侧的数独展示界面(清空按钮可恢复原始状态)、右上的描述信息以及右下的具体步骤展示。
主要功能展示:可根据难度自动生成初盘,也可人工设置初盘(在交互界面输入;用txt文件导入),选择点击右侧的“一键解题”或“上一步”“下一步”来得到最终结果或分步查看。左侧显示求解结果(黑色加粗为初盘数字,橙色为求解得到的数字),右侧显示具体的求解步骤。

根据需要设置了各类提示信息:在载入文件出错时会报错;在当前数据为空时,不能保存为文件或求解数独,否则会出现报错;若人工设置的初盘存在问题,在点击解题后报错。当数独题目可能不止有一个解时(之前使用的方法无法解决),会出现提示,点击“OK”后,会在当前的解题基础上调用回溯遍历法,得到一个可能的解。解题成功时,也会弹出提示信息。
4. 代码实现
本来是作为一个sudoku_solver.py文件的,但是有强迫症,强行理解并拆成了 sudoku_solver.py、show_GUI.py、show_funcion.py,又增加了用于自动生成初盘的sudoku_creator.py(原来是直接读取设置好的数独棋盘)。除此之外,还有两个.txt文件,作为信息显示的读入。下面是讲解以及对应的代码(项目中加了很多注释,以下只是思路的讲解和一小部分代码),全部项目见 gitee:https://gitee.com/mxx11/sudoku
4.1 自动生成数独初盘
这里根据空白方格的数量来划分设置初盘的难度。由于数独的求解过程中涉及到界面展示,生成初盘后无法调用求解过程求解。所以只能保证生成数独初盘一定有解,但不能保证是唯一解(生成后,不再求解验证)。整体可分为以下三步(头两步其实不是很理解,或许生成的基本盘数量比较少,所以需要交换?而且是怎么保证基本盘一定能生成出来的?):
生成基本盘:先生成9*9的棋盘,再从1-9中随机选取第一个方格的数字,然后从左到右,从上到下,遍历生成基本盘,保证1-9在每行、每列、每个九宫格中都出现且只出现一次。
# 生成基本盘
def create_base_sudo(self):
# 9*9的二维矩阵,每个方格默认值为0
sudo = np.zeros((9, 9), dtype=int)
# 随机生成第一个方格的数字
num = random.randrange(9) + 1
# 遍历从左到右,从上到下逐个遍历
for row_index in range(9):
for col_index in range(9):
# 获取该方格对应的行、列、九宫格
sudo_row = sudo[row_index, :] # 获取方格所在的行的全部方格
sudo_col = sudo[:, col_index] # 获取方格所在的列的全部方格
row_start = row_index // 3 * 3 # 获取方格所在的九宫格的全部方格
col_start = col_index // 3 * 3
sudo_block = sudo[row_start: row_start + 3, col_start: col_start + 3]
# 如果该数字已经存在于对应的行/列/九宫格,则继续判断下一个候选数字,直到没有重复
while (num in sudo_row) or (num in sudo_col) or (num in sudo_block):
num = num % 9 + 1
sudo[row_index, col_index] = num # 赋值
num = num % 9 + 1
return sudo
通过随机交换得到终盘:根据观察可以发现,在已有的数独结果上,调换同一个九宫格内任意两个方格所在的行/列后的结果,还是一个有效的数独。据此,多次随机交换行和列,可以得到一个与基本盘相差较大的终盘。
# 随即交换生成终盘
def random_sudo(self):
sudo = self.create_base_sudo()
times = 50 # 交换次数
for _ in range(times):
# 随机交换两行
rand_row_base = random.randrange(3) * 3 # 从0,3,6随机取一个
rand_rows = random.sample(range(3), 2) # 从0,1,2中随机取两个数
row_1 = rand_row_base + rand_rows[0]
row_2 = rand_row_base + rand_rows[1]
sudo[[row_1, row_2], :] = sudo[[row_2, row_1], :]
# 随机交换两列
rand_col_base = random.randrange(3) * 3
rand_cols = random.sample(range(3), 2)
col_1 = rand_col_base + rand_cols[0]
col_2 = rand_col_base + rand_cols[1]
sudo[:, [col_1, col_2]] = sudo[:, [col_2, col_1]]
return(sudo)
根据难度挖去不同数量的方格:实际测试表明,空白方格的数量控制在17-67比较恰当,即最多清除64个数字,最少清除14个数字。据此将难度分为5个等级,每个等级挖去数字的数量区间不同。在挖去数字时,用0-80代指81个方格。随机生成0-80间指定数量的数字,再计算每个随机生成的数字指代方格的所在行和所在列,将其挖去。
# 根据难度等级擦除方格
def get_sudo_subject(self, level):
sudo = self.random_sudo()
subject = sudo.copy()
max_clear_count = 64 # 最多清除个数
min_clear_count = 14 # 最少清除个数
each_level_count = (max_clear_count - min_clear_count) / 5 # 每个等级清除的个数
level_start = min_clear_count + (level - 1) * each_level_count # 该等级最小数
del_nums = random.randrange(level_start, level_start + each_level_count) # 该等级范围内的随机数
# 随机擦除(从0到80,随机取要删除的个数)
clears = random.sample(range(81), del_nums)
for clear_index in clears:
# 把0到80的坐标转化成行和列索引,避免重复删除同一个格子的数字
row_index = clear_index // 9
col_index = clear_index % 9
subject[row_index, col_index] = 0
subject = self.change_format(subject)
return subject
4.2 求解数独终盘
设置求解数独终盘的整体过程:
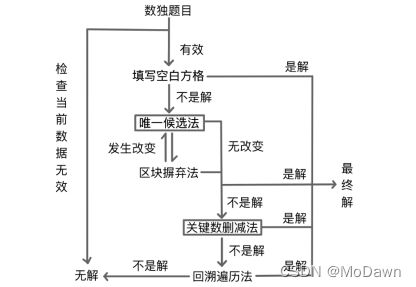
如下图所示,先根据规则要求,得到每个方格的可能取值,再循环使用唯一候选数法和区块摒除法。若仍未解决,则进一步使用关键数删减法,若尝试10个有多个可能值的方格后,仍未得到最终解,判定方法失败,使用回溯遍历法得到一个可能解。图中画框的方法用到了全局更新,会在后面详细说明。
def solve_sudoku(self):
if self.check_data_validation(): # 检查原始数据是否有效
self.update_step_list(['#############################',
'在空白方格中填充所有可能数字',
'#############################'])
if not self.fill_blank_cell(): # 在空白方格中填充所有可能数字
return False
if self.check_sudoku_result(): # 数独解决:返回
return True
else:
if self.basic_methods_loop(): # 唯一候选法和区块摒弃法
return True
else:
array_now = self.sudoku_data_dic['row'] # 存储关键数删减法尝试前的数独题目
if self.key_number_reduction_method():
return True
else: # 最终尝试回溯遍历法(使用array_now)
if self.back_find_a_solution(array_now): # 数独解决:返回
return True
else: # 数独无法解决:返回错误信息
self.update_step_list(['', '抱歉,解题失败!无法找到最终解!'],
['抱歉,解题失败!无法找到最终解!'])
设置了几个用到的基础函数:
用于检查原始数据是否有效、是否得到最终解;
用于填写空白方格的可能取值、获取新的数独题目。这里填写空白方格的可能取值挺有意思,不是找行/列/九宫格值域的交集,而是遍历1-9,看是否在行/列/九宫格中出现,这与它设置的信息交互方式有关。
循环使用唯一候选数法和区块摒除法:
先调用唯一候选法,若未发生改变则返回False;若发生改变且为最终结果,则返回True;若发生改变且不是最终结果,则调用区块摒弃法。
若未发生改变则返回False;若发生改变且为最终结果,则返回True;若发生改变且不是最终结果,则循环,再次调用唯一候选法。
def basic_methods_loop(self):
while True:
self.get_sudoku_table_data() # 保存唯一候选数法前数独数据
unique_data_dic = self.sudoku_data_dic['row']
if not self.unique_candidate_method(): # 唯一候选数法
return False
self.get_sudoku_table_data() # 对比是否发生改变
if unique_data_dic == self.sudoku_data_dic['row']:
return False
if self.check_sudoku_result(): # 改变且已为最终结果
return True
else: # 如果发生改变:调用区块摒弃法
self.get_sudoku_table_data() # 保存区块摒弃法前数独数据
block_data_dic = self.sudoku_data_dic['row']
self.block_exclusion_method() # 区块摒弃法
self.get_sudoku_table_data() # 对比是否发生改变
if block_data_dic == self.sudoku_data_dic['row']:
return False
if self.check_sudoku_result(): # 改变且已为最终结果
return True
唯一候选数法:
逐渐排除不合适的候选数,当某个方格的候选数排除至只有一个数字时,这个数字为该方格的唯一候选数,即最终解。排除方法:若在某行/列/九宫格中,只有某个方格的可能值含有某数字,那么该方格的值可以唯一确定为该数字。实现时,对每行/列/九宫格中各方格的值域分别进行不去重合并,若原方格的某个可能取值在合并得到的新列表中唯一,则将这个唯一值赋值给该值所在方格。
这个方法会进行多轮,涉及多次全局更新:分别寻找每行、每列、每个九宫格的中仅出现一次的数字,若有这样的数字,则将其所在方格的值替换为该数字,然后由当前有确定值的方格得到新的数独题目,再在空白方格中填入可能值,并再次寻找每行、每列、每个九宫格的中仅出现一次的数字。循环以上步骤直至不再发生改变。
区块摒除法:
在九宫格中,如果某一数字仅出现在某行或某列中,那么这一行或者这一列中,其它九宫格的可能取值都可以排除掉这个数字。可以通过构建词典来实现。词典格式:{1: {‘row’: [2, 4], ‘column’: [3]}}
实际上也可以多轮,但感觉性价比不高(实际上这个方法一般情况下也没多大用?);也不涉及全局更新,若有改变,会直接再调用唯一候选数法,在唯一候选数法中更新即可。
关键数删减法:
对某个有多个可能取值的方格,依次假定每个可能取值为该方格的最终结果,继续求解。如果发生错误,则尝试其他可能取值。
具体实现:依次尝试未确定方格的所有可能值,并将其填入方格,然后据此得到新的数独题目,再在空白方格中填入可能值。若出现错误,则尝试数字不合理;若未出现错误,则调用唯一候选数法和区块摒弃法,检验新得到的数独是否有解(有解则返回True,无解则尝试下一个可能值)。若当前未确定方格的所有可能值都没有解,则恢复尝试前数据,开始尝试下一个未确定方格的所有可能值。
根据观察,在尝试10个未确定方格后仍没有解时,应终止尝试,节省时间。
本来的想法是不断使用递归:依次尝试未确定方格的所有可能值,递归检测所选值是否正确。在假设某方格的值后,检查得到的值域列表是否合法。若值域列表合法,进一步检验是否已得到最终答案,若仍不是最终答案,则调用递归,查看下一个可能数字不唯一的方格,直至调用过程中返回最终解或最终发现无唯一解;若值域列表不合法,则更换当前尝试方格的选值,若所有选值得到的值域列表均不合法,则数独题目无唯一解。
但是在实际编写时才发现,由于最初的设定是每步都可以显示,所以递归难以实现,最终思路为:依次尝试未确定方格的所有可能值,检验新得到数独是否有解;若都没有解,则尝试下一个未确定方格的所有可能值。
回溯遍历法:
考虑到自动设置的初盘可能不止有唯一解,而之前的方法只能求解有唯一解的数独题目。所以在使用以上方法尝试失败后,又设置了回溯遍历法,能够得到数独题目的一个可能解。实现时,依次尝试每个未确定方格的值,可行则继续尝试下一个方格,有误则不断回溯,再次尝试。由于涉及递归,此方法只展示右侧的具体步骤以及最终结果,不支持“上一步”和“下一步”操作。
具体实现:在调用关键数删减法前,保存当时的数独题目,若关键数删减法尝试失败,则将尝试前的数独题目传入回溯遍历法。在回溯遍历函数中设置列表spaces存储不确定方格的位置;设置新的行、列、九宫格列表,用于存储1-9中每个数字是否在该行、列、九宫格中出现。最初将有确定值方格对应的位置设为True,其余设为False。然后开始递归,将当前确定方格对应的位置设为True,失败则回溯并将尝试失败的对应位置改回False。通过设置True和False值来完成回溯遍历。
4.3 求解与可视化间的数据信息连接
表格中的数据存储在sudoku_data_dic中,便于直接获取行、列、九宫格形式的列表。相当于列、九宫格形式的数据与行形式数据的转换,感觉很巧妙。
def get_sudoku_table_data(self):
self.sudoku_data_dic = {
'row': [['' for i in range(9)] for j in range(9)],
'column': [['' for i in range(9)] for j in range(9)],
'block': [[] for j in range(9)]
}
for row in range(9):
for column in range(9):
cell_value = self.sudoku_table.item(row, column).text().strip()
self.sudoku_data_dic['row'][row][column] = cell_value
self.sudoku_data_dic['column'][column][row] = cell_value
block_num = (row // 3) * 3 + column // 3 # 所在九宫格
self.sudoku_data_dic['block'][block_num].append(cell_value)
文本展示等用到的信息,存储在step_dic中,并随着解题过程不断添加到step_list中。后续会利用step_list中存储的信息,进行GUI中数独展示界面、步骤展示文本、提示信息的更新与展示。
def update_step_list(self, step_text_list=[], message_text_list=[]):
self.get_sudoku_table_data()
step_dic = {
'row_list': copy.deepcopy(self.sudoku_data_dic['row']),
'step_text': copy.deepcopy(step_text_list),
'message_text': copy.deepcopy(message_text_list)
}
self.step_list.append(step_dic)
4.4 可视化界面及辅助功能
使用了pyqt5,用于绘制交互界面,主要分为菜单栏和主要选项卡。
def init_ui(self):
self.gen_menu_bar() # 生成菜单栏
self.gen_main_tab() # 生成主要选项卡
# 绘制GUI窗口
self.setWindowTitle('Sudoku Solver') # 设置窗口标题
self.resize(1030, 650) # 设置屏幕大小
qr = self.frameGeometry() # 设置在屏幕中间显示
cp = QDesktopWidget().availableGeometry().center()
qr.moveCenter(cp)
self.move(qr.topLeft())
菜单栏 包括3部分:自动生成初盘、文件载入导出、关于。
主要选项卡 包括3部分:数独界面(标题、清空按钮、9*9表格)、描述信息、步骤展示(一键解题、上一步、下一步、文本展示)。
对应的功能也在这里实现,比如文件的载入、保存,清空数独界面;还引用了前面的.py文件,如根据难度自动生成初盘,“上一步” “下一步”。