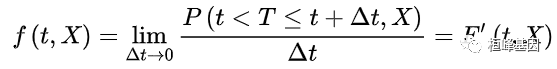Topic 7. 临床预测模型--Cox回归
上期讨论完两种建模方式,这期讲一下经典的 Cox 回归,这个估计大家早就很熟悉了,但是这里还是需要梳理一下到底该怎么使用。
01 Cox回归概念
———————
在介绍Cox回归模型之前,先介绍几个有关生存相关的概念。
1.生存函数具有变量![]() 的观察对象的生存时间 T 大于某时刻 t 的概率,
的观察对象的生存时间 T 大于某时刻 t 的概率,
称为生存函数。生存函数 S(t,X) 又称为累积生存率。
2. 死亡函数具有变量 X 的观察对象的生存时间 T 不大于某时刻 t 的概率,
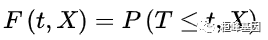
称为死亡函数。死亡函数 F(t,X) 的实际意义是当观察随访到 t 时刻的累积死亡率。
3. 死亡密度函数具有变量X的观察对象在某时刻 t 的瞬时死亡率,称为死亡密度函数。
4. 危险率(风险)函数具有变量 X,且生存时间已达到 X 的观察对象在时刻 t 的瞬时死亡率,
危险率函数 h(t,X) 实际上是一个条件瞬间死亡率 。
- COX回归模型
Cox 回归模型,又称“比例风险回归模型(proportional hazards model,简称Cox模型)”,是由英国统计学家 D.R.Cox(1972) 年提出的一种半参数回归模型。该模型以生存结局和生存时间为因变量,可同时分析众多因素对生存期的影响,能分析带有截尾生存时间的资料,且不要求估计资料的生存分布类型。由于上述优良性质,该模型自问世以来,在医学随访研究中得到广泛的应用,是迄今生存分析中应用最多的多因素分析方法。
- 临床研究需求
在临床研究中,存在许多情况,其中几个已知量(称为协变量)可能影响患者预后。例如,假设比较两组患者:那些患者和没有特定基因型的患者。如果其中一组也包含较老的个体,则存活率的任何差异可归因于基因型或年龄或两者。因此,在研究与任何一个因素相关的生存时,通常需要调整其他因素的影响。
Cox 比例风险模型是用于对生存分析数据建模的最重要方法之一。该模型的目的是同时评估几个因素对生存的影响。换句话说,它允许我们检查特定因素如何影响特定时间点发生的特定事件(例如,感染,死亡)的发生率。该比率通常称为危险率。预测变量(或因子)通常在生存分析文献中称为协变量。风险比(HR)大于1表示与事件概率正相关的协变量,因此与生存期长度负相关。
-
HR=1:无效;
-
HR<1:减少危害 ;
-
HR>1:危险增加。
02 实例分析
——————****
Cox 实例分析我们使用 GBSG2 研究观察结果的数据集,包括实例临床数据,这个数据框包含了乳腺癌患者 686 名女性的观察结果来自一篇1999年发表的文章,这种回归算法也是有定年龄了,而这些数据的说明通过 ?GBSG2 即可获得,包含如下信息:
-
horTh:是否接受激素治疗;
-
age:年龄
-
menostat:绝经状态(两个水平上的一个因素绝经前(绝经前)和绝经后(绝经后));
-
tsize:肿瘤大小;
-
tgrade:肿瘤分级,I < II < III级为有序因子;
-
pnodes:结节数量;
-
progrec:黄体酮受体(fmol);
-
estrec:雌激素受体(fmol);
-
time:时间;
-
cens:截尾指示器(0-截尾,1-事件)。
?GBSG2
Format
This data frame contains the observations of 686 women:
horTh
hormonal therapy, a factor at two levels no and yes.
age
of the patients in years.
menostat
menopausal status, a factor at two levels pre (premenopausal) and post (postmenopausal).
tsize
tumor size (in mm).
tgrade
tumor grade, a ordered factor at levels I < II < III.
pnodes
number of positive nodes.
progrec
progesterone receptor (in fmol).
estrec
estrogen receptor (in fmol).
time
recurrence free survival time (in days).
cens
censoring indicator (0- censored, 1- event).
Source
W. Sauerbrei and P. Royston (1999). Building multivariable prognostic and diagnostic models: transformation of the predictors by using fractional polynomials. Journal of the Royal Statistics Society Series A, Volume 162(1), 71–94.
对文件数据情况进行分析,并查看每列数据的属性,因子变量三个,其他为整数值型变量,如下:
#install.packages("TH.data")
data('GBSG2')
head(GBSG2)
horTh age menostat tsize tgrade pnodes progrec estrec time cens
1 no 70 Post 21 II 3 48 66 1814 1
2 yes 56 Post 12 II 7 61 77 2018 1
3 yes 58 Post 35 II 9 52 271 712 1
4 yes 59 Post 17 II 4 60 29 1807 1
5 no 73 Post 35 II 1 26 65 772 1
6 no 32 Pre 57 III 24 0 13 448 1
str(GBSG2)
'data.frame': 686 obs. of 10 variables:
$ horTh : Factor w/ 2 levels "no","yes": 1 2 2 2 1 1 2 1 1 1 ...
$ age : int 70 56 58 59 73 32 59 65 80 66 ...
$ menostat: Factor w/ 2 levels "Pre","Post": 2 2 2 2 2 1 2 2 2 2 ...
$ tsize : int 21 12 35 17 35 57 8 16 39 18 ...
$ tgrade : Ord.factor w/ 3 levels "I"<"II"<"III": 2 2 2 2 2 3 2 2 2 2 ...
$ pnodes : int 3 7 9 4 1 24 2 1 30 7 ...
$ progrec : int 48 61 52 60 26 0 181 192 0 0 ...
$ estrec : int 66 77 271 29 65 13 0 25 59 3 ...
$ time : int 1814 2018 712 1807 772 448 2172 2161 471 2014 ...
$ cens : int 1 1 1 1 1 1 0 0 1 0 ...
summary(GBSG2)
horTh age menostat tsize tgrade pnodes
no :440 Min. :21.00 Pre :290 Min. : 3.00 I : 81 Min. : 1.00
yes:246 1st Qu.:46.00 Post:396 1st Qu.: 20.00 II :444 1st Qu.: 1.00
Median :53.00 Median : 25.00 III:161 Median : 3.00
Mean :53.05 Mean : 29.33 Mean : 5.01
3rd Qu.:61.00 3rd Qu.: 35.00 3rd Qu.: 7.00
Max. :80.00 Max. :120.00 Max. :51.00
progrec estrec time cens
Min. : 0.0 Min. : 0.00 Min. : 8.0 Min. :0.0000
1st Qu.: 7.0 1st Qu.: 8.00 1st Qu.: 567.8 1st Qu.:0.0000
Median : 32.5 Median : 36.00 Median :1084.0 Median :0.0000
Mean : 110.0 Mean : 96.25 Mean :1124.5 Mean :0.4359
3rd Qu.: 131.8 3rd Qu.: 114.00 3rd Qu.:1684.8 3rd Qu.:1.0000
Max. :2380.0 Max. :1144.00 Max. :2659.0 Max. :1.0000
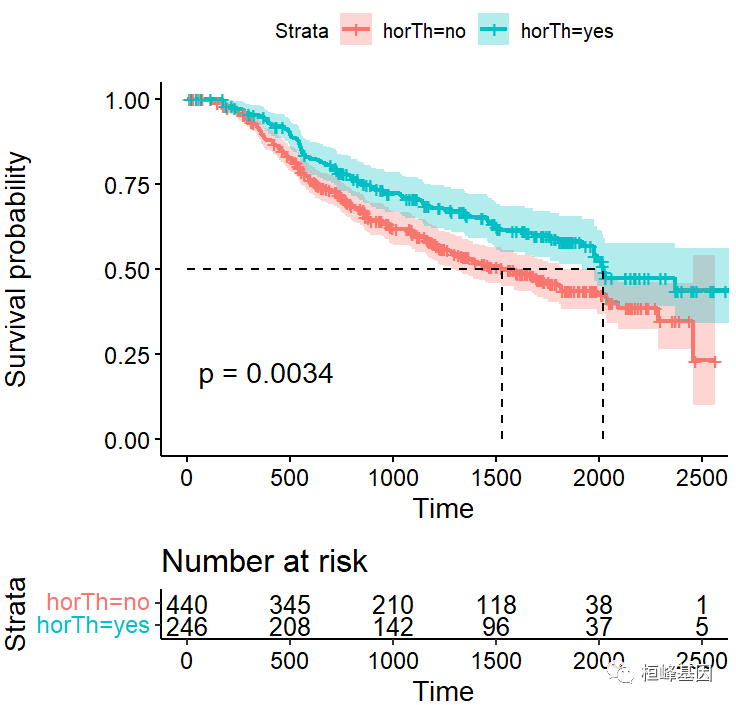
乳腺癌患者是否接受激素治疗对生存期的影响因素,先对是否接受激素治疗进行生存分析即 Kaplan-Meier,结果 P=0.0034, 接受激素治疗的中位时间明显高于未接受激素治疗的患者,如下:
fit=survfit(Surv(time, cens)~horTh,data = GBSG2)
fit
Call: survfit(formula = Surv(time, cens) ~ horTh, data = GBSG2)
n events median 0.95LCL 0.95UCL
horTh=no 440 205 1528 1296 1814
horTh=yes 246 94 2018 1918 NA
ggsurvplot(fit, # 创建的拟合对象
data = GBSG2, # 指定变量数据来源
conf.int = TRUE, # 显示置信区间
pval = TRUE, # 添加P值
risk.table = TRUE, # 绘制累计风险曲线
surv.median.line = "hv", # 添加中位生存时间线
add.all = FALSE, # 添加总患者生存曲线
palette = "hue") # 自定义调色板
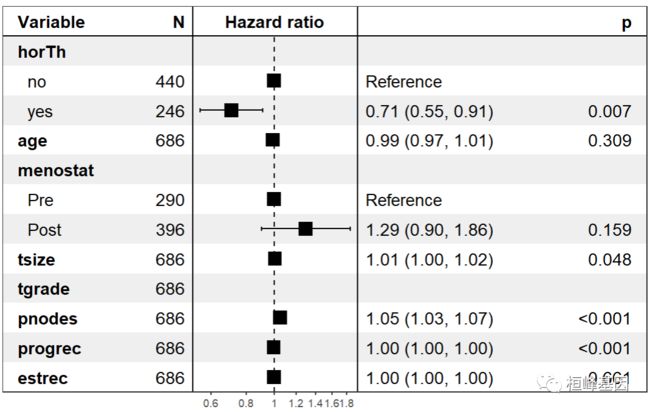
我们继续看还有哪些因素会影响生存期,利用上述结果做 Cox 模型并做森林图,"." 表示所有的变量,p=< 2.2e-16 表示模型显著,如下:
cox <- coxph(Surv(time,cens)~.,data = GBSG2)
summary(cox)
Call:
coxph(formula = Surv(time, cens) ~ ., data = GBSG2)
n= 686, number of events= 299
coef exp(coef) se(coef) z Pr(>|z|)
horThyes -0.3462784 0.7073155 0.1290747 -2.683 0.007301 **
age -0.0094592 0.9905854 0.0093006 -1.017 0.309126
menostatPost 0.2584448 1.2949147 0.1834765 1.409 0.158954
tsize 0.0077961 1.0078266 0.0039390 1.979 0.047794 *
tgrade.L 0.5512988 1.7355056 0.1898441 2.904 0.003685 **
tgrade.Q -0.2010905 0.8178384 0.1219654 -1.649 0.099199 .
pnodes 0.0487886 1.0499984 0.0074471 6.551 5.7e-11 ***
progrec -0.0022172 0.9977852 0.0005735 -3.866 0.000111 ***
estrec 0.0001973 1.0001973 0.0004504 0.438 0.661307
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
exp(coef) exp(-coef) lower .95 upper .95
horThyes 0.7073 1.4138 0.5492 0.9109
age 0.9906 1.0095 0.9727 1.0088
menostatPost 1.2949 0.7723 0.9038 1.8553
tsize 1.0078 0.9922 1.0001 1.0156
tgrade.L 1.7355 0.5762 1.1963 2.5178
tgrade.Q 0.8178 1.2227 0.6439 1.0387
pnodes 1.0500 0.9524 1.0348 1.0654
progrec 0.9978 1.0022 0.9967 0.9989
estrec 1.0002 0.9998 0.9993 1.0011
Concordance= 0.692 (se = 0.015 )
Likelihood ratio test= 104.8 on 9 df, p=<2e-16
Wald test = 114.8 on 9 df, p=<2e-16
Score (logrank) test = 120.7 on 9 df, p=<2e-16
> cox
Call:
coxph(formula = Surv(time, cens) ~ ., data = GBSG2)
coef exp(coef) se(coef) z p
horThyes -0.3462784 0.7073155 0.1290747 -2.683 0.007301
age -0.0094592 0.9905854 0.0093006 -1.017 0.309126
menostatPost 0.2584448 1.2949147 0.1834765 1.409 0.158954
tsize 0.0077961 1.0078266 0.0039390 1.979 0.047794
tgrade.L 0.5512988 1.7355056 0.1898441 2.904 0.003685
tgrade.Q -0.2010905 0.8178384 0.1219654 -1.649 0.099199
pnodes 0.0487886 1.0499984 0.0074471 6.551 5.7e-11
progrec -0.0022172 0.9977852 0.0005735 -3.866 0.000111
estrec 0.0001973 1.0001973 0.0004504 0.438 0.661307
Likelihood ratio test=104.8 on 9 df, p=< 2.2e-16
n= 686, number of events= 299
library(forestmodel)
forest_model(cox,
theme = theme_forest(),
factor_separate_line=TRUE
)
03 结果解读
———
1、coef是公式中的回归系数b(有时也叫做beta值),因此exp(coef)则是Cox模型中最主要的概念风险比(HR-hazard ratio):
-
HR = 1: No effect
-
HR < 1: Reduction in the hazard
-
HR > 1: Increase in Hazard
在癌症研究中:
-
hazard ratio > 1 is called bad prognostic factor
-
hazard ratio < 1 is called good prognostic factor
2、z值代表Wald统计量,其值等于回归系数coef除以其标准误se(coef),即z = coef/se(coef);有统计量必有其对应的假设检验的显著性P值,其说明bata值是否与0有统计学意义上的显著差别;
3、coef(-0.5310)值小于0说明HR值小于1,而这里的Cox模型是group two相对于group one而言的,那么按照测试数据集来说:male=1,female=1,即女性的死亡风险相比男性要低;
4、exp(coef)等于0.59,即风险比例等于0.59,说明女性(male=2)减少了0.59倍风险,女性与良好预后相关;
5、ower .95 upper .95则是exp(coef)的95%置信区间;
6、Likelihood ratio test,Wald test,Score (logrank) test则是给出了3种可选择的P值,这三者是asymptotically equivalent;当样本数目足够大时,这三者的值是相似的;当样本数目较少时,这三者是有差别的,但是Likelihood ratio test会比其他两种在小样本中表现的更优。
04 估计回归关系
——————
根据Cox回归建模,找到了显著预后因子有四个,那么四个预后因子之间又是怎么样的关系?
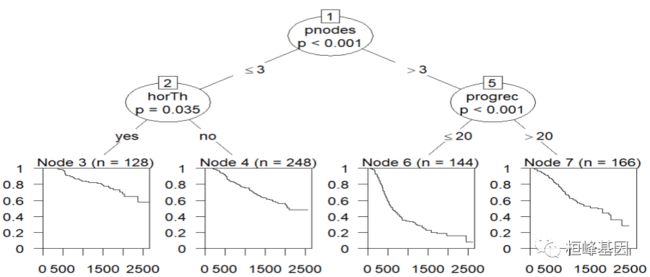
这就涉及到一个条件递归树的概念,条件推理框架下连续、截尾、有序、标称和多元响应变量的递归划分。在条件推理框架中,条件推理树通过二分递归划分来估计回归关系。该算法的工作原理大致如下:
-
检验任意输入变量与响应(也可以是多变量)之间的全局零假设是否独立。如果这个假设不能被否定,就停止。否则,选择与共振关联最强的输入变量。这种关联是由一个p值测量对应于一个单一输入变量和响应的偏零假设的测试;
-
在选定的输入变量中实现二进制分割;
-
递归地重复步骤1和2。
利用上述方法来分析四个显著性因子之间的关系,我觉得这个特别有意义,可以观察到每个因子对影响生存的显著性,以及条件递归树的绘制,其显著因子包括如下:
-
horTh:是否接受激素治疗;
-
pnodes:结节数量;
-
progrec:黄体酮受体(fmol);
-
estrec:雌激素受体(fmol);
#install.packages("party")
library(party)
tree <- ctree(Surv(time,cens)~.,data = GBSG2)
plot(tree)
在研究Cox回归模型的时候突然发现还有这种条件递归树的方法,可以更好的揭示临床上的问题,这期还是收获满满的,有学到了新东西,关注公众号,与我一起来学习吧!
Reference:
-
Helmut Strasser and Christian Weber (1999). On the asymptotic theory of permutation statistics. Mathematical Methods of Statistics, 8, 220–250.
-
Torsten Hothorn, Kurt Hornik, Mark A. van de Wiel and Achim Zeileis (2006). A Lego System for Conditional Inference. The American Statistician, 60(3), 257–263.
-
Torsten Hothorn, Kurt Hornik and Achim Zeileis (2006). Unbiased Recursive Partitioning: A Conditional Inference Framework. Journal of Computational and Graphical Statistics, 15(3), 651–674.
-
Carolin Strobl, James Malley and Gerhard Tutz (2009). An Introduction to Recursive Partitioning: Rationale, Application, and Characteristics of Classification and Regression Trees, Bagging, and Random forests. Psychological Methods, 14(4), 323–348.
-
W. Sauerbrei and P. Royston (1999). Building multivariable prognostic and diagnostic models: transformation of the predictors by using fractional polynomials. Journal of the Royal Statistics Society Series A, Volume 162(1), 71–94.
-
M. Schumacher, G. Basert, H. Bojar, K. Huebner, M. Olschewski, W. Sauerbrei, C. Schmoor, C. Beyerle, R.L.A. Neumann and H.F. Rauschecker for the German Breast Cancer Study Group (1994), Randomized 2\times2 trial evaluating hormonal treatment and the duration of chemotherapy in node-positive breast cancer patients. Journal of Clinical Oncology, 12, 2086–2093.
-
绕绍奇主编;徐天和总主编.中华医学统计百科全书 遗传统计分册:中国统计出版社,2013.05
桓峰基因
生物信息分析,SCI文章撰写及生物信息基础知识学习:R语言学习,perl基础编程,linux系统命令,Python遇见更好的你
28篇原创内容
公众号