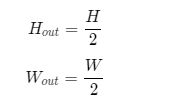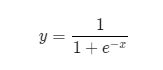飞桨PaddlePaddle-百度架构师手把手带你零基础实践深度学习——21日学习总结
飞桨PaddlePaddle-百度架构师手把手带你零基础实践深度学习——21日学习总结
写在前面的话
纯新手小白，第一次接触深度学习方面的应用。感谢飞桨提供的这次学习机会。之前有学习到深度学习的理论方面的知识，但是到实践，总觉得无从下手，一筹莫展。刚好被朋友推荐一起学习该门课程，感觉受益匪浅。一个好的入门老师可以带来无限的可能。感谢平台提供的机会，感谢几位老师的教导和经验分享。
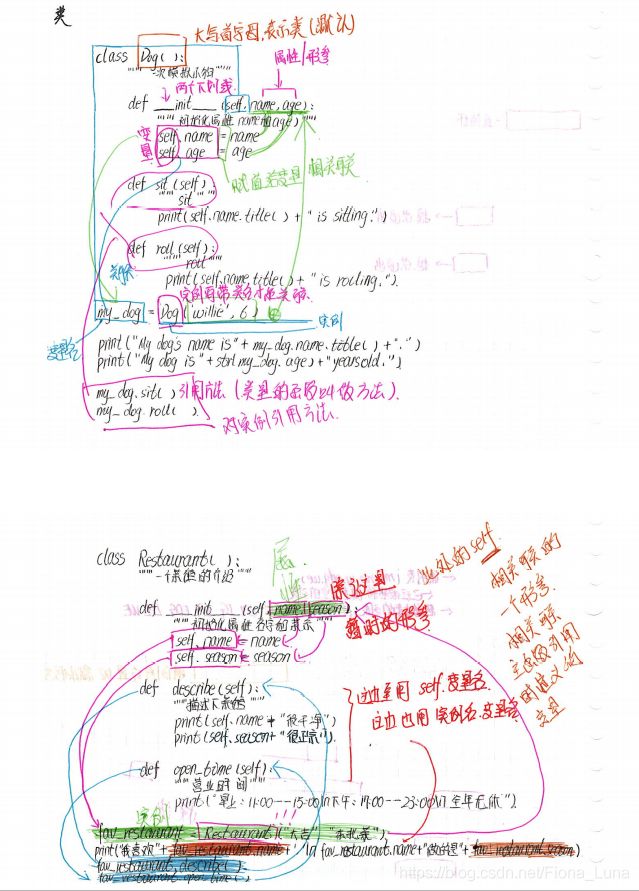
PS：本人自己更喜欢纸质的笔记，所以可能会上传大量图片。
第一章 Python基础
python作为一种“神奇的”编程语言，有着丰富的【办法】和【函数】，它更像是一种工具，简单快捷（尽管我深爱C++）。我习惯把它的基础语言分为以下五种，即：print语句，列表（含元组）字典，循环判断，函数&类， 文件操作。
print语句
python 的 print 语句简单粗暴，就是print。
| 输出目标 | print语句 |
|---|---|
| 输出字符串 | print(“字符串”)/print(‘字符串’) |
| 输出变量 | print(变量名) |
字符串与字符串之间，可以用逗号(,)或者加号(+)连接，变量名之间只能用加号连接。
与print相关的一些函数以及方法还有
列表list & 字典dic
列表和元组相似，区别在于元组中的数据不能更改而列表可以。它们二者的表现区别在于前者（列表）用方括号"[]“表示，而元组用圆括号”()"表示。
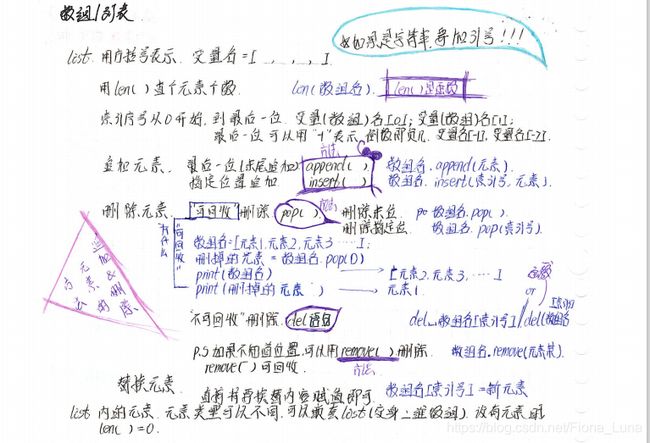
列表的相关函数有：
字典是由键值对组成的。
字典还可以与列表，字典进行嵌套。
循环 & 判断
python的循环和判断语句都是用缩进来表示的。
循环主要是for循环和while循环。
for 循环
while 循环
if 判断语句
函数 & 类class
函数
类
文件操作
从文件中读取数据
写入文件
存储数据
以上是本人个人整理的python基础语句。
在了解了python基础知识后，就是关于深度学习的学习了。
第二章 深度学习的基础知识
深度学习的简单介绍
近些年人工智能、机器学习和深度学习的概念十分火热，但很多从业者却很难说清它们之间的关系，外行人更是说到人工智能就只是一种“哇！很厉害哦。”的感叹。那么，这三者到底是什么关系？
人工智能、机器学习和深度学习覆盖的技术范畴是逐层递减的。人工智能是最宽泛的概念。机器学习是当前比较有效的一种实现人工智能的方式。深度学习是机器学习算法中最热门的一个分支，近些年取得了显著的进展，并替代了大多数传统机器学习算法。三者的关系如 图所示，即：人工智能 > 机器学习 > 深度学习。
人工智能
如字面含义，人工智能是研发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学。由于这个定义只阐述了目标，而没有限定方法，因此实现人工智能存在的诸多方法和分支，导致其变成一个“大杂烩”式的学科。
机器学习的实现
机器学习的实现可以分成两步：训练和预测，类似于我们熟悉的归纳和演绎：
归纳： 从具体案例中抽象一般规律，机器学习中的“训练”亦是如此。从一定数量的样本（已知模型输入X和模型输出Y）中，学习输出Y与输入X的关系（可以想象成是某种表达式）。
演绎： 从一般规律推导出具体案例的结果，机器学习中的“预测”亦是如此。基于训练得到的Y与X之间的关系，如出现新的输入X，计算出输出Y。通常情况下，如果通过模型计算的输出和真实场景的输出一致，则说明模型是有效的。
机器学习的方法论
课程从“牛顿第二定律”入手，介绍机器学习的思考过程，以及在过程中如何确定模型参数，模型三个关键部分（假设、评价、优化）该如何应用。其中：
- 模型假设：世界上的可能关系千千万，漫无目标的试探YX之间的关系显然是十分低效的。因此假设空间先圈定了一个模型能够表达的关系可能，如蓝色圆圈所示。机器还会进一步在假设圈定的圆圈内寻找最优的YX关系，即确定参数W。
- 评价函数：寻找最优之前，我们需要先定义什么是最优，即评价一个Y~X关系的好坏的指标。通常衡量该关系是否能很好的拟合现有观测样本，将拟合的误差最小作为优化目标。
- 优化算法：设置了评价指标后，就可以在假设圈定的范围内，将使得评价指标最优（损失函数最小/最拟合已有观测样本）的Y~X关系找出来，这个寻找的方法即为优化算法。最笨的优化算法即按照参数的可能，穷举每一个可能取值来计算损失函数，保留使得损失函数最小的参数作为最终结果。
在牛顿第二定律的学习过程中，以上三个部分分别是这样进行的：
- 假设：通过观察加速度a和作用力F的观测数据，假设aaa和FFF是线性关系，即a=w∗F。
- 评价：对已知观测数据上的拟合效果好，即w∗F计算的结果，要和观测的a尽量接近。
- 优化：在参数w的所有可能取值中，发现w=1/m可使得评价最好（最拟合观测样本）。
总而言之：机器执行学习的框架体现了其学习的本质是“参数估计”（Learning is parameter estimation）。
深度学习
机器学习算法理论在上个世纪90年代发展成熟，在许多领域都取得了成功应用。但平静的日子只延续到2010年左右，随着大数据的涌现和计算机算力提升，深度学习模型异军突起，极大改变了机器学习的应用格局。今天，多数机器学习任务都可以使用深度学习模型解决，尤其在在语音、计算机视觉和自然语言处理等领域，深度学习模型的效果比传统机器学习算法有显著提升。
相比传统的机器学习算法，深度学习在理论结构上与其基本是一致的，即：模型假设、评价函数和优化算法，其根本差别在于假设的复杂度。
神经网络的基本概念
人工神经网络包括多个神经网络层，如卷积层、全连接层、LSTM等，每一层又包括很多神经元，超过三层的非线性神经网络都可以被称为深度神经网络。通俗的讲，深度学习的模型可以视为是输入到输出的映射函数，足够深的神经网络理论上可以拟合任何复杂的函数。因此神经网络非常适合学习样本数据的内在规律和表示层次，对文字、图像和语音任务有很好的适用性。因为这几个领域的任务是人工智能的基础模块，所以深度学习被称为实现人工智能的基础也就不足为奇了。
神经网络结构如下所示。
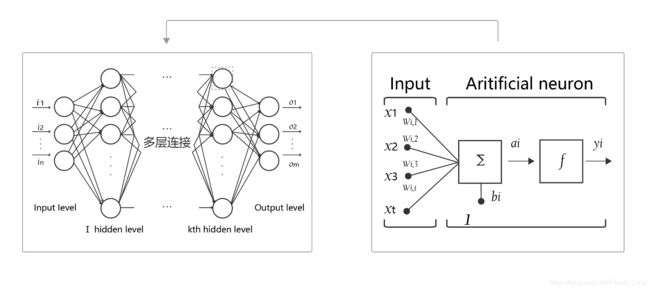
以上就是深度学习的一些基本理论知识。
理论知识晦涩难懂，需要反复研读，但是融入实践中就很容易理解了。
就比如一个牙牙学语的孩子，他对整个世界是陌生未知的。我们需要教导他“认识世界”。妈妈拿着“苹果”的识字卡，告诉宝宝，这是苹果。宝宝就会记住这个东西的基本特征，并记住“苹果”的发音。等再一次看到“苹果”的时候，正确的指出来。
深度学习也是一样，我们要告诉它，这个东西是“苹果”，它提取“苹果”的基本特征，并记住“苹果”的标签（label）。等下一次再看到“苹果”的时候正确的反馈出来。所以最困难的在于“苹果”的基本特征是什么。
程序结构“八股文”
深度学习的程序明显没有理论知识那么晦涩难懂。甚至有固定的“模板”，只要改变相应的内容就可以实现一个新的网络的搭建。（感谢前人种的树，使得后人可以乘凉：））
所有平台的程序结构大框架是基本一致，如图所示。
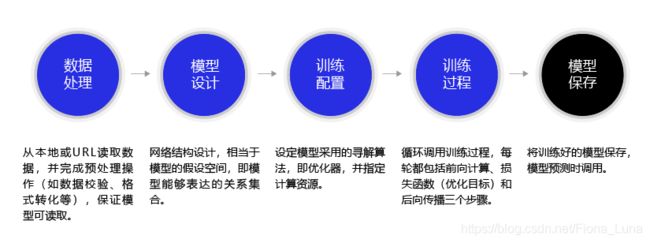
飞桨paddle具体的网络内容如下：
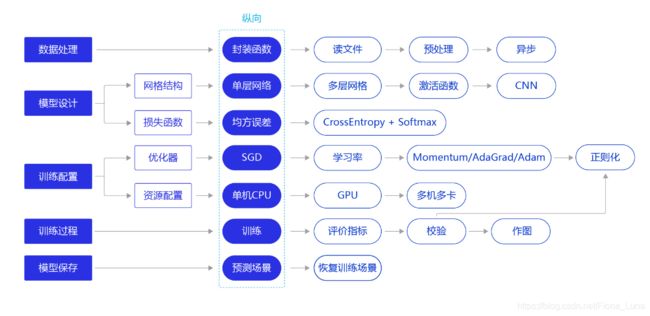
对于不同的网络模型，只需要横向改动其中相关内容即可。
第一个实践——mnist
课程以最基本的手写数字为例，向我们介绍如何使用“模板”来实现深度学习。
STEP 0
在数据处理前，首先要加载飞桨与手写数字识别模型相关的类库，实现方法如下。
#加载飞桨和相关类库
import paddle
import paddle.fluid as fluid
from paddle.fluid.dygraph.nn import Linear
import numpy as np
import os
from PIL import Image
STEP 1 数据处理
飞桨提供了多个封装好的数据集API，涵盖计算机视觉、自然语言处理、推荐系统等多个领域，帮助读者快速完成深度学习任务。如在手写数字识别任务中，通过paddle.dataset.mnist可以直接获取处理好的MNIST训练集、测试集。
如果已下载将会直接引用，若未下载将会先下载再直接引用。
通过*paddle.dataset.mnist.train()*函数设置数据读取器，batch_size设置为8，即一个批次有8张图片和8个标签，代码如下所示。
# 如果～/.cache/paddle/dataset/mnist/目录下没有MNIST数据，API会自动将MINST数据下载到该文件夹下
# 设置数据读取器，读取MNIST数据训练集
trainset = paddle.dataset.mnist.train()
# 包装数据读取器，每次读取的数据数量设置为batch_size=8
train_reader = paddle.batch(trainset, batch_size=8)
paddle.batch函数将MNIST数据集拆分成多个批次，通过如下代码读取第一个批次的数据内容，观察打印结果。
# 以迭代的形式读取数据
for batch_id, data in enumerate(train_reader()):
# 获得图像数据，并转为float32类型的数组
img_data = np.array([x[0] for x in data]).astype('float32')
# 获得图像标签数据，并转为float32类型的数组
label_data = np.array([x[1] for x in data]).astype('float32')
# 打印数据形状
print("图像数据形状和对应数据为:", img_data.shape, img_data[0])
print("图像标签形状和对应数据为:", label_data.shape, label_data[0])
break
在工业实践中，我们面临的任务和数据环境千差万别，通常需要自己编写适合当前任务的数据处理程序，一般涉及如下五个环节：
- 读入数据
- 划分数据集
- 生成批次数据
- 训练样本集乱序
- 校验数据有效性
读入数据 & 划分数据集
在实际应用中，保存到本地的数据存储格式多种多样，我们需要将它大致拆分为60%的训练集，20%的测试集，20%的验证集。
其中：
train_set（训练集）：包含50000条手写数字图片和对应的标签，用于确定模型参数。
val_set（验证集）：包含10000条手写数字图片和对应的标签，用于调节模型超参数（如多个网络结构、正则化权重的最优选择）。
test_set（测试集）：包含10000条手写数字图片和对应的标签，用于估计应用效果（没有在模型中应用过的数据，更贴近模型在真实场景应用的效果）。
train_set包含两个元素的列表：train_images、train_labels。
train_images：[5000, 784]的二维列表，包含5000张图片。每张图片用一个长度为784的向量表示，内容是28*28尺寸的像素灰度值（黑白图片）。
train_labels：[5000, ]的列表，表示这些图片对应的分类标签，即0-9之间的一个数字。
具体操作如下：
# 声明数据集文件位置
datafile = './work/mnist.json.gz'
print('loading mnist dataset from {} ......'.format(datafile))
# 加载json数据文件
data = json.load(gzip.open(datafile))
print('mnist dataset load done')
# 读取到的数据区分训练集，验证集，测试集
train_set, val_set, eval_set = data
# 数据集相关参数，图片高度IMG_ROWS, 图片宽度IMG_COLS
IMG_ROWS = 28
IMG_COLS = 28
# 打印数据信息
imgs, labels = train_set[0], train_set[1]
print("训练数据集数量: ", len(imgs))
# 观察验证集数量
imgs, labels = val_set[0], val_set[1]
print("验证数据集数量: ", len(imgs))
# 观察测试集数量
imgs, labels = val= eval_set[0], eval_set[1]
print("测试数据集数量: ", len(imgs))
训练样本乱序、生成批次数据
训练样本乱序： 先将样本按顺序进行编号，建立ID集合index_list。然后将index_list乱序，最后按乱序后的顺序读取数据。
说明：
通过大量实验发现，模型对最后出现的数据印象更加深刻。训练数据导入后，越接近模型训练结束，最后几个批次数据对模型参数的影响越大。为了避免模型记忆影响训练效果，需要进行样本乱序操作。
生成批次数据： 先设置合理的batch_size，再将数据转变成符合模型输入要求的np.array格式返回。同时，在返回数据时将Python生成器设置为yield模式，以减少内存占用。
在执行如上两个操作之前，需要先将数据处理代码封装成load_data函数，方便后续调用。load_data有三种模型：train、valid、eval，分为对应返回的数据是训练集、验证集、测试集。
具体操作如下：
imgs, labels = train_set[0], train_set[1]
print("训练数据集数量: ", len(imgs))
#获得数据集长度
imgs_length = len(imgs)
#定义数据集每个数据的序号，根据序号读取数据
index_list = list(range(imgs_length))
#读入数据时用到的批次大小
BATCHSIZE = 100
#随机打乱训练数据的索引序号
random.shuffle(index_list)
#定义数据生成器，返回批次数据
def data_generator():
imgs_list = []
labels_list = []
for i in index_list:
# 将数据处理成期望的格式，比如类型为float32，shape为[1, 28, 28]
img = np.reshape(imgs[i], [1, IMG_ROWS, IMG_COLS]).astype('float32')
label = np.reshape(labels[i], [1]).astype('float32')
imgs_list.append(img)
labels_list.append(label)
if len(imgs_list) == BATCHSIZE:
# 获得一个batchsize的数据，并返回
yield np.array(imgs_list), np.array(labels_list)
# 清空数据读取列表
imgs_list = []
labels_list = []
# 如果剩余数据的数目小于BATCHSIZE，
# 则剩余数据一起构成一个大小为len(imgs_list)的mini-batch
if len(imgs_list) > 0:
yield np.array(imgs_list), np.array(labels_list)
return data_generator
训练数据集数量: 50000
In [4]
#声明数据读取函数，从训练集中读取数据
train_loader = data_generator
#以迭代的形式读取数据
for batch_id, data in enumerate(train_loader()):
image_data, label_data = data
if batch_id == 0:
# 打印数据shape和类型
print("打印第一个batch数据的维度:")
print("图像维度: {}, 标签维度: {}".format(image_data.shape, label_data.shape))
break
校验数据有效性
在实际应用中，原始数据可能存在标注不准确、数据杂乱或格式不统一等情况。因此在完成数据处理流程后，还需要进行数据校验，一般有两种方式：
机器校验：加入一些校验和清理数据的操作。
人工校验：先打印数据输出结果，观察是否是设置的格式；再从训练的结果验证数据处理和读取的有效性。
机器校验
如下代码所示，如果数据集中的图片数量和标签数量不等，说明数据逻辑存在问题，可使用assert语句校验图像数量和标签数据是否一致。
imgs_length = len(imgs)
assert len(imgs) == len(labels), \
"length of train_imgs({}) should be the same as train_labels({})".format(len(imgs), len(label))
人工校验
人工校验是指打印数据输出结果，观察是否是预期的格式。实现数据处理和加载函数后，我们可以调用它读取一次数据，观察数据的shape和类型是否与函数中设置的一致。
#声明数据读取函数，从训练集中读取数据
train_loader = data_generator
#以迭代的形式读取数据
for batch_id, data in enumerate(train_loader()):
image_data, label_data = data
if batch_id == 0:
# 打印数据shape和类型
print("打印第一个batch数据的维度，以及数据的类型:")
print("图像维度: {}, 标签维度: {}, 图像数据类型: {}, 标签数据类型: {}".format(image_data.shape, label_data.shape, type(image_data), type(label_data)))
break
STEP 2 模型设计
1）网络结构
全连接神经网络
经典的全连接神经网络来包含四层网络：输入层、两个隐含层和输出层将手写数字识别任务通过全连接神经网络表示:
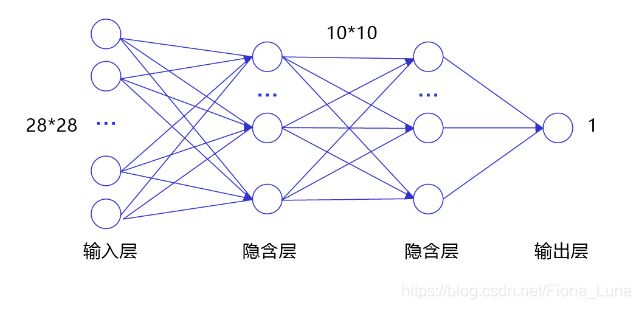
输入层：将数据输入给神经网络。在该任务中，输入层的尺度为28×28的像素值。
隐含层：增加网络深度和复杂度，隐含层的节点数是可以调整的，节点数越多，神经网络表示能力越强，参数量也会增加。在该任务中，中间的两个隐含层为10×10的结构，通常隐含层会比输入层的尺寸小，以便对关键信息做抽象，激活函数使用常见的sigmoid函数。
输出层：输出网络计算结果，输出层的节点数是固定的。如果是回归问题，节点数量为需要回归的数字数量；如果是分类问题，则是分类标签的数量。在该任务中，模型的输出是回归一个数字，输出层的尺寸为1。
下述代码为经典全连接神经网络的实现。
# 多层全连接神经网络实现
class MNIST(fluid.dygraph.Layer):
def __init__(self):
super(MNIST, self).__init__()
# 定义两层全连接隐含层，输出维度是10，激活函数为sigmoid
self.fc1 = Linear(input_dim=784, output_dim=10, act='sigmoid') # 隐含层节点为10，可根据任务调整
self.fc2 = Linear(input_dim=10, output_dim=10, act='sigmoid')
# 定义一层全连接输出层，输出维度是1，不使用激活函数
self.fc3 = Linear(input_dim=10, output_dim=1, act=None)
# 定义网络的前向计算
def forward(self, inputs, label=None):
inputs = fluid.layers.reshape(inputs, [inputs.shape[0], 784])
outputs1 = self.fc1(inputs)
outputs2 = self.fc2(outputs1)
outputs_final = self.fc3(outputs2)
return outputs_final
In [4]
#网络结构部分之后的代码，保持不变
with fluid.dygraph.guard():
model = MNIST()
model.train()
#调用加载数据的函数，获得MNIST训练数据集
train_loader = load_data('train')
# 使用SGD优化器，learning_rate设置为0.01
optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.01, parameter_list=model.parameters())
# 训练5轮
EPOCH_NUM = 5
for epoch_id in range(EPOCH_NUM):
for batch_id, data in enumerate(train_loader()):
#准备数据
image_data, label_data = data
image = fluid.dygraph.to_variable(image_data)
label = fluid.dygraph.to_variable(label_data)
#前向计算的过程
predict = model(image)
#计算损失，取一个批次样本损失的平均值
loss = fluid.layers.square_error_cost(predict, label)
avg_loss = fluid.layers.mean(loss)
#每训练了200批次的数据，打印下当前Loss的情况
if batch_id % 200 == 0:
print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))
#后向传播，更新参数的过程
avg_loss.backward()
optimizer.minimize(avg_loss)
model.clear_gradients()
#保存模型参数
fluid.save_dygraph(model.state_dict(), 'mnist')
卷积神经网络
虽然使用经典的全连接神经网络可以提升一定的准确率，但对于计算机视觉问题，效果最好的模型仍然是卷积神经网络。卷积神经网络针对视觉问题的特点进行了网络结构优化，更适合处理视觉问题。
卷积神经网络由多个卷积层和池化层组成，如图所示。卷积层负责对输入进行扫描以生成更抽象的特征表示，池化层对这些特征表示进行过滤，保留最关键的特征信息。
两层卷积和池化的卷积神经网络实现如下所示。
# 多层卷积神经网络实现
class MNIST(fluid.dygraph.Layer):
def __init__(self):
super(MNIST, self).__init__()
# 定义卷积层，输出特征通道num_filters设置为20，卷积核的大小filter_size为5，卷积步长stride=1，padding=2
# 激活函数使用relu
self.conv1 = Conv2D(num_channels=1, num_filters=20, filter_size=5, stride=1, padding=2, act='relu')
# 定义池化层，池化核pool_size=2，池化步长为2，选择最大池化方式
self.pool1 = Pool2D(pool_size=2, pool_stride=2, pool_type='max')
# 定义卷积层，输出特征通道num_filters设置为20，卷积核的大小filter_size为5，卷积步长stride=1，padding=2
self.conv2 = Conv2D(num_channels=20, num_filters=20, filter_size=5, stride=1, padding=2, act='relu')
# 定义池化层，池化核pool_size=2，池化步长为2，选择最大池化方式
self.pool2 = Pool2D(pool_size=2, pool_stride=2, pool_type='max')
# 定义一层全连接层，输出维度是1，不使用激活函数
self.fc = Linear(input_dim=980, output_dim=1, act=None)
# 定义网络前向计算过程，卷积后紧接着使用池化层，最后使用全连接层计算最终输出
def forward(self, inputs):
x = self.conv1(inputs)
x = self.pool1(x)
x = self.conv2(x)
x = self.pool2(x)
x = fluid.layers.reshape(x, [x.shape[0], -1])
x = self.fc(x)
return x
训练定义好的卷积神经网络，如下所示。
In [7]
#网络结构部分之后的代码，保持不变
with fluid.dygraph.guard():
model = MNIST()
model.train()
#调用加载数据的函数
train_loader = load_data('train')
optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.01, parameter_list=model.parameters())
EPOCH_NUM = 5
for epoch_id in range(EPOCH_NUM):
for batch_id, data in enumerate(train_loader()):
#准备数据
image_data, label_data = data
image = fluid.dygraph.to_variable(image_data)
label = fluid.dygraph.to_variable(label_data)
#前向计算的过程
predict = model(image)
#计算损失，取一个批次样本损失的平均值
loss = fluid.layers.square_error_cost(predict, label)
avg_loss = fluid.layers.mean(loss)
#每训练了200批次的数据，打印下当前Loss的情况
if batch_id % 200 == 0:
print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))
#后向传播，更新参数的过程
avg_loss.backward()
optimizer.minimize(avg_loss)
model.clear_gradients()
#保存模型参数
fluid.save_dygraph(model.state_dict(), 'mnist')
与经典全连接神经网络相比，卷积神经网络的损失值下降更快，且最终的损失值更小。
2）损失函数
损失函数是模型优化的目标，用于在众多的参数取值中，识别最理想的取值。损失函数的计算在训练过程的代码中，每一轮模型训练的过程都相同，分如下三步：
-
先根据输入数据正向计算预测输出。
-
再根据预测值和真实值计算损失。
-
最后根据损失反向传播梯度并更新参数。
Softmax函数
对于分类函数而言，如果模型能输出10个标签的概率，对应真实标签的概率输出尽可能接近100%，而其他标签的概率输出尽可能接近0%，且所有输出概率之和为1。这是一种更合理的假设！与此对应，真实的标签值可以转变成一个10维度的one-hot向量，在对应数字的位置上为1，其余位置为0，比如标签“6”可以转变成[0,0,0,0,0,0,1,0,0,0]。
为了实现上述思路，需要引入Softmax函数，它可以将原始输出转变成对应标签的概率，公式如下，其中C是标签类别个数。
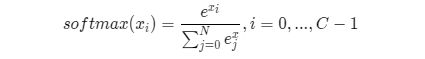
从公式的形式可见，每个输出的范围均在0~1之间，且所有输出之和等于1，这是变换后可被解释成概率的基本前提。对应到代码上，我们需要在网络定义部分修改输出层：self.fc = Linear(input_dim=10, output_dim=1, act=‘softmax’)，即是对全连接层的输出加一个softmax运算。
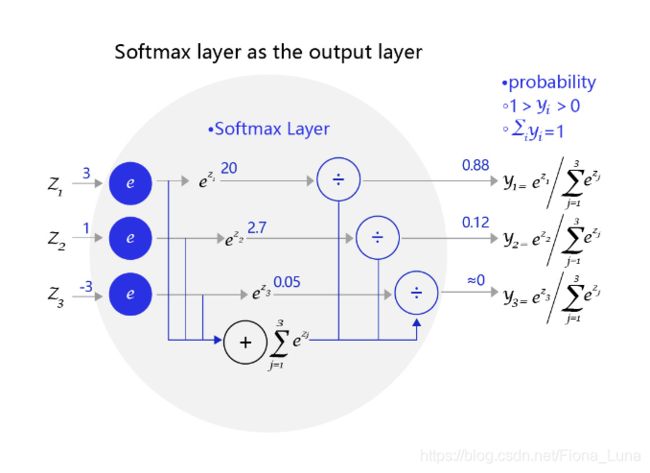
下图是一个三个标签的分类模型（三分类）使用的softmax输出层，从中可见原始输出的三个数字3、1、-3，经过softmax层后转变成加和为1的三个概率值0.88、0.12、0。
交叉熵
在模型输出为分类标签的概率时，直接以标签和概率做比较也不够合理，人们更习惯使用交叉熵误差作为分类问题的损失衡量。
交叉熵损失函数的设计是基于最大似然思想。
交叉熵的代码实现
在手写数字识别任务中，仅改动三行代码，就可以将在现有模型的损失函数替换成交叉熵（cross_entropy）。
在读取数据部分，将标签的类型设置成int，体现它是一个标签而不是实数值（飞桨默认将标签处理成“int64”）。
在网络定义部分，将输出层改成“输出十个标签的概率”的模式。
在训练过程部分，将损失函数从均方误差换成交叉熵。
在数据处理部分，需要修改标签变量Label的格式，代码如下所示。
- 从：label = np.reshape(labels[i], [1]).astype(‘float32’)
- 到：label = np.reshape(labels[i], [1]).astype(‘int64’)
具体代码如下：
#修改标签数据的格式，从float32到int64
import os
import random
import paddle
import paddle.fluid as fluid
from paddle.fluid.dygraph.nn import Conv2D, Pool2D, Linear
import numpy as np
from PIL import Image
import gzip
import json
# 定义数据集读取器
def load_data(mode='train'):
# 数据文件
datafile = './work/mnist.json.gz'
print('loading mnist dataset from {} ......'.format(datafile))
data = json.load(gzip.open(datafile))
train_set, val_set, eval_set = data
# 数据集相关参数，图片高度IMG_ROWS, 图片宽度IMG_COLS
IMG_ROWS = 28
IMG_COLS = 28
if mode == 'train':
imgs = train_set[0]
labels = train_set[1]
elif mode == 'valid':
imgs = val_set[0]
labels = val_set[1]
elif mode == 'eval':
imgs = eval_set[0]
labels = eval_set[1]
imgs_length = len(imgs)
assert len(imgs) == len(labels), \
"length of train_imgs({}) should be the same as train_labels({})".format(
len(imgs), len(labels))
index_list = list(range(imgs_length))
# 读入数据时用到的batchsize
BATCHSIZE = 100
# 定义数据生成器
def data_generator():
if mode == 'train':
random.shuffle(index_list)
imgs_list = []
labels_list = []
for i in index_list:
img = np.reshape(imgs[i], [1, IMG_ROWS, IMG_COLS]).astype('float32')
label = np.reshape(labels[i], [1]).astype('int64')
imgs_list.append(img)
labels_list.append(label)
if len(imgs_list) == BATCHSIZE:
yield np.array(imgs_list), np.array(labels_list)
imgs_list = []
labels_list = []
# 如果剩余数据的数目小于BATCHSIZE，
# 则剩余数据一起构成一个大小为len(imgs_list)的mini-batch
if len(imgs_list) > 0:
yield np.array(imgs_list), np.array(labels_list)
return data_generator
在网络定义部分，需要修改输出层结构，代码如下所示。
从：self.fc = Linear(input_dim=980, output_dim=1, act=None)
到：self.fc = Linear(input_dim=980, output_dim=10, act='softmax')
# 定义模型结构
class MNIST(fluid.dygraph.Layer):
def __init__(self):
super(MNIST, self).__init__()
# 定义一个卷积层，使用relu激活函数
self.conv1 = Conv2D(num_channels=1, num_filters=20, filter_size=5, stride=1, padding=2, act='relu')
# 定义一个池化层，池化核为2，步长为2，使用最大池化方式
self.pool1 = Pool2D(pool_size=2, pool_stride=2, pool_type='max')
# 定义一个卷积层，使用relu激活函数
self.conv2 = Conv2D(num_channels=20, num_filters=20, filter_size=5, stride=1, padding=2, act='relu')
# 定义一个池化层，池化核为2，步长为2，使用最大池化方式
self.pool2 = Pool2D(pool_size=2, pool_stride=2, pool_type='max')
# 定义一个全连接层，输出节点数为10
self.fc = Linear(input_dim=980, output_dim=10, act='softmax')
# 定义网络的前向计算过程
def forward(self, inputs):
x = self.conv1(inputs)
x = self.pool1(x)
x = self.conv2(x)
x = self.pool2(x)
x = fluid.layers.reshape(x, [x.shape[0], 980])
x = self.fc(x)
return x
修改计算损失的函数，从均方误差（常用于回归问题）到交叉熵误差（常用于分类问题），代码如下所示。
从：loss = fluid.layers.square_error_cost(predict, label)
到：loss = fluid.layers.cross_entropy(predict, label)
#仅修改计算损失的函数，从均方误差（常用于回归问题）到交叉熵误差（常用于分类问题）
with fluid.dygraph.guard():
model = MNIST()
model.train()
#调用加载数据的函数
train_loader = load_data('train')
optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.01, parameter_list=model.parameters())
EPOCH_NUM = 5
for epoch_id in range(EPOCH_NUM):
for batch_id, data in enumerate(train_loader()):
#准备数据，变得更加简洁
image_data, label_data = data
image = fluid.dygraph.to_variable(image_data)
label = fluid.dygraph.to_variable(label_data)
#前向计算的过程
predict = model(image)
#计算损失，使用交叉熵损失函数，取一个批次样本损失的平均值
loss = fluid.layers.cross_entropy(predict, label)
avg_loss = fluid.layers.mean(loss)
#每训练了200批次的数据，打印下当前Loss的情况
if batch_id % 200 == 0:
print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))
#后向传播，更新参数的过程
avg_loss.backward()
optimizer.minimize(avg_loss)
model.clear_gradients()
#保存模型参数
fluid.save_dygraph(model.state_dict(), 'mnist')
由于我们修改了模型的输出格式，因此使用模型做预测时的代码也需要做相应的调整。从模型输出10个标签的概率中选择最大的，将其标签编号输出。
# 读取一张本地的样例图片，转变成模型输入的格式
def load_image(img_path):
# 从img_path中读取图像，并转为灰度图
im = Image.open(img_path).convert('L')
im.show()
im = im.resize((28, 28), Image.ANTIALIAS)
im = np.array(im).reshape(1, 1, 28, 28).astype(np.float32)
# 图像归一化
im = 1.0 - im / 255.
return im
# 定义预测过程
with fluid.dygraph.guard():
model = MNIST()
params_file_path = 'mnist'
img_path = './work/example_0.jpg'
# 加载模型参数
model_dict, _ = fluid.load_dygraph("mnist")
model.load_dict(model_dict)
model.eval()
tensor_img = load_image(img_path)
#模型反馈10个分类标签的对应概率
results = model(fluid.dygraph.to_variable(tensor_img))
#取概率最大的标签作为预测输出
lab = np.argsort(results.numpy())
print("本次预测的数字是: ", lab[0][-1])
STEP 3 训练配置
1）优化算法
在介绍了分类任务的损失函数（优化目标）的相关概念和实现方法后，课程向我们介绍了在手写数字识别任务中，使得损失达到最小的参数取值的实现方法。
设置学习率
在深度学习神经网络模型中，通常使用标准的随机梯度下降算法更新参数，学习率代表参数更新幅度的大小，即步长。当学习率最优时，模型的有效容量最大，最终能达到的效果最好。学习率和深度学习任务类型有关，合适的学习率往往需要大量的实验和调参经验。探索学习率最优值时需要注意如下两点：
-
学习率不是越小越好。学习率越小，损失函数的变化速度越慢，意味着我们需要花费更长的时间进行收敛，如图左所示。
-
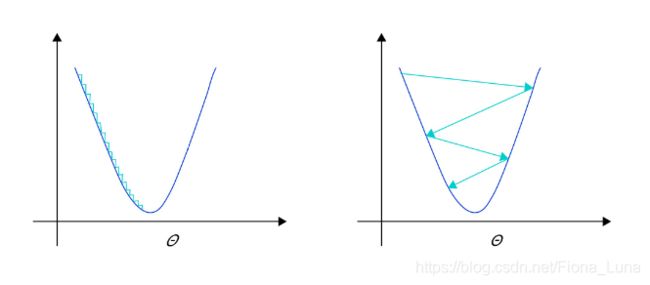
学习率不是越大越好。只根据总样本集中的一个批次计算梯度，抽样误差会导致计算出的梯度不是全局最优的方向，且存在波动。在接近最优解时，过大的学习率会导致参数在最优解附近震荡，损失难以收敛，如图右所示。
在训练前，我们往往不清楚一个特定问题设置成怎样的学习率是合理的，因此在训练时可以尝试调小或调大，通过观察Loss下降的情况判断合理的学习率，设置学习率的代码如下所示。
#仅优化算法的设置有所差别
with fluid.dygraph.guard():
model = MNIST()
model.train()
#调用加载数据的函数
train_loader = load_data('train')
#设置不同初始学习率
optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.01, parameter_list=model.parameters())
# optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.001, parameter_list=model.parameters())
# optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.1, parameter_list=model.parameters())
EPOCH_NUM = 5
for epoch_id in range(EPOCH_NUM):
for batch_id, data in enumerate(train_loader()):
#准备数据，变得更加简洁
image_data, label_data = data
image = fluid.dygraph.to_variable(image_data)
label = fluid.dygraph.to_variable(label_data)
#前向计算的过程
predict = model(image)
#计算损失，取一个批次样本损失的平均值
loss = fluid.layers.cross_entropy(predict, label)
avg_loss = fluid.layers.mean(loss)
#每训练了200批次的数据，打印下当前Loss的情况
if batch_id % 200 == 0:
print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))
#后向传播，更新参数的过程
avg_loss.backward()
optimizer.minimize(avg_loss)
model.clear_gradients()
#保存模型参数
fluid.save_dygraph(model.state_dict(), 'mnist')
学习率的主流优化算法
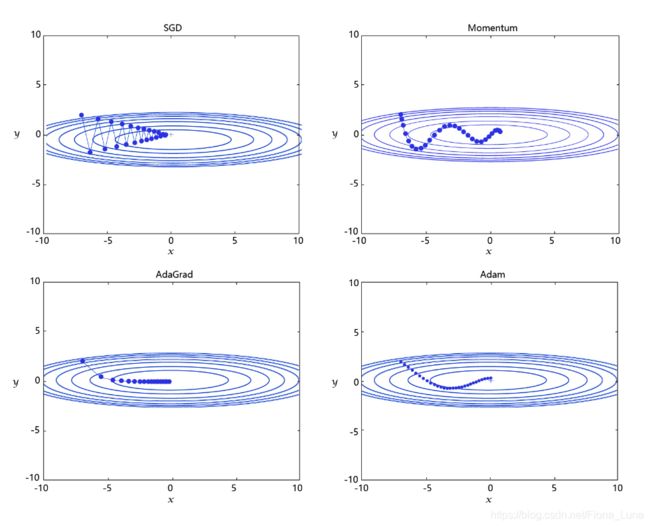
学习率是优化器的一个参数，调整学习率看似是一件非常麻烦的事情，需要不断的调整步长，观察训练时间和Loss的变化。经过研究员的不断的实验，当前已经形成了四种比较成熟的优化算法：SGD、Momentum、AdaGrad和Adam，效果如图所示。
-
SGD： 随机梯度下降算法，每次训练少量数据，抽样偏差导致参数收敛过程中震荡。
-
Momentum： 引入物理“动量”的概念，累积速度，减少震荡，使参数更新的方向更稳定。
每个批次的数据含有抽样误差，导致梯度更新的方向波动较大。如果我们引入物理动量的概念，给梯度下降的过程加入一定的“惯性”累积，就可以减少更新路径上的震荡，即每次更新的梯度由“历史多次梯度的累积方向”和“当次梯度”加权相加得到。历史多次梯度的累积方向往往是从全局视角更正确的方向，这与“惯性”的物理概念很像，也是为何其起名为“Momentum”的原因。类似不同品牌和材质的篮球有一定的重量差别，街头篮球队中的投手（擅长中远距离投篮）喜欢稍重篮球的比例较高。一个很重要的原因是，重的篮球惯性大，更不容易受到手势的小幅变形或风吹的影响。
-
AdaGrad： 根据不同参数距离最优解的远近，动态调整学习率。学习率逐渐下降，依据各参数变化大小调整学习率。
通过调整学习率的实验可以发现：当某个参数的现值距离最优解较远时（表现为梯度的绝对值较大），我们期望参数更新的步长大一些，以便更快收敛到最优解。当某个参数的现值距离最优解较近时（表现为梯度的绝对值较小），我们期望参数的更新步长小一些，以便更精细的逼近最优解。类似于打高尔夫球，专业运动员第一杆开球时，通常会大力打一个远球，让球尽量落在洞口附近。当第二杆面对离洞口较近的球时，他会更轻柔而细致的推杆，避免将球打飞。与此类似，参数更新的步长应该随着优化过程逐渐减少，减少的程度与当前梯度的大小有关。根据这个思想编写的优化算法称为“AdaGrad”，Ada是Adaptive的缩写，表示“适应环境而变化”的意思。RMSProp是在AdaGrad基础上的改进，AdaGrad会累加之前所有的梯度平方，而RMSprop仅仅是计算对应的梯度平均值，因而可以解决AdaGrad学习率急剧下降的问题。 -
Adam： 由于动量和自适应学习率两个优化思路是正交的，因此可以将两个思路结合起来，这就是当前广泛应用的算法。
我们可以尝试选择不同的优化算法训练模型，观察训练时间和损失变化的情况，代码实现如下。
#仅优化算法的设置有所差别
with fluid.dygraph.guard():
model = MNIST()
model.train()
#调用加载数据的函数
train_loader = load_data('train')
#四种优化算法的设置方案，可以逐一尝试效果
optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.01, parameter_list=model.parameters())
#optimizer = fluid.optimizer.MomentumOptimizer(learning_rate=0.01, momentum=0.9, parameter_list=model.parameters())
#optimizer = fluid.optimizer.AdagradOptimizer(learning_rate=0.01, parameter_list=model.parameters())
#optimizer = fluid.optimizer.AdamOptimizer(learning_rate=0.01, parameter_list=model.parameters())
EPOCH_NUM = 5
for epoch_id in range(EPOCH_NUM):
for batch_id, data in enumerate(train_loader()):
#准备数据，变得更加简洁
image_data, label_data = data
image = fluid.dygraph.to_variable(image_data)
label = fluid.dygraph.to_variable(label_data)
#前向计算的过程
predict = model(image)
#计算损失，取一个批次样本损失的平均值
loss = fluid.layers.cross_entropy(predict, label)
avg_loss = fluid.layers.mean(loss)
#每训练了200批次的数据，打印下当前Loss的情况
if batch_id % 200 == 0:
print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))
#后向传播，更新参数的过程
avg_loss.backward()
optimizer.minimize(avg_loss)
model.clear_gradients()
#保存模型参数
fluid.save_dygraph(model.state_dict(), 'mnist')
2）资源配置
当我们遇到复杂的机器学习或深度学习任务时，需要运算速度更高的硬件（如GPU、NPU），甚至同时使用多个机器共同训练一个任务（多卡训练和多机训练）。课程在本节向我们介绍了如何通过资源配置的优化，提升模型训练效率。
单GPU训练
飞桨动态图通过fluid.dygraph.guard(place=None)里的place参数，设置在GPU上训练还是CPU上训练。
with fluid.dygraph.guard(place=fluid.CPUPlace()) #设置使用CPU资源训神经网络。
with fluid.dygraph.guard(place=fluid.CUDAPlace(0)) #设置使用GPU资源训神经网络，默认使用服务器的第一个GPU卡。"0"是GPU卡的编号，比如一台服务器有的四个GPU卡，编号分别为０、１、２、３。
#仅前3行代码有所变化，在使用GPU时，可以将use_gpu变量设置成True
use_gpu = False
place = fluid.CUDAPlace(0) if use_gpu else fluid.CPUPlace()
with fluid.dygraph.guard(place):
model = MNIST()
model.train()
#调用加载数据的函数
train_loader = load_data('train')
#四种优化算法的设置方案，可以逐一尝试效果
optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.01, parameter_list=model.parameters())
#optimizer = fluid.optimizer.MomentumOptimizer(learning_rate=0.01, momentum=0.9, parameter_list=model.parameters())
#optimizer = fluid.optimizer.AdagradOptimizer(learning_rate=0.01, parameter_list=model.parameters())
#optimizer = fluid.optimizer.AdamOptimizer(learning_rate=0.01, parameter_list=model.parameters())
EPOCH_NUM = 2
for epoch_id in range(EPOCH_NUM):
for batch_id, data in enumerate(train_loader()):
#准备数据，变得更加简洁
image_data, label_data = data
image = fluid.dygraph.to_variable(image_data)
label = fluid.dygraph.to_variable(label_data)
#前向计算的过程
predict = model(image)
#计算损失，取一个批次样本损失的平均值
loss = fluid.layers.cross_entropy(predict, label)
avg_loss = fluid.layers.mean(loss)
#每训练了200批次的数据，打印下当前Loss的情况
if batch_id % 200 == 0:
print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))
#后向传播，更新参数的过程
avg_loss.backward()
optimizer.minimize(avg_loss)
model.clear_gradients()
#保存模型参数
fluid.save_dygraph(model.state_dict(), 'mnist')
分布式训练
在工业实践中，很多较复杂的任务需要使用更强大的模型。强大模型加上海量的训练数据，经常导致模型训练耗时严重。比如在计算机视觉分类任务中，训练一个在ImageNet数据集上精度表现良好的模型，大概需要一周的时间，因为过程中我们需要不断尝试各种优化的思路和方案。如果每次训练均要耗时1周，这会大大降低模型迭代的速度。在机器资源充沛的情况下，建议采用分布式训练，大部分模型的训练时间可压缩到小时级别。
分布式训练有两种实现模式：模型并行和数据并行。
模型并行
模型并行是将一个网络模型拆分为多份，拆分后的模型分到多个设备上（GPU）训练，每个设备的训练数据是相同的。模型并行的实现模式可以节省内存，但是应用较为受限。
模型并行的方式一般适用于如下两个场景：
-
模型架构过大： 完整的模型无法放入单个GPU。如2012年ImageNet大赛的冠军模型AlexNet是模型并行的典型案例，由于当时GPU内存较小，单个GPU不足以承担AlexNet，因此研究者将AlexNet拆分为两部分放到两个GPU上并行训练。
-
网络模型的结构设计相对独立： 当网络模型的设计结构可以并行化时，采用模型并行的方式。如在计算机视觉目标检测任务中，一些模型（如YOLO9000）的边界框回归和类别预测是独立的，可以将独立的部分放到不同的设备节点上完成分布式训练。
数据并行
数据并行与模型并行不同，数据并行每次读取多份数据，读取到的数据输入给多个设备（GPU）上的模型，每个设备上的模型是完全相同的，飞桨采用的就是这种方式。
STEP 4 训练过程
训练调试与优化
之前我们研究了资源部署优化的方法，通过使用单GPU和分布式部署，提升模型训练的效率。现在我们讨论为了保证模型的真实效果，在模型训练部分，对模型进行一些调试和优化的方法。
训练过程优化思路主要有如下五个关键环节：
- 计算分类准确率，观测模型训练效果。
交叉熵损失函数只能作为优化目标，无法直接准确衡量模型的训练效果。准确率可以直接衡量训练效果，但由于其离散性质，不适合做为损失函数优化神经网络。
- 检查模型训练过程，识别潜在问题。
如果模型的损失或者评估指标表现异常，通常需要打印模型每一层的输入和输出来定位问题，分析每一层的内容来获取错误的原因。
- 加入校验或测试，更好评价模型效果。
理想的模型训练结果是在训练集和验证集上均有较高的准确率，如果训练集上的准确率高于验证集，说明网络训练程度不够；如果验证集的准确率高于训练集，可能是发生了过拟合现象。通过在优化目标中加入正则化项的办法，解决过拟合的问题。
- 加入正则化项，避免模型过拟合。
飞桨框架支持为整体参数加入正则化项，这是通常的做法。此外，飞桨框架也支持为某一层或某一部分的网络单独加入正则化项，以达到精细调整参数训练的效果。
- 可视化分析。
用户不仅可以通过打印或使用matplotlib库作图，飞桨还提供了更专业的可视化分析工具VisualDL，提供便捷的可视化分析方法。
计算模型的分类准确率
准确率是一个直观衡量分类模型效果的指标，由于这个指标是离散的，因此不适合作为损失函数来优化。通常情况下，交叉熵损失越小的模型，分类的准确率也越高。基于分类准确率，我们可以公平的比较两种损失函数的优劣，例如【手写数字识别】之损失函数 章节中均方误差和交叉熵的比较。
飞桨提供了计算分类准确率的API，使用fluid.layers.accuracy可以直接计算准确率，该API的输入参数input为预测的分类结果predict，输入参数label为数据真实的label。
在下述代码中，我们在模型前向计算过程forward函数中计算分类准确率，并在训练时打印每个批次样本的分类准确率。
# 加载相关库
import os
import random
import paddle
import paddle.fluid as fluid
from paddle.fluid.dygraph.nn import Conv2D, Pool2D, Linear
import numpy as np
from PIL import Image
import gzip
import json
# 定义数据集读取器
def load_data(mode='train'):
# 读取数据文件
datafile = './work/mnist.json.gz'
print('loading mnist dataset from {} ......'.format(datafile))
data = json.load(gzip.open(datafile))
# 读取数据集中的训练集，验证集和测试集
train_set, val_set, eval_set = data
# 数据集相关参数，图片高度IMG_ROWS, 图片宽度IMG_COLS
IMG_ROWS = 28
IMG_COLS = 28
# 根据输入mode参数决定使用训练集，验证集还是测试
if mode == 'train':
imgs = train_set[0]
labels = train_set[1]
elif mode == 'valid':
imgs = val_set[0]
labels = val_set[1]
elif mode == 'eval':
imgs = eval_set[0]
labels = eval_set[1]
# 获得所有图像的数量
imgs_length = len(imgs)
# 验证图像数量和标签数量是否一致
assert len(imgs) == len(labels), \
"length of train_imgs({}) should be the same as train_labels({})".format(
len(imgs), len(labels))
index_list = list(range(imgs_length))
# 读入数据时用到的batchsize
BATCHSIZE = 100
# 定义数据生成器
def data_generator():
# 训练模式下，打乱训练数据
if mode == 'train':
random.shuffle(index_list)
imgs_list = []
labels_list = []
# 按照索引读取数据
for i in index_list:
# 读取图像和标签，转换其尺寸和类型
img = np.reshape(imgs[i], [1, IMG_ROWS, IMG_COLS]).astype('float32')
label = np.reshape(labels[i], [1]).astype('int64')
imgs_list.append(img)
labels_list.append(label)
# 如果当前数据缓存达到了batch size，就返回一个批次数据
if len(imgs_list) == BATCHSIZE:
yield np.array(imgs_list), np.array(labels_list)
# 清空数据缓存列表
imgs_list = []
labels_list = []
# 如果剩余数据的数目小于BATCHSIZE，
# 则剩余数据一起构成一个大小为len(imgs_list)的mini-batch
if len(imgs_list) > 0:
yield np.array(imgs_list), np.array(labels_list)
return data_generator
# 定义模型结构
class MNIST(fluid.dygraph.Layer):
def __init__(self):
super(MNIST, self).__init__()
# 定义一个卷积层，使用relu激活函数
self.conv1 = Conv2D(num_channels=1, num_filters=20, filter_size=5, stride=1, padding=2, act='relu')
# 定义一个池化层，池化核为2，步长为2，使用最大池化方式
self.pool1 = Pool2D(pool_size=2, pool_stride=2, pool_type='max')
# 定义一个卷积层，使用relu激活函数
self.conv2 = Conv2D(num_channels=20, num_filters=20, filter_size=5, stride=1, padding=2, act='relu')
# 定义一个池化层，池化核为2，步长为2，使用最大池化方式
self.pool2 = Pool2D(pool_size=2, pool_stride=2, pool_type='max')
# 定义一个全连接层，输出节点数为10
self.fc = Linear(input_dim=980, output_dim=10, act='softmax')
# 定义网络的前向计算过程
def forward(self, inputs, label):
x = self.conv1(inputs)
x = self.pool1(x)
x = self.conv2(x)
x = self.pool2(x)
x = fluid.layers.reshape(x, [x.shape[0], 980])
x = self.fc(x)
if label is not None:
acc = fluid.layers.accuracy(input=x, label=label)
return x, acc
else:
return x
#调用加载数据的函数
train_loader = load_data('train')
#在使用GPU机器时，可以将use_gpu变量设置成True
use_gpu = False
place = fluid.CUDAPlace(0) if use_gpu else fluid.CPUPlace()
with fluid.dygraph.guard(place):
model = MNIST()
model.train()
#四种优化算法的设置方案，可以逐一尝试效果
optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.01, parameter_list=model.parameters())
#optimizer = fluid.optimizer.MomentumOptimizer(learning_rate=0.01, momentum=0.9, parameter_list=model.parameters())
#optimizer = fluid.optimizer.AdagradOptimizer(learning_rate=0.01, parameter_list=model.parameters())
#optimizer = fluid.optimizer.AdamOptimizer(learning_rate=0.01, parameter_list=model.parameters())
EPOCH_NUM = 5
for epoch_id in range(EPOCH_NUM):
for batch_id, data in enumerate(train_loader()):
#准备数据
image_data, label_data = data
image = fluid.dygraph.to_variable(image_data)
label = fluid.dygraph.to_variable(label_data)
#前向计算的过程，同时拿到模型输出值和分类准确率
predict, acc = model(image, label)
#计算损失，取一个批次样本损失的平均值
loss = fluid.layers.cross_entropy(predict, label)
avg_loss = fluid.layers.mean(loss)
#每训练了200批次的数据，打印下当前Loss的情况
if batch_id % 200 == 0:
print("epoch: {}, batch: {}, loss is: {}, acc is {}".format(epoch_id, batch_id, avg_loss.numpy(), acc.numpy()))
#后向传播，更新参数的过程
avg_loss.backward()
optimizer.minimize(avg_loss)
model.clear_gradients()
#保存模型参数
fluid.save_dygraph(model.state_dict(), 'mnist')
检查模型训练过程，识别潜在训练问题
使用飞桨动态图可以方便的查看和调试训练的执行过程。在网络定义的Forward函数中，可以打印每一层输入输出的尺寸，以及每层网络的参数。通过查看这些信息，不仅可以更好地理解训练的执行过程，还可以发现潜在问题，或者启发继续优化的思路。
在下述程序中，使用check_shape变量控制是否打印“尺寸”，验证网络结构是否正确。使用check_content变量控制是否打印“内容值”，验证数据分布是否合理。假如在训练中发现中间层的部分输出持续为0，说明该部分的网络结构设计存在问题，没有充分利用。
# 定义模型结构
class MNIST(fluid.dygraph.Layer):
def __init__(self):
super(MNIST, self).__init__()
# 定义一个卷积层，使用relu激活函数
self.conv1 = Conv2D(num_channels=1, num_filters=20, filter_size=5, stride=1, padding=2, act='relu')
# 定义一个池化层，池化核为2，步长为2，使用最大池化方式
self.pool1 = Pool2D(pool_size=2, pool_stride=2, pool_type='max')
# 定义一个卷积层，使用relu激活函数
self.conv2 = Conv2D(num_channels=20, num_filters=20, filter_size=5, stride=1, padding=2, act='relu')
# 定义一个池化层，池化核为2，步长为2，使用最大池化方式
self.pool2 = Pool2D(pool_size=2, pool_stride=2, pool_type='max')
# 定义一个全连接层，输出节点数为10
self.fc = Linear(input_dim=980, output_dim=10, act='softmax')
# 加入对每一层输入和输出的尺寸和数据内容的打印，根据check参数决策是否打印每层的参数和输出尺寸
def forward(self, inputs, label=None, check_shape=False, check_content=False):
# 给不同层的输出不同命名，方便调试
outputs1 = self.conv1(inputs)
outputs2 = self.pool1(outputs1)
outputs3 = self.conv2(outputs2)
outputs4 = self.pool2(outputs3)
_outputs4 = fluid.layers.reshape(outputs4, [outputs4.shape[0], -1])
outputs5 = self.fc(_outputs4)
# 选择是否打印神经网络每层的参数尺寸和输出尺寸，验证网络结构是否设置正确
if check_shape:
# 打印每层网络设置的超参数-卷积核尺寸，卷积步长，卷积padding，池化核尺寸
print("\n########## print network layer's superparams ##############")
print("conv1-- kernel_size:{}, padding:{}, stride:{}".format(self.conv1.weight.shape, self.conv1._padding, self.conv1._stride))
print("conv2-- kernel_size:{}, padding:{}, stride:{}".format(self.conv2.weight.shape, self.conv2._padding, self.conv2._stride))
print("pool1-- pool_type:{}, pool_size:{}, pool_stride:{}".format(self.pool1._pool_type, self.pool1._pool_size, self.pool1._pool_stride))
print("pool2-- pool_type:{}, poo2_size:{}, pool_stride:{}".format(self.pool2._pool_type, self.pool2._pool_size, self.pool2._pool_stride))
print("fc-- weight_size:{}, bias_size_{}, activation:{}".format(self.fc.weight.shape, self.fc.bias.shape, self.fc._act))
# 打印每层的输出尺寸
print("\n########## print shape of features of every layer ###############")
print("inputs_shape: {}".format(inputs.shape))
print("outputs1_shape: {}".format(outputs1.shape))
print("outputs2_shape: {}".format(outputs2.shape))
print("outputs3_shape: {}".format(outputs3.shape))
print("outputs4_shape: {}".format(outputs4.shape))
print("outputs5_shape: {}".format(outputs5.shape))
# 选择是否打印训练过程中的参数和输出内容，可用于训练过程中的调试
if check_content:
# 打印卷积层的参数-卷积核权重，权重参数较多，此处只打印部分参数
print("\n########## print convolution layer's kernel ###############")
print("conv1 params -- kernel weights:", self.conv1.weight[0][0])
print("conv2 params -- kernel weights:", self.conv2.weight[0][0])
# 创建随机数，随机打印某一个通道的输出值
idx1 = np.random.randint(0, outputs1.shape[1])
idx2 = np.random.randint(0, outputs3.shape[1])
# 打印卷积-池化后的结果，仅打印batch中第一个图像对应的特征
print("\nThe {}th channel of conv1 layer: ".format(idx1), outputs1[0][idx1])
print("The {}th channel of conv2 layer: ".format(idx2), outputs3[0][idx2])
print("The output of last layer:", outputs5[0], '\n')
# 如果label不是None，则计算分类精度并返回
if label is not None:
acc = fluid.layers.accuracy(input=outputs5, label=label)
return outputs5, acc
else:
return outputs5
#在使用GPU机器时，可以将use_gpu变量设置成True
use_gpu = False
place = fluid.CUDAPlace(0) if use_gpu else fluid.CPUPlace()
with fluid.dygraph.guard(place):
model = MNIST()
model.train()
#四种优化算法的设置方案，可以逐一尝试效果
optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.01, parameter_list=model.parameters())
#optimizer = fluid.optimizer.MomentumOptimizer(learning_rate=0.01, momentum=0.9, parameter_list=model.parameters())
#optimizer = fluid.optimizer.AdagradOptimizer(learning_rate=0.01, parameter_list=model.parameters())
#optimizer = fluid.optimizer.AdamOptimizer(learning_rate=0.01, parameter_list=model.parameters())
EPOCH_NUM = 1
for epoch_id in range(EPOCH_NUM):
for batch_id, data in enumerate(train_loader()):
#准备数据，变得更加简洁
image_data, label_data = data
image = fluid.dygraph.to_variable(image_data)
label = fluid.dygraph.to_variable(label_data)
#前向计算的过程，同时拿到模型输出值和分类准确率
if batch_id == 0 and epoch_id==0:
# 打印模型参数和每层输出的尺寸
predict, acc = model(image, label, check_shape=True, check_content=False)
elif batch_id==401:
# 打印模型参数和每层输出的值
predict, acc = model(image, label, check_shape=False, check_content=True)
else:
predict, acc = model(image, label)
#计算损失，取一个批次样本损失的平均值
loss = fluid.layers.cross_entropy(predict, label)
avg_loss = fluid.layers.mean(loss)
#每训练了100批次的数据，打印下当前Loss的情况
if batch_id % 200 == 0:
print("epoch: {}, batch: {}, loss is: {}, acc is {}".format(epoch_id, batch_id, avg_loss.numpy(), acc.numpy()))
#后向传播，更新参数的过程
avg_loss.backward()
optimizer.minimize(avg_loss)
model.clear_gradients()
#保存模型参数
fluid.save_dygraph(model.state_dict(), 'mnist')
print("Model has been saved.")
加入校验或测试，更好评价模型效果
在训练过程中，我们会发现模型在训练样本集上的损失在不断减小。但这是否代表模型在未来的应用场景上依然有效？为了验证模型的有效性，通常将样本集合分成三份，训练集、校验集和测试集。
**训练集 **：用于训练模型的参数，即训练过程中主要完成的工作。
校验集 ：用于对模型超参数的选择，比如网络结构的调整、正则化项权重的选择等。
**测试集 **：用于模拟模型在应用后的真实效果。因为测试集没有参与任何模型优化或参数训练的工作，所以它对模型来说是完全未知的样本。在不以校验数据优化网络结构或模型超参数时，校验数据和测试数据的效果是类似的，均更真实的反映模型效果。
如下程序读取上一步训练保存的模型参数，读取测试数据集，并测试模型在测试数据集上的效果。
with fluid.dygraph.guard():
print('start evaluation .......')
#加载模型参数
model = MNIST()
model_state_dict, _ = fluid.load_dygraph('mnist')
model.load_dict(model_state_dict)
model.eval()
eval_loader = load_data('eval')
acc_set = []
avg_loss_set = []
for batch_id, data in enumerate(eval_loader()):
x_data, y_data = data
img = fluid.dygraph.to_variable(x_data)
label = fluid.dygraph.to_variable(y_data)
prediction, acc = model(img, label)
loss = fluid.layers.cross_entropy(input=prediction, label=label)
avg_loss = fluid.layers.mean(loss)
acc_set.append(float(acc.numpy()))
avg_loss_set.append(float(avg_loss.numpy()))
#计算多个batch的平均损失和准确率
acc_val_mean = np.array(acc_set).mean()
avg_loss_val_mean = np.array(avg_loss_set).mean()
print('loss={}, acc={}'.format(avg_loss_val_mean, acc_val_mean))
加入正则化项，避免模型过拟合
过拟合现象
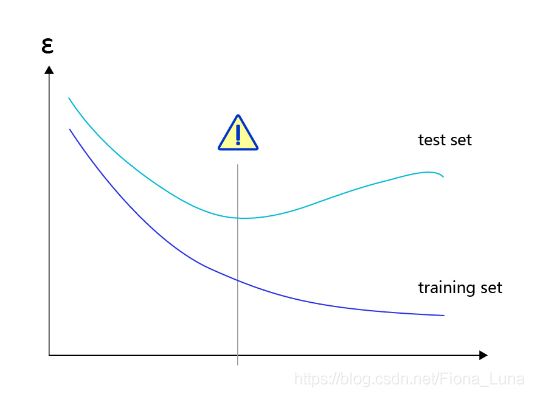
对于样本量有限、但需要使用强大模型的复杂任务，模型很容易出现过拟合的表现，即在训练集上的损失小，在验证集或测试集上的损失较大，如图所示。
反之，如果模型在训练集和测试集上均损失较大，则称为欠拟合。过拟合表示模型过于敏感，学习到了训练数据中的一些误差，而这些误差并不是真实的泛化规律（可推广到测试集上的规律）。欠拟合表示模型还不够强大，还没有很好的拟合已知的训练样本，更别提测试样本了。因为欠拟合情况容易观察和解决，只要训练loss不够好，就不断使用更强大的模型即可，因此实际中我们更需要处理好过拟合的问题。
导致过拟合原因
造成过拟合的原因是模型过于敏感，而训练数据量太少或其中的噪音太多。
如图所示，理想的回归模型是一条坡度较缓的抛物线，欠拟合的模型只拟合出一条直线，显然没有捕捉到真实的规律，但过拟合的模型拟合出存在很多拐点的抛物线，显然是过于敏感，也没有正确表达真实规律。
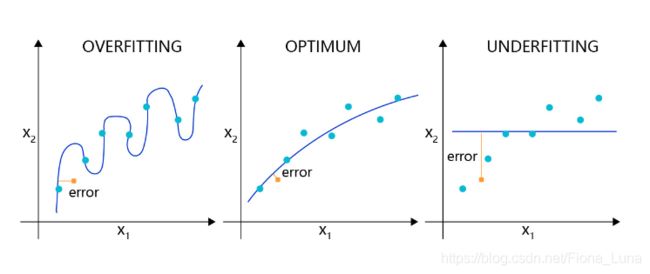
如所示，理想的分类模型是一条半圆形的曲线，欠拟合用直线作为分类边界，显然没有捕捉到真实的边界，但过拟合的模型拟合出很扭曲的分类边界，虽然对所有的训练数据正确分类，但对一些较为个例的样本所做出的妥协，高概率不是真实的规律。
过拟合的成因与防控
过拟合的主要原因有以下两点：
情况1：训练数据存在噪音，导致模型学到了噪音，而不是真实规律。
情况2：使用强大模型（表示空间大）的同时训练数据太少，导致在训练数据上表现良好的候选假设太多，锁定了一个“虚假正确”的假设。
对于情况1，我们使用数据清洗和修正来解决。 对于情况2，我们或者限制模型表示能力，或者收集更多的训练数据。
而清洗训练数据中的错误，或收集更多的训练数据往往是一句“正确的废话”，在任何时候我们都想获得更多更高质量的数据。在实际项目中，更快、更低成本可控制过拟合的方法，只有限制模型的表示能力。
正则化项
为了防止模型过拟合，在没有扩充样本量的可能下，只能降低模型的复杂度，可以通过限制参数的数量或可能取值（参数值尽量小）实现。
具体来说，在模型的优化目标（损失）中人为加入对参数规模的惩罚项。当参数越多或取值越大时，该惩罚项就越大。通过调整惩罚项的权重系数，可以使模型在“尽量减少训练损失”和“保持模型的泛化能力”之间取得平衡。泛化能力表示模型在没有见过的样本上依然有效。正则化项的存在，增加了模型在训练集上的损失。
飞桨支持为所有参数加上统一的正则化项，也支持为特定的参数添加正则化项。前者的实现如下代码所示，仅在优化器中设置regularization参数即可实现。使用参数regularization_coeff调节正则化项的权重，权重越大时，对模型复杂度的惩罚越高。
with fluid.dygraph.guard():
model = MNIST()
model.train()
#各种优化算法均可以加入正则化项，避免过拟合，参数regularization_coeff调节正则化项的权重
#optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.01, regularization=fluid.regularizer.L2Decay(regularization_coeff=0.1),parameter_list=model.parameters()))
optimizer = fluid.optimizer.AdamOptimizer(learning_rate=0.01, regularization=fluid.regularizer.L2Decay(regularization_coeff=0.1),parameter_list=model.parameters())
EPOCH_NUM = 10
for epoch_id in range(EPOCH_NUM):
for batch_id, data in enumerate(train_loader()):
#准备数据，变得更加简洁
image_data, label_data = data
image = fluid.dygraph.to_variable(image_data)
label = fluid.dygraph.to_variable(label_data)
#前向计算的过程，同时拿到模型输出值和分类准确率
predict, acc = model(image, label)
#计算损失，取一个批次样本损失的平均值
loss = fluid.layers.cross_entropy(predict, label)
avg_loss = fluid.layers.mean(loss)
#每训练了100批次的数据，打印下当前Loss的情况
if batch_id % 100 == 0:
print("epoch: {}, batch: {}, loss is: {}, acc is {}".format(epoch_id, batch_id, avg_loss.numpy(), acc.numpy()))
#后向传播，更新参数的过程
avg_loss.backward()
optimizer.minimize(avg_loss)
model.clear_gradients()
#保存模型参数
fluid.save_dygraph(model.state_dict(), 'mnist')
可视化分析
训练模型时，经常需要观察模型的评价指标，分析模型的优化过程，以确保训练是有效的。可选用这两种工具：Matplotlib库和VisualDL。
- Matplotlib库：Matplotlib库是Python中使用的最多的2D图形绘图库，它有一套完全仿照MATLAB的函数形式的绘图接口，使用轻量级的PLT库（Matplotlib）作图是非常简单的。
- VisualDL：如果期望使用更加专业的作图工具，可以尝试VisualDL，飞桨可视化分析工具。VisualDL能够有效地展示飞桨在运行过程中的计算图、各种指标变化趋势和数据信息。
使用Matplotlib库绘制损失随训练下降的曲线图
将训练的批次编号作为X轴坐标，该批次的训练损失作为Y轴坐标。
-
训练开始前，声明两个列表变量存储对应的批次编号(iters=[])和训练损失(losses=[])。
-
随着训练的进行，将iter和losses两个列表填满。
-
训练结束后，将两份数据以参数形式导入PLT的横纵坐标。
-
最后，调用plt.plot()函数即可完成作图。
具体代码如下：
#引入matplotlib库
import matplotlib.pyplot as plt
with fluid.dygraph.guard(place):
model = MNIST()
model.train()
optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.01, parameter_list=model.parameters())
EPOCH_NUM = 10
iter=0
iters=[]
losses=[]
for epoch_id in range(EPOCH_NUM):
for batch_id, data in enumerate(train_loader()):
#准备数据，变得更加简洁
image_data, label_data = data
image = fluid.dygraph.to_variable(image_data)
label = fluid.dygraph.to_variable(label_data)
#前向计算的过程，同时拿到模型输出值和分类准确率
predict, acc = model(image, label)
#计算损失，取一个批次样本损失的平均值
loss = fluid.layers.cross_entropy(predict, label)
avg_loss = fluid.layers.mean(loss)
#每训练了100批次的数据，打印下当前Loss的情况
if batch_id % 100 == 0:
print("epoch: {}, batch: {}, loss is: {}, acc is {}".format(epoch_id, batch_id, avg_loss.numpy(), acc.numpy()))
iters.append(iter)
losses.append(avg_loss.numpy())
iter = iter + 100
#后向传播，更新参数的过程
avg_loss.backward()
optimizer.minimize(avg_loss)
model.clear_gradients()
#保存模型参数
fluid.save_dygraph(model.state_dict(), 'mnist')
使用VisualDL可视化分析
飞桨可视化分析工具，以丰富的图表呈现训练参数变化趋势、模型结构、数据样本、高维数据分布等。帮助用户清晰直观地理解深度学习模型训练过程及模型结构，进而实现高效的模型调优，具体代码实现如下。
步骤1：引入VisualDL库，定义作图数据存储位置（供第3步使用），本案例的路径是“log”。
步骤2：在训练过程中插入作图语句。当每100个batch训练完成后，将当前损失作为一个新增的数据点(iter和acc的映射对)存储到第一步设置的文件中。使用变量iter记录下已经训练的批次数，作为作图的X轴坐标。
步骤3：命令行启动VisualDL。
使用“visualdl --logdir [数据文件所在文件夹路径] 的命令启动VisualDL。在VisualDL启动后，命令行会打印出可用浏览器查阅图形结果的网址。
步骤4：打开浏览器，查看作图结果。
具体代码如下：
#引入VisualDL库，并设定保存作图数据的文件位置
from visualdl import LogWriter
log_writer = LogWriter(logdir="./log")
with fluid.dygraph.guard():
model = MNIST()
model.train()
optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.01, parameter_list=model.parameters())
EPOCH_NUM = 10
iter = 0
for epoch_id in range(EPOCH_NUM):
for batch_id, data in enumerate(train_loader()):
#准备数据，变得更加简洁
image_data, label_data = data
image = fluid.dygraph.to_variable(image_data)
label = fluid.dygraph.to_variable(label_data)
#前向计算的过程，同时拿到模型输出值和分类准确率
predict, avg_acc = model(image, label)
#计算损失，取一个批次样本损失的平均值
loss = fluid.layers.cross_entropy(predict, label)
avg_loss = fluid.layers.mean(loss)
#每训练了100批次的数据，打印下当前Loss的情况
if batch_id % 100 == 0:
print("epoch: {}, batch: {}, loss is: {}, acc is {}".format(epoch_id, batch_id, avg_loss.numpy(), avg_acc.numpy()))
log_writer.add_scalar(tag = 'acc', step = iter, value = avg_acc.numpy())
log_writer.add_scalar(tag = 'loss', step = iter, value = avg_loss.numpy())
iter = iter + 100
#后向传播，更新参数的过程
avg_loss.backward()
optimizer.minimize(avg_loss)
model.clear_gradients()
#保存模型参数
fluid.save_dygraph(model.state_dict(), 'mnist')
STEP 5 模型保存
模型加载及恢复训练
在我们训练模型的时候，总会有一些不固定因素可能导致程序中断，所以保存数据尤为重要。下面介绍一下飞桨恢复训练的实现方法。
首先是我们原有的网络定义部分。
import os
import random
import paddle
import paddle.fluid as fluid
from paddle.fluid.dygraph.nn import Conv2D, Pool2D, Linear
import numpy as np
from PIL import Image
import gzip
import json
# 定义数据集读取器
def load_data(mode='train'):
# 数据文件
datafile = './work/mnist.json.gz'
print('loading mnist dataset from {} ......'.format(datafile))
data = json.load(gzip.open(datafile))
train_set, val_set, eval_set = data
# 数据集相关参数，图片高度IMG_ROWS, 图片宽度IMG_COLS
IMG_ROWS = 28
IMG_COLS = 28
if mode == 'train':
imgs = train_set[0]
labels = train_set[1]
elif mode == 'valid':
imgs = val_set[0]
labels = val_set[1]
elif mode == 'eval':
imgs = eval_set[0]
labels = eval_set[1]
imgs_length = len(imgs)
assert len(imgs) == len(labels), \
"length of train_imgs({}) should be the same as train_labels({})".format(
len(imgs), len(labels))
index_list = list(range(imgs_length))
# 读入数据时用到的batchsize
BATCHSIZE = 100
# 定义数据生成器
def data_generator():
if mode == 'train':
random.shuffle(index_list)
imgs_list = []
labels_list = []
for i in index_list:
img = np.reshape(imgs[i], [1, IMG_ROWS, IMG_COLS]).astype('float32')
label = np.reshape(labels[i], [1]).astype('int64')
imgs_list.append(img)
labels_list.append(label)
if len(imgs_list) == BATCHSIZE:
yield np.array(imgs_list), np.array(labels_list)
imgs_list = []
labels_list = []
# 如果剩余数据的数目小于BATCHSIZE，
# 则剩余数据一起构成一个大小为len(imgs_list)的mini-batch
if len(imgs_list) > 0:
yield np.array(imgs_list), np.array(labels_list)
return data_generator
#调用加载数据的函数
train_loader = load_data('train')
# 定义模型结构
class MNIST(fluid.dygraph.Layer):
def __init__(self):
super(MNIST, self).__init__()
# 定义一个卷积层，使用relu激活函数
self.conv1 = Conv2D(num_channels=1, num_filters=20, filter_size=5, stride=1, padding=2, act='relu')
# 定义一个池化层，池化核为2，步长为2，使用最大池化方式
self.pool1 = Pool2D(pool_size=2, pool_stride=2, pool_type='max')
# 定义一个卷积层，使用relu激活函数
self.conv2 = Conv2D(num_channels=20, num_filters=20, filter_size=5, stride=1, padding=2, act='relu')
# 定义一个池化层，池化核为2，步长为2，使用最大池化方式
self.pool2 = Pool2D(pool_size=2, pool_stride=2, pool_type='max')
# 定义一个全连接层，输出节点数为10
self.fc = Linear(input_dim=980, output_dim=10, act='softmax')
# 定义网络的前向计算过程
def forward(self, inputs, label):
x = self.conv1(inputs)
x = self.pool1(x)
x = self.conv2(x)
x = self.pool2(x)
x = fluid.layers.reshape(x, [x.shape[0], 980])
x = self.fc(x)
if label is not None:
acc = fluid.layers.accuracy(input=x, label=label)
return x, acc
else:
return x
在开始介绍使用飞桨恢复训练前，先正常训练一个模型，优化器使用Adam，使用动态变化的学习率，学习率从0.01衰减到0.001。每训练一轮后保存一次模型，之后将采用其中某一轮的模型参数进行恢复训练，验证一次性训练和中断再恢复训练的模型表现是否一致（训练loss的变化）。
注意进行恢复训练的程序不仅要保存模型参数，还要保存优化器参数。这是因为某些优化器含有一些随着训练过程变换的参数，例如Adam, AdaGrad等优化器采用可变学习率的策略，随着训练进行会逐渐减少学习率。这些优化器的参数对于恢复训练至关重要。
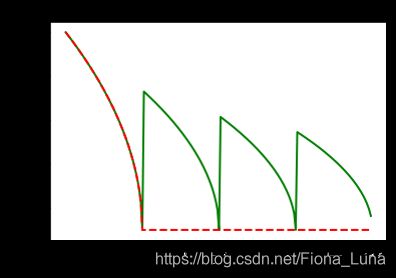
为了演示这个特性,下面训练程序使用Adam优化器，学习率以多项式曲线从0.01衰减到0.001（polynomial decay）。
lr = fluid.dygraph.PolynomialDecay(0.01, total_steps, 0.001)
learning_rate：初始学习率
decay_steps：衰减步数
end_learning_rate：最终学习率
power：多项式的幂，默认值为1.0
cycle：下降后是否重新上升，polynomial decay的变化曲线下图所示。
#在使用GPU机器时，可以将use_gpu变量设置成True
use_gpu = False
place = fluid.CUDAPlace(0) if use_gpu else fluid.CPUPlace()
with fluid.dygraph.guard(place):
model = MNIST()
model.train()
EPOCH_NUM = 5
BATCH_SIZE = 100
# 定义学习率，并加载优化器参数到模型中
total_steps = (int(60000//BATCH_SIZE) + 1) * EPOCH_NUM
lr = fluid.dygraph.PolynomialDecay(0.01, total_steps, 0.001)
# 使用Adam优化器
optimizer = fluid.optimizer.AdamOptimizer(learning_rate=lr, parameter_list=model.parameters())
for epoch_id in range(EPOCH_NUM):
for batch_id, data in enumerate(train_loader()):
#准备数据，变得更加简洁
image_data, label_data = data
image = fluid.dygraph.to_variable(image_data)
label = fluid.dygraph.to_variable(label_data)
#前向计算的过程，同时拿到模型输出值和分类准确率
predict, acc = model(image, label)
avg_acc = fluid.layers.mean(acc)
#计算损失，取一个批次样本损失的平均值
loss = fluid.layers.cross_entropy(predict, label)
avg_loss = fluid.layers.mean(loss)
#每训练了200批次的数据，打印下当前Loss的情况
if batch_id % 200 == 0:
print("epoch: {}, batch: {}, loss is: {}, acc is {}".format(epoch_id, batch_id, avg_loss.numpy(),avg_acc.numpy()))
#后向传播，更新参数的过程
avg_loss.backward()
optimizer.minimize(avg_loss)
model.clear_gradients()
# 保存模型参数和优化器的参数
fluid.save_dygraph(model.state_dict(), './checkpoint/mnist_epoch{}'.format(epoch_id))
fluid.save_dygraph(optimizer.state_dict(), './checkpoint/mnist_epoch{}'.format(epoch_id))
恢复训练
在上述训练代码中，我们训练了五轮（epoch）。在每轮结束时，均保存了模型参数和优化器相关的参数。
- 使用model.state_dict()获取模型参数。
- 使用optimizer.state_dict()获取优化器和学习率相关的参数。
- 调用fluid.save_dygraph()将参数保存到本地。
比如第一轮训练保存的文件是mnist_epoch0.pdparams，mnist_epoch0.pdopt，分别存储了模型参数和优化器参数。
当加载模型时，如果模型参数文件和优化器参数文件是相同的，我们可以使用load_dygraph同时加载这两个文件，如下代码所示。
params_dict, opt_dict = fluid.load_dygraph(params_path)
如果模型参数文件和优化器参数文件的名字不同，需要调用两次load_dygraph分别获得模型参数和优化器参数。
如何判断模型是否准确的恢复训练呢？
理想的恢复训练是模型状态回到训练中断的时刻，恢复训练之后的梯度更新走向是和恢复训练前的梯度走向完全相同的。基于此，我们可以通过恢复训练后的损失变化，判断上述方法是否能准确的恢复训练。即从epoch 0结束时保存的模型参数和优化器状态恢复训练，校验其后训练的损失变化（epoch 1）是否和不中断时的训练完全一致。
下面的代码将展示恢复训练的过程，并验证恢复训练是否成功。其中，我们重新定义一个train_again()训练函数，加载模型参数并从第一个epoch开始训练，以便读者可以校验恢复训练后的损失变化。
params_path = "./checkpoint/mnist_epoch0"
#在使用GPU机器时，可以将use_gpu变量设置成True
use_gpu = False
place = fluid.CUDAPlace(0) if use_gpu else fluid.CPUPlace()
with fluid.dygraph.guard(place):
# 加载模型参数到模型中
params_dict, opt_dict = fluid.load_dygraph(params_path)
model = MNIST()
model.load_dict(params_dict)
EPOCH_NUM = 5
BATCH_SIZE = 100
# 定义学习率，并加载优化器参数到模型中
total_steps = (int(60000//BATCH_SIZE) + 1) * EPOCH_NUM
lr = fluid.dygraph.PolynomialDecay(0.01, total_steps, 0.001)
# 使用Adam优化器
optimizer = fluid.optimizer.AdamOptimizer(learning_rate=lr, parameter_list=model.parameters())
optimizer.set_dict(opt_dict)
for epoch_id in range(1, EPOCH_NUM):
for batch_id, data in enumerate(train_loader()):
#准备数据，变得更加简洁
image_data, label_data = data
image = fluid.dygraph.to_variable(image_data)
label = fluid.dygraph.to_variable(label_data)
#前向计算的过程，同时拿到模型输出值和分类准确率
predict, acc = model(image, label)
avg_acc = fluid.layers.mean(acc)
#计算损失，取一个批次样本损失的平均值
loss = fluid.layers.cross_entropy(predict, label)
avg_loss = fluid.layers.mean(loss)
#每训练了200批次的数据，打印下当前Loss的情况
if batch_id % 200 == 0:
print("epoch: {}, batch: {}, loss is: {}, acc is {}".format(epoch_id, batch_id, avg_loss.numpy(),avg_acc.numpy()))
#后向传播，更新参数的过程
avg_loss.backward()
optimizer.minimize(avg_loss)
model.clear_gradients()
从恢复训练的损失变化来看，加载模型参数继续训练的损失函数值和正常训练损失函数值是完全一致的，可见使用飞桨实现恢复训练是极其简单的。
第三章 卷积神经网络基础
计算机视觉
计算机视觉作为一门让机器学会如何去“看”的科学学科，具体的说，就是让机器去识别摄像机拍摄的图片或视频中的物体，检测出物体所在的位置，并对目标物体进行跟踪，从而理解并描述出图片或视频里的场景和故事，以此来模拟人脑视觉系统。因此，计算机视觉也通常被叫做机器视觉，其目的是建立能够从图像或者视频中“感知”信息的人工系统。
计算机视觉技术经过几十年的发展，已经在交通（车牌识别、道路违章抓拍）、安防（人脸闸机、小区监控）、金融（刷脸支付、柜台的自动票据识别）、医疗（医疗影像诊断）、工业生产（产品缺陷自动检测）等多个领域应用，影响或正在改变人们的日常生活和工业生产方式。未来，随着技术的不断演进，必将涌现出更多的产品应用，为我们的生活创造更大的便利和更广阔的机会。
这次课程重点介绍计算机视觉的经典模型（卷积神经网络）和两个典型任务（图像分类和目标检测）。主要涵盖如下内容：
-
卷积神经网络：卷积神经网络（Convolutional Neural Networks, CNN）是计算机视觉技术最经典的模型结构。本教程主要介绍卷积神经网络的常用模块，包括：卷积、池化、激活函数、批归一化、Dropout等。
-
图像分类：介绍图像分类算法的经典模型结构，包括：LeNet、AlexNet、VGG、GoogLeNet、ResNet，并通过眼疾筛查的案例展示算法的应用。
-
目标检测：介绍目标检测YOLO-V3算法，并通过林业病虫害检测案例展示YOLO-V3算法的应用。
卷积神经网络
卷积神经网络是目前计算机视觉中使用最普遍的模型结构。本章节主要为读者介绍卷积神经网络的一些基础模块，包括：
- 卷积（Convolution）
- 池化（Pooling）
- ReLU激活函数
- 批归一化（Batch Normalization）
- 丢弃法（Dropout）
回顾一下，在上一章“一个案例带你吃透深度学习”中，我们介绍了手写数字识别任务，应用的是全连接层的特征提取，即将一张图片上的所有像素点展开成一个1维向量输入网络，存在如下两个问题：
-
输入数据的空间信息被丢失。 空间上相邻的像素点往往具有相似的RGB值，RGB的各个通道之间的数据通常密切相关，但是转化成1维向量时，这些信息被丢失。同时，图像数据的形状信息中，可能隐藏着某种本质的模式，但是转变成1维向量输入全连接神经网络时，这些模式也会被忽略。
-
模型参数过多，容易发生过拟合。 在手写数字识别案例中，每个像素点都要跟所有输出的神经元相连接。当图片尺寸变大时，输入神经元的个数会按图片尺寸的平方增大，导致模型参数过多，容易发生过拟合。
为了解决上述问题，我们引入卷积神经网络进行特征提取，既能提取到相邻像素点之间的特征模式，又能保证参数的个数不随图片尺寸变化。图6 是一个典型的卷积神经网络结构，多层卷积和池化层组合作用在输入图片上，在网络的最后通常会加入一系列全连接层，ReLU激活函数一般加在卷积或者全连接层的输出上，网络中通常还会加入Dropout来防止过拟合。
卷积（Convolution）
这一小节将为读者介绍卷积算法的原理和实现方案，并通过具体的案例展示如何使用卷积对图片进行操作，主要涵盖如下内容：
-
卷积计算
-
填充（padding）
-
步幅（stride）
-
感受野（Receptive Field）
-
多输入通道、多输出通道和批量操作
-
飞桨卷积API介绍
1) 卷积计算
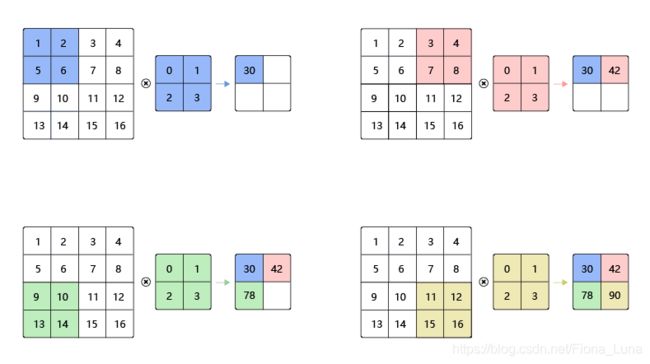
卷积是数学分析中的一种积分变换的方法，在图像处理中采用的是卷积的离散形式。这里需要说明的是，在卷积神经网络中，卷积层的实现方式实际上是数学中定义的互相关 （cross-correlation）运算，与数学分析中的卷积定义有所不同，这里跟其他框架和卷积神经网络的教程保持一致，都使用互相关运算作为卷积的定义，具体的计算过程如图7所示。
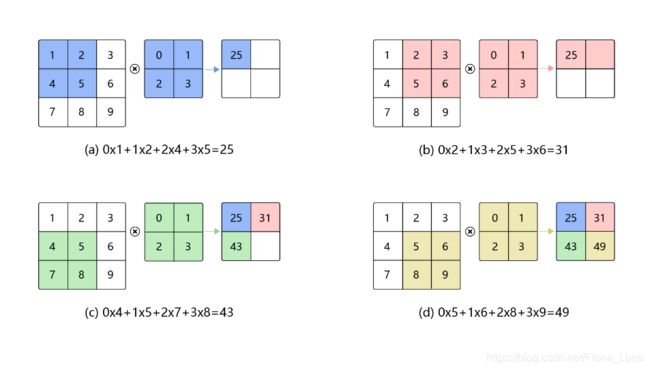
2）填充（padding）
在上面的例子中，输入图片尺寸为3×3，输出图片尺寸为2×2，经过一次卷积之后，图片尺寸变小。卷积输出特征图的尺寸计算方法如下：
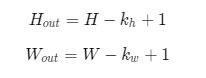
如果输入尺寸为4，卷积核大小为3时，输出尺寸为4−3+1=24-3+1=24−3+1=2。读者可以自行检查当输入图片和卷积核为其他尺寸时，上述计算式是否成立。通过多次计算我们发现，当卷积核尺寸大于1时，输出特征图的尺寸会小于输入图片尺寸。说明经过多次卷积之后尺寸会不断减小。为了避免卷积之后图片尺寸变小，通常会在图片的外围进行填充(padding)，如图所示。
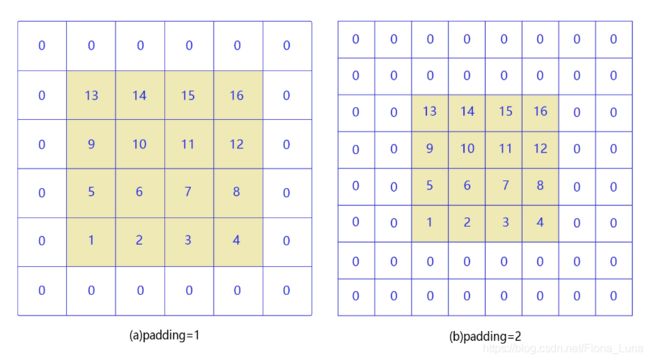
如图（a）所示：填充的大小为1，填充值为0。填充之后，输入图片尺寸从4×4变成了6×6，使用3×33的卷积核，输出图片尺寸为4×4。
如图（b）所示：填充的大小为2，填充值为0。填充之后，输入图片尺寸从4×4变成了8×8，使用3×3的卷积核，输出图片尺寸为6×6。
如果在图片高度方向，在第一行之前填充ph1行，在最后一行之后填充ph2行；在图片的宽度方向，在第1列之前填充pw1列，在最后1列之后填充pw2列；则填充之后的图片尺寸为(H+ph1+ph2)×(W+pw1+pw2)。经过大小为kh×kw的卷积核操作之后，输出图片的尺寸为：
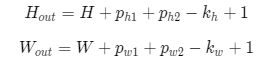
在卷积计算过程中，通常会在高度或者宽度的两侧采取等量填充，即ph1=ph2=ph, pw1=pw2=pw，上面计算公式也就变为：
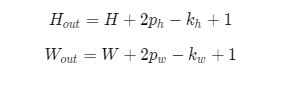
卷积核大小通常使用1，3，5，7这样的奇数，如果使用的填充大小为ph=(kh−1)/2,pw=(kw−1)/2，则卷积之后图像尺寸不变。例如当卷积核大小为3时，padding大小为1，卷积之后图像尺寸不变；同理，如果卷积核大小为5，使用padding的大小为2，也能保持图像尺寸不变。
3）步幅（stride）
上图中卷积核每次滑动一个像素点，这是步幅为1的特殊情况。
下图是步幅为2的卷积过程，卷积核在图片上移动时，每次移动大小为2个像素点。
当宽和高方向的步幅分别为sh和sw输出特征图尺寸的计算公式是：
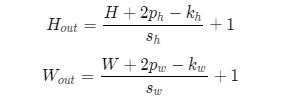
假设输入图片尺寸是H×W=100×100，卷积核大小kh×kw=3×3，填充ph=pw=1，步幅为sh=sw=2，则输出特征图的尺寸为：
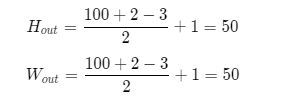
4）感受野（Receptive Field）
输出特征图上每个点的数值，是由输入图片上大小为kh×kw 的区域的元素与卷积核每个元素相乘再相加得到的，所以输入图像上kh×kw区域内每个元素数值的改变，都会影响输出点的像素值。我们将这个区域叫做输出特征图上对应点的感受野。感受野内每个元素数值的变动，都会影响输出点的数值变化。比如3×3卷积对应的感受野大小就是3×3。
5）多输入通道、多输出通道和批量操作
前面介绍的卷积计算过程比较简单，实际应用时，处理的问题要复杂的多。例如：对于彩色图片有RGB三个通道，需要处理多输入通道的场景。输出特征图往往也会具有多个通道，而且在神经网络的计算中常常是把一个批次的样本放在一起计算，所以卷积算子需要具有批量处理多输入和多输出通道数据的功能，下面将分别介绍这几种场景的操作方式。
多输入通道场景
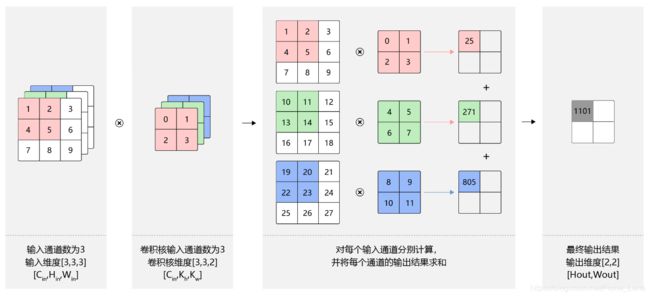
上面的例子中，卷积层的数据是一个2维数组，但实际上一张图片往往含有RGB三个通道，要计算卷积的输出结果，卷积核的形式也会发生变化。假设输入图片的通道数为Cin，输入数据的形状是Cin×Hin×Win ，计算过程如图所示。
多输出通道场景
一般来说，卷积操作的输出特征图也会具有多个通道Cout，这时我们需要设计Cout个维度为Cin×kh×kw的卷积核，卷积核数组的维度是Cout×Cin×kh×kw，如图所示。
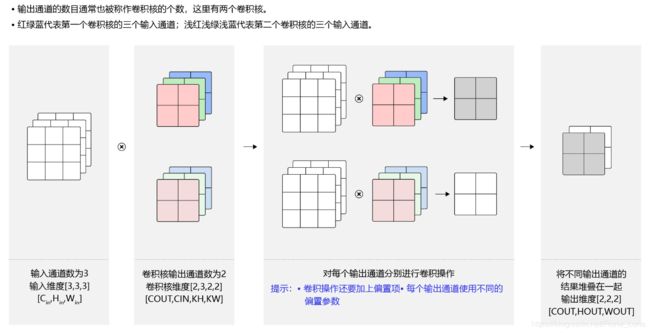
批量操作
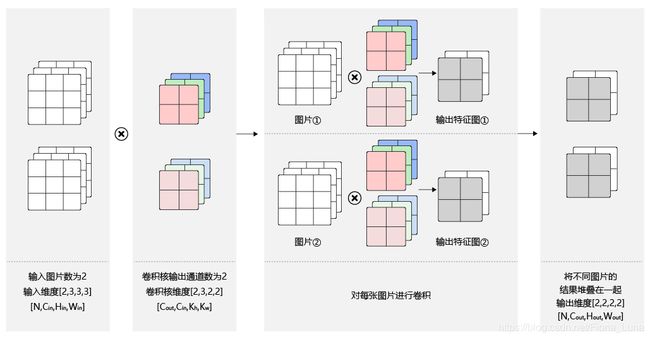
在卷积神经网络的计算中，通常将多个样本放在一起形成一个mini-batch进行批量操作，即输入数据的维度是N×Cin×Hin×Win。由于会对每张图片使用同样的卷积核进行卷积操作，卷积核的维度与上面多输出通道的情况一样，仍然是Cout×Cin×kh×kw ，输出特征图的维度是N×Cout×Hout×Wout，如图 所示。
6）飞桨卷积API介绍
飞桨卷积算子对应的API是paddle.fluid.dygraph.Conv2D，用户可以直接调用API进行计算，也可以在此基础上修改。常用的参数如下：
- num_channels (int) - 输入图像的通道数。
- num_fliters (int) - 卷积核的个数，和输出特征图通道数相同，相当于上文中的Cout 。
- filter_size(int|tuple) - 卷积核大小，可以是整数，比如3，表示卷积核的高和宽均为3 ；或者是两个整数的list，例如[3,2]，表示卷积核的高为3，宽为2。
- stride(int|tuple) - 步幅，可以是整数，默认值为1，表示垂直和水平滑动步幅均为1；或者是两个整数的list，例如[3,2]，表示垂直滑动步幅为3，水平滑动步幅为2。
- padding(int|tuple) - 填充大小，可以是整数，比如1，表示竖直和水平边界填充大小均为1；或者是两个整数的list，例如[2,1]，表示竖直边界填充大小为2，水平边界填充大小为1。
- act（str）- 应用于输出上的激活函数，如Tanh、Softmax、Sigmoid，Relu等，默认值为None。
池化（Pooling）
池化是使用某一位置的相邻输出的总体统计特征代替网络在该位置的输出，其好处是当输入数据做出少量平移时，经过池化函数后的大多数输出还能保持不变。比如：当识别一张图像是否是人脸时，我们需要知道人脸左边有一只眼睛，右边也有一只眼睛，而不需要知道眼睛的精确位置，这时候通过池化某一片区域的像素点来得到总体统计特征会显得很有用。由于池化之后特征图会变得更小，如果后面连接的是全连接层，能有效的减小神经元的个数，节省存储空间并提高计算效率。 如图所示，将一个2×2的区域池化成一个像素点。通常有两种方法，平均池化和最大池化。
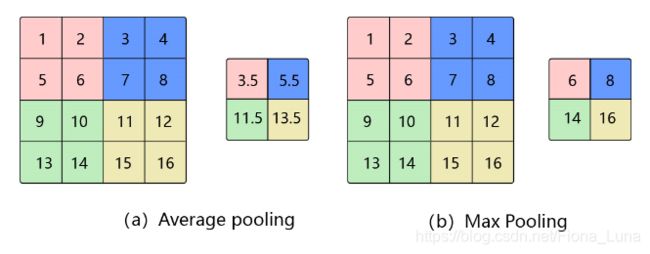
如图（a）：平均池化。这里使用大小为2×22\times22×2的池化窗口，每次移动的步幅为2，对池化窗口覆盖区域内的像素取平均值，得到相应的输出特征图的像素值。
如图（b）：最大池化。对池化窗口覆盖区域内的像素取最大值，得到输出特征图的像素值。当池化窗口在图片上滑动时，会得到整张输出特征图。池化窗口的大小称为池化大小，用kh×kw表示。在卷积神经网络中用的比较多的是窗口大小为2×2，步幅为2的池化。
与卷积核类似，池化窗口在图片上滑动时，每次移动的步长称为步幅，当宽和高方向的移动大小不一样时，分别用sw和sh表示。也可以对需要进行池化的图片进行填充，填充方式与卷积类似，假设在第一行之前填充ph1行，在最后一行后面填充ph2行。在第一列之前填充pw1列，在最后一列之后填充pw2列，则池化层的输出特征图大小为：
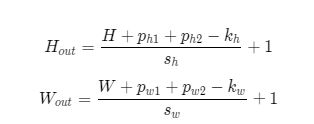
在卷积神经网络中，通常使用2×2大小的池化窗口，步幅也使用2，填充为0，则输出特征图的尺寸为：
通过这种方式的池化，输出特征图的高和宽都减半，但通道数不会改变。
ReLU激活函数
前面介绍的网络结构中，普遍使用Sigmoid函数做激活函数。在神经网络发展的早期，Sigmoid函数用的比较多，而目前用的较多的激活函数是ReLU。这是因为Sigmoid函数在反向传播过程中，容易造成梯度的衰减。让我们仔细观察Sigmoid函数的形式，就能发现这一问题。
Sigmoid激活函数定义如下：
ReLU激活函数的定义如下：
批归一化（Batch Normalization）
批归一化方法方法（Batch Normalization，BatchNorm）是由Ioffe和Szegedy于2015年提出的，已被广泛应用在深度学习中，其目的是对神经网络中间层的输出进行标准化处理，使得中间层的输出更加稳定。
通常我们会对神经网络的数据进行标准化处理，处理后的样本数据集满足均值为0，方差为1的统计分布，这是因为当输入数据的分布比较固定时，有利于算法的稳定和收敛。对于深度神经网络来说，由于参数是不断更新的，即使输入数据已经做过标准化处理，但是对于比较靠后的那些层，其接收到的输入仍然是剧烈变化的，通常会导致数值不稳定，模型很难收敛。BatchNorm能够使神经网络中间层的输出变得更加稳定，并有如下三个优点：
-
使学习快速进行（能够使用较大的学习率）
-
降低模型对初始值的敏感性
-
从一定程度上抑制过拟合
BatchNorm主要思路是在训练时按mini-batch为单位，对神经元的数值进行归一化，使数据的分布满足均值为0，方差为1。具体计算过程如下： -
计算mini-batch内样本的均值
-
计算mini-batch内样本的方差
-
计算标准化之后的输出
丢弃法（Dropout）
丢弃法（Dropout）是深度学习中一种常用的抑制过拟合的方法，其做法是在神经网络学习过程中，随机删除一部分神经元。训练时，随机选出一部分神经元，将其输出设置为0，这些神经元将不对外传递信号。
下图是Dropout示意图，左边是完整的神经网络，右边是应用了Dropout之后的网络结构。应用Dropout之后，会将标了×\times×的神经元从网络中删除，让它们不向后面的层传递信号。在学习过程中，丢弃哪些神经元是随机决定，因此模型不会过度依赖某些神经元，能一定程度上抑制过拟合。
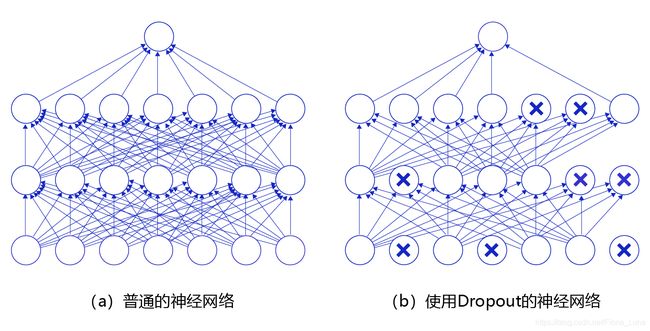
在预测场景时，会向前传递所有神经元的信号，可能会引出一个新的问题：训练时由于部分神经元被随机丢弃了，输出数据的总大小会变小。比如：计算其L1L1L1范数会比不使用Dropout时变小，但是预测时却没有丢弃神经元，这将导致训练和预测时数据的分布不一样。为了解决这个问题，飞桨支持如下两种方法：
downgrade_in_infer
训练时以比例rrr随机丢弃一部分神经元，不向后传递它们的信号；预测时向后传递所有神经元的信号，但是将每个神经元上的数值乘以 (1−r)。
upscale_in_train
训练时以比例rrr随机丢弃一部分神经元，不向后传递它们的信号，但是将那些被保留的神经元上的数值除以 (1−r)；预测时向后传递所有神经元的信号，不做任何处理。
在飞桨dropout API中，paddle.fluid.layers.dropout通过dropout_implementation参数来指定用哪种方式对神经元进行操作，dropout_implementation参数的可选值是’downgrade_in_infer’或’upscale_in_train’，缺省值是’downgrade_in_infer’。
图像分类
图像分类是根据图像的语义信息对不同类别图像进行区分，是计算机视觉的核心，是物体检测、图像分割、物体跟踪、行为分析、人脸识别等其他高层次视觉任务的基础。图像分类在许多领域都有着广泛的应用，如：安防领域的人脸识别和智能视频分析等，交通领域的交通场景识别，互联网领域基于内容的图像检索和相册自动归类，医学领域的图像识别等。
课程基于眼疾分类数据集iChallenge-PM，对图像分类领域的经典卷积神经网络进行剖析，介绍如何应用这些基础模块构建卷积神经网络，解决图像分类问题。涵盖如下卷积神经网络：
-
LeNet：Yan LeCun等人于1998年第一次将卷积神经网络应用到图像分类任务上[1]，在手写数字识别任务上取得了巨大成功。
-
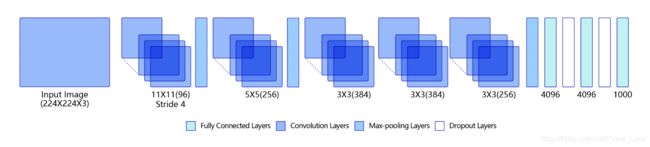
AlexNet：Alex Krizhevsky等人在2012年提出了AlexNet[2], 并应用在大尺寸图片数据集ImageNet上，获得了2012年ImageNet比赛冠军(ImageNet Large Scale Visual Recognition Challenge，ILSVRC）。
-
VGG：Simonyan和Zisserman于2014年提出了VGG网络结构[3]，是当前最流行的卷积神经网络之一，由于其结构简单、应用性极强而深受广大研究者欢迎。
-
GoogLeNet：Christian Szegedy等人在2014提出了GoogLeNet[4]，并取得了2014年ImageNet比赛冠军。
-
ResNet：Kaiming He等人在2015年提出了ResNet[5]，通过引入残差模块加深网络层数，在ImagNet数据集上的错误率降低到3.6%，超越了人眼识别水平。ResNet的设计思想深刻地影响了后来的深度神经网络的设计。
LeNet
LeNet是最早的卷积神经网络之一[1]。1998年，Yan LeCun第一次将LeNet卷积神经网络应用到图像分类上，在手写数字识别任务中取得了巨大成功。LeNet通过连续使用卷积和池化层的组合提取图像特征，其架构如图所示，这里展示的是作者论文中的LeNet-5模型：
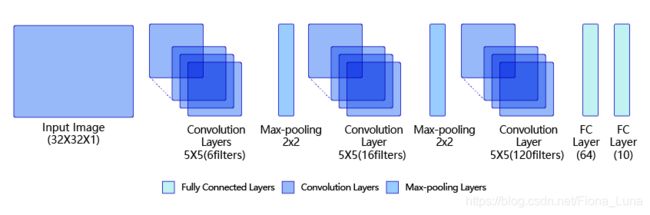
第一模块：包含5×5的6通道卷积和2×2的池化。卷积提取图像中包含的特征模式（激活函数使用sigmoid），图像尺寸从32减小到28。经过池化层可以降低输出特征图对空间位置的敏感性，图像尺寸减到14。
第二模块：和第一模块尺寸相同，通道数由6增加为16。卷积操作使图像尺寸减小到10，经过池化后变成5。
第三模块：包含5×5的120通道卷积。卷积之后的图像尺寸减小到1，但是通道数增加为120。将经过第3次卷积提取到的特征图输入到全连接层。第一个全连接层的输出神经元的个数是64，第二个全连接层的输出神经元个数是分类标签的类别数，对于手写数字识别其大小是10。然后使用Softmax激活函数即可计算出每个类别的预测概率。
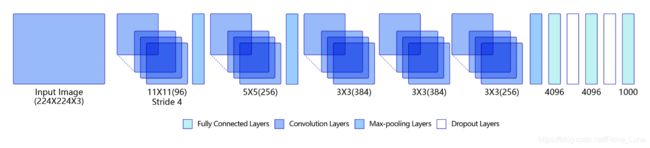
AlexNet
虽然LeNet在手写数字识别数据集上取得了很好的结果，但在更大的数据集上表现却并不好。自从1998年LeNet问世以来，接下来十几年的时间里，神经网络并没有在计算机视觉领域取得很好的结果，反而一度被其它算法所超越，原因主要有两方面，一是神经网络的计算比较复杂，对当时计算机的算力来说，训练神经网络是件非常耗时的事情；另一方面，当时还没有专门针对神经网络做算法和训练技巧的优化，神经网络的收敛是件非常困难的事情。
随着技术的进步和发展，计算机的算力越来越强大，尤其是在GPU并行计算能力的推动下，复杂神经网络的计算也变得更加容易实施。另一方面，互联网上涌现出越来越多的数据，极大的丰富了数据库。同时也有越来越多的研究人员开始专门针对神经网络做算法和模型的优化，Alex Krizhevsky等人提出的AlexNet以很大优势获得了2012年ImageNet比赛的冠军。这一成果极大的激发了产业界对神经网络的兴趣，开创了使用深度神经网络解决图像问题的途径，随后也在这一领域涌现出越来越多的优秀成果。
AlexNet与LeNet相比，具有更深的网络结构，包含5层卷积和3层全连接，同时使用了如下三种方法改进模型的训练过程：
-
数据增广：深度学习中常用的一种处理方式，通过对训练随机加一些变化，比如平移、缩放、裁剪、旋转、翻转或者增减亮度等，产生一系列跟原始图片相似但又不完全相同的样本，从而扩大训练数据集。通过这种方式，可以随机改变训练样本，避免模型过度依赖于某些属性，能从一定程度上抑制过拟合。
-
使用Dropout抑制过拟合
-
使用ReLU激活函数减少梯度消失现象
AlexNet的具体结构如图所示：
VGG
VGG是当前最流行的CNN模型之一，2014年由Simonyan和Zisserman提出，其命名来源于论文作者所在的实验室Visual Geometry Group。AlexNet模型通过构造多层网络，取得了较好的效果，但是并没有给出深度神经网络设计的方向。VGG通过使用一系列大小为3x3的小尺寸卷积核和pooling层构造深度卷积神经网络，并取得了较好的效果。VGG模型因为结构简单、应用性极强而广受研究者欢迎，尤其是它的网络结构设计方法，为构建深度神经网络提供了方向。
下图是VGG-16的网络结构示意图，有13层卷积和3层全连接层。VGG网络的设计严格使用3×3的卷积层和池化层来提取特征，并在网络的最后面使用三层全连接层，将最后一层全连接层的输出作为分类的预测。 在VGG中每层卷积将使用ReLU作为激活函数，在全连接层之后添加dropout来抑制过拟合。使用小的卷积核能够有效地减少参数的个数，使得训练和测试变得更加有效。比如使用两层3×3卷积层，可以得到感受野为5的特征图，而比使用5×5的卷积层需要更少的参数。由于卷积核比较小，可以堆叠更多的卷积层，加深网络的深度，这对于图像分类任务来说是有利的。VGG模型的成功证明了增加网络的深度，可以更好的学习图像中的特征模式。
GoogLeNet
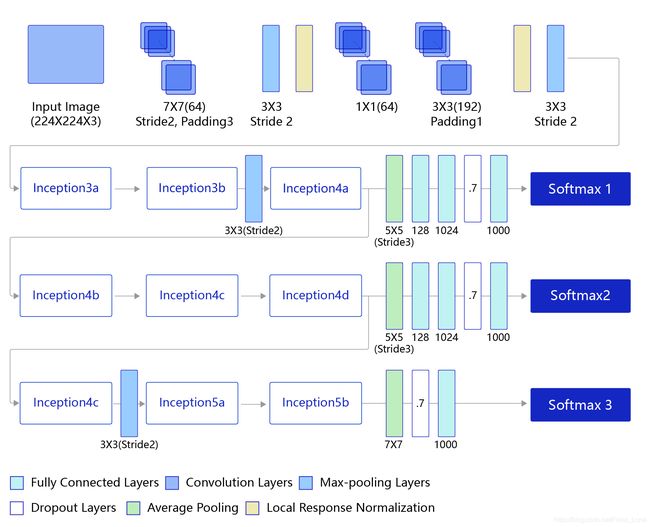
GoogLeNet是2014年ImageNet比赛的冠军，它的主要特点是网络不仅有深度，还在横向上具有“宽度”。由于图像信息在空间尺寸上的巨大差异，如何选择合适的卷积核大小来提取特征就显得比较困难了。空间分布范围更广的图像信息适合用较大的卷积核来提取其特征，而空间分布范围较小的图像信息则适合用较小的卷积核来提取其特征。为了解决这个问题，GoogLeNet提出了一种被称为Inception模块的方案。具体网络结构如图所示：
ResNet
ResNet是2015年ImageNet比赛的冠军，将识别错误率降低到了3.6%，这个结果甚至超出了正常人眼识别的精度。
通过前面几个经典模型学习，我们可以发现随着深度学习的不断发展，模型的层数越来越多，网络结构也越来越复杂。那么是否加深网络结构，就一定会得到更好的效果呢？从理论上来说，假设新增加的层都是恒等映射，只要原有的层学出跟原模型一样的参数，那么深模型结构就能达到原模型结构的效果。换句话说，原模型的解只是新模型的解的子空间，在新模型解的空间里应该能找到比原模型解对应的子空间更好的结果。但是实践表明，增加网络的层数之后，训练误差往往不降反升。
Kaiming He等人提出了残差网络ResNet来解决上述问题，其基本思想如图所示。
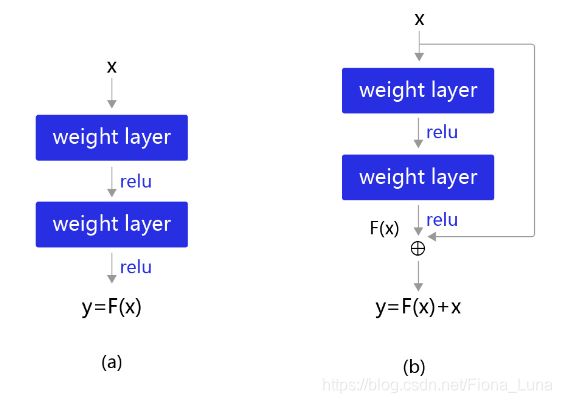
图(a)：表示增加网络的时候，将x映射成y=F(x)输出。
图(b)：对图(a)作了改进，输出y=F(x)+x。这时不是直接学习输出特征y的表示，而是学习y−x。
如果想学习出原模型的表示，只需将F(x)的参数全部设置为0，则y=x是恒等映射。
F(x)=y−x也叫做残差项，如果x→y的映射接近恒等映射，图中通过学习残差项也比图中学习完整映射形式更加容易。
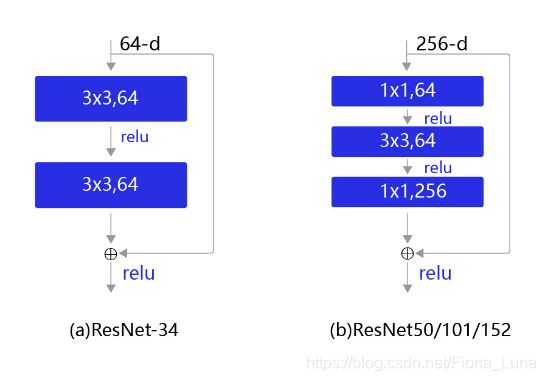
下图表示出了ResNet-50的结构，一共包含49层卷积和1层全连接，所以被称为ResNet-50。
目标检测
对计算机而言，能够“看到”的是图像被编码之后的数字，但它很难解高层语义概念，比如图像或者视频帧中出现目标的是人还是物体，更无法定位目标出现在图像中哪个区域。目标检测的主要目的是让计算机可以自动识别图片或者视频帧中所有目标的类别，并在该目标周围绘制边界框，标示出每个目标的位置，如图所示。
图（a）是图像分类任务，只需识别出这是一张斑马的图片。
图（b）是目标检测任务，不仅要识别出这是一张斑马的图片，还要标出图中斑马的位置。
目标检测基础概念
在介绍目标检测算法之前，课程先介绍一些跟检测相关的基本概念，包括边界框、锚框和交并比等。
边界框（bounding box）
检测任务需要同时预测物体的类别和位置，因此需要引入一些跟位置相关的概念。通常使用边界框（bounding box，bbox）来表示物体的位置，边界框是正好能包含物体的矩形框。
通常有两种格式来表示边界框的位置：
- xyxy，即(x1,y1,x2,y2)，其中(x1,y~1
)是矩形框左上角的坐标，(x~2~,y~2)是矩形框右下角的坐标。 - xywh，即(x,y,w,h)，其中(x,y)是矩形框中心点的坐标，w是矩形框的宽度，h是矩形框的高度。
锚框（Anchor box）
锚框与物体边界框不同，是由人们假想出来的一种框。先设定好锚框的大小和形状，再以图像上某一个点为中心画出矩形框。
在目标检测模型中，通常会以某种规则在图片上生成一系列锚框，将这些锚框当成可能的候选区域。模型对这些候选区域是否包含物体进行预测，如果包含目标物体，则还需要进一步预测出物体所属的类别。还有更为重要的一点是，由于锚框位置是固定的，它不大可能刚好跟物体边界框重合，所以需要在锚框的基础上进行微调以形成能准确描述物体位置的预测框，模型需要预测出微调的幅度。在训练过程中，模型通过学习不断的调整参数，最终能学会如何判别出锚框所代表的候选区域是否包含物体，如果包含物体的话，物体属于哪个类别，以及物体边界框相对于锚框位置需要调整的幅度。
交并比
在检测任务中是使用交并比（Intersection of Union，IoU）作为衡量指标。这一概念来源于数学中的集合，用来描述两个集合AAA和BBB之间的关系，它等于两个集合的交集里面所包含的元素个数，除以它们的并集里面所包含的元素个数，具体计算公式如下：
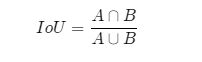
我们将用这个概念来描述两个框之间的重合度。两个框可以看成是两个像素的集合，它们的交并比等于两个框重合部分的面积除以它们合并起来的面积。
林业病虫害数据集和数据预处理方法介绍
在本次的课程中，将使用百度与林业大学合作开发的林业病虫害防治项目中用到昆虫数据集，关于该项目和数据集的更多信息，可以参考相关报道。在这一小节中将为读者介绍该数据集，以及计算机视觉任务中常用的数据预处理方法。
读取AI识虫数据集标注信息
AI识虫数据集结构如下：
- 提供了2183张图片，其中训练集1693张，验证集245，测试集245张。
- 包含7种昆虫，分别是Boerner、Leconte、Linnaeus、acuminatus、armandi、coleoptera和linnaeus。
- 包含了图片和标注，请读者先将数据解压，并存放在insects目录下。
-
INSECT_NAMES = [‘Boerner’, ‘Leconte’, ‘Linnaeus’,
‘acuminatus’, ‘armandi’, ‘coleoptera’, ‘linnaeus’]
def get_insect_names():
“”"
return a dict, as following,
{‘Boerner’: 0,
‘Leconte’: 1,
‘Linnaeus’: 2,
‘acuminatus’: 3,
‘armandi’: 4,
‘coleoptera’: 5,
‘linnaeus’: 6
}
It can map the insect name into an integer label.
“”"
insect_category2id = {}
for i, item in enumerate(INSECT_NAMES):
insect_category2id[item] = i
return insect_category2id
调用get_insect_names函数返回一个dict，其键-值对描述了昆虫名称-数字类别之间的映射关系。
下面的程序从annotations/xml目录下面读取所有文件标注信息。
```python
import os
import numpy as np
import xml.etree.ElementTree as ET
def get_annotations(cname2cid, datadir):
filenames = os.listdir(os.path.join(datadir, 'annotations', 'xmls'))
records = []
ct = 0
for fname in filenames:
fid = fname.split('.')[0]
fpath = os.path.join(datadir, 'annotations', 'xmls', fname)
img_file = os.path.join(datadir, 'images', fid + '.jpeg')
tree = ET.parse(fpath)
if tree.find('id') is None:
im_id = np.array([ct])
else:
im_id = np.array([int(tree.find('id').text)])
objs = tree.findall('object')
im_w = float(tree.find('size').find('width').text)
im_h = float(tree.find('size').find('height').text)
gt_bbox = np.zeros((len(objs), 4), dtype=np.float32)
gt_class = np.zeros((len(objs), ), dtype=np.int32)
is_crowd = np.zeros((len(objs), ), dtype=np.int32)
difficult = np.zeros((len(objs), ), dtype=np.int32)
for i, obj in enumerate(objs):
cname = obj.find('name').text
gt_class[i] = cname2cid[cname]
_difficult = int(obj.find('difficult').text)
x1 = float(obj.find('bndbox').find('xmin').text)
y1 = float(obj.find('bndbox').find('ymin').text)
x2 = float(obj.find('bndbox').find('xmax').text)
y2 = float(obj.find('bndbox').find('ymax').text)
x1 = max(0, x1)
y1 = max(0, y1)
x2 = min(im_w - 1, x2)
y2 = min(im_h - 1, y2)
# 这里使用xywh格式来表示目标物体真实框
gt_bbox[i] = [(x1+x2)/2.0 , (y1+y2)/2.0, x2-x1+1., y2-y1+1.]
is_crowd[i] = 0
difficult[i] = _difficult
voc_rec = {
'im_file': img_file,
'im_id': im_id,
'h': im_h,
'w': im_w,
'is_crowd': is_crowd,
'gt_class': gt_class,
'gt_bbox': gt_bbox,
'gt_poly': [],
'difficult': difficult
}
if len(objs) != 0:
records.append(voc_rec)
ct += 1
return records
TRAINDIR = '/home/aistudio/work/insects/train'
TESTDIR = '/home/aistudio/work/insects/test'
VALIDDIR = '/home/aistudio/work/insects/val'
cname2cid = get_insect_names()
records = get_annotations(cname2cid, TRAINDIR)
通过上面的程序，将所有训练数据集的标注数据全部读取出来了，存放在records列表下面，其中每一个元素是一张图片的标注数据，包含了图片存放地址，图片id，图片高度和宽度，图片中所包含的目标物体的种类和位置。
数据读取和预处理
数据预处理是训练神经网络时非常重要的步骤。合适的预处理方法，可以帮助模型更好的收敛并防止过拟合。首先我们需要从磁盘读入数据，然后需要对这些数据进行预处理，为了保证网络运行的速度通常还要对数据预处理进行加速。
数据读取
前面已经将图片的所有描述信息保存在records中了，其中的每一个元素包含了一张图片的描述，下面的程序展示了如何根据records里面的描述读取图片及标注。
### 数据读取
import cv2
def get_bbox(gt_bbox, gt_class):
# 对于一般的检测任务来说，一张图片上往往会有多个目标物体
# 设置参数MAX_NUM = 50， 即一张图片最多取50个真实框；如果真实
# 框的数目少于50个，则将不足部分的gt_bbox, gt_class和gt_score的各项数值全设置为0
MAX_NUM = 50
gt_bbox2 = np.zeros((MAX_NUM, 4))
gt_class2 = np.zeros((MAX_NUM,))
for i in range(len(gt_bbox)):
gt_bbox2[i, :] = gt_bbox[i, :]
gt_class2[i] = gt_class[i]
if i >= MAX_NUM:
break
return gt_bbox2, gt_class2
def get_img_data_from_file(record):
"""
record is a dict as following,
record = {
'im_file': img_file,
'im_id': im_id,
'h': im_h,
'w': im_w,
'is_crowd': is_crowd,
'gt_class': gt_class,
'gt_bbox': gt_bbox,
'gt_poly': [],
'difficult': difficult
}
"""
im_file = record['im_file']
h = record['h']
w = record['w']
is_crowd = record['is_crowd']
gt_class = record['gt_class']
gt_bbox = record['gt_bbox']
difficult = record['difficult']
img = cv2.imread(im_file)
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
# check if h and w in record equals that read from img
assert img.shape[0] == int(h), \
"image height of {} inconsistent in record({}) and img file({})".format(
im_file, h, img.shape[0])
assert img.shape[1] == int(w), \
"image width of {} inconsistent in record({}) and img file({})".format(
im_file, w, img.shape[1])
gt_boxes, gt_labels = get_bbox(gt_bbox, gt_class)
# gt_bbox 用相对值
gt_boxes[:, 0] = gt_boxes[:, 0] / float(w)
gt_boxes[:, 1] = gt_boxes[:, 1] / float(h)
gt_boxes[:, 2] = gt_boxes[:, 2] / float(w)
gt_boxes[:, 3] = gt_boxes[:, 3] / float(h)
return img, gt_boxes, gt_labels, (h, w)
get_img_data_from_file()函数可以返回图片数据的数据，它们是图像数据img, 真实框坐标gt_boxes, 真实框包含的物体类别gt_labels, 图像尺寸scales。
数据预处理
在计算机视觉中，通常会对图像做一些随机的变化，产生相似但又不完全相同的样本。主要作用是扩大训练数据集，抑制过拟合，提升模型的泛化能力。
随机改变亮暗、对比度和颜色等
import numpy as np
import cv2
from PIL import Image, ImageEnhance
import random
# 随机改变亮暗、对比度和颜色等
def random_distort(img):
# 随机改变亮度
def random_brightness(img, lower=0.5, upper=1.5):
e = np.random.uniform(lower, upper)
return ImageEnhance.Brightness(img).enhance(e)
# 随机改变对比度
def random_contrast(img, lower=0.5, upper=1.5):
e = np.random.uniform(lower, upper)
return ImageEnhance.Contrast(img).enhance(e)
# 随机改变颜色
def random_color(img, lower=0.5, upper=1.5):
e = np.random.uniform(lower, upper)
return ImageEnhance.Color(img).enhance(e)
ops = [random_brightness, random_contrast, random_color]
np.random.shuffle(ops)
img = Image.fromarray(img)
img = ops[0](img)
img = ops[1](img)
img = ops[2](img)
img = np.asarray(img)
return img
随机填充
# 随机填充
def random_expand(img,
gtboxes,
max_ratio=4.,
fill=None,
keep_ratio=True,
thresh=0.5):
if random.random() > thresh:
return img, gtboxes
if max_ratio < 1.0:
return img, gtboxes
h, w, c = img.shape
ratio_x = random.uniform(1, max_ratio)
if keep_ratio:
ratio_y = ratio_x
else:
ratio_y = random.uniform(1, max_ratio)
oh = int(h * ratio_y)
ow = int(w * ratio_x)
off_x = random.randint(0, ow - w)
off_y = random.randint(0, oh - h)
out_img = np.zeros((oh, ow, c))
if fill and len(fill) == c:
for i in range(c):
out_img[:, :, i] = fill[i] * 255.0
out_img[off_y:off_y + h, off_x:off_x + w, :] = img
gtboxes[:, 0] = ((gtboxes[:, 0] * w) + off_x) / float(ow)
gtboxes[:, 1] = ((gtboxes[:, 1] * h) + off_y) / float(oh)
gtboxes[:, 2] = gtboxes[:, 2] / ratio_x
gtboxes[:, 3] = gtboxes[:, 3] / ratio_y
return out_img.astype('uint8'), gtboxes
随机裁剪
随机裁剪之前需要先定义两个函数，multi_box_iou_xywh和box_crop这两个函数将被保存在box_utils.py文件中。
import numpy as np
def multi_box_iou_xywh(box1, box2):
"""
In this case, box1 or box2 can contain multi boxes.
Only two cases can be processed in this method:
1, box1 and box2 have the same shape, box1.shape == box2.shape
2, either box1 or box2 contains only one box, len(box1) == 1 or len(box2) == 1
If the shape of box1 and box2 does not match, and both of them contain multi boxes, it will be wrong.
"""
assert box1.shape[-1] == 4, "Box1 shape[-1] should be 4."
assert box2.shape[-1] == 4, "Box2 shape[-1] should be 4."
b1_x1, b1_x2 = box1[:, 0] - box1[:, 2] / 2, box1[:, 0] + box1[:, 2] / 2
b1_y1, b1_y2 = box1[:, 1] - box1[:, 3] / 2, box1[:, 1] + box1[:, 3] / 2
b2_x1, b2_x2 = box2[:, 0] - box2[:, 2] / 2, box2[:, 0] + box2[:, 2] / 2
b2_y1, b2_y2 = box2[:, 1] - box2[:, 3] / 2, box2[:, 1] + box2[:, 3] / 2
inter_x1 = np.maximum(b1_x1, b2_x1)
inter_x2 = np.minimum(b1_x2, b2_x2)
inter_y1 = np.maximum(b1_y1, b2_y1)
inter_y2 = np.minimum(b1_y2, b2_y2)
inter_w = inter_x2 - inter_x1
inter_h = inter_y2 - inter_y1
inter_w = np.clip(inter_w, a_min=0., a_max=None)
inter_h = np.clip(inter_h, a_min=0., a_max=None)
inter_area = inter_w * inter_h
b1_area = (b1_x2 - b1_x1) * (b1_y2 - b1_y1)
b2_area = (b2_x2 - b2_x1) * (b2_y2 - b2_y1)
return inter_area / (b1_area + b2_area - inter_area)
def box_crop(boxes, labels, crop, img_shape):
x, y, w, h = map(float, crop)
im_w, im_h = map(float, img_shape)
boxes = boxes.copy()
boxes[:, 0], boxes[:, 2] = (boxes[:, 0] - boxes[:, 2] / 2) * im_w, (
boxes[:, 0] + boxes[:, 2] / 2) * im_w
boxes[:, 1], boxes[:, 3] = (boxes[:, 1] - boxes[:, 3] / 2) * im_h, (
boxes[:, 1] + boxes[:, 3] / 2) * im_h
crop_box = np.array([x, y, x + w, y + h])
centers = (boxes[:, :2] + boxes[:, 2:]) / 2.0
mask = np.logical_and(crop_box[:2] <= centers, centers <= crop_box[2:]).all(
axis=1)
boxes[:, :2] = np.maximum(boxes[:, :2], crop_box[:2])
boxes[:, 2:] = np.minimum(boxes[:, 2:], crop_box[2:])
boxes[:, :2] -= crop_box[:2]
boxes[:, 2:] -= crop_box[:2]
mask = np.logical_and(mask, (boxes[:, :2] < boxes[:, 2:]).all(axis=1))
boxes = boxes * np.expand_dims(mask.astype('float32'), axis=1)
labels = labels * mask.astype('float32')
boxes[:, 0], boxes[:, 2] = (boxes[:, 0] + boxes[:, 2]) / 2 / w, (
boxes[:, 2] - boxes[:, 0]) / w
boxes[:, 1], boxes[:, 3] = (boxes[:, 1] + boxes[:, 3]) / 2 / h, (
boxes[:, 3] - boxes[:, 1]) / h
return boxes, labels, mask.sum()
# 随机裁剪
def random_crop(img,
boxes,
labels,
scales=[0.3, 1.0],
max_ratio=2.0,
constraints=None,
max_trial=50):
if len(boxes) == 0:
return img, boxes
if not constraints:
constraints = [(0.1, 1.0), (0.3, 1.0), (0.5, 1.0), (0.7, 1.0),
(0.9, 1.0), (0.0, 1.0)]
img = Image.fromarray(img)
w, h = img.size
crops = [(0, 0, w, h)]
for min_iou, max_iou in constraints:
for _ in range(max_trial):
scale = random.uniform(scales[0], scales[1])
aspect_ratio = random.uniform(max(1 / max_ratio, scale * scale), \
min(max_ratio, 1 / scale / scale))
crop_h = int(h * scale / np.sqrt(aspect_ratio))
crop_w = int(w * scale * np.sqrt(aspect_ratio))
crop_x = random.randrange(w - crop_w)
crop_y = random.randrange(h - crop_h)
crop_box = np.array([[(crop_x + crop_w / 2.0) / w,
(crop_y + crop_h / 2.0) / h,
crop_w / float(w), crop_h / float(h)]])
iou = multi_box_iou_xywh(crop_box, boxes)
if min_iou <= iou.min() and max_iou >= iou.max():
crops.append((crop_x, crop_y, crop_w, crop_h))
break
while crops:
crop = crops.pop(np.random.randint(0, len(crops)))
crop_boxes, crop_labels, box_num = box_crop(boxes, labels, crop, (w, h))
if box_num < 1:
continue
img = img.crop((crop[0], crop[1], crop[0] + crop[2],
crop[1] + crop[3])).resize(img.size, Image.LANCZOS)
img = np.asarray(img)
return img, crop_boxes, crop_labels
img = np.asarray(img)
return img, boxes, labels
随机缩放
# 随机缩放
def random_interp(img, size, interp=None):
interp_method = [
cv2.INTER_NEAREST,
cv2.INTER_LINEAR,
cv2.INTER_AREA,
cv2.INTER_CUBIC,
cv2.INTER_LANCZOS4,
]
if not interp or interp not in interp_method:
interp = interp_method[random.randint(0, len(interp_method) - 1)]
h, w, _ = img.shape
im_scale_x = size / float(w)
im_scale_y = size / float(h)
img = cv2.resize(
img, None, None, fx=im_scale_x, fy=im_scale_y, interpolation=interp)
return img
随机翻转
# 随机翻转
def random_flip(img, gtboxes, thresh=0.5):
if random.random() > thresh:
img = img[:, ::-1, :]
gtboxes[:, 0] = 1.0 - gtboxes[:, 0]
return img, gtboxes
随机打乱真实框排列顺序
# 随机打乱真实框排列顺序
def shuffle_gtbox(gtbox, gtlabel):
gt = np.concatenate(
[gtbox, gtlabel[:, np.newaxis]], axis=1)
idx = np.arange(gt.shape[0])
np.random.shuffle(idx)
gt = gt[idx, :]
return gt[:, :4], gt[:, 4]
图像增广方法
# 图像增广方法汇总
def image_augment(img, gtboxes, gtlabels, size, means=None):
# 随机改变亮暗、对比度和颜色等
img = random_distort(img)
# 随机填充
img, gtboxes = random_expand(img, gtboxes, fill=means)
# 随机裁剪
img, gtboxes, gtlabels, = random_crop(img, gtboxes, gtlabels)
# 随机缩放
img = random_interp(img, size)
# 随机翻转
img, gtboxes = random_flip(img, gtboxes)
# 随机打乱真实框排列顺序
gtboxes, gtlabels = shuffle_gtbox(gtboxes, gtlabels)
return img.astype('float32'), gtboxes.astype('float32'), gtlabels.astype('int32')
这里得到的img数据数值需要调整，需要除以255，并且减去均值和方差，再将维度从[H, W, C]调整为[C, H, W]
img, gt_boxes, gt_labels, scales = get_img_data_from_file(record)
size = 512
img, gt_boxes, gt_labels = image_augment(img, gt_boxes, gt_labels, size)
mean = [0.485, 0.456, 0.406]
std = [0.229, 0.224, 0.225]
mean = np.array(mean).reshape((1, 1, -1))
std = np.array(std).reshape((1, 1, -1))
img = (img / 255.0 - mean) / std
img = img.astype('float32').transpose((2, 0, 1))
img
将上面的过程整理成一个函数get_img_data
def get_img_data(record, size=640):
img, gt_boxes, gt_labels, scales = get_img_data_from_file(record)
img, gt_boxes, gt_labels = image_augment(img, gt_boxes, gt_labels, size)
mean = [0.485, 0.456, 0.406]
std = [0.229, 0.224, 0.225]
mean = np.array(mean).reshape((1, 1, -1))
std = np.array(std).reshape((1, 1, -1))
img = (img / 255.0 - mean) / std
img = img.astype('float32').transpose((2, 0, 1))
return img, gt_boxes, gt_labels, scales
In [ ]
TRAINDIR = '/home/aistudio/work/insects/train'
TESTDIR = '/home/aistudio/work/insects/test'
VALIDDIR = '/home/aistudio/work/insects/val'
cname2cid = get_insect_names()
records = get_annotations(cname2cid, TRAINDIR)
record = records[0]
img, gt_boxes, gt_labels, scales = get_img_data(record, size=480)
批量数据读取与加速
上面的程序展示了如何读取一张图片的数据并加速，下面的代码实现了批量数据读取。
# 获取一个批次内样本随机缩放的尺寸
def get_img_size(mode):
if (mode == 'train') or (mode == 'valid'):
inds = np.array([0,1,2,3,4,5,6,7,8,9])
ii = np.random.choice(inds)
img_size = 320 + ii * 32
else:
img_size = 608
return img_size
# 将 list形式的batch数据 转化成多个array构成的tuple
def make_array(batch_data):
img_array = np.array([item[0] for item in batch_data], dtype = 'float32')
gt_box_array = np.array([item[1] for item in batch_data], dtype = 'float32')
gt_labels_array = np.array([item[2] for item in batch_data], dtype = 'int32')
img_scale = np.array([item[3] for item in batch_data], dtype='int32')
return img_array, gt_box_array, gt_labels_array, img_scale
# 批量读取数据，同一批次内图像的尺寸大小必须是一样的，
# 不同批次之间的大小是随机的，
# 由上面定义的get_img_size函数产生
def data_loader(datadir, batch_size= 10, mode='train'):
cname2cid = get_insect_names()
records = get_annotations(cname2cid, datadir)
def reader():
if mode == 'train':
np.random.shuffle(records)
batch_data = []
img_size = get_img_size(mode)
for record in records:
#print(record)
img, gt_bbox, gt_labels, im_shape = get_img_data(record,
size=img_size)
batch_data.append((img, gt_bbox, gt_labels, im_shape))
if len(batch_data) == batch_size:
yield make_array(batch_data)
batch_data = []
img_size = get_img_size(mode)
if len(batch_data) > 0:
yield make_array(batch_data)
return reader
由于数据预处理耗时较长，可能会成为网络训练速度的瓶颈，所以需要对预处理部分进行优化。通过使用飞桨提供的API paddle.reader.xmap_readers可以开启多线程读取数据，具体实现代码如下。
import functools
import paddle
# 使用paddle.reader.xmap_readers实现多线程读取数据
def multithread_loader(datadir, batch_size= 10, mode='train'):
cname2cid = get_insect_names()
records = get_annotations(cname2cid, datadir)
def reader():
if mode == 'train':
np.random.shuffle(records)
img_size = get_img_size(mode)
batch_data = []
for record in records:
batch_data.append((record, img_size))
if len(batch_data) == batch_size:
yield batch_data
batch_data = []
img_size = get_img_size(mode)
if len(batch_data) > 0:
yield batch_data
def get_data(samples):
batch_data = []
for sample in samples:
record = sample[0]
img_size = sample[1]
img, gt_bbox, gt_labels, im_shape = get_img_data(record, size=img_size)
batch_data.append((img, gt_bbox, gt_labels, im_shape))
return make_array(batch_data)
mapper = functools.partial(get_data, )
return paddle.reader.xmap_readers(mapper, reader, 8, 10)
至此，我们完成了如何查看数据集中的数据、提取数据标注信息、从文件读取图像和标注数据、图像增广、批量读取和加速等过程，通过multithread_loader可以返回img, gt_boxes, gt_labels, im_shape等数据，接下来就可以将它们输入到神经网络，应用到具体算法上了。
在开始具体的算法讲解之前，先补充一下读取测试数据的代码。测试数据没有标注信息，也不需要做图像增广，代码如下所示。
# 测试数据读取
# 将 list形式的batch数据 转化成多个array构成的tuple
def make_test_array(batch_data):
img_name_array = np.array([item[0] for item in batch_data])
img_data_array = np.array([item[1] for item in batch_data], dtype = 'float32')
img_scale_array = np.array([item[2] for item in batch_data], dtype='int32')
return img_name_array, img_data_array, img_scale_array
# 测试数据读取
def test_data_loader(datadir, batch_size= 10, test_image_size=608, mode='test'):
"""
加载测试用的图片，测试数据没有groundtruth标签
"""
image_names = os.listdir(datadir)
def reader():
batch_data = []
img_size = test_image_size
for image_name in image_names:
file_path = os.path.join(datadir, image_name)
img = cv2.imread(file_path)
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
H = img.shape[0]
W = img.shape[1]
img = cv2.resize(img, (img_size, img_size))
mean = [0.485, 0.456, 0.406]
std = [0.229, 0.224, 0.225]
mean = np.array(mean).reshape((1, 1, -1))
std = np.array(std).reshape((1, 1, -1))
out_img = (img / 255.0 - mean) / std
out_img = out_img.astype('float32').transpose((2, 0, 1))
img = out_img #np.transpose(out_img, (2,0,1))
im_shape = [H, W]
batch_data.append((image_name.split('.')[0], img, im_shape))
if len(batch_data) == batch_size:
yield make_test_array(batch_data)
batch_data = []
if len(batch_data) > 0:
yield make_test_array(batch_data)
return reader
单阶段目标检测模型YOLO-V3
本次课程主要向我们介绍了YOLO-V3的应用。
YOLO-V3 模型设计思想
YOLO-V3算法的基本思想可以分成两部分：
按一定规则在图片上产生一系列的候选区域，然后根据这些候选区域与图片上物体真实框之间的位置关系对候选区域进行标注。跟真实框足够接近的那些候选区域会被标注为正样本，同时将真实框的位置作为正样本的位置目标。偏离真实框较大的那些候选区域则会被标注为负样本，负样本不需要预测位置或者类别。
使用卷积神经网络提取图片特征并对候选区域的位置和类别进行预测。这样每个预测框就可以看成是一个样本，根据真实框相对它的位置和类别进行了标注而获得标签值，通过网络模型预测其位置和类别，将网络预测值和标签值进行比较，就可以建立起损失函数。
产生候选区域
如何产生候选区域，是检测模型的核心设计方案。目前大多数基于卷积神经网络的模型所采用的方式大体如下：
按一定的规则在图片上生成一系列位置固定的锚框，将这些锚框看作是可能的候选区域，
对锚框是否包含目标物体进行预测，如果包含目标物体，还需要预测所包含物体的类别，以及预测框相对于锚框位置需要调整的幅度。
生成锚框
生成锚框的主要主要操作就是将图片分割成m×n个小方块，然后以每一个小方块的中心为中心点，画出若干个同心矩形框。矩形框的具体大小由数据库中所有真实框聚类决定。
生成预测框
在前面已经指出，锚框的位置都是固定好的，不可能刚好跟物体边界框重合，需要在锚框的基础上进行位置的微调以生成预测框。而微调的参数则是我们需要训练的参数。
标注候选区域
每个区域可以产生3种不同形状的锚框，每个锚框都是一个可能的候选区域，对这些候选区域我们希望知道这么几件事情：
-
锚框是否包含了物体，这可以看成是一个二分类问题，包含了物体和没有包含物体，我们使用标签objectness来表示。当锚框包含了物体时，objectness=1，表示预测框属于正类；当锚框不包含物体时，设置objectness=0，表示锚框属于负类。
-
如果锚框包含了物体，那么它对应的预测框的中心位置和大小应该是多少，或者说上面计算式中的tx,ty,tw,th应该是多少。
-
如果锚框包含了物体，那么具体类别是什么，这里使用变量label来表示其所属类别的标签。
卷积神经网络提取特征
在检测问题中，也使用卷积神经网络逐层提取图像特征，通过最终的输出特征图来表征物体位置和类别等信息。
YOLO-V3算法使用的骨干网络是Darknet53。Darknet53网络的具体结构如图所示。
建立损失函数
对于每个预测框，YOLO-V3模型会建立三种类型的损失函数：
-
表征是否包含目标物体的损失函数，通过pred_objectness和label_objectness计算
-
表征物体位置的损失函数，通过pred_location和label_location计算
-
表征物体类别的损失函数，通过pred_classification和label_classification计算
多层级检测
目前我们计算损失函数是在特征图P0的基础上进行的，它的步幅stride=32。特征图的尺寸比较小，像素点数目比较少，每个像素点的感受野很大，具有非常丰富的高层级语义信息，可能比较容易检测到较大的目标。为了能够检测到尺寸较小的那些目标，需要在尺寸较大的特征图上面建立预测输出。如果我们在C2或者C1这种层级的特征图上直接产生预测输出，可能面临新的问题，它们没有经过充分的特征提取，像素点包含的语义信息不够丰富，有可能难以提取到有效的特征模式。在目标检测中，解决这一问题的方式是，将高层级的特征图尺寸放大之后跟低层级的特征图进行融合，得到的新特征图既能包含丰富的语义信息，又具有较多的像素点，能够描述更加精细的结构。
开启端到端训练
训练过程的流程如下图所示，输入图片经过特征提取得到三个层级的输出特征图P0(stride=32)、P1(stride=16)和P2(stride=8)，相应的分别使用不同大小的小方块区域去生成对应的锚框和预测框，并对这些锚框进行标注。
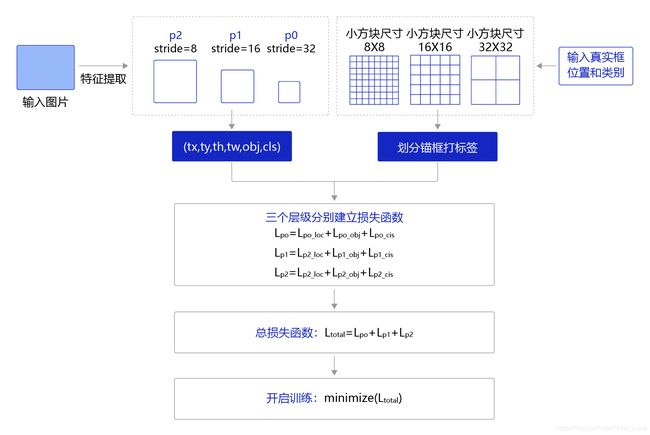
预测
预测过程流程图如下所示：
预测过程可以分为两步：
- 通过网络输出计算出预测框位置和所属类别的得分。
- 使用非极大值抑制来消除重叠较大的预测框。
非极大值抑制
我们使用非极大值抑制（non-maximum suppression, nms）来消除冗余框，其基本思想是，如果有多个预测框都对应同一个物体，则只选出得分最高的那个预测框，剩下的预测框被丢弃掉。那么如何判断两个预测框对应的是同一个物体呢，标准该怎么设置？如果两个预测框的类别一样，而且他们的位置重合度比较大，则可以认为他们是在预测同一个目标。非极大值抑制的做法是，选出某个类别得分最高的预测框，然后看哪些预测框跟它的IoU大于阈值，就把这些预测框给丢弃掉。
写在最后的话
感谢飞桨Paddle提供的这次机会，可以很好的学习到深度学习的相关知识。