理解Word2Vec模型

参考资料：
https://www.bilibili.com/video/BV1pt411h7aT?p=2
https://zhuanlan.zhihu.com/p/27234078utm_source=qq&utm_medium=social&utm_oi=1015991733942931456

首言

你好，我是Wumbuk。最近有看有关于NLP相关知识，所以利用CSDN简单记录一下Word2Vec方法。Word2Vec方法是用来产生词向量相关模型的一种方法，在进行自然语言处理的时候，我们不可能将词语以本来的形式输入到神经网络的系统中，而是将每一个词都用多维向量表示，同时呢保证该向量的表示方法可以明确地表示出各种不同词之间的关系和预测。
Word2Vec方法通过学习文本来用词向量的方式来表征词的语义信息，通过一个嵌入空间表示不同语义的单词。两个词之间的语义愈相近，它们之间的欧式距离就越短。

下面是百度百科的解释：

Word2vec，是一群用来产生词向量的相关模型。这些模型为浅而双层的神经网络，用来训练以重新建构语言学之词文本。网络以词表现，并且需猜测相邻位置的输入词，在word2vec中词袋模型假设下，词的顺序是不重要的。训练完成之后，word2vec模型可用来映射每个词到一个向量，可用来表示词对词之间的关系，该向量为神经网络之隐藏层。

在Word2Vec 模型中，包括两种： Skip-Gram和CBOW。前者的作用是给定中心词来预测上下文（窗口）中其余各种词出现的概率，取概率最大的词作为预测值。而CBOW恰好相反，其作用是给定上下文（周围词）来榆次input word（中心词）。本篇文章重点围绕SkipGram模型展开。

一、SG模型中的名词解释

SG模型(Skip-Gram)的作用就是给定一个中心词($W_t$)，该中心词经过神经网络后预测其周围词的内容（$W_{t-1},W_{t+1},W_{t-2}，W_{t-2},W_{t-3}，W_{t+3}，...$）,如下图所示。

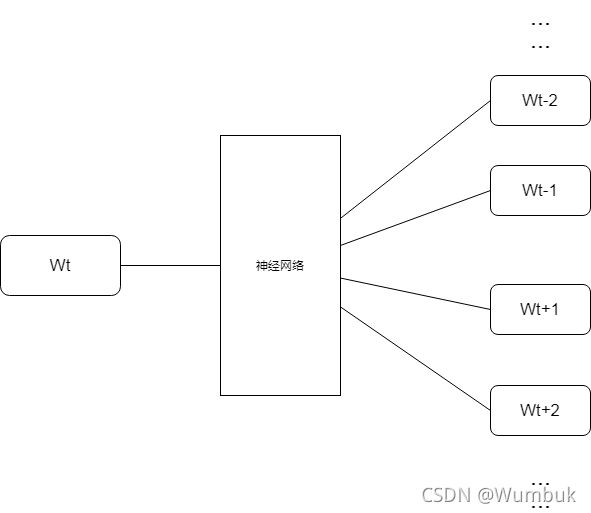
为了完成上述的功能，Word2Vec模型实际上是分成了两个部分，第一个部分就是要建立模型，第二个部分就是获得嵌入词向量。Word2Vec的整个建模过程简单地说就是先基于训练数据构建一个神经网络，当这个模型训练好之后，我们并不是立即用这个训练好的模型去进行处理任务，而是利用到其中的训练好的参数。也就是说，建模并不重要，而获取其中的参数最重要。

1.1. 独热码

 一种表示词向量的想法是利用独热码。独热码直观来说就是有多少个状态就有多少比特，而且只有一个比特为1，其他全为0的一种码制。显而易见地是这种码制可以表示出某一个单词，但是没有办法表示不同单词之间的关系。

 基于此，因为句子中不同的单词之间具有某种关系，我们的目标就是通过大量的训练集给每一个词构造一个响亮，选择一个密集型的向量，让它可以预测目标单词所在文本的其他词汇。

1.2 建模过程

我们在上面提到过，训练模型的真正目的是获取模型基于训练集所得到的最优参数$\Theta$（$\Theta$以后讨论）。为了得到这些权重，我们首先需要构造一个完整的神经网络作为模型，然后再用这个网络通过反向传播等方法间接地获取我们的词向量。
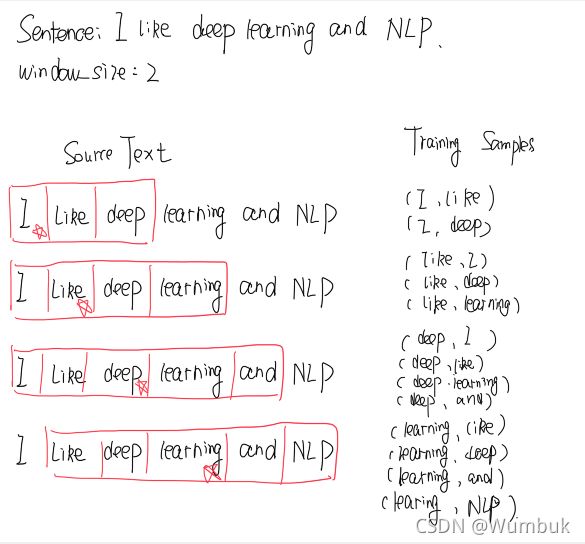
接下来，我们具体看看我们模型的作用机理。假如我现在有一个句子 “I like deep learning and NLP”

1. 首先我们选择句子中的一个词作为我们的中心词，即key word。就是说，我们输入这个词，看看其周围的词是什么？ 我们选取learning 作为input word.
2. 有了input word之后，我们还需要定义一个skip_window的超参数，它代表当前窗口一侧的大小(不包括中心词).比如，如果我们设置skip_window=2，那么我们窗口中的内容（包括input word）为
   {‘I’,‘like’,‘deep’,‘learning’,‘and’} 。另外一个超参数叫num_skips，它代表着我们从整个窗口中选取多少个不同的词作为我们的output word,例如，如果num_skips=2，则我们将得到两组 (input word,output word) 形式的训练数据，即 (‘deep’,‘like’),(‘deep’,‘learning’)
3. 训练好的神经网络将会基于我们的输入给出一个矩阵形式的概率分布，分别表示的是某一个词作为特定位置的预测的可能性。这个具体的向量表示，将会在后面进行展示。

  模型的输出的某个对应概率就代表着词典中某个词有多大概率和input word同时出现。举个例子，如果我们向神经网络模型中输入一个单词" Cat “，那么在最终的预测结果中，像"Tiger”,“Fish"这种词汇就要比"cup”,“melon"这种词出现的概率高。因为"Tiger”,"Fish"作为训练集的文本中更大可能在"cat"的窗口中出现。
下图以“I like deep learing and NLP”为例子，进行训练过程的一个简单演示：

二、SG模型的损失函数

我们用$P(context|W_t)$表示以$W_t$预测周围context内容的准确性。

2.1表达形式1

$$J^1=\prod _{t=1}^T\prod _{-m\le j\le m,j\ne 0}P(W_{t+j}|W_t;\theta )(2-1)$$
如上所示，式2-1可以作为衡量损失函数的一种方式，其中T表示我们当前所经过的时间步，即经过了T个中心词。j表示以中心词为中心，预测周围的第j个单词。$\theta$表示神经网络中所有的参数。由P的意义不难得出，我们的目的是让$J^1$的值最小。

2.2 表达形式2

$$J=-\frac{1}{T}\sum _{t=1}^T\sum _{-m\le j\le m,j\ne 0}logP(W_{t+j}|W_t)(2-2)$$
我们借鉴于 极大似然估计的思想，通过取对数操作，将原来的乘法操作改变成对数的加法操作。又因为我们在式3-2的前面加了一个负号，所以预测效果最好就等价于 取J的最小值。

2.3 softmax函数

  softmax函数的表达式为 $\frac{e^x}{\sum e^x}$，该函数可以将数据归一化，并且所有情况之和为1.对于值越大的数据，其压缩后的所占的概率就越大；对于值越小的数据，其压缩后所占的概率就越小。

---

基于上面的介绍，我们引进矩阵u和矩阵v：
其实在神经网络中，正如在前面提到过的，我们将所有的未知参数都设为$\theta$，我们的目标就是找出最优的$\theta$，假设我们的词典包含的是从a~z开头的单词集，即{adventure,a…,…,zebra,zoo}，则有
$$\theta =\left[\begin{array}{c}{v}_{adventure}\\ v_{a..}\\ v_{...}\\ v_{zebra}\\ v_{zoo}\\ u_{adventure}\\ u_{a..}\\ u_{...}\\ u_{zebra}\\ u_{zoo}\end{array}\right]\theta \in R^{2dv}(式2-3)$$
值得注意的是，$\theta$的定义告诉我们每个单词有两个向量。其中v向量表示的是中心词向量，u向量表示的是周围词向量。这两个向量是我们最后需要求出来的参数。
定义：
若有v个单词，并且每个单词都由d维向量进行表示
$$P(O|C)=\frac{exp(u_o^T{v}_c)}{{\sum }_{w=1}^{v}exp(u_w^T{v}_c)}(式2-4)$$
其中，P(O|C)表示以单词C为中心，单词O为临近词这种情况发生的归一化后的概率。且有$u^{T}v={\sum }_{i=1}^d{u}_i{v}_i$。

三、模型的计算过程

3.1 数据的表示

 首先，我们知道。神经网络只能接受数值的输入，我们不可能将一个完成的单词输入到网络中。最常用的办法就是基于训练文档来构建我们自己的词汇表，然后再对词汇表进行ont-hot编码。
比如还是上面的例子，对于句子"I like deep learning and NLP",我们基于这个句子，可以构建一个大小为6的词汇表 {‘I’,‘like’,‘deep’,‘learning’,‘and’}.那么单词’deep’就可以表示为向量 : **$deep=[0,0,1,0,0,0{]}^T$**的6维向量。
 如果模型输入的是6维的向量，那么输出也是一个6维的向量(6刚好是我们词典的大小)，并且它会在每一个维度上都包含一个概率，每一个概率表示的是当前词是输入样本中output word的概率大小。

3.2 隐层

说完单词的编码和训练样本的选取，我们来看一下隐层(前面提到的$\theta$参数)。假设我们使用300个特征去表示一个单词(每个单词可以用一个300维的向量进行表示)。那么该隐层的权重矩阵就是$300\times 6$

我们的目标之一就是求出最终的这个矩阵。
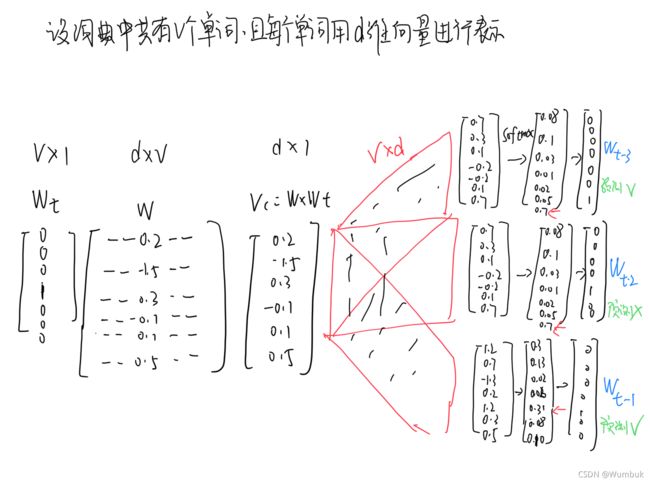
我们将问题泛化，假设我们的每个单词用d维向量进行表示，词典中共有v个单词。记上面的权重矩阵为w。有独热码$w_t$表示矩阵为$v\times 1$维，w矩阵为$d\times v$维矩阵。
所以$w_t\times w$两个矩阵相乘，隐层神经网络输出的是一个$d\times 1$维矩阵，将此结果记为$v_c$。

3.3 输出层

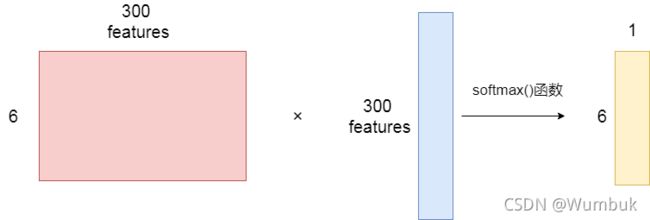
经过神经网络层的计算，输入的input word会从变成$v_c$,然后再被输入到输出层。输出层是一个softmax回归分类器，它的每一个节点都会输出一个0-1之间的概率，并且保证通过softmax函数实现的所有输出层神经元结点的概率之和为1。
下图为示例步骤

3.4 SG模型的计算过程

由2.3节得$P(O|C)=\frac{exp(u_o^T{v}_c)}{{\sum }_{w=1}^{v}exp(u_w^T{v}_c)}$，其所对应SG模型计算过程如下：

3.5 SG模型参数$\theta$确定的数学证明

这里只以$\theta$中的中心向量$v_c$求偏导为例
由3.1-3.4 的讲解，我们有目标函数(式2-4)$$P(O|C)=\frac{exp(u_o^T{v}_c)}{{\sum }_{w=1}^{v}exp(u_w^T{v}_c)}$$

对于变量$v_c$，该函数的最小值点的导数为0.我们有
$$\frac{\partial log\frac{exp(u_0^T{v}_c)}{{\sum }_{w=1}^{v}exp(u_w^T{v}_c)}}{\partial v_c}=\frac{\partial [logexp(u_0^T{v}_c)-{\sum }_{w=1}^{v}exp(u_w^T{v}_c)]}{\partial v_c}$$
我们分别标记前半部分为①，后半部分为②。
对①：
$$原式=\frac{\partial u_0^T{v}_c}{\partial v_c}=u_0$$
对②：

所以，为了让损失函数最小，我们令 导数为0，即①-②=0，得到
$$u_o-\sum _{x=1}^{v}p(x|c)u_x$$
其中$u_o$表示的是实际上观测的值，后面的一项则是u的期望。也就是说，为了让预测的效果最好，我们就要调节参数$v_c$，令导数的结果为0。 同理，在处理其他的参数的时候，我们采取类似的做法。

四、高级词向量表示

4.1常规训练导致的问题

在神经网络中，我们对参数优化的方法为 随机梯度下降法SGD(不具体展开啦，感兴趣的小伙伴可以看看这个 梯度下降法)。由式2-3得待优化的参数为$\theta$，结合梯度下降法得：
$${\theta }_j^{new}={\theta }_j^{old}-\alpha \frac{\partial J(\theta )}{\partial {\theta }_j}(式4-1)$$
随机梯度下降法本身就是为了克服数据量过大，我们随机的选取数据进行梯度的更新。
$${\theta }_j^{new}={\theta }_j^{old}-\alpha {▽}_{\theta }{J}_t(\theta )(式4-2)$$
但是，即使如此。我们仍然面临着数据量过大的问题。比如我们有一个10000个单词的词汇表，每一个单词用300维的向量表示，那么我们的两种权重矩阵v和u都会有10000*300=300万个权重，在如此庞大的神经网络中进行梯度下降时间复杂度是相当不合适的。
所以提出了以下的几种解决方案：

1. 负采样

4.2 负采样 negative sampling

 我们以式 2-4作为 梯度下降方法中的目标函数。则由其定义内容，假设文本句子的长度为v(词汇表中有v个单词)，对某一个位置的中心词，分子部分都需要进行1次矩阵的乘法运算，而分母部分需要v次矩阵乘法运算。共有v个中心词，由因为1次矩阵相乘的复杂度O(d*1)，所以总的时间复杂度为$(v^{2}d)$,这是一个很高的时间复杂度，我们要想办法克服。
 仔细观察，可以发现,其实u,v矩阵是两个很蓬松的的矩阵。对于语义相同的上下文词汇其矩阵相乘会有意义；而对于大多数不太相关词来说，其矩阵相乘的值趋近与零，对于这种情况，我们完全不用去计算。
设目标函数为：
$$\begin{gathered} J(\theta )=\frac{1}{T}\sum _{t=1}^T{J}_t(\theta )(式4-3) \\ {J}_t(\theta )=log\sigma (u_o^t{v}_c)+\sum _{i=1}^k{E}_{j\sim p(w)}[log\sigma (-u_j^T{v}_c)]（式4-4） \end{gathered}$$
其中$\sigma$表示的是sigmoid函数。式4-4从某种角度可以看成是由式2-4通过取对数得到，我们要保证这个目标函数取得最大值就等价于：第一项表示要最大化真实出现的外围词的概率，第二项表示最小化中心词周围出现的随机词的概率。
 简单地再理解一下：式4-3和式4-4就表示T时刻时我们观察到的在中心词周围出现的词向量实际是周围词o(就是$u_o$的下标),然后就根据实际情况最大化目标函数。如何最大化目标函数呢？通过调整$\theta$；如何调整$\theta$呢？通过梯度下降法。
 在式4-4中,我们称后面一项为负采样(negative words),也就是说为了加快训练的速度，我们不再是对每个词向量都进行计算，而是选取几个代表的词来进行计算，这样做的好处是减少了无用的计算，加快了模型收敛速度；另以方面实际上证明这样做也会有更好的效果。
代码中P：
$$P(w^i)=\frac{f(w_i{)}^{\frac{3}{4}}}{{\sum }_{j=0}^n(f(w_j{)}^{\frac{3}{4}})}$$
我们给每一个单词被赋予一个权重，即$f(w_i)$，它代表单词出现的频次。公式中的3/4是一个完全基于经验得到的参数。

总结