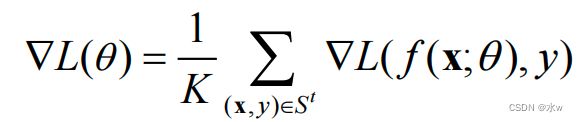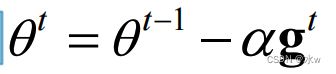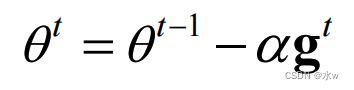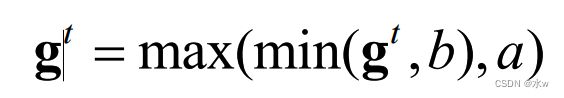深度学习之 8 深度模型优化与正则化

本文是接着上一篇深度学习之 7 深度前馈网络2_水w的博客-CSDN博客

目录

深度模型优化与正则化

1.网络优化

（1）非凸优化问题

（2）网络优化的改善方法

 2.小批量梯度下降

（1）批量梯度下降(batch gradient descent)

（2）随机梯度下降(stochastic gradient descent)

（3）小批量梯度下降(minibatch gradient descent) 

 （4）随机梯度下降 vs 批量梯度下降 vs 小批量梯度下降

（5）批量大小(batch-size) K 的影响

 3.学习率与梯度优化

（1）学习率衰减

（2）学习率预热

（3）周期性学习率调整​​​​​​​

（4）从学习率衰减到自适应学习率

（5）梯度修正

        1） 动量法：为了逃出极值点

        2）Adam算法：自适应学习率（RMSprop）+梯度方向优化（动量法）

        3）各优化算法比较

（6）梯度截断：为了防止梯度爆炸

（7）总结：

---

深度模型优化与正则化

1.网络优化

优化问题：

◼ 神经网络模型是一个非凸函数，再加上在深度网络中的梯度消失问题，很难进行优化；

◼ 深层神经网络模型一般参数比较多，训练数据也比较大，会导致训练的效率比较低。

◼ 网络优化的难点：

        ➢ 网络结构多样性：

                ✓ 神经网络种类繁多：FNN、CNN、RNN、GNN

                ✓ 不用网络结构不同，不同参数的作用有差异

                ✓ 很难找到一种通用的、高效的、稳定的优化方法

                ✓ 超参数一般也比较多

        ➢ 非凸优化问题：

                ✓ 如何初始化参数

                ✓ 如何逃离局部最优        

                ✓ 深度神经网络的参数非常多，其优化是高维空间中的非凸优化问题

（1）非凸优化问题

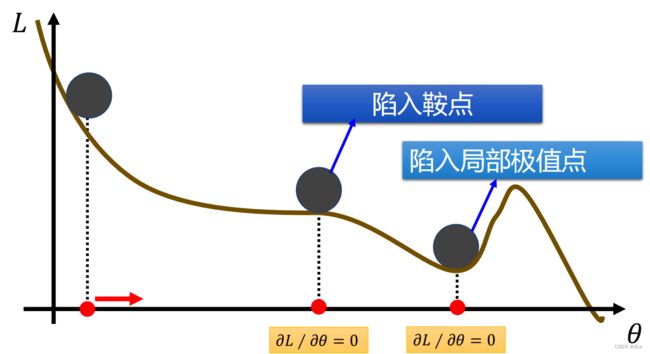
⚫ 在高维空间中，非凸优化最大难点并不在于如何逃离局部最优点，而是如何逃离鞍点。 

⚫ 一阶导数：

⚫ 二阶导数：

        当，成为驻点

        如果的所有特征值为正，为局部最小点

        如果的所有特征值为负，为局部最大点

        如果的特征值有正有负，为鞍点

 ⚫ 在高维空间中，局部最小值（Local Minima）要求在每一维度上都是最低点，这种概率非常低。也就说是，高维空间中大部分驻点都是鞍点。

（2）网络优化的改善方法

改善网络优化的方法的目标是找到更好的局部最小值和提高优化效率。

 2.小批量梯度下降

（1）批量梯度下降(batch gradient descent)

每次更新都使用整个训练集数据；需要较多计算资源（有一万个样本，我就需要计算一万次）；

（2）随机梯度下降(stochastic gradient descent)

每次只挑选一个样本，只用一个样本来计算梯度。 

（3）小批量梯度下降(minibatch gradient descent) 

几个关键因素：

        ➢ 小批量样本数量：K 

        ➢ 梯度：gt 

        ➢ 学习率：α 

➢ 选取包含个样本的小批量（MiniBatch）样本集，计算偏导数：

➢ 定义梯度：

➢ 更新参数：

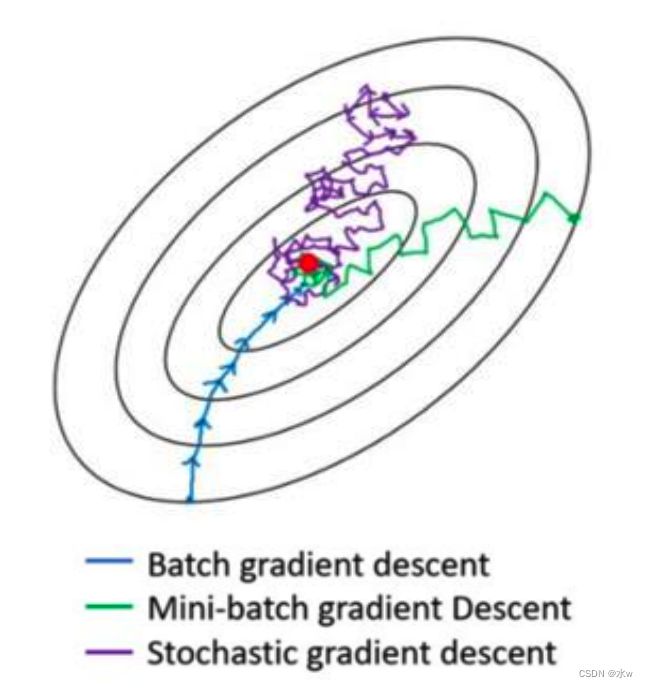
 （4）随机梯度下降 vs 批量梯度下降 vs 小批量梯度下降

➢ 批量梯度下降：利于寻找全局最优解，梯度方差小；但样本数目很多时，训

练过程会很慢。

➢ 随机梯度下降：训练速度快；准确度下降，不利于寻找全局最优，梯度方

差大。

➢ 小批量梯度下降法：同时兼顾两种方法的优点。

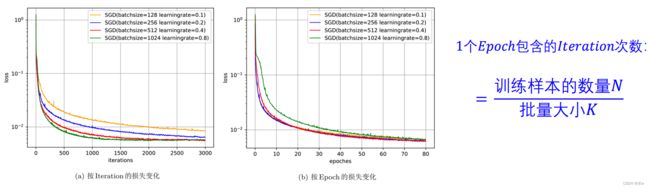
（5）批量大小(batch-size) K 的影响

批量大小不影响梯度的期望，但是会影响梯度的方差。 

        ➢ 批量越大，梯度的方差越小，训练也越稳定，因此可以设置较大的学习率。

        ➢ 批量较小时，需要设置较小的学习率，否则模型会不收敛。

 3.学习率与梯度优化

学习率的影响：

        • 学习率过大：不收敛

        • 学习率过小：收敛太慢

（1）学习率衰减

根据经验，学习率在一开始要保持大些来保证收敛速度，收敛到最优点附近时要小些以避免来回震荡。

         ➢ 开始时，距离极值点处很远，采用大些的学习率，尽快接近极值点。 

        ➢ 迭代多次后，接近极值点处，减小学习率，保证收敛，避免震荡。 

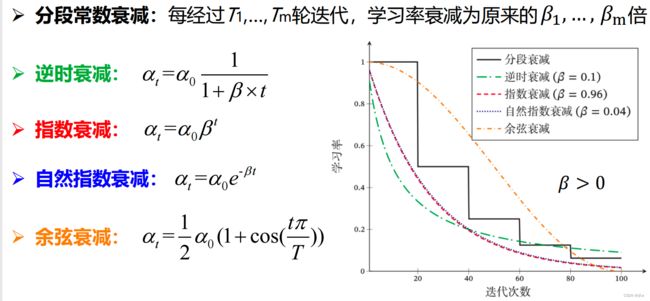
        ➢ 多种减小学习率的方式

分类： 

 这几种方法都是单调递减的，肯定学习率会越来越小的，那么这种学习率一开始最大，后来越来越小的方法一定是很合适的吗？它也存在着问题。

（2）学习率预热

当batch-size比较大时，需要比较大的学习率。但开始训练的参数是随机初始化的，梯度往往也比较大，加上比较大的初始学习率，会使得训练不稳定。

        ➢ 学习率预热：为提高训练稳定性，可以在最初几轮迭代时采用较小的学习率，等梯度下降到一定程度后再恢复到初始学习率；

        ➢ 逐渐预热（Gradual Warmup）：假设预热的迭代次数为 ，预热过程中，学习率为

        ➢ 当预热过程结束，再选择一种学习率衰减方法来逐渐降低学习率。

这种预热是一个先上升，再下降的过程。那么有时候我们为了逃离局部最小值或者鞍点，我们周期性地增大学习率，不能让它到顶点就单调下降，单调下降到一定程度之后又突然增加，学习率突然增加意味着参数变化突然加快，突然加快就意味着可以跳出局部极值点。 

（3）周期性学习率调整

为了逃离局部最小值或鞍点，可在训练过程中周期性地增大学习率。短期内有损收敛稳定性，长期来看有助于找到更好的局部最优解。

        ➢ 循环学习率：让学习率在一个区间内周期性地增大和缩小。

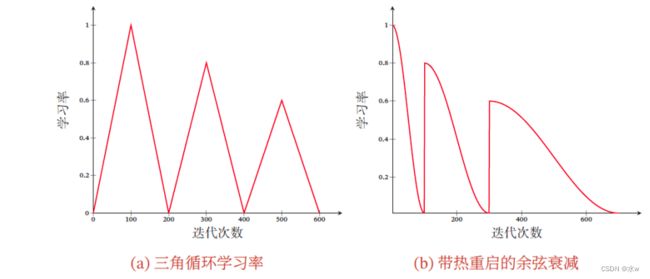
                ⚫ 三角循环学习率(Triangular Cyclic Learning Rate)：使用线性缩放来调整学习率

                ⚫ 带热重启的随机梯度下降：周期性地重启并采用余弦衰减

 好处：周期性学习率调整，有助于逃离局部极值点（走错了也没关系，最终还是有很大概率找到最优点的）。

 （4）从学习率衰减到自适应学习率

学习率衰减的局限性：

        ➢ 非自适应，不能够根据当前梯度情况做出调整；

        ➢ 每个参数的收敛速度各不相同，应该根据不同参数的收敛情况分别设置学习率。

从稀疏特征的角度来看：

        ➢ 某些特征出现的频率较低，与其相关的参数更新的频率也比较低；

        ➢ 常见特征的相关参数可以迅速地收敛到最佳值；

        ➢ 而不常见特征的相关参数由于缺乏足够的观测样本，所以其最佳值难以确定；

        ➢ 学习率要么对于常见特征的相关参言衰减太慢，要么对于不常见特征的相关参数衰减太快。

◼ AdaGrad算法：Adaptive Gradient Algorithm

1）该算法借鉴了L2正则化的思想，每次迭代时，自适应地调整每个参数的学习率。

2）局限：在经过一定次数的迭代依然没有找到最优点时，由于这时的学习率已经非常小，很难再继续找到最优点。

◼ RMSprop算法

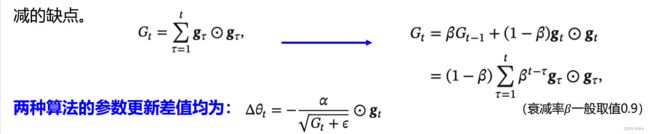
1）将Gt的计算由“梯度的平方的累积”方式变成了“梯度平方的指数衰减移动平均”, 可以在有些情况下避免AdaGrad算法中学习率不断单调下降以至于过早衰减的缺点。

AdaGrad的学习率不断衰减，而RMSProp学习率可能变大也可能变小 （取决于梯度累积的快慢）。

2）具体展开： 

 （5）梯度修正

1）如何逃离局部极值点或鞍点？

        ⚫ 在小批量梯度下降中，如果每次选取样本数量比较小，损失会呈现震荡的方式下降；

        ⚫ 随机梯度下降方法中每次迭代的梯度估计和整个训练集上的最优梯度并不一致，具有一定的随机性；

 2）那么如何缓解梯度的随机性？

        ⚫ 增加批量大小

        ⚫ 进行梯度修正

1） 动量法：为了逃出极值点

⚫ 动量（Momentum）是模拟物理中的概念．一个物体的动量指的是该物体在它运动方向上保持运动的趋势，是该物体的质量和速度的乘积。

⚫ 用之前积累动量来替代真正的梯度。每次迭代的梯度可看作加速度。 

⚫ 第t 次迭代，计算负梯度的“加权移动平均”作为参数的更新方向：

◼

 ⚫ 在迭代初期，梯度方向都比较一致，动量法会起到加速作用，可以更快地到达最优点。 

⚫ 在迭代后期，梯度方向会不一致，在收敛值附近震荡，动量法会起到减速作用，增加稳定性。

2）Adam算法：自适应学习率（RMSprop）+梯度方向优化（动量法）

3）各优化算法比较

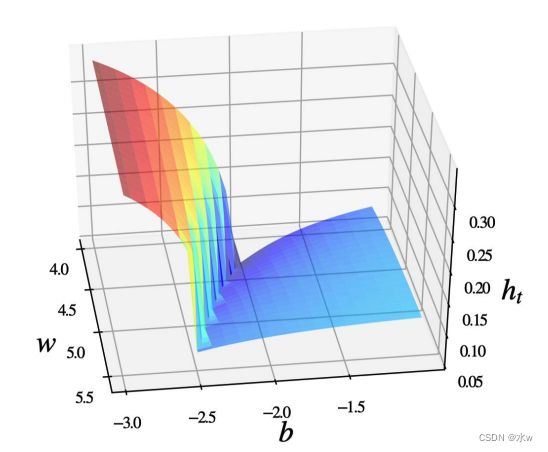
（6）梯度截断：为了防止梯度爆炸

⚫ 除了梯度消失之外，梯度爆炸也是影响学习效率的主要因素。

⚫ 为了避免这种情况，当梯度的模大于一定阈值时，就对梯度进行截断，称为梯度截断

⚫ 梯度截断是一种比较简单的启发式方法，把梯度的模限制在一个区间内；

        ➢ 按值截断

        ➢ 按模截断

（7）总结：