排序算法——快速排序(递归和非递归)及其优化(三数取中法、随机数法)
文章目录
- 快速排序
-
- 1.快速排序——使用递归
-
- 1.1快速排序基本思想
- 1.2快速排序的基本步骤
- 1.3性能分析
- 1.4源代码
- 2.快速排序的优化
-
- 2.1调用其他排序
- 2.2三数取中法
- 2.3随机数法
- 3.快速排序——不使用递归
-
- 3.1基本思想
- 3.2非递归快排源代码
- 3.3 性能分析
- 4.总结
快速排序
1.快速排序——使用递归
1.1快速排序基本思想
- 快速排序:通过一趟排序将待排序列分割成两个部分,其中一部分的所有值都小于基准值,另外一部分的值都大于基准值,然后再分别对这两部分进行快速排序,直到所有的值都全部有序(当子序列只有一个值的时候,不用对其再进行划分,默认其有序)即函数调函数,使用了递归的思想。
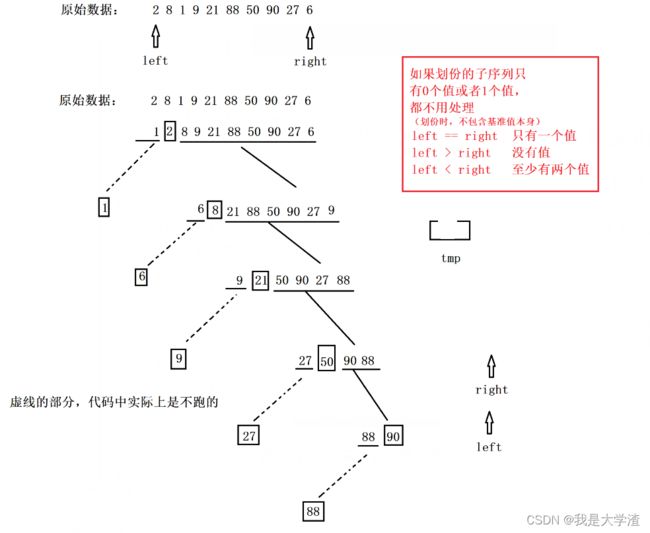
1.2快速排序的基本步骤
- 首先我们要进行第一次分割,第一次分割时的左右两指针就是数组的首尾两个指针(因为在最初我们只知道数组的长度,这个变量不能确定左右两个指针的范围,所以我们将长度转变为left和right两个指针来解决我们的问题)
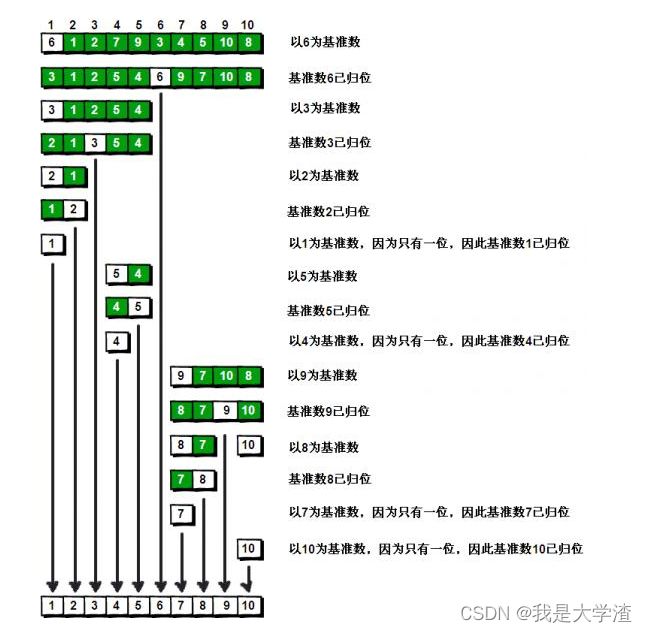
void Quick_Sort(int *arr, int len)
{
Quick(arr, 0, len-1);
}
- Quick函数就是我们需要用到的递归函数,par是这一趟分割函数中基准值最终所在的下标 ,如果左右两个序列中元素个数不唯一(用left < par-1 和par+1 < right 来控制),就继续调用该函数
void Quick(int *arr, int left, int right)
{
int par = Partition(arr, left, right);//par是这一趟分割函数中基准值最终所在的下标
//处理基准值左半部分
if(left < par-1)//保证基准值左半部分 至少有两个值
{
Quick(arr, left, par-1);//这时,左半部分有必要进行再次划份
}
//处理基准值右半部分
if(par+1 < right)//保证基准值右半部分 至少有两个值
{
Quick(arr, par+1, right);//这时,右半部分有必要进行再次划份
}
}
- 我们将每一个需要的功能用函数封装起来,核心函数就是——分割函数(Partition)函数,也是面试官爱问的函数之一。该函数先将left指向的值给temp,然后从右向左找一个比temp小的值,找到后就将其赋给left指向的值,没找到后就跳出循环,然后从左向右找到一个比temp大的值,找到后与right指向的值交换,循环往复直到左右两个指针相遇。
//快速排序的分割函数,划份函数 时间复杂度O(n) 空间复杂度O(1)
int Partition(int *arr, int left, int right)
{
//1.将第一个值看做基准值,用tmp保存
int tmp = arr[left];
while(left < right)//只要left和right两个指针没有相遇,则继续往复循环
{
while(left<right && arr[right] > tmp)//如果两个指针还未相遇,且right指向的值大于tmp,则right--
{
right--;
}
//此时while循环结束,只有两个可能:1.两个指针相遇 2.找到了小于tmp的值,由right指向
if(left == right)
{
/*arr[left] = tmp; //arr[right] = tmp; //left == right
return left; //return right;*/
break;
}
arr[left] = arr[right];
while(left<right && arr[left] <= tmp)//如果两个指针还未相遇,且left指向的值小于等于于tmp,则left++
{
left++;
}
//此时while循环结束,只有两个可能:1.两个指针相遇 2.找到了大于tmp的值,由left指向
if(left == right)
{
arr[left] = tmp; //arr[right] = tmp; //left == right
return left; //return right;
//break;
}
arr[right] = arr[left];
}
//此时,代码指向到这一行,代表着最大的while结束了,也就是说两个指针相遇了
//将tmp的值,重新放回来,然后返回基准值的下标
arr[left] = tmp; //arr[right] = tmp; //left == right
return left; //return right;
}
1.3性能分析
- 时间复杂度:最差O(n^2) 最优O(nlogn) 平均O(nlogn)
- 空间复杂度:因为快排递归的时候,申请的辅助空间未释放,所以不是O(1),是O(logn)
- 稳定性:不稳定
- 特点:数据越乱排序越快

1.4源代码
int Partition(int* arr, int left, int right)
{
int temp = arr[left];
while(left < right)
{
while (left<right && arr[right]>temp)
{
right--;
}
if (left == right)
{
break;
}
arr[left] = arr[right];
while (left<right && arr[left]<=temp)
{
left++;
}
if (left == right)
{
break;
}
arr[right] =arr[left];
}
arr[left] = temp;
return left;
}
void Quick(int* arr, int left, int right)
{
int par = Partition(arr, left, right);
if (left < par - 1)
{
Quick(arr, left, par-1);
}
if (right > par + 1)
{
Quick(arr,par+1, right);
}
}
void Quick_sort(int* arr, int len)
{
Quick(arr, 0, len - 1);
}
2.快速排序的优化
因为快排数据越乱跑起来越快(数据越乱,就有更大的可能将数据均分为两个部分,时间复杂度接近 n*logn),所以优化的目的都是将数据尽可能地弄乱
2.1调用其他排序
当数据量较小时,例如 len<=100,可以不调用快排,直接调用直接插入排序或者冒泡排序(n比较小,n^2也不会太大)
void Quick_Sort(int *arr, int len)
{
//优化1:len如果小于100, 1000, 10000
if(len <= 100)
{
Bubble_Sort(arr, len);
return;
}
Quick(arr, 0, len-1);
}
2.2三数取中法
找到数组中最左边的数,最右边的数,和中间的数,将其按照下面顺序交换位置,目的还是为了让有序的数组变得无序。在调用Quick函数时先调用三数取中函数即可。

//优化2:三数取中法(写法非常的多)
void Get_ThreeNum_Mid(int *arr, int left, int right)
{
int mid = (left+right)/2;
if(arr[left] > arr[mid])//如果左值大于中值
{
int tmp = arr[left];
arr[left] = arr[mid];
arr[mid] = tmp;
}
//此时可以保证左值和中间的值 他俩较小的值 在左边
if(arr[mid] < arr[right])//前两个数的较大值和最右边的值比较
{
int tmp = arr[mid];
arr[mid] = arr[right];
arr[right] = tmp;
}
//此时可以保证 3个数的最大值 在中间
//而我们要的是 不大不小的值 (要么在左边,要么在右边)
if(arr[left] < arr[right])
{
int tmp = arr[left];
arr[left] = arr[right];
arr[right] = tmp;
}
//此时,就可以保证 不大不小的值在左边 而且还可以保证最大值在中间, 最小值在右边
}
2.3随机数法
利用随机数函数,将数组中的元素随机打乱,也是一种思路,了解即可。
3.快速排序——不使用递归
3.1基本思想
利用到了栈这一种数据结构,合理利用栈的特点,将每一次的 left 和 right 入栈,然后出栈调用分割函数。
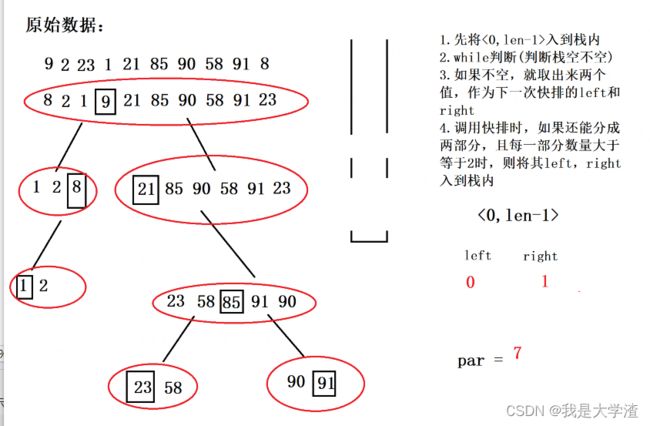
3.2非递归快排源代码
- 其中Partition和第一种方法相同
void Quick_Sort_Stack(int *arr, int len)
{
std::stack<int> st;
st.push(0);
st.push(len-1);
int left = 0;
int right = 0;
while(!st.empty())
{
right = st.top();
st.pop();
left = st.top();
st.pop();
int par = Partition(arr, left, right);
if(left < par-1)//左边部分至少有两个值
{
st.push(left);
st.push(par-1);
}
if(par+1 < right)//右边部分至少有两个值
{
st.push(par+1);
st.push(right);
}
}
}
3.3 性能分析
- 时间复杂度:最差O(n^2) 最优O(nlogn) 平均 O(nlogn)
- 空间复杂度:因为快排递归的时候,申请的辅助空间未释放,所以不是O(1),是O(logn)
- 稳定性:不稳定
- 特点:数据越乱排序越快
4.总结
快排效率较高,应用十分广泛,所以面试官经常考查快排,我们一定要掌握其原理和思想,了解其优化方法能熟练写出递归与非递归的代码。
