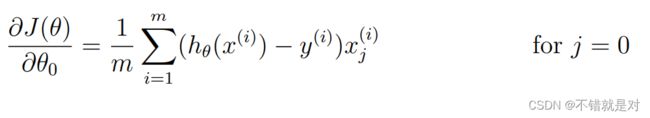吴恩达_Machine Learning_Programming Exercise 2: Logistic Regression
1、Logistic Regression
1.1 Visualizing the data
(1)打开 "plotData.m" ;
(2)输入:
% Find Indices of Positive and Negative Examples
pos = find(y==1); neg = find(y == 0);
% Plot Examples
plot(X(pos, 1), X(pos, 2), 'k+','LineWidth', 2, ...
'MarkerSize', 7);
plot(X(neg, 1), X(neg, 2), 'ko', 'MarkerFaceColor', 'y', ...
'MarkerSize', 7);完整代码如下:
function plotData(X, y)
%PLOTDATA Plots the data points X and y into a new figure
% PLOTDATA(x,y) plots the data points with + for the positive examples
% and o for the negative examples. X is assumed to be a Mx2 matrix.
% Create New Figure
figure; hold on;
% ====================== YOUR CODE HERE ======================
% Instructions: Plot the positive and negative examples on a
% 2D plot, using the option 'k+' for the positive
% examples and 'ko' for the negative examples.
%
% Find Indices of Positive and Negative Examples
pos = find(y==1); neg = find(y == 0);
% Plot Examples
plot(X(pos, 1), X(pos, 2), 'k+','LineWidth', 2, ...
'MarkerSize', 7);
plot(X(neg, 1), X(neg, 2), 'ko', 'MarkerFaceColor', 'y', ...
'MarkerSize', 7);
% =========================================================================
hold off;
end
结果如下:
1.2 Implementation
1.2.1 Warmup exercise: sigmoid function
Logistic Regression Model
(1) sigmoid function / logistic function : ![]()
(1)打开 "sigmoid.m" ;
(2)输入:
g = 1 ./ ( 1 + exp(-z) ) ;完整代码如下:
function g = sigmoid(z)
%SIGMOID Compute sigmoid function
% g = SIGMOID(z) computes the sigmoid of z.
% You need to return the following variables correctly
g = zeros(size(z));
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the sigmoid of each value of z (z can be a matrix,
% vector or scalar).
g = 1 ./ ( 1 + exp(-z) ) ;
% =============================================================
end
1.2.2 Cost function and gradient
Cost Function:
(1)打开 "costFunction.m" ;
(2)输入:
% J(theta)
h=sigmoid(X*theta);
first=y.*log(h);%第一项,点乘
second=(1-y).*log(1-h);%第二项,同样是点乘
J=-1/m*sum(first+second);%求和,代价函数
% 偏导数
grad=1/m*X'*(h-y);完整代码如下:
function [J, grad] = costFunction(theta, X, y)
%COSTFUNCTION Compute cost and gradient for logistic regression
% J = COSTFUNCTION(theta, X, y) computes the cost of using theta as the
% parameter for logistic regression and the gradient of the cost
% w.r.t. to the parameters.
% Initialize some useful values
m = length(y); % number of training examples
% You need to return the following variables correctly
J = 0;
grad = zeros(size(theta));
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta.
% You should set J to the cost.
% Compute the partial derivatives and set grad to the partial
% derivatives of the cost w.r.t. each parameter in theta
%
% Note: grad should have the same dimensions as theta
%
% J(theta)
h=sigmoid(X*theta);
first=y.*log(h);%第一项,点乘
second=(1-y).*log(1-h);%第二项,同样是点乘
J=-1/m*sum(first+second);%求和,代价函数
% 偏导数
grad=1/m*X'*(h-y);
% =============================================================
end
结果如下:
1.2.3 Learning parameters using fminunc
“fminunc” 只需要提供计算代价和梯度的函数costFunction.它会收敛到正确的最优参数,并且返回cost和θ
完整代码如下:
%% ============= Part 3: Optimizing using fminunc =============
% In this exercise, you will use a built-in function (fminunc) to find the
% optimal parameters theta.
% Set options for fminunc
options = optimset('GradObj', 'on', 'MaxIter', 400);
% Run fminunc to obtain the optimal theta
% This function will return theta and the cost
[theta, cost] = ...
fminunc(@(t)(costFunction(t, X, y)), initial_theta, options);
% Print theta to screen
fprintf('Cost at theta found by fminunc: %f\n', cost);
fprintf('Expected cost (approx): 0.203\n');
fprintf('theta: \n');
fprintf(' %f \n', theta);
fprintf('Expected theta (approx):\n');
fprintf(' -25.161\n 0.206\n 0.201\n');
% Plot Boundary
plotDecisionBoundary(theta, X, y);
% Put some labels
hold on;
% Labels and Legend
xlabel('Exam 1 score')
ylabel('Exam 2 score')
% Specified in plot order
legend('Admitted', 'Not admitted')
hold off;
fprintf('\nProgram paused. Press enter to continue.\n');
pause;结果如下:
decision boundary如下:
1.2.4 Evaluating logistic regression
index=find(sigmoid(X*theta)>=0.5);%找到>=0.5的
p(index)=1;2、Regularized logistic regression
2.1 Visualizing the data
2.2 Feature mapping
a 28-dimensional vector
2.3 Cost function and gradient
引入正则化之后,Logistic Regression的:
J(θ):
偏导数:
(1)打开 "costFunctionReg.m" ;
(2)输入:
theta_1 = [0;theta(2:end)]; % 把theta1拿掉,第一项不参与正则化;
reg = lambda/(2*m)*theta_1'*theta_1;
J=1/m*(-y'*log(sigmoid(X*theta))-(1-y)'*log(1-sigmoid(X*theta)))+reg;
grad=1/m*X'*(sigmoid(X*theta)-y)+lambda/m*theta_1;完整代码如下:
function [J, grad] = costFunctionReg(theta, X, y, lambda)
%COSTFUNCTIONREG Compute cost and gradient for logistic regression with regularization
% J = COSTFUNCTIONREG(theta, X, y, lambda) computes the cost of using
% theta as the parameter for regularized logistic regression and the
% gradient of the cost w.r.t. to the parameters.
% Initialize some useful values
m = length(y); % number of training examples
% You need to return the following variables correctly
J = 0;
grad = zeros(size(theta));
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta.
% You should set J to the cost.
% Compute the partial derivatives and set grad to the partial
% derivatives of the cost w.r.t. each parameter in theta
theta_1 = [0;theta(2:end)]; % 把theta1拿掉,第一项不参与正则化;
reg = lambda/(2*m)*theta_1'*theta_1;
J=1/m*(-y'*log(sigmoid(X*theta))-(1-y)'*log(1-sigmoid(X*theta)))+reg;
grad=1/m*X'*(sigmoid(X*theta)-y)+lambda/m*theta_1;
% =============================================================
end
2.3.1 Learning parameters using fminunc
同之前一样;
2.4 Plotting the decision boundary