堆&优先队列的底层实现
堆和优先对象
- 什么是优先队列
- 堆的相关概念
-
- 堆
- 向堆中添加元素(上浮 float up)
-
- 基础方法
- add(上浮)
- 图例
- 取出堆中优先级最高的元素
-
- 依次取出堆中的元素
- 下沉(swim)
- 图例
- 时间复杂度
什么是优先队列
普通队列的特点是:先进先出,而优先队列的出队顺序和入队顺序无关,只和优先级有关。当访问元素时,优先级最高的会被删除。可以使用堆这种数据结构作为优先队列的底层结构。
堆的相关概念
堆
1.堆可以看做是一棵树的数组对象,满足如下性质:
a.堆中的父亲结点总大于或等于其左右孩子结点的值
b.总是一棵完全二叉树
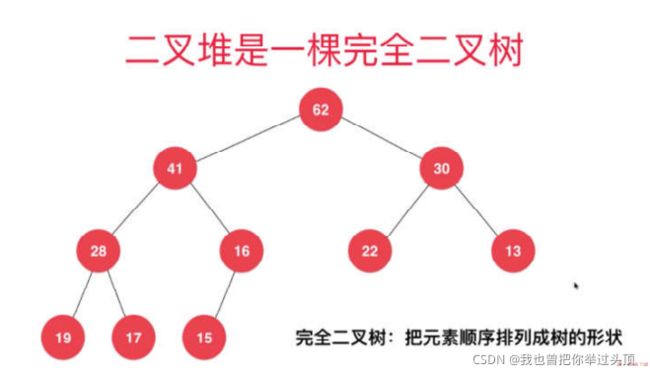
2.完全二叉树
二叉堆是一个完全二叉树
3.根据堆的性质可以得出一下结论
a.根节点没有父亲结点
b.除根节点之外的任意结点(i)的父亲结点的索引为: parent = i/2
c.任意结点的左孩子结点的索引为: leftIndex = 2 * i
d.任意结点的右孩子结点的索引为: rightIndex = 2 * i +1
上面的结论是根结点存储在索引为1的位置,如果根结点存储在索引为0的位置时,会得到:
a.parent = (i- 1)/2;
leftIndex = 2 * i + 1
rightIndex = 2 * I + 2;
向堆中添加元素(上浮 float up)
基础方法
概念已经知晓 咱们来看看怎么用代码实现堆(add元素)
优先构建两个变量分别储存数据和长度
private T[] data;//存储数据
private int size;//数据元素的个数
含参,无参构造方法
//无参构造方法
public MaxHeap(){
this.data = (T[])new Comparable[200];//转型
this.size = 0;
}
//含参赋值构造方法
public MaxHeap(T[] arr){
this.data = Arrays.copyOf(arr,arr.length);
this.size = arr.length;
}
下来一些很简单的方法 是否为空?返回长度;获取父节点;获取子节点…
/**
* 判断堆是否为空
* @return true为空 false不为空
*/
public boolean idEmpty(){
return this.size == 0;
}
/**
* 返回堆的长度
* @return int类型的长度
*/
public int getSize(){
return this.size;
}
获取父节点,要先对传进来的索引进行判断 :
- 如果是负数,则throw一个异常
- 如果是0,那么他是根节点,根节点没有父节点,所以返回 -1(自己定义的)
- 如果是非0正数,他的排序规则是父节点大于左右子节点,又因为他是一个满的二叉树,所以他的父节点是 左子节点/2 或者 (右子节点-1)/2(可以参考上面的图来想),总结一下就是 (index - 1) / 2
/**
* 获取父节点
* @param index 节点
* @return 父节点
*/
private int getParentIndex(int index) {
if (index < 0) {
throw new IllegalArgumentException("index is invalid!");
} else if (index == 0) {
return -1;
} else {
return (index - 1) / 2;
}
}
获取子节点:根据如何获取父节点可以推算(父节点2)就是左子节点,那么右子节点就是(父节点2)+1
/**
* 获得左孩子节点的索引
* @param index 索引
* @return 左节点
*/
public int getLeftChildIndex(int index){
if(index < 0){
throw new IllegalArgumentException("index not fushu");
}
return 2 * index + 1;
//右节点就是左节点加一
}
然后就是一个非常非常常见的重写toString方法
@Override
public String toString() {
StringBuilder sb = new StringBuilder("[");
int i = 0;
while (i < size) {
sb.append(this.data[i]);
if (i != size - 1) {
sb.append(",");
}
i++;
}
sb.append("]");
return sb.toString();
}
add(上浮)
添加元素很简单 无非就是将元素存入到我们自己定的data中
每增加一个元素size+1
但是重要的是添加进去的元素如何按照优先队列的特点排序好?这个操作我们称之为上浮,也叫浮动
public void add(T ele) {
// 1、 保存数据
data[this.size] = ele;
//2、更新size
size += 1;
//3、浮动操作
floatUp(size - 1);
//floatUp2(ele);
}
浮动:按照元素优先级(我们这里定义大小即为优先级 按照由大到小的方式排序)来排序,左右节点的优先级比父节点小 但是左右顺序无关 那么这里的灵魂就是两点
1. 循环比较子节点父节点优先级
2. 交换
第一种上浮操作:对比一次换一次
/**
* 上浮 将添加进来的元素移位到正确格式
* @param i
*/
private void floatUp(int i) {
// 1、获取父亲节点的索引
int curIndex = i;
int parentIndex = getParentIndex(curIndex);
// 2、比较优先级,如果比父亲节点的优先级高,就交换
while (curIndex > 0 && data[curIndex].compareTo(data[parentIndex]) > 0) {
swap(this.data, curIndex, parentIndex);//交换
curIndex = parentIndex; //交换了元素,那么也要交换索引
parentIndex = getParentIndex(curIndex);//获取父节点的方法 之前有写过
}
}
第二种上浮操作:循环对比,找到当前元素改在的优先级位置,然后再换
private void floatUp2(T ele) {
// 1、获取父亲节点的索引
int curIndex = this.size - 1;
int parentIndex = getParentIndex(curIndex);
// 2、比较优先级,如果比父亲节点的优先级高,就交换
while (curIndex > 0 && ele.compareTo(data[parentIndex]) > 0) {
//条件: 当前节点元素的优先级比父节点的优先级大
//执行操作: 当前节点的元素与父节点元素交换
data[curIndex] = data[parentIndex];
//当前节点的索引与父节点的索引交换
curIndex = parentIndex;
parentIndex = getParentIndex(curIndex);
}
data[curIndex] = ele;
}
swap 交换方法
很经典 a b temp的交换思想
temp=a;
a=b;
b=temp;
/**
* 交换操作
* @param arr
* @param curIndex
* @param changeIndex
*/
private void swap(T[] arr, int curIndex, int changeIndex) {
T temp = arr[curIndex];
arr[curIndex] = arr[changeIndex];
arr[changeIndex] = temp;
}
图例
1、添加元素52,添加到数组中索引为size的位置,然后更新size

2、从最后一个结点开始与父亲结节进行(优先级)比较,如果父亲结点的优先级低于当前结点,
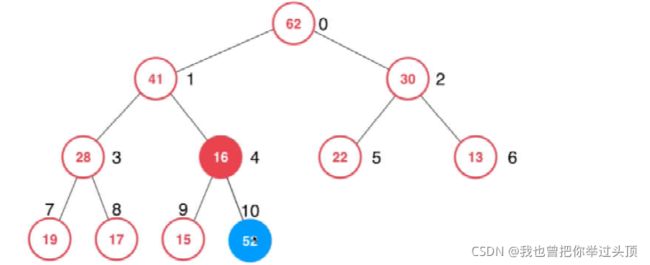
则进行交换

3、重复第二步操作,
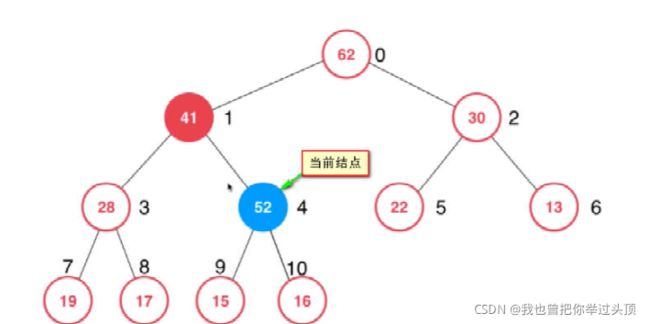
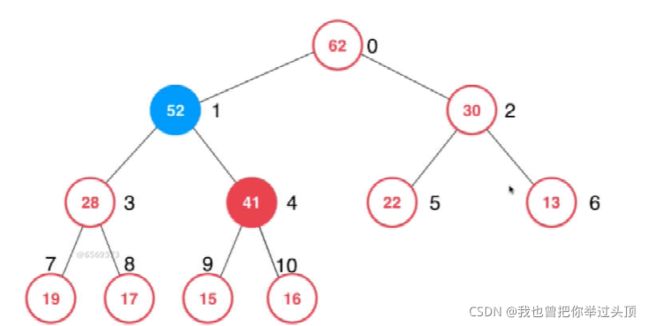
4、直至根节点或父亲结点的优先级高于当前结点

取出堆中优先级最高的元素
依次取出堆中的元素
取出元素并排序的几个步骤也很简单‘
1.保存根元素
2.先用length-1(最后一位)位置的元素替换根元素
3.size-1
* 4.下沉操作
public T removePriorityFirst() {
if (isEmpty()) {
throw new IllegalArgumentException("heap is null!");
}
// 1、保存根元素
T result = this.data[0];
// 2、用最后一个元素替换根元素
this.data[0] = this.data[this.size - 1];
// 3、更新size
this.size -= 1;
// 4、swim操作
swim();
return result;
}
// replace操作:取出优先级最高的元素,放入一个新元素---(让新元素替换索引为0的元素)
public void replace(T newEle) {
this.data[0] = newEle;
swim2();
}
下沉(swim)
// swim操作
private void swim() {
//先判断是否为空 为空不进行操作
if (isEmpty()) {
return;
}
//记录根节点
int curIndex = 0;
int leftIndex = getLeftChildIndex(curIndex);
int changeIndex = leftIndex;// 保存左右孩子优先级高的索引
// 有左孩子的条件: leftIndex < this.size
while (leftIndex < this.size) {
if (leftIndex + 1 < this.size && data[leftIndex].compareTo(data[leftIndex + 1]) < 0) {
//右孩子优先级>左孩子优先级
changeIndex = leftIndex + 1;
}
if (data[curIndex].compareTo(data[changeIndex]) > 0) {
break;
}
swap(this.data, curIndex, changeIndex);//交换
curIndex = changeIndex;
leftIndex = getLeftChildIndex(curIndex);
changeIndex = leftIndex;
}
}
private void swim2() {
if (isEmpty()) {
return;
}
T rootEle = this.data[0];
int curIndex = 0;
int leftIndex = getLeftChildIndex(curIndex);
int changeIndex = leftIndex;// 保存左右孩子优先级高的索引
// 有左孩子的条件: leftIndex < this.size
while (leftIndex < this.size) {
if (leftIndex + 1 < this.size && data[leftIndex].compareTo(data[leftIndex + 1]) < 0) {
changeIndex = leftIndex + 1;
}
if (rootEle.compareTo(data[changeIndex]) > 0) {
break;
}
data[curIndex] = data[changeIndex];
curIndex = changeIndex;
leftIndex = getLeftChildIndex(curIndex);
changeIndex = leftIndex;
}
data[curIndex] = rootEle;
}
图例

1、使用最后一个元素替换索引为0元素,更新size
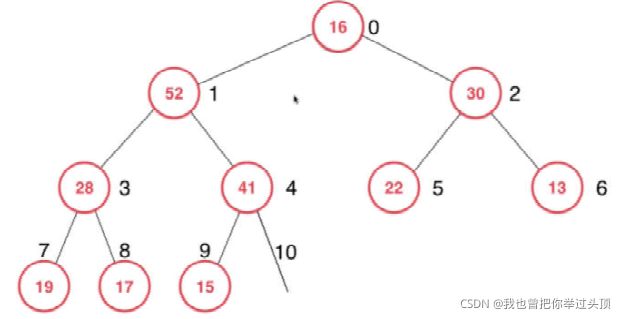
2、从索引为0的位置开始进行下沉操作
下沉操作:
1>找到当前结点左右孩子结点中优先级较高的结点

2>如果当前结点的优先级小于左右孩子结点中优先较高的结点,则进行交换
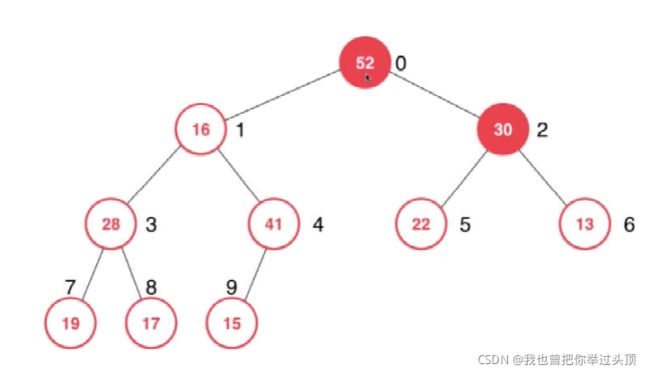
3>重复第2步操作
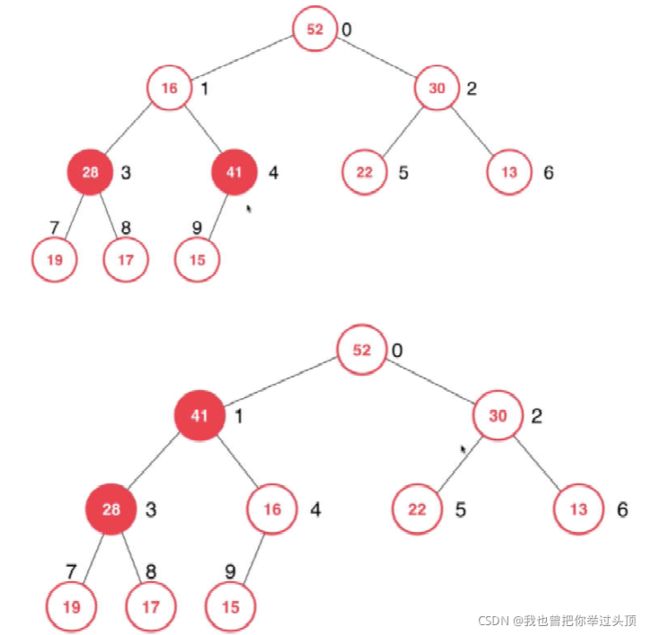
3、直至叶子结点或左右孩子结点中优先级较高结点小于当前结点的优先级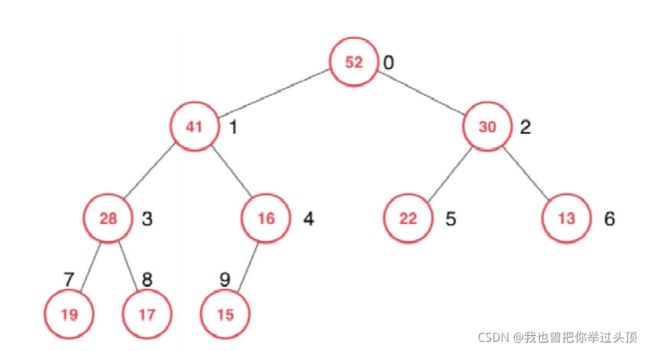
时间复杂度
从上面的分析图中,可以得出:无论进行上浮还是下沉操作,最多交换的次数为整棵树的高度h。每次重建意味着有一个节点出堆,所以需要将堆的容量减一。所以在每次重建时,随着堆的容量的减小,层数会下降,函数时间复杂度会变化。重建堆一共需要n-1次循环,每次循环的比较次数为log(i),则相加为:log2+log3+…+log(n-1)+log(n)≈log(n!)
假设一棵完全二叉树的高度为h,最后一个结点的父亲结点一定在h-1层,从h-1层开始进行下
沉操作,假设该层所有结点都要进行交换,那么每个结点交换的次数为1,所以总共交换了
12^(h-1-1)次依次类推假设h − 2层的结点都要进行交换,每个结点最多交换2次,总共交换的
次数为22 … … 到根节点交换的次数为 (h − 1) ∗ 2^(h-h)。
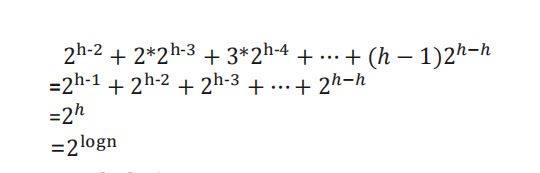
所以复杂度为 O(n)