IK学习笔记（1）——CCD IK

IK的概念

动力学分为正向动力学(FK)和反向动力学(IK)

其中正向动力学(FK)主要是通过父骨骼的变换，再由矩阵乘法得到子骨骼的最终变换

而反向动力学(IK)主要是通过子骨骼的变换，从而倒推出父骨骼应该怎么变换，而父骨骼产生变换之后，此时子骨骼会受到父骨骼变换的影响，子骨骼和目标点产生新的差距，此时需要迭代使用IK算法，直至趋近目标点

IK的应用

比如人物模型要抓住一个东西(如武器)的时候，我们一般是直接控制手部骨骼去抓东西，同时也希望骨骼间的结构产生“抓”这个动作的影响

比如人物模型站在不平坦的地面上时，我们需要调整脚上的骨骼，保证不会穿模，看起来脚是站在不平坦的地面上的，这时候我们也希望人物模型的腿部产生一定的影响

常见的IK算法

启发式法

启发式算法子家族实现了解决IK问题的简单方法，而不使用复杂的方程和计算。这些算法通常由简单的操作组成，以一种迭代的方式，逐渐推出IK解决方案。启发式IK算法具有较低的计算成本，因此通常很快就能得到最终的姿态，并且非常适合于简单的问题，特别是对于非人体测量骨骼（如蜘蛛、昆虫）。它们的主要局限之一是，即使满足了所有的关节约束，它们也会产生非自然或生物力学上不可行的动作和手势。启发式解算器不考虑附近关节之间的时空修正，因为它们独立地处理每个关节的约束，而不考虑全局约束。

CCD IK(循环坐标下降逆动态学)

原理：一次转换一个关节变量来最小化位置和姿态误差。

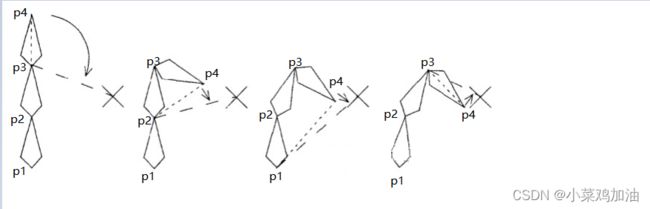
策略思路：每个骨骼都以自身轴点到尾叶子节点的方向旋转到自身轴点到目标点方向，开始趋近

举例说明：

[P3,P4]：首先计算[P3,P4]的向量与[P3,目标点]的向量，得出向量之间的夹角旋转角度，此时将[P3,P4]进行角度旋转

[P2,P3]：计算[P2,P4]的向量与[P2，目标点]的向量，得出向量之间的夹角旋转角度，此时将[P2,P3]进行角度旋转，同时注意子骨骼会受到该旋转的影响产生偏移

[P2,P1]：计算[P1,P2]的向量与[P1,目标点]的向量，得出向量之间的夹角旋转角度，此时将[P2,P1]进行角度旋转，同时注意子骨骼会受到该旋转的影响产生偏移

进行了这一次迭代之后可以发现P4此时和目标点又会产生旋转角度的偏差，因此可以继续进行迭代，当迭代到一定次数之后，就会逼近目标点

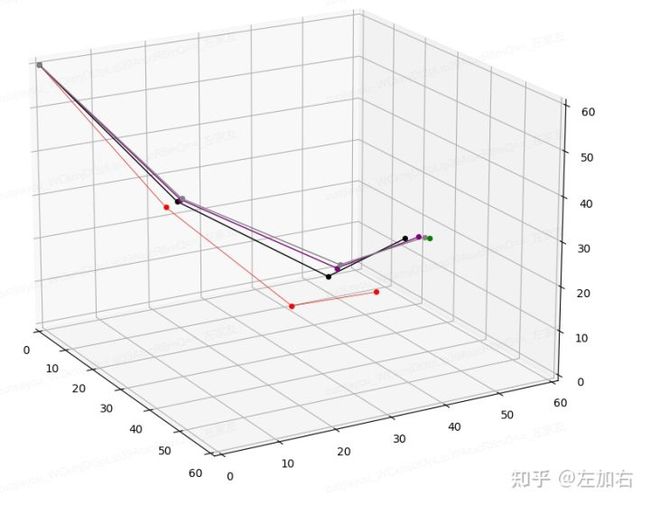
• 多次迭代图

• 骨骼演算核心参考代码

for (int i = bones.Length - 2; i > -1; i--) {
	// Slerp if weight is < 0
	//CCD tends to overemphasise the rotations of the bones closer to the target position. Reducing bone weight down the hierarchy will compensate for this effect.
	float w = bones[i].weight * IKPositionWeight;

	if (w > 0f) {
		Vector3 toLastBone = bones[bones.Length - 1].transform.position - bones[i].transform.position;
		Vector3 toTarget = targetPosition - bones[i].transform.position;
						
		// Get the rotation to direct the last bone to the target
		Quaternion targetRotation = Quaternion.FromToRotation(toLastBone, toTarget) * bones[i].transform.rotation;
						
         if (w >= 1) bones[i].transform.rotation = targetRotation;
			else bones[i].transform.rotation = Quaternion.Lerp(bones[i].transform.rotation, targetRotation, w);
		}
}

参考文章

https://blog.csdn.net/f980511/article/details/123316988

https://zhuanlan.zhihu.com/p/499405167

https://zhuanlan.zhihu.com/p/469221237

https://www.twblogs.net/a/5ee13245cd139eebd77e9dd0/?lang=zh-cn