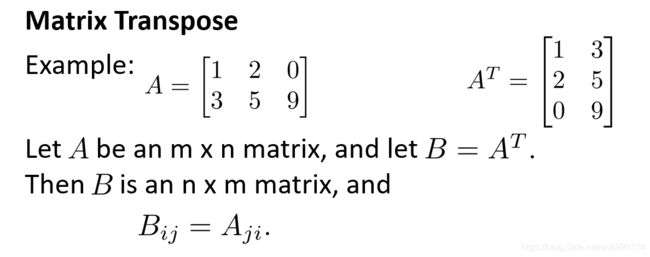《吴恩达机器学习》3 线性代数回顾
线性代数回顾
- 前言
-
- 一、矩阵和向量
-
-
- 1、张量
- 2、标量
- 3、矩阵
- 4、向量
-
- 二、矩阵和向量运算
-
-
- 1、矩阵加法
- 2、矩阵与标量乘除法
- 3、矩阵与矩阵乘法(重要)
-
- 三、矩阵运算特性
-
-
- 1、不满足乘法交换律
- 2、满足乘法结合律
- 3、单位矩阵
- 4、特殊技巧
-
- 四、逆矩阵和转置
-
-
- 1、逆矩阵
- 2、转置
-
- 总结
前言
线性代数的知识在机器学习中是非常重要的,几乎所有的运算都是基于矩阵(Matrix)、向量(Vector)的运算,因此打好线性代数的基础(不求精通,只要基本的运算既可)是学习好Machine Learning的关键。
一、矩阵和向量
其实很多教程都有介绍基本的线性代数概念,但是我看了很多觉得都解释得不够好。至今看得最好的解析是《Python深度学习》这本书,书由Keras创作者和Google AI研究员FrançoisChollet 撰写,通过直观的解释和实际例子构建您的理解。我分享中有这本电子书籍可以下载,有需要的同学可以去下载 (当然有条件的还是购买正版书籍较好)
1、张量
张量(tensor),google出的机器学习框架tensorflow就以张量来命名,可见这个概念是多么重要。
张量这一概念的核心在于,它是一个数据容器。它包含的数据几乎总是数值数据,因此它
是数字的容器。你可能对矩阵很熟悉,它是二维张量。张量是矩阵向任意维度的推广[注意,
张量的维度(dimension)通常叫作轴(axis)]。
可见张量就是数据容器,存储着机器学习的数据。几乎所有的数据都要转成张量才能进行计算,比如图片,语音,一段话等。
2、标量
标量指的是一个数值,比如[3],在线性代数中它就是一个标量
3、矩阵
矩阵就是二维张量(2D 张量),在计算机中可以看成是二维数组,下面是一个矩阵Aij其中i = 4, j = 2,表示这是一个4x2的矩阵,再比如A12 = 191,表示第一行(raw)第二列(column)的值是191

4、向量
向量就是一维张量(1D 张量),我们在机器学习中常说的向量都是列向量,特别对于以后的计算这个很重要。当然你可以可以看出它是只有一列的矩阵,这个是一样的概念,我们通常用小写字母a,b,c,d表示,如y2 = 232,表示第二行的值是191
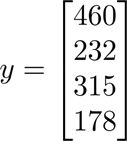
二、矩阵和向量运算
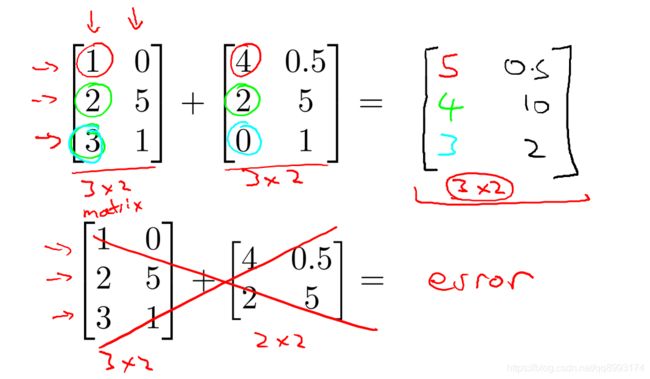
1、矩阵加法
注意只有同维度的矩阵才能相加,比如3x2的矩阵可以加上3x2的矩阵,但是3x2的矩阵加上2x2的矩阵是没有意义的
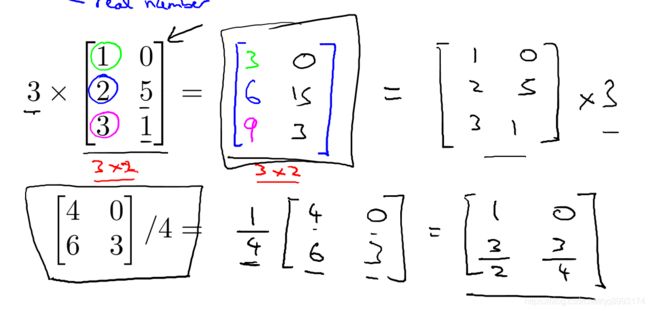
2、矩阵与标量乘除法
很简单就是与标量与每个数值相乘得到结果,与标量相乘不会改变本身的维度
3、矩阵与矩阵乘法(重要)
AxmxBmy = Cxy
矩阵中必须m = m才成立,即A矩阵的列等于B矩阵的行,运算后的矩阵C的行等于A的行,列等于B的列
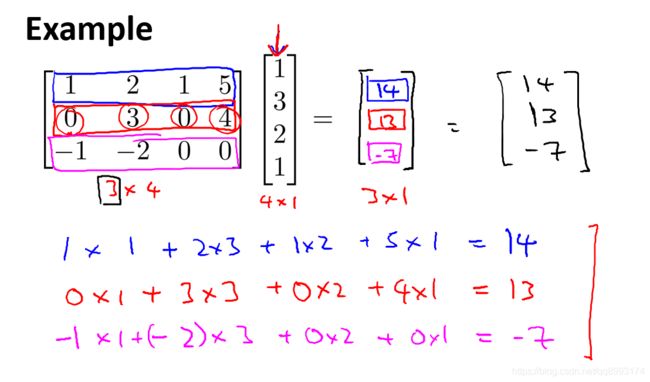
下面是一个矩阵与向量相乘的例子,向量就是列数是1的矩阵
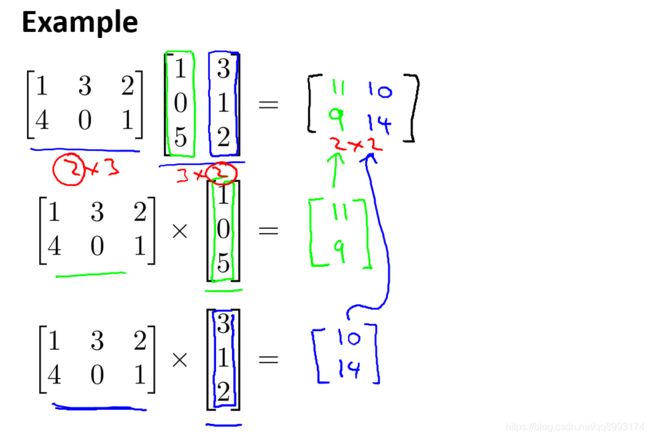
下面是矩阵与矩阵相乘的例子
三、矩阵运算特性
1、不满足乘法交换律
如Aij x Bjk ≠ Bjk x Aij,如矩阵的乘法必须满足A列等于B行,反过来就不一定了,所以不满足乘法交换律
2、满足乘法结合律
如(A x B) x C = A x (B x C),记住即可。可以自己推导以下是成立的
3、单位矩阵
单位矩阵即对角线元素是1的矩阵,一个矩阵乘以单位矩阵等于矩阵本身

4、特殊技巧
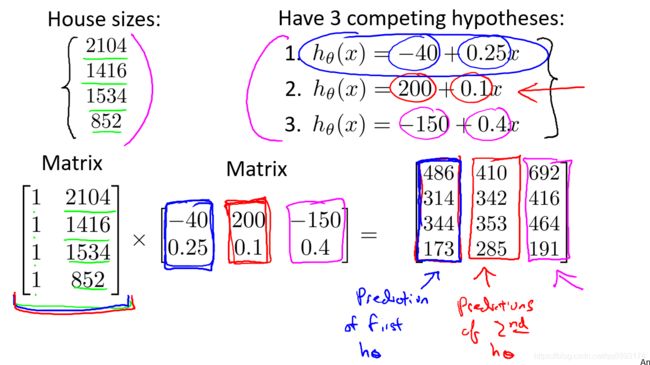
如下图示这个技巧挺好玩的,我们要得到右边公式的值,可以把我们的输入值转为一个矩阵,这样乘以因斜率和截距组成的矩阵,即可得出我们的目标值。
这个在计算机中有个好处就是我们可以只写一行代码计算出结果,如用Python编程时很快得出结果,而不是搞一个for循环去遍历所有的值去做运算
A = [[1, 2104],[1, 1316],[1, 1534],[1, 852]]
B = [[-40, 200, -150],[0.25, 0.1, 0.4]]
C = A x B
四、逆矩阵和转置
1、逆矩阵
设A是数域上的一个n阶矩阵,若在相同数域上存在另一个n阶矩阵B,使得: AB=BA=E ,则我们称B是A的逆矩阵,而A则被称为可逆矩阵。注:E为单位矩阵。
我们先来了解方阵,方阵就是行和列相等的矩阵。逆矩阵的概念就是当有一个方阵AxB = I,其中I是单位矩阵,那么B就是A的逆矩阵,记做AT

2、转置
总结
以上是《吴恩达机器学习》系列视频 线性代数回顾 一些笔记和见解,以便后续学习和查阅。