吴恩达机器学习视频课笔记【第4-5章】

目录

4 多变量的线性回归

4.1 多元梯度下降法

一些notation

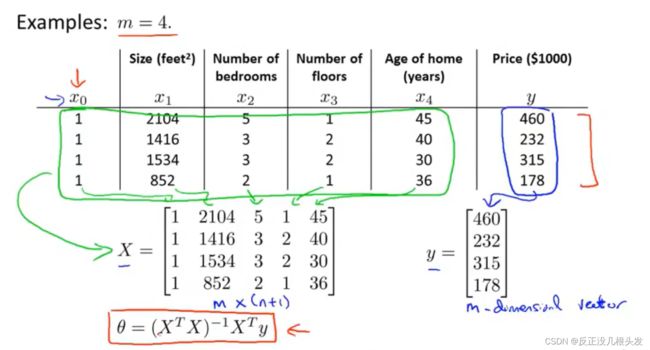
例子：预估房价

多元线性回归方程

关于多元线性回归

多元梯度下降法

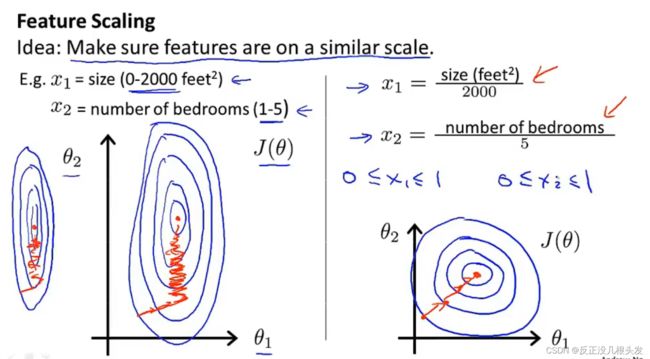
4.2 特征缩放

scale缩放

归一化(Mean normalization)

4.3 学习率(Learning rate)

4.4 特征和多项式回归

特征的选择

多项式回归

4.5 正规方程(Nomal equation)

1、直观上找到θ的最小值

2、正规方程(重点)

3、梯度下降法 和 正规方程法 的优缺点

补充：正规方程在不可逆的情况下的解决办法

5 Octave基本操作

一些函数

使用Octave画图

控制语句

向量化（重点）

---

4 多变量的线性回归

4.1 多元梯度下降法

一些notation

n：feature的个数

x(i)：第i个training example的features（特征向量）

​ 若有n个特征(eg：房子大小，房间数目，楼层数，房子年龄)，即为n维向量

xj(i)：第i个训练样本中第j个特征的值

例子：预估房价

 

多元线性回归方程

 

关于多元线性回归

 

多元梯度下降法

 

4.2 特征缩放

不需要太精确，相似的范围都可以，只是为了让梯度下降能够运行得更快

特征缩放的作用：将梯度下降的速度变得更快，收敛所需的迭代次数更少

scale缩放

make sure features are on a similar scale

更快通过梯度下降法找到一条更直接的路径通向全局最小（使得梯度下降法更快收敛）

通常做法：将特征的取值放在 -1<= xi <= 1

​ (我们默认 x0 = 1，其他的x可能要除以不同的数以达到这个范围，接近这个范围也行)

 

归一化(Mean normalization)

xi ---> xi-μi 使得特征的均值为0

μi为原xi的平均值

si为原xi范围：最大值 - 最小值 （或者是标准差σ---方差的算术平方根）

4.3 学习率(Learning rate)

要确保梯度下降正常工作

 

若出现以下情况，说明梯度下降没有正常工作

1、可能是学习率设置的太大导致的---可能不会收敛

2、可能是学习率设置的太小导致的---收敛得很慢

 

学习率的选择：每隔10倍取一个值

α：0.001-->0.01-->0.1-->1

实际上的取值可能如下：

0.001-->0.003-->0.01-->0.03-->0.1-->0.3-->1-->...

最后取最大值，或者比最大值略小的合理的值

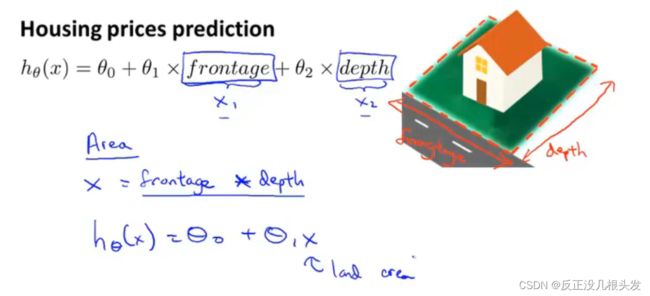
4.4 特征和多项式回归

特征的选择

例子：预测房价

有两个特征：临街宽度 和 房子的深度

可以化为一个特征：房子的面积 = 临街宽度 * 房子深度

 

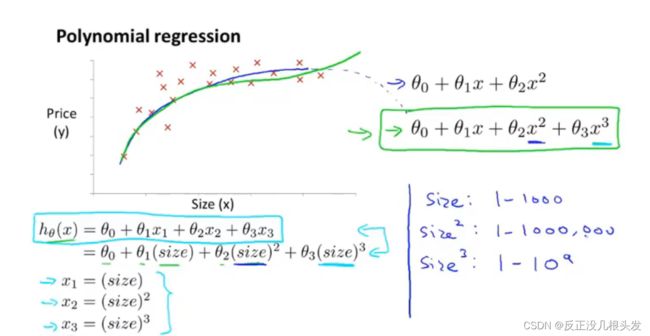
多项式回归

多次幂 简化为 一次幂 （一定要使用特征缩放）

 

选择合适的特征，构造多项式

 

4.5 正规方程(Nomal equation)

直接得到最优的θ，而不需要多次迭代找到最小的θ

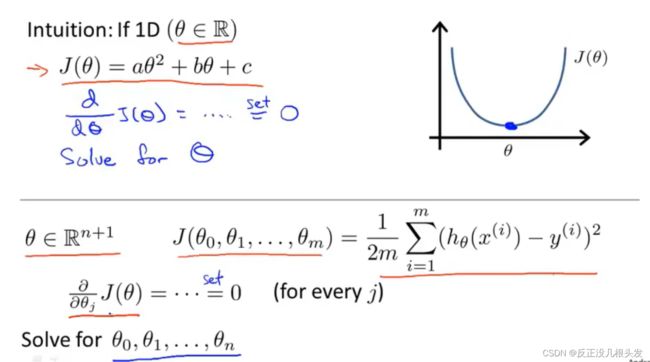
1、直观上找到θ的最小值

 

2、正规方程(重点)

θ = ( XTX)-1XTy

 

m个样本，每个样本有n个特征

 

Octave：pinv(x' * x) * x' * y

pinv表示求逆矩阵，x'表示x的转置

正规方程可以求出最小的θ

3、梯度下降法 和 正规方程法 的优缺点

使用正规方程法，就不需要特征缩放，

若使用梯度下降法，则需要进行特征缩放

当特征的个数n很多时，正规方程法 效率不太高（一般：n > 10000）

 

(分类算法，logistic 回归算法 不适合用正规方程法，仍使用梯度下降法)

补充：正规方程在不可逆的情况下的解决办法

通常不会出现这种情况，在Octave中使用pinv()可得到伪逆矩阵，即使X'X不可逆，也会出现正确结果

出现不可逆的原因：

1、包含了多余的特征（冗余）

2、太多的特征，而样本少 --- 解决方法：删除某些特征，或者正则化

5 Octave基本操作

一些函数

exit/quit：退出Octave

pwd：显示当前绝对路径

randn()：生成一组符合高斯分布（正态分布）的随机数

rand()：生成一组随机数

hist(w)：绘制变量w的直方图

参考octave的安装与使用_每昔的博客-CSDN博客_octave

关于矩阵的一些操作

 

ceil()：向上取整

floor()：向下取整

pinv()：取伪逆

使用Octave画图

plot()

subplot(m,n,i)：把画布分成m*n块，使用第i块

 

hold on ：在新画布上画图，不更新原画布

xlabel('...')：给x轴命名

ylabel('...')：给y轴命名

title('...')：给图形命名

legend()：文字说明，图例

print -dpng '图片名称' ：将图形以png格式保存在当前目录下

axis([ ... ])：设置坐标轴范围

close：关闭图形

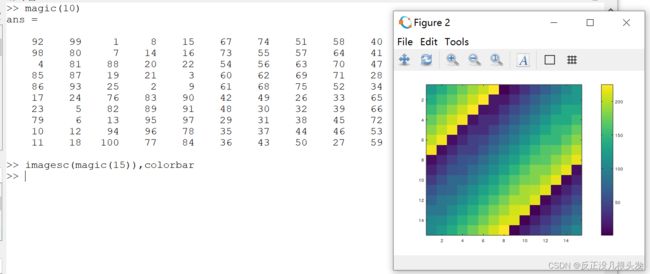
绘画矩阵：

imagesc()

colorbar：色条

 

colormap gray：设置为灰色

 

控制语句

for循环

 

或者

 

while循环

 

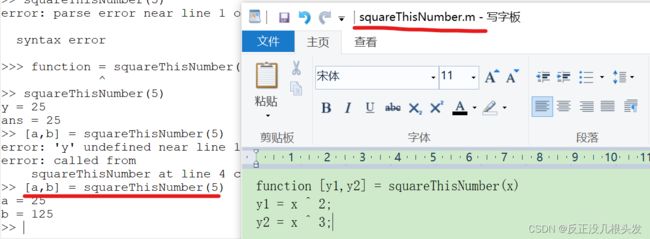
读取当前目录下的函数文件，返回值可以有多个

 

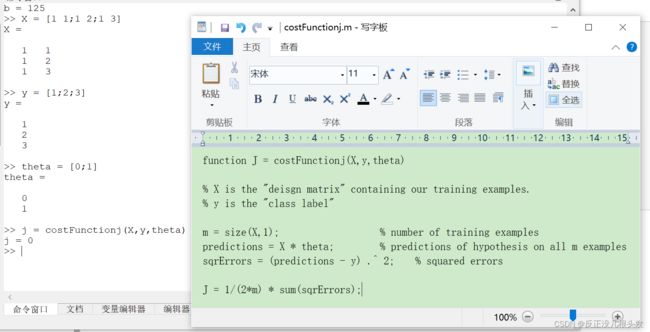
代价函数的实现

function J = costFunctionj(X,y,theta)
​
% X is the "deisgn matrix" containing our training examples.
% y is the "class label"
​
m = size(X,1);          % number of training examples
predictions = X * theta;        % predictions of hypothesis on all m examples
sqrErrors = (predictions - y) .^ 2; % squared errors
​
J = 1/(2*m) * sum(sqrErrors);

 

向量化（重点）

简化代码

Octave中

 

C++实现

 

向量化