多元线性回归，参数估计，模拟，最小二乘法，极大似然估计，matlab

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

多元线性回归参数估计课题，方法
最小二乘法
极大似然估计
这两个方法差不多所以放在一个文章里
本文更多记录代码，原理找其他文章
matlab语言

---

一、多元线性回归

参考高中回归方程中求a,b的情况

多元就是多个x,求x前面的系数，和常数项（本文中求没求常数项忘记了，有兴趣的试试，给我说啊）

我记得这篇文章我好像有用模拟，多次实验得到的数据均值来对比

得到的模拟值（msigma,mbeta）求平均值（mean）均值误差（Bias）标准差（SD），95%分位数和5%分位数

二、最小二乘法，极大似然估计

原理：建议看其他文章（打字太麻烦了）
极大似然估计：emm忘记了(好像是有个求导，求对数，令=0，忘记了，改天翻书看看再改）

三、使用步骤

1.产生数据（和上一篇文章代码一样）

代码如下（示例）：

%产生xy数据
function [y,x]=gendata(n,p,beta)
x=normrnd(0,1,n,p);%x是n*p矩阵
muy=x*beta';%乘，a的列数=b的行数,pinv矩阵的逆
y=normrnd(muy,1,n,1);%y是n*1矩阵
end

2.方法

代码如下（示例）：

%最小二乘法参数估计OLES
function [mbeta,msigma]=olse(n,p,x,y)
a=x'*x;   %x是n*p
mbeta=inv(a)*x'*y;   %mbeta是p*1矩阵 y是n*1
SSE=sum((y-x*mbeta).^2); %.^按元素求幂（结果应该是值）1*1
msigma=1/(n-p)*SSE; 
mbeta=mbeta';
msigma=msigma';
end

%极大似然估计MLE
function [mbeta,msigma]=MlE(n,p,x,y)
a=x'*x;   %x是n*p
mbeta=inv(a)*x'*y;  %mbeta是p*1(4*1)矩阵 y是n*1(100*1)
SSE=(y-x*mbeta)'*(y-x*mbeta);  %.^按元素求幂（结果应该是值）1*1
msigma=1/n*SSE;
mbeta=mbeta';
msigma=msigma';
m=[mbeta,msigma];
end

3.完整代码

没写完但求参数够了，对比没写

%最小二乘法估计法模拟参数与真值的bias,
%参数模拟，求标准差，均方差，5%，95%，均值差对比
%循环100次
n=100;
p=4;
beta=[1,-sqrt(3)/3,sqrt(2),0.8];% beta=[1.0000,-0.5774,1.4142,0.8000]
sigma=1;
result1=zeros(100,5);
true=[beta,sigma];
for i=1:100
     [y,x]=gendata(n,p,beta);  %第一步：产生数据
     [mbeta,msigma]=olse(n,p,x,y);%第二步：求模拟值
     result1(i,1:4)=mbeta;
     result1(i,4:5)=msigma;
end
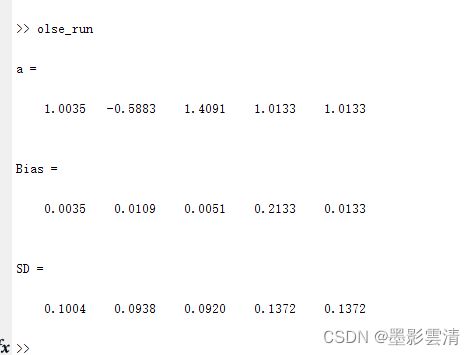
a=mean(result1,1)%按照列求均值
Bias=abs(a-true) %均值误差Bias
SD=std(result1)%标准差
%95%分位数
%5%分位数

%极大似然估计法模拟参数与真值的bias,
%参数模拟，求标准差，均方差，5%，95%，均值差对比
%循环100次
n=100;
p=4;
beta=[1,-sqrt(3)/3,sqrt(2),0.8];% beta=[1.0000,-0.5774,1.4142,0.8000]
sigma=1;
result1=zeros(100,5);
true=[beta,sigma];
for i=1:100
     [y,x]=gendata(n,p,beta);  %第一步：产生数据
     [mbeta,msigma]=MlE(n,p,x,y);%第二步：求模拟值
     result1(i,1:4)=mbeta;
     result1(i,4:5)=msigma;
end
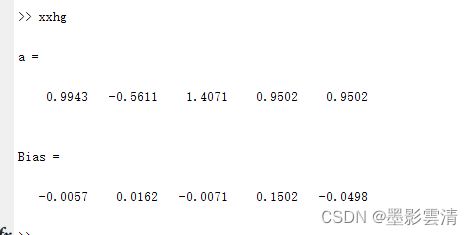
a=mean(result1,1)%按照列求均值
Bias=a-true  %均值误差Bias

---

总结

后续再补吧，代码保存好了，下次上机再看吧

以上代码有问题，直接留言，刚好当提前答辩了，一个人找问题不好找，人多了，问题多的很