多项式回归模型

目录

前置知识

Numpy c_函数

问题引入

多项式回归函数

核心思路

示例

数据生成

转化多项式回归训练集

预测和绘图

 特征缩放

补充：关于多项式的次数选择

---

 

多项式回归虽然不再用直线拟合，但也是线性回归的一种，可以转化为多元线性回归，利用多元线性回归的函数解决。所以请确保熟悉多元线性回归相关知识点：多元线性回归模型_Twilight Sparkle.的博客-CSDN博客

 在学习多项式回归之前，你可能需要先了解以下内容：

前置知识

多项式_百度百科 (baidu.com)

多项式函数_百度百科 (baidu.com)

Numpy c_函数

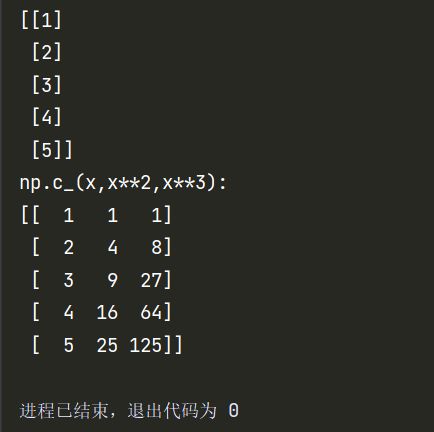
该函数可以实现按列拼接矩阵，具体用法：

import numpy as np

x = np.array([[1],[2],[3],[4],[5]])
print(x)
X = np.c_[x,x**2,x**3]
print("np.c_(x,x**2,x**3):")
print(X)

问题引入

现实生活中呈（狭义）线性关系的事物联系很少，绝大部分都是（狭义）非线性的，即呈曲线形式的关系。所以我们需要引入多项式回归来更好的拟合数据。

多项式回归函数

多项式回归又分为多元多项式回归和一元多项式回归：

一元多项式：

多元多项式：这里只举二元二次多项式

不管它是什么多项式，在处理上不同的地方都只是在数据预处理上，核心方法不变。这里为了绘图，以一元多项式进行讲解。

核心思路

令,于是多项式回归转化成了多元线性回归。然后套用多元线性回归的函数求解向量和常量即可。

示例

注：以下函数均来自上篇文章（多元线性回归）

Zscore()：Z-score标准化

gradient_descent()：拟合回归函数,为了更好用，把初始化w和b的函数重新写了一下。

 gradient_descent()初始化w，b修改：

    m, n = X.shape
    # initialize parameters
    init_w = np.zeros(n)
    init_b = 0

数据生成

以下代码可以生成该示例的训练集数据：

def data_generation():
    '''
    :return:
        X: 自变量训练集（矩阵）
        Y: 应变量训练集（一维）
    '''
    x = np.arange(0,40,1)
    y = 0.25*x**2-0.20*x**3+0.0055*x**4
    # 要将X训练集转化为(m,n)的矩阵，即m个例子，n个特征，现在是一元，所以只有一列
    x = x.reshape(-1,1)
    # 生成随机数，稍微打乱y
    np.random.seed(1)
    y = y + np.random.random(40)*120
    return x,y

转化多项式回归训练集

def x_transform(x):
    '''
    :param x:转化前的X训练集
    :return: 转化后的X训练集
    '''
    X_train = np.c_[x,x**2,x**3,x**4]

    return X_train

预测和绘图

if __name__ == '__main__':
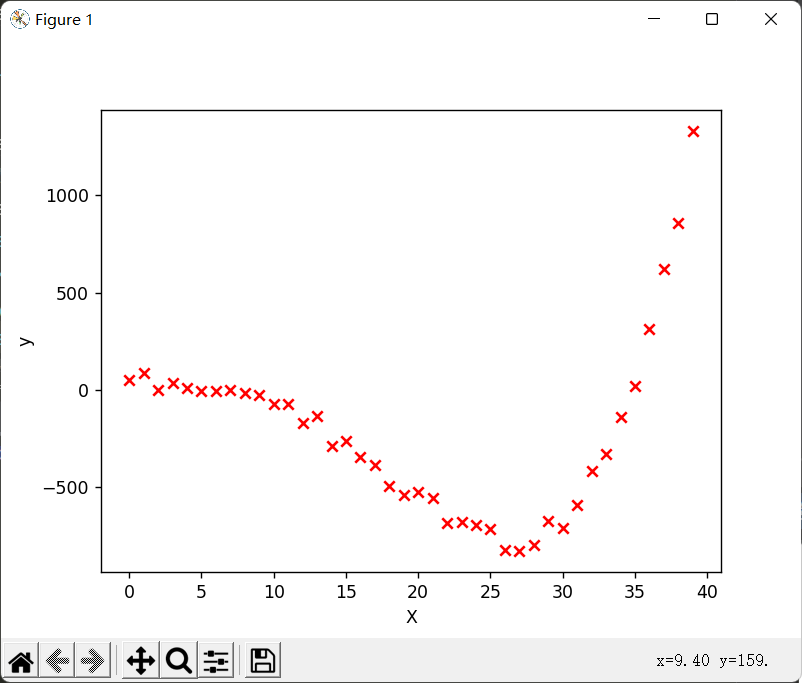
    # 生成数据并绘制训练集图
    x_train,y_train = data_generation()
    plt.scatter(x_train,y_train,marker='x',c='r',label = 'Actual Value')
    plt.xlabel("X")
    plt.ylabel("y")
    # plt.show()
    # 将x训练集转化为多元线性训练集
    x_train_transform = x_transform(x_train)

    # 预测并绘图
    model_w,model_b = gradient_descent(x_train_transform,y_train,alpha=0.000000000003,num_iters=100000)
    plt.plot(x_train,np.dot(x_train_transform,model_w) + model_b,label="Predicted Value")
    plt.legend()
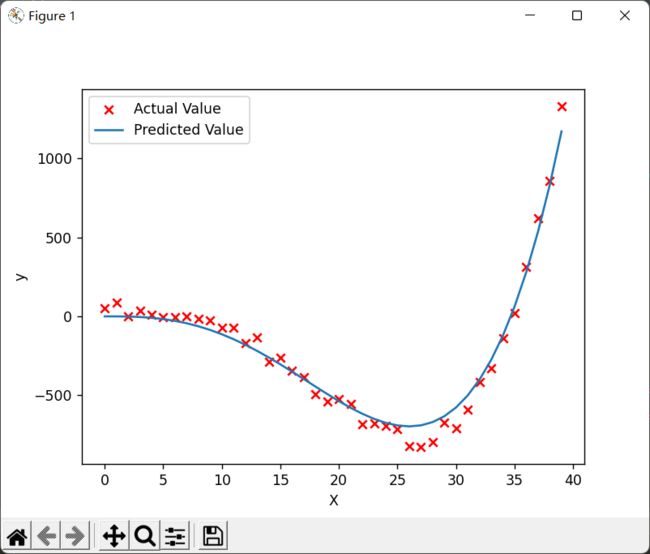
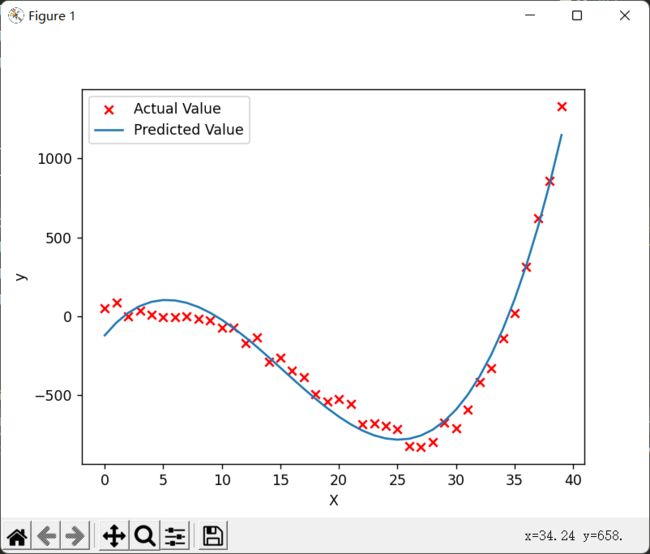
    plt.show()

 结果：

 特征缩放

因为转化为多元一次回归后，会发现每个特征的范围差的特别大（比如和），为了照顾取值大的特征，学习率必须设置的非常小，所以梯度下降特别慢。这时，就要用到之前说过的特征缩放了。

特征缩放后的预测和绘图：

    # 将x训练集转化为多元线性训练集
    x_train_transform = x_transform(x_train)
    x_train_transform, mu, sigma = Zscore(x_train_transform)
    # 预测并绘图
    model_w,model_b = gradient_descent(x_train_transform,y_train,alpha=0.5,num_iters=10000)
    plt.plot(x_train,np.dot(x_train_transform,model_w) + model_b,label="Predicted Value")
    plt.legend()
    plt.show()

 对比学习率和迭代次数，根本不是一个级别的。而且在更短时间内模拟的更好：

 所以特征缩放很重要！！

补充：关于多项式的次数选择

次数的选择： 多项式函数有多种，一般来说，需要先观察数据的形状，再去决定选用什么形式的多项式函数来处理问题。比如，从数据的散点图观察，如果有一个“弯”，就可以考虑用二次多项式；有两个“弯”，可以考虑用三次多项式；有三个“弯”，则考虑用四次多项式，以此类推。 当然，如果预先知道数据的属性，则有多少个

虽然真实的回归函数不一定是某个次数的多项式，但只要拟合的好，用适当的多项式来近似模拟真实的回归函数是可行的。

原文链接：多项式回归详解 从零开始 从理论到实践

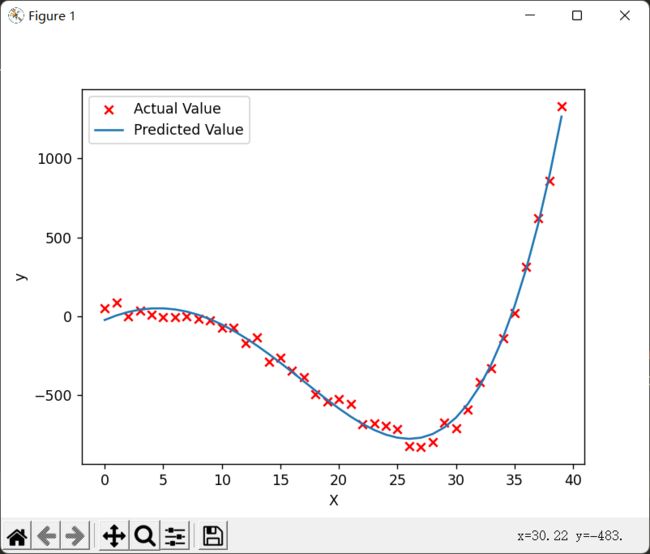
 稍微尝试了一下这个规律，刚才我构造的函数虽然是四次方的，但是只用三次的多项式也可以模拟出来效果较好的：

X_train = np.c_[x,x**2,x**3]