数据结构---内部排序

目录

一、概述

1.排序算法的稳定与不稳定

2.内部排序和外部排序

3.排序方法的效率分析

二、插入排序

1.直接插入排序

2.折半插入

3.希尔排序

三、快速排序

1.冒泡排序

2.快速排序

四、选择排序

1.简单选择排序

2.树形选择排序

3.堆排序

五、归并排序

1.归并的定义

2.（2路）归并排序思想

3.K-路归并

六、基数排序

1.基数排序的起源

2.链式基数排序

3.算法分析

七、内部排序方法的比较

---

一、概述

1.排序算法的稳定与不稳定

1.1稳定：在排序前后，含相等关键字的记录的相对位置保持不变

1.2不稳定：相等关键字的记录的相对位置有可能改变

2.内部排序和外部排序

2.1内部排序：在排序过程中，只使用计算机的内存存放待排序记录

2.2排序期间文件的全部记录不能同时存放在计算机内存中，要借助计算机的外存才能完成排序

2.3内外存之间的数据交换次数是影响外部排序速度的主要因素

3.排序方法的效率分析

3.1时间复杂度：关键字的比较次数和记录移动次数

3.2空间复杂度：执行算法所需的附加储存空间

3.3稳定算法和不稳定算法

二、插入排序

1.直接插入排序

1.1直接插入排序从第二个记录开始（第一个记录为空、监视哨）

1.2直接插入排序第i趟后序列的前i+1个记录是有序的（每一趟都让后面的一个元素排序到前面构成新的有序序列）

1.3插入排序的思想：

1.3.1第一个记录是有序的

1.3.2从第二个记录开始，按关键字的大小将每个记录插入到已排好序的序列中

1.3.3一直进行到第n个记录

1.3.4整个排序过程需要进行比较、后移记录、插入适当位置。从第二个记录到第n个记录共需n-1趟

1.4直接插入排序原序列呈正序排列时，最省时间（相对的：原序列为反序时最费时间）

1.5直接插入排序是最稳定的排序方法

1.6时间复杂度：平均O(n^2)；空间复杂度：O(1)

1.6.0时间复杂度：最好情况:比较O(n),移动O(1);最坏情况:比较O(n2),移动O(n2);平均O(n2)

2.折半插入

2.1在直接插入排序进行第i个元素时，利用折半查找找到插入的位置

2.2折半插入排序是稳定的排序方法

2.3时间复杂度：O(n^2)；空间复杂度：O(1)

2.3.0时间复杂度：最好情况:比较O(n),移动O(1);最坏情况:比较O(log2(n!)),移动O(n^2);平均O(n^2)

3.希尔排序

3.1希尔排序的思想

3.1.1对待排记录序列先作“宏观”调整，再作“微观”调整

3.1.2“宏观”调整：“跳跃式”插入排序

3.2希尔排序概述

3.2.1将记录序列分成若干子序列，分别对每个子序列进行插入排序（将n个记录分为d个子序列）

3.2.2d为增量，它的值在排序过程中从大到小逐渐缩小，直至最后一趟排序减为1

3.3在增量为d时，希尔排序从d+1个排序开始

3.4希尔排序的最终增量为1（直接插入排序）

3.5希尔排序是不稳定得排序方法

3.6希尔排序得时间复杂度：平均O(n^1.3)到平均O(n^1.5)

3.7希尔排序得空间复杂度：O(1)

三、快速排序

1.冒泡排序

1.1冒泡排序一趟后最大元素沉底，最大元素位于它最终的位置上，总共需要n-1趟

1.2基本思想：从第一个记录开始，两两比较交换，一趟比较结果后，关键字最大的记录放到最后一个位置，最小的则上浮一个位置（n个记录比较n-1遍）（如果某趟后序列没有变化，就表示已经排好了）

1.3.1冒泡排序的结束条件为：最后一趟没有进行“交换记录”

1.3.2一般情况下，每经过一趟“冒泡”，“i减1”，但并不是每趟都这样

1.4冒泡排序是稳定的排序方法

1.5时间复杂度：最好情况：比较O(n), 移动O(1)最坏情况：比较O(n2), 移动O(n2)平均情况：O(n2)

1.6空间复杂性O(1)

2.快速排序

2.1基本思想：（分治算法）找一个记录，以它的关键字作为“枢轴”，凡其关键字小于枢轴的记录均移动至该记录之前，反之，凡关键字大于枢轴的记录均移动至该记录之后，将序列划分：（小）枢轴（大）

2.2快排一趟后序列特征：存在一个元素，元素左边元素的关键字不大于它的关键字，它右边元素的关键字不小于它的关键字

2.3快速排序是不稳定的排序方法

2.4时间复杂度：最坏O(n^2);最好O(nlog2(n));平均O(nlog2(n))

2.5快速排序是所有同量级O(nlogn)的排序方法中，平均性能最好的方法

2.6快速排序的改进：进行一次划分之前，将左端与有右端与中间的关键字相比，拿三者的中间值做枢轴

四、选择排序

1.简单选择排序

1.1基本思想：

1.1.1第一次从n个关键字中选择一个最小值，从而确定第一个元素

1.1.2第二次再从剩余元素中选择一个最小值，确定第二个元素

1.1.3共需n-1次选择

1.2每次简单选择排序后将有一个最小元素排到最前面

1.3关键字间的比较次数总计为n(n-1)/2

1.4移动记录的次数：最小值为0，最大值为3(n-1)

1.5简单选择排序方法是不稳定的

1.6时间复杂度：比较O(n^2)，移动最好O(1)，最差O(n)

1.7空间复杂度：O(1)

2.树形选择排序

2.1又称锦标赛排序，是一种按照锦标赛的思想进行选择排序的方法

2.2首先对n个记录的关键字进行两两比较，然后递归比较前一步查找的[n/2](上取整)个关键字，如此重复直至选出最值关键字

2.3整个过程可以用n结点的完全二叉树表示

2.4排序算法时间复杂度：O(nlog(n))

3.堆排序

3.1堆排序属于选择排序：出发点是利用选择排序已经发生过的比较，记住比较的结果，减少重复比较的次数

3.2堆的定义：n个元素的关键字序列R[1].key,R[2].key,...,R[n].key，当且仅当满足下述关系时，称之为堆。

3.2.1R[i].key≤R[2*i].key且R[i].key≤R[2*i+1].key：小根堆

3.2.2R[i].key≥R[2*i].key且R[i].key≥R[2*i+1].key：大根堆（根结点的关键字最大）

3.3堆排序思想：

3.3.1由一个无序序列建成一个堆

3.3.2在输出堆顶元素后，调整剩余元素成为一个新的堆

3.4算法概要（大根堆）：

3.4.1按关键字建立大根堆

3.4.2输出堆顶元素，采用堆顶元素与最后一个元素交换，最大元素得到正确位置

3.4.3对此时的前n-1个元素重新建堆

3.4.4循环执行2.4.2与2.4.3，知到排序完成

3.5建堆算法：

3.5.1先根据下标建立完全二叉树

3.5.2从最后一个非叶子结点开始建堆（n个结点，最后一个非叶子结点的下标为[n/2]，将其与子结点比大小，不符合大小时，先横比，再纵比确定被取代结点的插入位置，逐渐向上一个非叶子结点转移比较[n/2]--->[(n-1)/2]--->......）

3.6堆排序是不稳定的排序

3.7时间复杂度为O(nlog(n))；最坏情况：O(nlog2(n))

3.8空间复杂度为O(1)

五、归并排序

1.归并的定义

1.1归并又叫合并，是指把两个或两个以上的有序序列合并成一个有序序列

1.2（根据比较循环的循环条件判断循环最多循环m+n-1次i<=m&&j<=n）将两个长度分别为n、m的递增有序序列归并为一个有序顺序表，元素最多的比较次数为m+n-1

2.（2路）归并排序思想

2.1将顺序表分n份分别进行递归排序（循环分割直到最后每个表仅剩一个元素）

2.2将n个记录进行2路归并排序的时间复杂度为O(nlog2(n))

2.3每一趟归并的时间复杂度为O(n)，总共需进行[log2(n)]上取整

2.4归并排序是稳定的排序方法

2.5空间复杂度为O(n)

3.K-路归并

3.1K路归并排序共需要logk(n)趟

3.2K路归并的时间复杂度为nlogk(n)

六、基数排序

1.基数排序的起源

1.1基数排序起源于箱（桶）排序，设置若干个箱子，依次扫描待排序的记录,A[1],A[2],...,A[n],把关键字为k的记录放在第k个箱子里,按序号将非空的箱子里的记录收集起来

1.2箱排序的缺点：如果关键字位数太大，这样做空间复杂度和时间复杂度都太大

2.链式基数排序

2.1待排序记录以指针相链，构成一个链表

2.2“分配”时，按当前“关键字位”所取值，将记录分配到不同的“链队列”中，每个队列中记录的“关键字位”相同

2.3“收集”时，按当前关键字位取值从小到大将各队列首尾相链成一个链表

2.4对每个关键字位均重复2.2 和2.3 两步

2.5基数排序需要的分配与收集次数为最大关键字的位数

2.6排序概要：（先根据个位分开收集，位数逐渐上升，没有实质性的元素间的比较最终却可以排序完成）

2.6.1设待排记录A的关键字最大是figure位的正整数

2.6.2从最低位(个位)开始，扫描关键字的pass位,把等于0的插入Q[0],...,等于9的插入Q[9]

2.6.3将Q[0]~Q[9]中的数据依次收集到A[]中

2.6.4pass+1直到figure，重复执行1，2两步

3.算法分析

3.1基数排序是稳定的

3.2空间复杂度与时间复杂度均为O(n)

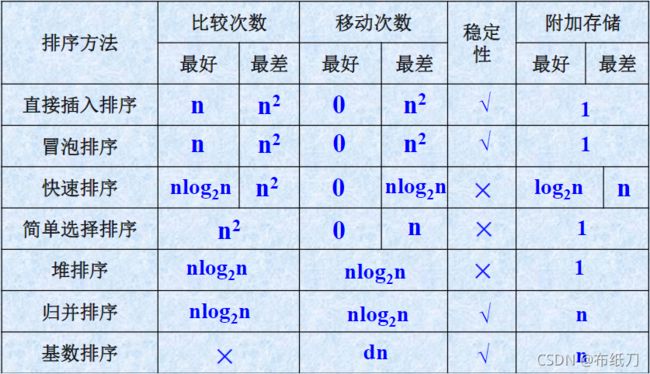
七、内部排序方法的比较

---

本笔记除了自己的一些理解外，参考《数据结构》，图片出自网络与课程ppt，如有侵权，请联系笔者删除。

最后希望大家一起学习，共同进步，如果有疑问或错误欢迎联系笔者。