电力系统潮流(Matlab实现)
关注:电力系统系列(Python&Matlab),更多干货等你拿.........
目录
1 概述
2 主要任务
3 主要内容
4 案例分析
5 PowerWorld仿真
5.1 正常工作
5.2 负荷增加
5.3 发电机出力增加
6 MATLAB编程实例
6.1 潮流计算程序流程图
6.2 潮流计算代码
1 概述
最初,电力系统潮流计算是通过人工手算的。后来为了适应电力系统日益发展的需要,计算机网络已经形成,为了电力系统的潮流计算提供了物质基础。电力系统潮流计算是电力系统分析计算中最基本的内容,也是的电力系统运行及设计中必不可少的工具。根据系统给定的运行条件、网络接线及元件参数,通过潮流计算可以确定各母线电压的幅值及相角、各元件中流过的功率、整个系统的功率损耗等。
本文通过介绍基于牛顿拉夫逊法和高斯赛德尔法的潮流计算,在MATLAB中对牛顿拉夫逊法的算法进行了验证,并且用PowerWorld搭建了简单的电力系统模型,对MATLAB结果加以验证,更加形象地了解实际电力系统中潮流的分布情况。
2 主要任务
(1)在电气工程领域,潮流计算、短路计算、稳定计算俗称电力系统的三大计算。
(2)高压输电网潮流的计算机算法程序设计(PQ分解法、牛顿-拉夫逊法)
(3)或中压配电网潮流的计算机算法程序设计(前推后代法、同伦延拓法等)
(4)或电力系统短路故障的计算机算法程序设计(要求不限)
3 主要内容
(1)根据电力系统网络推导电力网络数学模型,写出节点导纳矩阵;
(2)赋予各节点电压变量(直角坐标系形式)初值后,求解不平衡量;
(3)形成雅可比矩阵;
(4)求解修正量后,重新修改初值,从2开始重新循环计算;
(5)求解的电压变量达到所要求的精度时,再计算各支路功率分布、功率损耗和平衡节点功率;
(6)上机编程调试;连调;
(7)计算分析给定系统潮流分析并与手工计算结果作比较分析。
4 案例分析
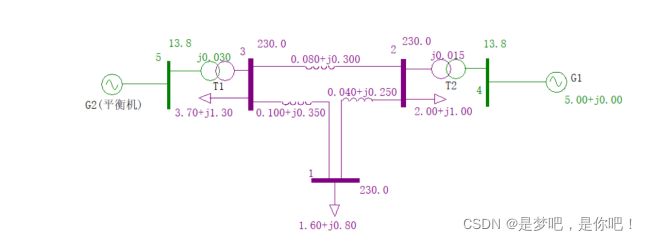
如图2-1所示,该系统由两台发电机、两台变压器、三条交流输电线路以及三个负荷组成的一个具有5节点的环网,其中节点1、2、3均为PQ节点,节点4为PV节点,节点5为平衡节点。图中参数均用标幺值表示,母线1、2、3基准电压为230kV,母线4、5基准电压为13.8kV,基准功率为100MVA。
5 PowerWorld仿真
5.1 正常工作
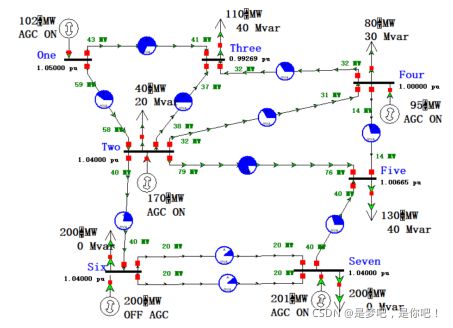
搭建一个基于PowerWorldd的复杂模型,如图所示,同时也表征着其正常运行状态下的潮流分布情况。
5.2 负荷增加
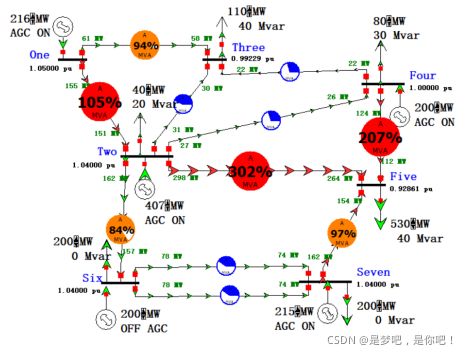
当节点Five上的负荷增加至530MW时,系统的潮流发生较大改变,如图所示,多条线路处于过负荷运行状态下,电压水平也降低了很多,说明在过负荷下会严重影响系统的电压水平。
5.3 发电机出力增加
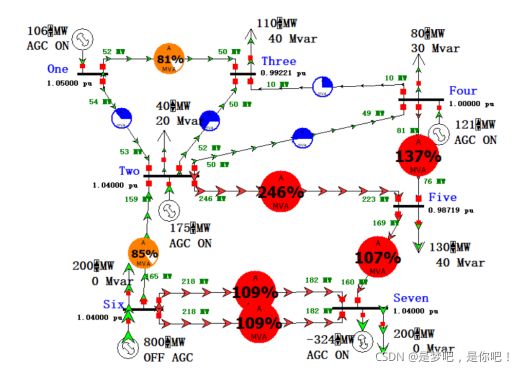
当节点Six上的发电机有功出力增加至800MW时,系统的潮流发生较大改变,如图所示,多条线路处于过负荷运行状态下,电压水平也稍有降低。
6 MATLAB编程实例
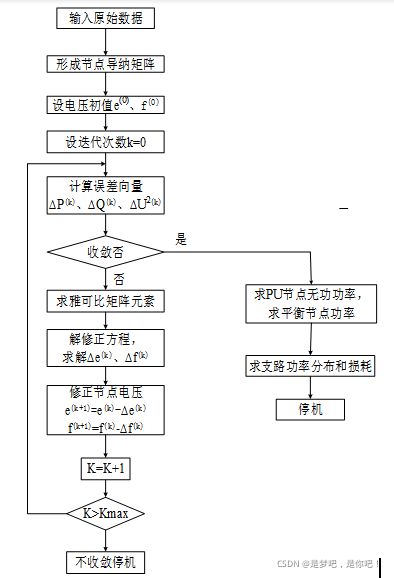
6.1 潮流计算程序流程图
基于牛顿-拉夫逊法的潮流计算程序流程图如图所示。
6.2 潮流计算代码
function [node_result,s_result] = PowerSystem % 潮流计算主程序
%%
[node] = OpenNode;
[nn,mn] = size(node); % 打开数据文件.并返回node
%%
[line] = OpenLine;
[nl,ml] = size(line); % 打开数据文件.并返回line
%%
[node,line,nPQ,nPV,nodenum,PH,PV,PQ] = Num(node,line); % 对节点重新排序
%%
Y = sparse(Yij(node,line)) % 计算节点导纳矩阵
%%
[U] = abs(Gauss_Seidel(Y,node,nPQ,nPV)) % 返回GS算法的结果,作为初值
%%
[node_result,s_result] =Newton_Raphson(U,Y,node,nPQ,nPV,line,nodenum); % 用牛顿拉夫逊法计算潮流结果
%%
Result_Write(node_result,s_result,node,line); % 把结果写入文件
function [node] = OpenNode
[dfile,pathname]=uigetfile('*.m','Select Node File'); % 数据文件类型为m文件,窗口标题为“Select Node File”
if pathname == 0
error(' you must select a valid data file') % 如果没有选择有效文件,则出现错误提示
else
lfile =length(dfile); % 去除文件后缀
eval(dfile(1:lfile-2)); % 打开文件
end
node = ...
[
1 1.00 0.00 -1.60 -0.80 1 ;
2 1.00 0.00 -2.00 -1.00 1 ;
3 1.00 0.00 -3.70 -1.30 1 ;
4 1.05 0.00 5.00 0.00 2 ;
5 1.05 0.00 0.00 0.00 3 ];
function [line] = OpenLine
[dfile,pathname]=uigetfile('*.m','Select Line File'); % 数据文件类型为m文件,窗口标题为“Select Line File”
if pathname == 0
error(' you must select a valid data file') % 如果没有选择有效文件,则出现错误提示
else
lfile =length(dfile); % 去除文件后缀
eval(dfile(1:lfile-2)); % 打开文件
end
line = ...
[
1 2 0.04 0.25 0.0 0.25 0 ;
1 3 0.10 0.35 0.0 0.0 0 ;
2 3 0.08 0.30 0.0 0.25 0 ;
5 3 0.00 0.03 0.0 0.0 1.05 ;
4 2 0.00 0.015 0.0 0.0 1.05 ];
function [node,line,nPQ,nPV,nodenum,PH,PV,PQ] = Num(node,line)
%%
[nn,mn]=size(node); % 获取nb和nl
[nl,ml]=size(line);
%%
nPH = 0; % nPH为平衡节点个数
nPV = 0; % nPV为PV节点个数
nPQ = 0; % nPQ为PQ节点个数
%%
for i = 1:nn, % nb为总节点数
type= node(i,6); % 判断节点类型
if type == 3,
nPH = nPH + 1; % 记录个数
PH(nPH,:)=node(i,:); % 矩阵PH计算并储存平衡节点
elseif type == 2,
nPV = nPV +1;
PV(nPV,:)=node(i,:); % 矩阵PV计算并储存PV节点
else
nPQ = nPQ + 1;
PQ(nPQ,:)=node(i,:); % 矩阵PQ计算并储存PQ节点
end
end
%%
node=[PQ;PV;PH]; % 对node矩阵按PQ、PV、平衡节点的顺序重新排序
%%
for i=1:nl
for j=1:2
for k=1:nn
if line(i,j)==nodenum(k,2)
line(i,j)=nodenum(k,1);
break
end
end
end
end % 按排序以后的节点顺序对line矩阵重新编号
function Y = Yij(node,line)
%%
[nn,mn]=size(node);
[nl,ml]=size(line);
%%
Y=zeros(nn,nn); % 对导纳矩阵赋初值0
%%
for k=1:nl
I=line(k,1);
J=line(k,2);
Zt=line(k,3)+j*line(k,4); % 读入线路参数
if Zt~=0
Yt=1/Zt; % 接地支路不计算Yt
end
Ym=line(k,5)+j*1/2*line(k,6); % 计算G+B
K=line(k,7); % 取变压器线路变比
%%
if (K==0)&(J~=0) % 普通线路: K=0
Y(I,I)=Y(I,I)+Yt+Ym; % YII为自导纳
Y(J,J)=Y(J,J)+Yt+Ym;
Y(I,J)=Y(I,J)-Yt; % 互导纳
Y(J,I)=Y(I,J);
end %求解导纳
%%
if (K==0)&(J==0) % 对地支路: K=0,J=0,R=X=0
Y(I,I)=Y(I,I)+Ym; % 直接加到自导纳上
end
%%
if K>0 % 变压器线路:折算到i侧,K在j侧,参考书上P108
Y(I,I)=Y(I,I)+Yt+Ym;
Y(J,J)=Y(J,J)+Yt/K/K;
Y(I,J)=Y(I,J)-Yt/K;
Y(J,I)=Y(I,J);
end
%%
if K<0 % 变压器线路:折算到j侧,K在i侧
Y(I,I)=Y(I,I)+Yt+Ym;
Y(J,J)=Y(J,J)+K*K*Yt;
Y(I,J)=Y(I,J)+K*Yt;
Y(J,I)=Y(I,J);
end
end
function YtYm = YtYm_NR(line) % 计算线路的等效Yt和Ym
[nl,ml]=size(line);
%%
YtYm = zeros(nl,5); % 对YtYm矩阵赋初值0,和线路行数相同,共5列
YtYm(:,1:2) = line(:,1:2); % 矩阵前两列为节点编号,后三列分别为线路等效Yt,i侧的等效Ym,j侧的等效Ym
j = sqrt(-1); % 用来代表i
%%
for k=1:nl
I=line(k,1);
J=line(k,2);
Zt=line(k,3)+j*line(k,4); % 读入线路参数
if Zt~=0
Yt=1/Zt; % 接地支路不计算Yt
end
Ym=line(k,5)+j*line(k,6); % 计算G+B
K=line(k,7); % 取变压器线路变比
%%
if (K==0)&(J~=0) % 普通线路: K=0
YtYm(k,3) = Yt;
YtYm(k,4) = Ym;
YtYm(k,5) = Ym;
end
%%
if (K==0)&(J==0) % 对地支路: K=0,J=0,R=X=0
YtYm(k,4) = Ym;
end
%%
if K>0 % 变压器线路: 参数折算到i侧,K在j侧,参考书上P108
YtYm(k,3) = Yt/K;
YtYm(k,4) = Ym+Yt*(K-1)/K;
YtYm(k,5) = Yt*(1-K)/K/K;
end
%%
if K<0 % 变压器线路: 参数折算到j侧,K在i侧
YtYm(k,3) = -Yt*K;
YtYm(k,4) = Ym+Yt*(1+K);
YtYm(k,5) = Yt*(K^2+K);
end
end
%%
while k % k不为0就继续计算
for i=1:nn
switch node(i,6) % 判断节点类型
case 1 % 1为PQ节点
[U1] = PQ(i,U,node,Y,nPQ); % 代入PQ子程序中
U(i,1)=U1(i,1); % 把值放到U矩阵中
case 2 % 2为PV节点
[U2] = PV(i,U,node,Y,nPV); % 代入PV子程序中
U(i,1)=U2(i,1);
case 3 % 3为平衡节点,不变
U(i,1)=node(i,2)*cos(node(i,3))-node(i,2)*sin(node(i,3))*sqrt(-1);
end
end
k=k-1;
end
function [node_result,s_result] =Newton_Raphson(U,Y,node,nPQ,nPV,line,nodenum)
% 牛顿拉夫逊法主程序
[nn,mn] = size(node);
%%
EPS = 1.0e-10; % 设定误差精度
%%
for t = 1:1000 % 开始迭代,最大迭代次数为1000,不收敛时跳出
%%
[dP,dQ] = DPQ(Y,node,nPQ,nPV); % 计算P与Q的偏差
%%
Jac = Jac_NR(node,Y,nPQ);
%Jac = sparse(Jac_NR(node,Y,nPQ)); % 计算雅克比矩阵
%%
UD = zeros(nPQ,nPQ);
for i = 1:nPQ
UD(i,i) = U(i,1); % 生成电压对角矩阵,方便计算,在书上P117
end
%%
dAngU = Jac \ [dP;dQ]; % 公式在P117
dAng = dAngU(1:nn-1,1); % 计算相角修正量
dU = UD*(dAngU(nn:nn+nPQ-1,1)); % 计算电压修正量
node(1:nPQ,2) = node(1:nPQ,2) - dU; % 修正电压
node(1:nn-1,3) = node(1:nn-1,3) - dAng; % 修正相角
%%
if (max(abs(dU))完整代码点这里:潮流仿真(Matlab and PowerWord)