【基础篇】理解区块链的结构及其设计原理
国内目前已经有众多关于区块链、比特币等的新闻和文章,但大多只是粗浅的讲述了“区块链是去中心化的分布式账本”等概念,且在去中心化、加密货币等方面大做文章。
对比国外在区块链技术原理、技术改进和内在逻辑等的讨论,国内的新闻媒体、大佬和所谓的三点钟区块链群等,还多集中在绿皮火车化的讨论,一些深层次的讨论文章实在是少之又少。
我每每在回顾并感慨区块链近几年的快速发展时,总是在思考:如果我是中本聪的话,当初为何会想到要提出区块链的概念?我为何会引入哈希(Hash)函数、创造比特币呢?又为何会想到用PoW的共识模型和方法?最后,怎么把上述几个概念结合成一起,形成区块链的逻辑?
以下的正文均是依据上述的逻辑展开的。
需要提醒的是,以下的正文需要对经济、数学有一定的了解和兴趣,对于区块链这样一个复杂又有意思的新事物而言,仅用活泼的语言和简单的例子来解释,尽管对于普通读者可以达到简单易懂的作用,但是要想真正的理解区块链的原理和实现的机制,不了解背后的理论,绝对是远远不够的。
下面进入正文。
一、中心化的系统
对于一个电子现金交易系统(Electronic Cash System)而言,常见的交易情景如下:
A现在要去购买一台电脑,并支付1万元给商户B。
1. A的账户里有1.5万元;
2. A将自己账户里的1万元通过网络发送给B;
3. B确认A发送的这笔“电子现金(Electronic Cash)”真实无误后,将电脑给A;
4. 最后,A账户里只剩下5千元,B账户里增加了1万元。
如果是线下交易,A和B之间“一手交钱、一手交货”,B能轻而易举的验证这笔钱的真实性,然而对于上述的电子现金交易,最明显的一个问题为:(1)B无法确认A这笔电子现金是否是真的,即A的账户里是否有足够的1万元来支付;(2)A账户里支付给B的1万元之前是否已经支付给了其他人C,即“双重支付(Double-Spending)”的问题。
通常,为了解决这个问题,现实中往往引入一个值得信任的第三方(往往是政府、银行等机构),来担当中间人的身份。此时的交易情景如下:
1. A向银行账户里存入1.5万元现金,银行会在A的电子账户中增加/“发行”1.5万元的Electronic Cash;
2. A将自己账户里的1万元Electronic Cash通知银行发送给B;
3. 银行确认A发送的这笔Electronic Cash真实无误,支付给B;
4. B确认收款,并将将电脑给A;
5. A账户里只剩下5千元Electronic Cash,B账户里增加了1万元Electronic Cash;
6. 如果A账户里不足1万元Electronic Cash,则银行会提示A付款失败;如果A之前已经把这1万元支付给了C,则银行会提示A存款不足。
可见,作为第三方的银行解决了交易验证及Double-Spending等问题。
那么问题来了:
- Q1:如何在没有第三方机构的情况下,解决上述问题呢?更进一步说,是否存在一个去中心化的系统,在没有银行的帮助下,使得交易双方可以进行直接的点对点货币交易?
二、银行的总账和区块链的总账
银行的做法能为我们提供一个基本的思路。通过学习银行的做法,了解银行解决上述问题的根本原因,从而设计出一套既能去中心化、又能解决上述问题的系统。那么银行是通过怎样的办法,解决上述问题的呢?
一般而言,银行自己对每一笔交易都有一本“总账”,在这笔总账上,记录着每一个人的交易记录(收入+支出)、余额、时间等基本信息。每“确认”一笔收入,则加盖相应“时间戳”,对这笔交易做“+”处理;每“确认”一笔支出,则加盖相应的“时间戳”,对这笔交易做“-”处理。因此,每一个人的账户余额,是按照时间顺序进行加减得到的最终结果。
在前述提到的A和B之间的交易情景中,当A需要向B支付1万元的Electronic Cash时,银行把A的账本从“总账”里拿出来进行对比,如果A账本中在考虑了所有已“确认”的交易后,账户余额足以支付1万元,则认为交易无误且支付给B,B银行在收到Electronic
Cash后通知B到账成功,B则可放心交货给A。
银行的做法有几个重要逻辑:
1. 有一笔总账,记录着每一个人的账本,以供查询并对账;
2. 这笔总账只有银行有权利记账(银行是有公信力的机构);
3. 每一个人的账本都详细记录着每一笔交易、相应的时间戳、余额等信息;
4. 只有当一笔交易被“确认”后,才会作为收入/支出记录在账本中。
参考上述银行的做法便可得知:若要解决问题一“去中心化”,核心是有一个“总账本”并满足以下条件:
(1)公开透明的(中心化的情况下,因为银行保证了你账本的真实性,所以无需公开透明;但没有银行时,只有允许账本公开透明,才能使得卖家知道买家账上是否有足够的钱来支付款项;)
(2)可供所有人查询并对账的(中心化的情况下,银行保证了你账本是真实的;但没有银行时,只有允许其他人都可以查询且对账,才能确保买家账本的真实性,否则买家可能虚报自己的账本)
(3)记账权力是公平且安全的(记账权利是指谁可以有权利修改账本,中心化的情况下,银行只有在你存款了后才会在你的账本上记账,只有银行才有记账权利,但在没有银行时,谁有权利记账呢?必须保证修改账本的权利是公平且安全的,否则任何人都可以随意篡改自己的账本,例如自己给自己账本上+1亿元)
(4)记录了所有人已确认交易记录的(已确认交易是为了避免“双重交易”,如果某笔交易没有被确认却被记账了,会导致账本余额数量对不上。例如A账本有1.5万元,需要给B支付1万元,指令已发出但后面交易取消,如果此时依然记账,A账本就只有0.5万元,是错误的。中心化的情况下,取消交易后银行会调整账本,但没有银行时,谁有权利调整呢?)
试想,如果现实生活中有一个满足上述四个条件的“总账本”,此时,A和B的交易情景将会如下:
1. A的电子账户中有1.5万元Electronic Cash,该信息记录在“总账本”中,可供所有人查询;
2. A购买电脑,并将自己账户里的1万元Electronic Cash通知网络发送给B;
3. B查询该“总账本”,验证得知A的这笔钱没有问题,并确认收款;
4. A账户里只剩下5千元Electronic Cash,B账户里增加了1万元Electronic Cash;
5. 如果A账户里不足1万元Electronic Cash,B验证得知后将拒绝A提货;如果A之前已经把这1万元支付给了C,B同样也会验证得知并拒绝A。
可见,如果真的存在上述这样一个账本,那么第三方公信力的机构似乎没有了存在的价值,我们便解决了Q1的疑问:的确存在一个去中心化的Electronic Cash System,使得交易双方可以进行直接的点对点货币交易。
三、哈希函数和公开总账本的安全性
但要实现上述逻辑并不简单,上面的分析表明,我们遇到的进一步的问题是:
- Q2:谁有权利记账?
- Q3:如果有记账人,如何保证该记账人不会为了自己的利益修改记录(即如何保证记账人有银行一样的公信力)?
- Q4:如何保证账本不被篡改,例如修改以前的历史记录(即如何保证账本的安全性)?
- Q5:谁有权力对交易进行确认和验证(即证明各笔交易是否真实有效)?
我们一个一个问题来看。首先,谁有权利记账?既然我们要设计的系统是去中心化的,显然我们不能把记账的权力交给某一个第三方,而把记账的权利交给某一个人显然也是不放心的,在考虑到公平公正的前提下,一个容易的推导是:
所有人都可以记账,任意一笔记账都需要绝大多数人进行确认和验证,且只有在绝大多数人同意的前提下才能被认为是真实有效的(即达成一致consensus)。
这个方法的公平性是显而易见的。所有人都可以记账,但是需要经过绝大多数人的同意,也需要绝大多数人的确认和验证。如果大家不同意,则这笔交易就不被确认,不被记到账本上;如果大家同意,则确认并记录。
我们可暂且将技术原理放在一边,如果这是能做到的,那么问题Q2,Q3,和Q5也就解决了。一是所有人都有记账权利,则解决了Q2。二是因为记账需要大多数人同意,所以不会存在记账人为了自己利益修改记录的行为,因为这样的行为会被大家否认,则解决了Q3;最后每一笔交易都确保了真实有效,因为每一笔交易都需要大家的确认和验证,则解决了Q5。
在这个前提下,我们又该如何解决问题Q4,即如何保证历史记录不被篡改呢?
保证历史记录不被篡改,有几个容易想到的思路:
第一种思路是,我们可以给历史记录加上一把复杂的”密码锁“,任何人要修改账本的历史记录需要解开这把锁。这个思路的前提是,这把锁不会妨碍人们对历史记录的查询和验证,且不会妨碍人们添加新的交易记录(即新的记账)。可是,这把锁的钥匙、密码归谁保管呢?
第二种思路是,但凡有人对历史记录的进行了修改,哪怕只是一丁点儿修改,都会引起一个较大的变化,以至于被人们发现且拒绝。
第三种思路是,对历史记录的修改的需要花费的成本巨大,且随着时间的推移越来越大,大到普通的人无法承受。这个思路的缺陷在于,你永远都不知道富人究竟有多富。
若要理解接下来的内容,可能需要一些数学思维。
数学家们对这个世界做出了无比重大的贡献,他们发明的“哈希函数”将在这个系统中发挥巨大的作用。先简单介绍一下哈希函数:
哈希函数,一般也叫做散列函数,是把任意长度的输入变换成固定长度的输出,该输出被称为散列值。简单地说,就是一种将任意长度的消息压缩成某一固定长度的信息摘要的函数。举个熟悉的例子,就像是以前的语文阅读题目,请用10个字概括这篇需要阅读的文章,在这里10个字就是固定长度的输出,数学上称为散列值;这篇需要阅读的文章是任意长度的输入。把这篇任意长度的文章变换成固定10个字的散列值,我们称之散列函数,或者哈希函数。
数学上,一个良好性质的哈希函数(HASH函数,通常用h(x)来表示)必须具备以下特征:
1. 任何大小的数据分组,h(x)函数都能产生固定长度的输出
2. 对于任何给定的自变量key,哈希值h(key)要相对容易计算
3. 单向性:指的是其操作方向的不可逆性,即只能从输入推导出输出,而不能从输出计算出输入。即:已知自变量key1,可以计算出h(key1)=h1;但已知因变量h1,若想推导出对应的自变量key1,在计算上不可行(“计算上不可行”的定义见下)。
4. 碰撞约束。碰撞约束可分为弱抗碰撞和强抗碰撞。所谓弱抗碰撞,指的是对于给定的自变量key1,若想找一个与key1不一样的另一个自变量key2,使得h(key1)=h(key2),在计算上不可行;所谓强抗碰撞,指的是寻找任何的自变量(key1, key2)使得h(key1)=h(key2),在计算上不可行。
上述提到的“在计算上不可行(Computationally Infeasible)”,意思并不是“完全不可能”,而是“很难很难“,或者说”要在有限的时间内计算出来不可能“。
小知识(可忽略):
目前常用的HASH函数主要有两个系列,MD和 SHA系列。其中,MD系列主要包括 MD2,MD4,MD5,但这类HASH函数已经被证实不够安全(我国山东大学教授王小云在有限的时间内成功地破解了MD2和MD5算法)。SHA系列主要包含SHA1和 SHA2(SHA224, SAH256, SHA384,SHA512)系列,其中224,256,384,512都是指其输出的位长度。目前大多数应用场景推荐使用SHA256以上的算法。目前以超级计算机的算力,产生比特币SHA256哈希算法的一个哈希碰撞大约需要2^48年。
假设某一笔交易的历史记录我们设为自变量key1,哈希函数的上述性质告诉我们,很难找到一个不等于key1的另一笔交易记录key2,使得h(key1)=h(key2)。这也意味着:
(1)对于key1的任何变动,哪怕是一点点,都将使得哈希值/输出值与原输出值h(key1)完全不相等或者差异巨大;这就是说交易记录的一点点改变,哈希值的变化都会足以引起人们的注意。
(2)如果后一个哈希函数的输入是基于前一个哈希函数的输出,那么,如果要修改任何一个时点的历史记录,就要把前面所有时点的历史记录及其对应的哈希值都进行修改,并找到相应的哈希碰撞,而哈希函数的性质告诉我们,这在计算上是相当难实现的。换句话说,如果哈希函数的自变量不是交易记录key1,而是交易记录的哈希函数h(key1),即自变量x1 = h(key1), 因变量y = h(x) = h[h(key1)]。此时,如果某人尝试把交易记录key1改变成key2,但又不想让别人发现,那么y = h[h(key1)] 就需要不变。也就是要使得y = h[h(key1)] = h[h(key2)]。而根据前面哈希函数的性质4“碰撞约束”:若想找一个与x1不一样的另一个自变量x2,使得h(x1)=h(x2),在计算上不可行。
基于以上,我们很容易想到,这个性质如果能应用到我们前面提到的思路,那将是非常完美的。如果能把某一时点的交易记录进行哈希,且该哈希的输出是以后时点的交易记录哈希的输入,即h(x2) = h(h(x1)),那么不同时间点的交易记录之间将通过哈希进行紧密联系,任何一处的变动不仅将改变其自身的哈希,还会改变以他为参数之一的后面交易记录的所有哈希,而且根据哈希函数的性质,如果要找到另一个数使得后面的哈希不变,这在计算上是不可行的。也就是说,对历史记录的任何一点修改将随着时间的推移越来越难、成本越来越高,且在计算上无法篡改。
四、推理出区块链结构
因此,我们可以推导出区块链结构的初步框架:
1. 新加入了交易记录后,新账本记作Bn,则Bn需要至少包含以下内容:
(1)Bn对应发生的时间,即“时间戳”,记为tn
(2)包含的所有交易记录,记为TXn
(3)上一个账本的哈希值,记为B(n-1)。
所以:Bn=H(tn, TXn, B(n-1)),
其中H(x)是哈希函数,是对自变量x进行哈希。所以Bn是对三个自变量tn, TXn, 以及B(n-1)一起进行哈希的结果。
2. 由于一个账本中可以包含很多的交易记录,为了让这么多交易记录变成一个自变量,从而简化交易记录在哈希函数中的输入,我们可以对交易记录进行哈希,也就是把很多的交易记录TX1,TX2, TX3......进行哈希,变成一个输入值。
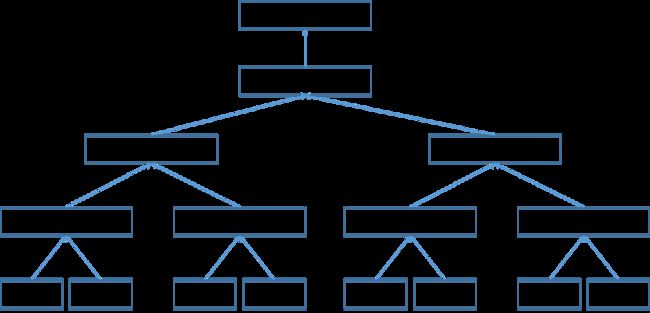
一个巧妙的方法是以“默克尔树(Merkle Tree)”来验证并记录交易。Merkle Tree也称为Hash Tree,本质是存储哈希值的二叉树。从下图可看出,Merkle Tree的每个叶子节点是每个交易信息的哈希值,往上对相邻的两个哈希值再哈希,一直到顶部只剩下一个节点,称为Merkle根。将数据以Merkle树的方式存储的好处是,可以单独拿其中的一个小分支对部分数据进行验证,而无需对所有数据都进行审阅,提高效率。
由此可见,通过上述方法,我们把一个账本中包含的众多交易,通过不断的哈希,最后变成了一个变量,即Merkle根。我们只需要用Merkle根作为账本的一个变量,即可包含所有交易记录。
即:Bn=H(tn, Merkle-n, B(n-1)),
其中,Merlke-n=H(TXn),所以Bn是对三个自变量tn, Merlke-n, 以及B(n-1)一起进行哈希的结果。
到这里,我们可以暂时回顾一下目前的进展。我们之前提出了5个问题:
- Q1:如何在没有第三方机构的情况下,解决上述问题呢?更进一步说,是否存在一个去中心化的系统,在没有银行的帮助下,使得交易双方可以进行直接的点对点货币交易?
--> 通过借鉴银行的做法,我们提出,若要解决去中心化的问题,核心是有一个公开透明的、可供所有人查询并对账的、记账权利是公平且安全的、记录了所有人已确认交易记录的“总账本”。
- Q2:谁有权利记账?
- Q3:如果有记账人,如何保证该记账人不会为了自己的利益修改记录(即如何保证记账人有银行一样的公信力)?
- Q5:谁有权力对交易进行确认和验证(即证明各笔交易是否真实有效)?
--> 在去中心化的情况下,我们提出需要所有人都可以记账,任意一笔记账都需要绝大多数人进行确认和验证,且只有在绝大多数人同意的前提下才能被认为是真实有效的(即达成一致consensus)。
- Q4:如何保证账本不被篡改,例如修改以前的历史记录(即如何保证账本的安全性)?
--> 利用哈希函数的性质,包含了新的交易记录的账本Bn=H(tn, Merkle-n, B(n-1)),新账本Bn和旧账本B(n-1)通过哈希函数紧密联系,对历史记录进行哪怕一丁点的修改,都会引起新账本Bn的值发生巨大变化,且随着时间的推移,要对账本进行篡改需要花费的成本越来越高,因此计算上可以认为账本不太可能被篡改。
3. 基于前面问题的讨论,我们已经决定不能将记账的权力交给某个单一的第三方,二是所有人都可以记账。但是,即使是所有人都有权利记账,我们依然要解决每一笔账具体由谁来记的问题,否则如果大家都只是有权利、而没有义务去记账,最后的结果就是谁都不记账,陷入“三个和尚没水喝”的困境。
比特币区块链的做法是引入了一个“竞争机制”。通过在前述的函数Bn=H(tn, Merkle-n, B(n-1))中,引入一个随机数nounce,即Bn=H(tn, Merkle-n, B(n-1), nounce),让所有人“公平”地去寻找这个随机数,使得Bn小于“目标哈希值”(以后会解释,此处可暂时理解为一个常数,即找到这个随机数,使得函数值Bn小于某个数)。谁先找到这个随机数,谁就获得了记账的权利。由于找到这个随机数在数学上的唯一方法只有通过穷举,因此谁的计算速度快、谁就先能找到这个随机数,获得记账的权利(因此,从某种意义来讲,这种记账权利并不是完全“公平”的,所以才会有诸如Proof of Stake等其他方法)。计算速度考验的是计算机的算力,而算力是耗费成本的,为了补偿使用算力造成的成本,这个账本会凭空产生出一个“代币”——虚拟货币“比特币”(Bitcoin)——发放给赢得记账权利的人,称为“旷工”,旷工通过消耗算力、找到随机数、赢得记账权利、并获得比特币被称之为“挖矿”,通过算力来进行挖矿的过程,被称为工作量证明(PoW,Proof of Work)。
基于此,我们进一步修改账本的哈希函数:
Bn=H(tn, Merkle-n, B(n-1), nounce),
其中,Merlke-n=H(TXn), nounce是随机数。旷工需要找到nounce,使得Bn<目标哈希。
五、画出区块链结构
基于前面的函数,我们知道一个新的区块/账本中,包含至少五个参数:时间戳tn,前一个区块的哈希值B(n-1),随机数nounce,目标哈希,以及Merkle根,这五个参数将包含在“区块头”中(当然还包括一些其他参数,例如版本号,相关性较小我们此处暂时忽略);此外,我们知道,Merkle根其实是包含所有交易记录的一个哈希值,因此每一个区块中还有一个“区块体”,记录着所有的交易记录。清楚的区块链结构如下:
简化的比特币区块链结构如下:
了解了区块链的理论后,接下来我们不妨看几个实际的区块的例子:
根据http://Blockchain.info提供的信息,我们随机找一个区块,例如第512352个区块,其详细信息如下图。从下图左侧提供的所有信息,由上到下可以看到:
- 该区块中包含1669笔交易(Number of Transactions: 1669)
- 区块包含的交易量有980.8783个比特币(Estimated Transaction Volume)
- 旷工得到的交易费未0.255548个比特币(Transaction Fees)
- 这是第512352个区块(Height)
- 时间戳(Timestamp)为2018年3月7日2点52分27秒
- 记账人未http://BTC.com(Replayed By BTC.com)
- 困难程度未3,290,605,988,755(以后会解释)
- 该区块大小为1099.549kB
- 版本号未0x20000000
- 随机数nounce为1152756558
- 旷工得到了12.5比特币的奖励
右侧由上到下提供的信息分别为:
- 该区块的哈希值(Hash)
- 上一个区块(也称为“父区块”)的哈希值(Previous Block)
- 下一个区块的目标哈希,即下一个区块的哈希值不得大于00000000000000000011d9deb41bfd546610de982fcbedfa251b52e2eec8719c
- 该区块所有交易记录的Merkle根。
至此,区块链的基础结构原理就完成了。
不过,若要深入的追问的话,我们会问:
- 一个新区块里包含的那些交易取决于谁?旷工可以自行决定吗?旷工可以决定什么交易都不放吗(即区块体中不包含任何交易记录)?
- 前面提到,新区块的哈希值要小于目标哈希,谁有权利决定目标哈希?
- 区块链的困难程度difficulty是什么?怎么计算的?难度值会调整吗?怎么调整?谁有权利调整?有什么意义?
- 旷工找到符合要求的随机数nounce后,即产生了一个新区块,这个新区块一定就会被加到主账本上去吗?如果不一定,要通过什么机制才能加入?
- 要是两个旷工同一时间找到了符合要求的随机数nounce,两个都符合要求的新区块被同时找到,怎么办?两个区块都加入新账本吗?还是只有一个可以加入?如果只有一个可以加入,谁来决定?
- 旷工获得比特币的奖励,比特币会被存放在哪里?不会被偷吗?存放的机制是怎样的?
- 比特币可以用来交易吗?比特币用于交易的机制,与现实社会中的货币交易机制有什么不同?
- 前面提到,通过算力来挖矿叫做PoW(Power of Work),那PoS(Power of Stake)是什么?孰优孰劣?
- 等等。。。。
这些问题会在专栏的其他文章中慢慢解释~~欢迎有兴趣的小伙伴一起讨论!