109. Magic of David Copperfield II 构造 难度:2
109. Magic of David Copperfield II
time limit per test: 0.25 sec.
memory limit per test: 4096 KB
The well-known magician David Copperfield loves lo show the following trick: a square with N rows and N columns of different pictures appears on a TV screen, Let us number all the pictures in the following order:
| 1 | 2 | ... | N |
| ... | ... | ... | ... |
| N*(N-1)+1 | N*(N-1)+2 | ... | N*N |
Each member of the audience is asked to put a finger on the upper left picture (i.e., picture number one) and The Magic begins: the magician tells the audience to move the finger K1 times through the pictures (each move is a shift of the finger to the adjacent picture up, down, left or right provided that there is a picture to move to), then with a slight movement of his hand he removes some of the pictures with an exclamation "You are not there!", and ... it is true - your finger is not pointing to any of the pictures removed. Then again, he tells the audience to make K2 moves, and so on. At the end he removes all the pictures but one and smiling triumphantly declares, "I've caught you" (applause).
Just now, David is trying to repeat this trick. Unfortunately, he had-a hard day before, and you know how hard to conjure with a headache. You have to write a program that will help David to make his trick.
Input
The input file contains a single integer number N (1<N<101).
Output
Your program should write the following lines with numbers to the output file:
K1 X1,1 X1,2 ... X1,m1
K2 X2,1 X2,2 ... X2,m2
...
Ke Xe,1 Xe,2 ... Xe,me
where Ki is a number of moves the audience should make on the i-th turn (N<=Ki<300). All Ki, should be different (i.e. Ki<>Kj when i<>j). Xi,1 Xi,2 ... Xi,mi are the numbers of the pictures David should remove after the audience will make Ki moves (the number of the pictures removed is arbitrary, but each picture should be listed only once, and at least one picture should be removed on each turn).
A description of the every next turn should begin with a new line. All numbers on each line should be separated by one or more spaces. After e iterations, all pictures except one should be removed.
Sample Input
3
Sample Output
3 1 3 7 9 5 2 4 6 8
一开始被题意吓住了,但是画一画就能发现,
只要是奇数步,就不能停留在原位,要是把整个迷宫划分成国际棋盘的黑白格,那么奇数步必然只能转移到异色格上,
注意到这点而且题目是special judge ,只需注意随时保持还没被染色的在一块大联通域里面就行了,(要是被孤立了那么玩家就不能再走,魔术师就算是没有完成魔术,要是多个区块就不知道玩家到底在哪个区块了,这样无法消除到只有一个含一块的区块)
这里为了保证这一点我使用的是从外向里,每次推一层的方法,假设出发点(0,0)是白格(计算中使用了二维坐标,结果转化为i*n+j+1)
对于里面的第i层,先消去上一层i-1层未涂色的白格,再消去i层可以消去的白格(相邻的黑格都有两个及以上个没有被消去的白格相邻),最后新建一个操作,消去i层的所有黑格(这时候i层的白格不会受影响,因为还有i+1层)
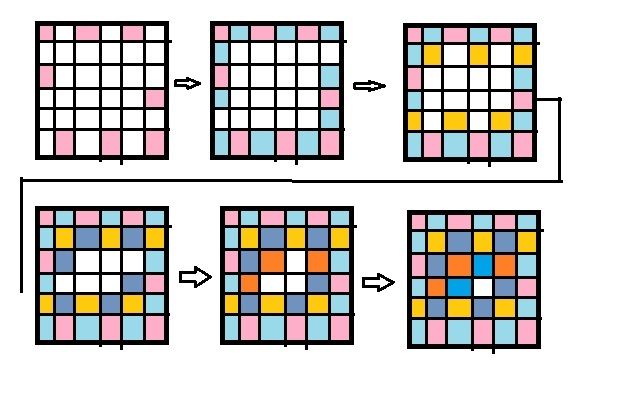
大致染色过程如图
因为染色操作最多有(n/2)*2,开头使用n也不会超出300的操作数
W原因:没有注意到ki<300
#include <cstdio>
#include <cstring>
using namespace std;
const int maxn=102;
const int dx[4]={1,0,-1,0},dy[4]={0,1,0,-1};
bool vis[maxn][maxn];
int n;
int heap1[maxn*maxn],len1,heap2[maxn*maxn],len2,heapt[maxn*maxn],lent;//heap1 第i圈可以消去的白 heap2 第i-1圈没有消掉的白 heapt 第i圈的第二个操作消去的黑格
bool oneentry(int x,int y){//只有一个出口
int fl=0;
for(int i=0;i<4;i++){
int tx=x+dx[i],ty=y+dy[i];
if(tx>=0&&tx<n&&ty>=0&&ty<n&&!vis[tx][ty]){
fl++;
}
}
return fl<=1;
}
bool avail(int x,int y){//是否会抓住顾客
for(int i=0;i<4;i++){
int tx=x+dx[i],ty=y+dy[i];
if(tx>=0&&tx<n&&ty>=0&&ty<n&&!vis[tx][ty]){
if(oneentry(tx,ty))return false;
}
}
return true;
}
int main(){
while(scanf("%d",&n)==1){
memset(vis,0,sizeof(vis));
len1=len2=lent=0;
int num=n&1?n:n+1;
for(int i=0;i<n/2;i++){
printf("%d ",num);num+=2;
for(int k=0;k<len2;k++)printf("%d ",heap2[k]);//上层未涂色白格
len1=len2=lent=0;
int x=i,y=i;
for(int dr=0;dr<4;dr++){
for(int j=0;j<n-2*i-1;j++){
if((x+y)&1){heapt[lent++]=x*n+y+1;vis[x][y]=true;}//黑格
else if(avail(x,y)){heap1[len1++]=x*n+y+1;vis[x][y]=true;}//暂时不能选的白格
else {heap2[len2++]=x*n+y+1;vis[x][y]=true;}//可选择白格
x+=dx[dr];
y+=dy[dr];
}
}
for(int k=0;k<len1;k++){
printf("%d%c",heap1[k],k==len1-1?'\n':' ');//涂白格
}
printf("%d ",num);num+=2;
for(int k=0;k<lent;k++)printf("%d%c",heapt[k],k==lent-1?'\n':' ');//涂黑格
}
}
return 0;
}