机器学习入门之逻辑回归(1)- 成绩预测是否进入大学(python实现)
一、基础知识
-
假设函数
对于logistic回归,假设函数是sigmoid函数,形式如下:
h θ ( x ) = 1 1 + e − θ T x (1) h_\theta(x) = \frac{1}{1+e^{-\theta^Tx}}\tag{1} hθ(x)=1+e−θTx1(1)
其中 θ T x \theta^Tx θTx是与线性回归的目标函数是一样的,这里的sigmoid函数是通过logistic分布得来的,logistic分布函数:
F ( x ) = P ( X ≤ x ) = 1 1 + e − ( x − μ ) γ (2) F(x) = P(X≤x) = \frac{1}{1+e^{-\frac{(x-\mu)}{\gamma}}}\tag{2} F(x)=P(X≤x)=1+e−γ(x−μ)1(2)
可得到密度函数:
f ( x ) = e − ( x − μ ) γ γ ( 1 + e − ( x − μ ) γ ) 2 (3) f(x)=\frac{e^{-\frac{(x-\mu)}{\gamma}}}{\gamma(1+e^{-\frac{(x-\mu)}{\gamma}})^2}\tag{3} f(x)=γ(1+e−γ(x−μ))2e−γ(x−μ)(3)
其中上式中的 μ \mu μ和 γ \gamma γ分别是位置参数和形状参数
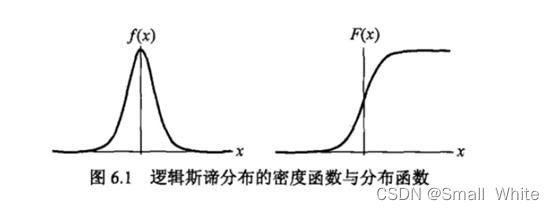
可以得到分布函数与概率密度的图像:
我们在分布函数,即函数(2)中的 μ \mu μ取值为0, γ \gamma γ取值为1,我们即可以得到sigmoid函数:
g ( z ) = 1 1 + e − z (4) g(z) = \frac{1}{1+e^{-z}}\tag{4} g(z)=1+e−z1(4)
其中
z = θ T x z = \theta^Tx z=θTx
这样就得到了(1)式,则我们可以sigmoid函数图像:
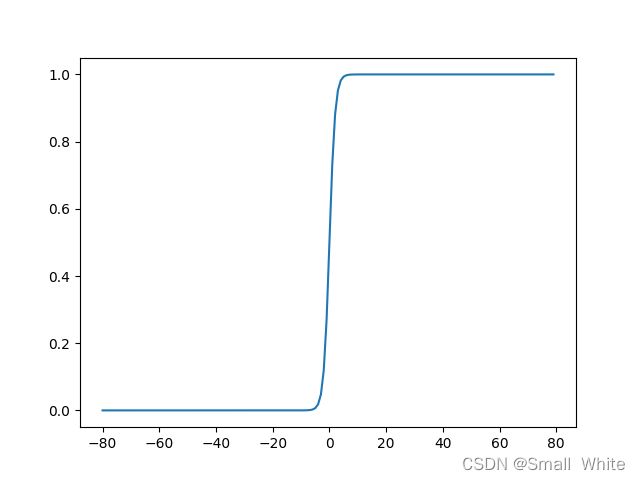
从(4)式和上面的图像中我们可以得知:
当 z → ∞ z\rightarrow\infty z→∞时, g ( z ) → 1 g(z)\rightarrow1 g(z)→1
当 z → − ∞ z\rightarrow-\infty z→−∞时, g ( z ) → 0 g(z)\rightarrow0 g(z)→0
当 z = 0 z=0 z=0时, g ( z ) = 0.5 g(z)=0.5 g(z)=0.5
这样我们可以假设设置阈值【当然阈值可以自己自由选择】,当 z > 0 z>0 z>0时,此时 g ( z ) > 0.5 g(z)>0.5 g(z)>0.5,则可以认为此时为1的概率值为100%,当 z ≤ 0 z≤0 z≤0时,此时 g ( z ) ≤ 0.5 g(z)≤0.5 g(z)≤0.5,则可以认为此时为0的概率值为100%
注意:对于输出的值我们可以认为是 p ( y = 1 ∣ x ; θ ) p(y=1|x;\theta) p(y=1∣x;θ)或 p ( y = 0 ∣ x ; θ ) p(y=0|x;\theta) p(y=0∣x;θ)的概率 -
损失函数
对于损失函数,不能使用预测值与真实值差的平方的均值来实现,对于(1)式的目标函数,平方后是非凸函数—(非凸函数是会有很多极小值,那么我们在梯度下降的时候是不容易找到最小值的),于是我们使用下列损失函数:
J ( θ ) = { − l n ( h θ ( x ) ) i f y = 1 − l n ( 1 − h θ ( x ) ) i f y = 0 (5) J(\theta) = \begin{cases} -ln(h_\theta(x)) & if \ y = 1\\ -ln(1-h_\theta(x)) & if \ y = 0 \end{cases}\tag{5} J(θ)={−ln(hθ(x))−ln(1−hθ(x))if y=1if y=0(5)
我们先分析 y = 1 y=1 y=1时的情况,为了方便理解,我们可以得到 − l n ( h θ ( x ) ) -ln(h_\theta(x)) −ln(hθ(x))的图像:
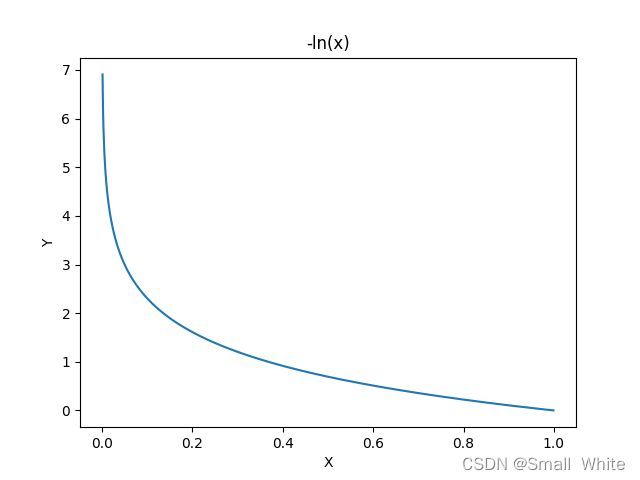
根据 y = 1 y=1 y=1时的 J ( θ ) J(\theta) J(θ)图像, y = 1 y=1 y=1时的损失函数这样理解:当 y = 1 y=1 y=1时,如果此时的 h θ ( x ) → 1 h_\theta(x)\rightarrow1 hθ(x)→1,我们可以知道此时预测值是正确的,那么此时的 J ( θ ) = − l n ( h θ ( x ) ) J(\theta)=-ln(h_\theta(x)) J(θ)=−ln(hθ(x))的值就趋向于0。如果此时 h θ ( x ) → 0 h_\theta(x)\rightarrow0 hθ(x)→0,此时的预测值是错误的,那么此时的误差就趋向于无穷(由于 − l n ( x ) -ln(x) −ln(x)在 x → 0 x\rightarrow0 x→0时,值是无穷大的),此时我们给模型一个非常大的惩罚项,来逼迫模型修改参数来进行拟合。接下来分析 y = 0 y=0 y=0是的情况,为了方便理解,我们可以得到 − l n ( 1 − h θ ( x ) ) -ln(1-h_\theta(x)) −ln(1−hθ(x))的图像:
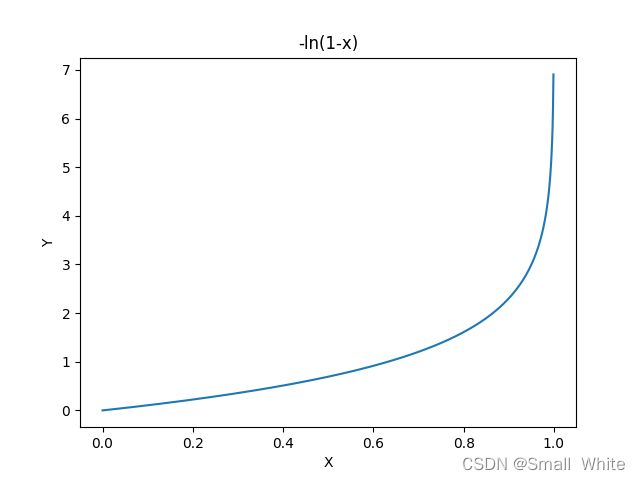
同样的,根据当 y = 0 y=0 y=0时的 J ( θ ) J(\theta) J(θ)图像, y = 0 y=0 y=0时的损失函数这样理解:当 y = 0 y=0 y=0时,如果此时的 h θ ( x ) → 0 h_\theta(x)\rightarrow0 hθ(x)→0,我们可以知道此时预测值是正确的,那么此时的 J ( θ ) = − l n ( 1 − h θ ( x ) ) J(\theta)=-ln(1-h_\theta(x)) J(θ)=−ln(1−hθ(x))的值就趋向于0。如果此时 h θ ( x ) → 1 h_\theta(x)\rightarrow1 hθ(x)→1,此时的预测值是错误的,那么此时的误差就趋向于无穷(由于 − l n ( 1 − x ) -ln(1-x) −ln(1−x)在 x → 1 x\rightarrow1 x→1时,值是无穷大的),此时我们给模型一个非常大的惩罚项,来逼迫模型修改参数来进行拟合。
注意:上述的分段函数再结合批量处理,我们可以合成一个下列损失函数:
J ( θ ) = 1 m ( ∑ i = 1 m ( − y ( i ) l n ( h θ ( x ( i ) ) ) − ( 1 − y ( i ) ) l n ( 1 − h θ ( x ( i ) ) ) ) (6) J(\theta) = \frac{1}{m}(\sum_{i=1}^{m}(-y^{(i)}ln(h_\theta(x^{(i)}))-(1-y^{(i)})ln(1-h_\theta(x^{(i)})))\tag{6} J(θ)=m1(i=1∑m(−y(i)ln(hθ(x(i)))−(1−y(i))ln(1−hθ(x(i))))(6) -
梯度下降
通过线性回归系列第一篇的介绍,线性回归的 θ \theta θ更新减去的值是对 J ( θ ) J(\theta) J(θ)求导的来的,下面是求导过程:
先求 ( l n ( h θ ( x ) ) ′ (ln(h_\theta(x))' (ln(hθ(x))′
( l n ( h θ ( x ) ) ′ = l n ( 1 1 + e − θ x ) ′ = 1 h θ ( x ) ( − e − θ x ( 1 + e − θ x ) 2 ) x = − h θ ( x ) e − θ x x = − h θ ( x ) ( 1 + e − θ x − 1 ) x = − h θ ( x ) ( 1 h θ ( x ) − 1 ) x = ( h θ ( x ) − h θ ( x ) 1 h θ ( x ) ) x = − ( 1 − h θ ( x ) ) x (ln(h_\theta(x))' = ln(\frac{1}{1+e^{-\theta x}})'\\=\frac{1}{h_\theta(x)}(-\frac{e^{-\theta x}}{(1+e^{-\theta x})^2})x \\ = - h_\theta(x)e^{-\theta x }x \\ = - h_\theta(x)(1+e^{-\theta x }-1)x \\ = - h_\theta(x)(\frac{1}{h_\theta(x)}-1)x \\ =( h_\theta(x)-h_\theta(x)\frac{1}{h_\theta(x)})x \\=-(1-h_\theta(x))x (ln(hθ(x))′=ln(1+e−θx1)′=hθ(x)1(−(1+e−θx)2e−θx)x=−hθ(x)e−θxx=−hθ(x)(1+e−θx−1)x=−hθ(x)(hθ(x)1−1)x=(hθ(x)−hθ(x)hθ(x)1)x=−(1−hθ(x))x
同样的再求 ( l n ( 1 − h θ ( x ) ) ′ (ln(1-h_\theta(x))' (ln(1−hθ(x))′
( l n ( 1 − h θ ( x ) ) ′ = 1 1 − h θ ( x ) ( e − θ x ( 1 + e − θ x ) 2 ) x = 1 1 − h θ ( x ) ( 1 + e − θ x − 1 ( 1 + e − θ x ) 2 ) x = 1 1 − h θ ( x ) ( h θ ( x ) − h θ 2 ( x ) ) x = 1 1 − h θ ( x ) h θ ( x ) ( 1 − h θ ( x ) ) x = h θ ( x ) x (ln(1-h_\theta(x))' = \frac{1}{1-h_\theta(x)}(\frac{e^{-\theta x}}{(1+e^{-\theta x})^2})x \\ = \frac{1}{1-h_\theta(x)}(\frac{1+e^{-\theta x}-1}{(1+e^{-\theta x})^2})x \\ = \frac{1}{1-h_\theta(x)}(h_\theta(x)-h^2_\theta(x))x \\ = \frac{1}{1-h_\theta(x)}h_\theta(x)(1-h_\theta(x))x \\ = h_\theta(x)x (ln(1−hθ(x))′=1−hθ(x)1((1+e−θx)2e−θx)x=1−hθ(x)1((1+e−θx)21+e−θx−1)x=1−hθ(x)1(hθ(x)−hθ2(x))x=1−hθ(x)1hθ(x)(1−hθ(x))x=hθ(x)x
接下来我们可以对 J ( θ ) J(\theta) J(θ)求导:
J ′ ( θ ) = − 1 m ( ∑ i = 1 m ( − y ( i ) ( − ( 1 − h θ ( x ( i ) ) ) x j ( i ) ) − ( 1 − y ( i ) ) h θ ( x ( i ) ) x j ( i ) ) = − 1 m ( ∑ i = 1 m ( y ( i ) x ( i ) − y ( i ) h θ ( x ( i ) ) x j ( i ) ) − ( h θ ( x ( i ) ) x ( i ) − y ( i ) h θ ( x ( i ) ) x j ( i ) ) = − 1 m ( ∑ i = 1 m ( y ( i ) x ( i ) − h θ ( x ( i ) ) x j ( i ) ) ) = − 1 m ( ∑ i = 1 m ( y ( i ) − h θ ( x ( i ) ) ) x j ( i ) = 1 m ( ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) J'(\theta) = -\frac{1}{m}(\sum_{i = 1}^{m}(-y^{(i)}(-(1-h_\theta(x^{(i)}))x_j^{(i)})\\-(1-y^{(i)})h_\theta(x^{(i)})x_j^{(i)}) \\ = -\frac{1}{m}(\sum_{i = 1}^{m}(y^{(i)}x^{(i)}-y^{(i)}h_\theta(x^{(i)})x_j^{(i)})\\-(h_\theta(x^{(i)})x^{(i)}-y^{(i)}h_\theta(x^{(i)})x_j^{(i)}) \\ = -\frac{1}{m}(\sum_{i = 1}^{m}(y^{(i)}x^{(i)}-h_\theta(x^{(i)})x_j^{(i)})) \\ = -\frac{1}{m}(\sum_{i = 1}^{m}(y^{(i)}-h_\theta(x^{(i)}))x_j^{(i)} \\ = \frac{1}{m}(\sum_{i = 1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} J′(θ)=−m1(i=1∑m(−y(i)(−(1−hθ(x(i)))xj(i))−(1−y(i))hθ(x(i))xj(i))=−m1(i=1∑m(y(i)x(i)−y(i)hθ(x(i))xj(i))−(hθ(x(i))x(i)−y(i)hθ(x(i))xj(i))=−m1(i=1∑m(y(i)x(i)−hθ(x(i))xj(i)))=−m1(i=1∑m(y(i)−hθ(x(i)))xj(i)=m1(i=1∑m(hθ(x(i))−y(i))xj(i)
最后我们可以惊讶的得到的下降梯度与线性回归是相同的,此时对于梯度下降函数可以这样定义:
θ j : = θ j − α 1 m ( ∑ x = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) ) (7) \theta_j := \theta_j - \alpha\frac{1}{m}(\sum_{x=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)})\tag{7} θj:=θj−αm1(x=1∑m(hθ(x(i))−y(i))xj(i))(7)
上面是关于逻辑回归的梯度下降的基本知识。 -
边界曲线
当我们指定 h θ ( x ) = 0.5 h_\theta(x) = 0.5 hθ(x)=0.5时作为阈值时,即 h θ ( x ) > 0.5 h_\theta(x) > 0.5 hθ(x)>0.5判定为1, h θ ( x ) ≤ 0.5 h_\theta(x) ≤ 0.5 hθ(x)≤0.5判定为0,从(1)式中我们可以得到当 z = θ T x = 0 z = \theta^T x = 0 z=θTx=0时,(1)式的值为0.5,即 h θ ( x ) = 0.5 h_\theta(x) = 0.5 hθ(x)=0.5,所以我们的边界曲线就是当 z = θ T x z = \theta^T x z=θTx为0时可得。例如: z = θ T x = θ 1 x 1 + θ 2 x 2 + θ 0 z = \theta^T x = \theta_1x_1+\theta_2x_2+\theta_0 z=θTx=θ1x1+θ2x2+θ0
此时的边界曲线是与 x 1 、 x 2 x_1、x_2 x1、x2相关的曲线: θ 1 x 1 + θ 2 x 2 + θ 0 = 0 \theta_1x_1+\theta_2x_2+\theta_0 = 0 θ1x1+θ2x2+θ0=0 -
高级优化方式
除了梯度下降时,我们有一些高级优化算法,可以自动帮助我们调整找合适的下降步长速率 α \alpha α,同时支持根据数据训练到损失函数最小,对于高级优化算法来讲,损失函数最小的评判标准是在进行训练时,损失函数有连续多次值不再下降。常见的高级优化算法有包括但不完全:
常见的优化方式 { 梯度下降 共轭梯度法 B F G S L − B F G C ⋯ 常见的优化方式\begin{cases} 梯度下降 \\ 共轭梯度法 \\ BFGS \\ L-BFGC \\ \cdots \end{cases} 常见的优化方式⎩ ⎨ ⎧梯度下降共轭梯度法BFGSL−BFGC⋯
由于逻辑回归的 α \alpha α与下降训练次数比较难确定,很难通过调整参数达到最优化,所以为了方便我们就采用高级优化方法。
二、代码实现
- 读取与处理数据、拟合图、误差图代码,文件名:
logisticpredict.py
from math import ceil
import scipy.optimize as opt
from time import process_time_ns
import numpy as np
import matplotlib.pyplot as plt
from logisticgredient import gredientFun
orig_data= np.loadtxt('ex2data1.txt',delimiter=',')
# 分出0的点与1的点
zero_data = orig_data[orig_data[:,2]==0]
one_data = orig_data[orig_data[:,2]==1]
zero_x_1 = zero_data[:,0]
one_x_1 = one_data[:,0]
zero_x_2 = zero_data[:,1]
one_x_2 = one_data[:,1]
theta = np.array([0,0,0])
# theta_0 = 0.1
# 80%训练数据,20% 测试数据
trans_data = orig_data[:int(0.8*(np.size(orig_data)/3))]
test_data = orig_data[-ceil(0.2*(np.size(orig_data)/3)):]
trans_data_x = trans_data[:,:2]
trans_data_y = trans_data[:,-1]
test_data_x = test_data[:,:2]
test_data_y = test_data[:,-1]
trans_one = np.ones((1,int(np.size(trans_data_y))))
test_one = np.ones((1,int(np.size(test_data_y))))
test_data_x = np.insert(test_data_x,0,values=test_one,axis=1)
trans_data_x = np.insert(trans_data_x,0,values=trans_one,axis=1)
error_array_show = np.array([])
def cost(theta,trans_data_x,trans_data_y):
global error_array_show
theta_data_x = np.dot(theta,trans_data_x.T) #+theta_0
error_y = 1/(1+np.exp(-theta_data_x))
# error_j = np.sum((np.multiply(-trans_data_y,np.log(error_y))-np.multiply((1-trans_data_y),np.log(1-error_y)))/np.size(trans_data_y)) 这个也是可以的
error_j = (np.dot(trans_data_y,np.log(error_y).T)+np.dot((1-trans_data_y),np.log(1-error_y).T))/(-np.size(trans_data_y))
error_array_show=np.concatenate((error_array_show,np.array([error_j])),axis=0)
return error_j
# 此处是高级算法,第一个参数是损失函数,第二个是参数,第三个是梯度函数,第四个是训练集
result = opt.fmin_tnc(func=cost,x0=theta,fprime=gredientFun,args=(trans_data_x,trans_data_y))
theta = result[0]
y = np.dot(theta,trans_data_x.T)
x_1_range = np.linspace(30, 100, 100)
x_2_range = (theta[1]*x_1_range+theta[0])/(-theta[2])
x_axis = np.arange(np.size(error_array_show)).reshape(np.size(error_array_show),1)
print(error_array_show)
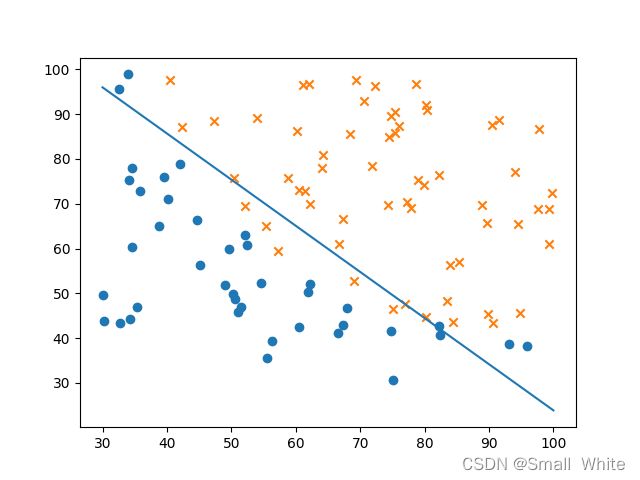
plt.scatter(zero_x_1,zero_x_2,marker='o')
plt.scatter(one_x_1,one_x_2,marker='x')
plt.plot(x_1_range,x_2_range)
plt.show()
plt.figure()
plt.plot(x_axis,error_array_show)
plt.show()
#测试集
test_result = 1/(1+np.exp(-np.dot(theta,test_data_x.T)))
count = 0
for i in range(np.size(test_result)):
if test_result[i]>0.5:
if test_data_y[i]==1:
count+=1
if test_result[i]<=0.5:
if test_data_y[i]==0:
count+=1
print('准确率为{}%'.format((count/np.size(test_data_y))*100))
- 下面是梯度函数,文件名为:
logisticgredient.py
import numpy as np
def gredientFun(theta,trans_data_x,trans_data_y):
alpha = 0.009
# theta_0 = theta_0 - alpha * (np.sum(error_array)/np.size(error_array))
theta_data_x = np.dot(theta,trans_data_x.T) #+theta_0
error_y = 1/(1+np.exp(-theta_data_x)) - trans_data_y
gradient=(np.dot(error_y,trans_data_x)/np.size(error_y))
print('theta为{}'.format(theta))
return gradient
三、样本集
复制放进txt中即可
34.62365962451697,78.0246928153624,0
30.28671076822607,43.89499752400101,0
35.84740876993872,72.90219802708364,0
60.18259938620976,86.30855209546826,1
79.0327360507101,75.3443764369103,1
45.08327747668339,56.3163717815305,0
61.10666453684766,96.51142588489624,1
75.02474556738889,46.55401354116538,1
76.09878670226257,87.42056971926803,1
84.43281996120035,43.53339331072109,1
95.86155507093572,38.22527805795094,0
75.01365838958247,30.60326323428011,0
82.30705337399482,76.48196330235604,1
69.36458875970939,97.71869196188608,1
39.53833914367223,76.03681085115882,0
53.9710521485623,89.20735013750205,1
69.07014406283025,52.74046973016765,1
67.94685547711617,46.67857410673128,0
70.66150955499435,92.92713789364831,1
76.97878372747498,47.57596364975532,1
67.37202754570876,42.83843832029179,0
89.67677575072079,65.79936592745237,1
50.534788289883,48.85581152764205,0
34.21206097786789,44.20952859866288,0
77.9240914545704,68.9723599933059,1
62.27101367004632,69.95445795447587,1
80.1901807509566,44.82162893218353,1
93.114388797442,38.80067033713209,0
61.83020602312595,50.25610789244621,0
38.78580379679423,64.99568095539578,0
61.379289447425,72.80788731317097,1
85.40451939411645,57.05198397627122,1
52.10797973193984,63.12762376881715,0
52.04540476831827,69.43286012045222,1
40.23689373545111,71.16774802184875,0
54.63510555424817,52.21388588061123,0
33.91550010906887,98.86943574220611,0
64.17698887494485,80.90806058670817,1
74.78925295941542,41.57341522824434,0
34.1836400264419,75.2377203360134,0
83.90239366249155,56.30804621605327,1
51.54772026906181,46.85629026349976,0
94.44336776917852,65.56892160559052,1
82.36875375713919,40.61825515970618,0
51.04775177128865,45.82270145776001,0
62.22267576120188,52.06099194836679,0
77.19303492601364,70.45820000180959,1
97.77159928000232,86.7278223300282,1
62.07306379667647,96.76882412413983,1
91.56497449807442,88.69629254546599,1
79.94481794066932,74.16311935043758,1
99.2725269292572,60.99903099844988,1
90.54671411399852,43.39060180650027,1
34.52451385320009,60.39634245837173,0
50.2864961189907,49.80453881323059,0
49.58667721632031,59.80895099453265,0
97.64563396007767,68.86157272420604,1
32.57720016809309,95.59854761387875,0
74.24869136721598,69.82457122657193,1
71.79646205863379,78.45356224515052,1
75.3956114656803,85.75993667331619,1
35.28611281526193,47.02051394723416,0
56.25381749711624,39.26147251058019,0
30.05882244669796,49.59297386723685,0
44.66826172480893,66.45008614558913,0
66.56089447242954,41.09209807936973,0
40.45755098375164,97.53518548909936,1
49.07256321908844,51.88321182073966,0
80.27957401466998,92.11606081344084,1
66.74671856944039,60.99139402740988,1
32.72283304060323,43.30717306430063,0
64.0393204150601,78.03168802018232,1
72.34649422579923,96.22759296761404,1
60.45788573918959,73.09499809758037,1
58.84095621726802,75.85844831279042,1
99.82785779692128,72.36925193383885,1
47.26426910848174,88.47586499559782,1
50.45815980285988,75.80985952982456,1
60.45555629271532,42.50840943572217,0
82.22666157785568,42.71987853716458,0
88.9138964166533,69.80378889835472,1
94.83450672430196,45.69430680250754,1
67.31925746917527,66.58935317747915,1
57.23870631569862,59.51428198012956,1
80.36675600171273,90.96014789746954,1
68.46852178591112,85.59430710452014,1
42.0754545384731,78.84478600148043,0
75.47770200533905,90.42453899753964,1
78.63542434898018,96.64742716885644,1
52.34800398794107,60.76950525602592,0
94.09433112516793,77.15910509073893,1
90.44855097096364,87.50879176484702,1
55.48216114069585,35.57070347228866,0
74.49269241843041,84.84513684930135,1
89.84580670720979,45.35828361091658,1
83.48916274498238,48.38028579728175,1
42.2617008099817,87.10385094025457,1
99.31500880510394,68.77540947206617,1
55.34001756003703,64.9319380069486,1
74.77589300092767,89.52981289513276,1
以上若有问题,请大佬指出,感激不尽,共同进步。