【计算机图形学】基础 - Colorization using Optimization

1. 已存在的问题

传统的Colorization方法通常涉及到将图像划分为多个区域，并跨图像序列跟踪这些区域。然而这两个任务在实践中的成果是非常不可靠的。
Colorization原本是一个耗费大量人力、花费较多时间的任务。且上边提到的“将图像划分为多个区域”常采用自动分割算法，但已存在的自动分割算法无法正确区分模糊或复杂的区域边界，故也导致传统的基于这种自动分割算法的Colorization是十分不准确的。

2. 文章目标

文章的目标是提出一个简单的Colorization方法，这种方法既不需要精确的图像分割，也不需要精准的图像追踪。这种应方法基于一个统一的框架，却能够同时应用在静态图像和图像序列之上。

3. 文章算法

3.1 文章相关定义与所需知识

文章算法工作在YUV空间下。其中，Y表示的是单色亮度通道，简称为“亮度”；U和V表示色度通道，用来编码颜色。
LU分解：可以用于求解线性方程组。

3.2 算法

将一个亮度体积Y(x,y,t)作为输入，将两个颜色体积U(x,y,t)和V(x,y,t)作为输出。为了方便起见，下文中使用r和s来表示(x,y,t)三元组。
文章的算法基于一个简单的前提：在时间和空间上具有相似灰度等级的像素也会具有相同的颜色。换句话来说，如果两个像素r和s具有相似的亮度，则他们也会有相似的颜色。因此，我们希望能够通过最小化在像素r上的颜色U®与相邻像素颜色加权平均值的差异：

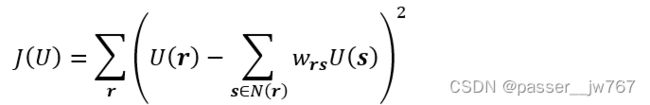
在这里，w_rs是r周围点的权重，权重之和为1。当Y®与Y(s)相似时，权重w_rs就会稍大一些，反之则反。
类似的，对于颜色V®的优化我们也可以列出类似的式子。
其中，因为上边提到的权重系数w_rs是根据Y的变化进行变化的，故可以通过Y通道进行表示。文章尝试了两种不同的加权函数，分别如式(2)和式(3)表示。其中，式(2)常用于图像分割算法，是基于两个亮度之间的平方差来定义的。

还有一种加权函数是基于两个亮度之间的归一化相关性进行定义的：

在这两个式子中，μ_r和σ_r分别是r窗口强度的平均值和方差。根据式(2)、(3)，只要给定了像素的位置和关系，我们便能够轻松地求出这个系数。
相关亲和力也可以通过假设颜色和强度之间的局部线性关系来得到。形式上，假设像素的颜色U®是亮度Y®的线性函数：U®=a_i Y®+b_i。这里的线性系数a_i和b_i在r附近所有的像素都是相同的。当我们在每个模型的窗口间增加一对变量时，简单地消除a_i,b_i变量，得到一个具有相关亲和函数的等价方程。
符号r∈N(s)表示r和s是相邻的像素。在单个帧中，若两个像素的图像位置是相邻的，则我们将它们定义为邻居。在两个连续的帧中，如果它们在考虑运动之后图像位置是相邻的，则我们定义这两个像素为邻居。我们用v_x (x,y),v_y (x,y)来表示时间t时刻计算出的光流，若满足式(4)，则像素(x_0,y_0,t)是像素(x_1,y_1,t+1)的邻居：

光流场v_x (x_0 ),v_y (y_0)使用标准的运动估计算法来计算。但此处光流场仅用于定义每个像素的领域关系，而不会用于颜色的传播。

3.3 方程的求解

现在给定了一组位置r_i，颜色则通过u(r_i )=u_i,v(r_i )=v_i进行指定。我们在这样的条件下去最小化如式(1)所示的J(U),J(V)。由于成本函数是二次的，而约束是线性的，故这个优化问题会产生一个大型的稀疏线性方程组，能够使用许多标准的方法进行求解。
参考图像处理其他任务中的算法，比如在基于归一化切割的图像分割算法中，人们就尝试去寻找矩阵D-W的第二小的特征向量。其中W是n像素×n像素的矩阵，矩阵W中的元素则表示像素之间的亲和性，即在3.2中所提到的w_rs。而D是一个对角矩阵，其对角线元素是亲和力的和。
对于任意的对称矩阵A来说，第二小的特征向量是使得x^T Ax最小化并同时与第一小特征向量正交的向量x。经直接检验，归一化切割的二次型就是文章提出的成本函数J，即x^T (D-W)=J(x)。

4. 文章贡献

文章提出了一种能够帮助图像艺术家以花费更少的精力给电影上色的方法。艺术家并不需要描绘出具体的边界，而只需要选定少量的帧进行染色，文章会按一种尊重亮度边界的算法对艺术家涂抹的颜色进行传播。

5. 代码实现

5.1 环境配置

Python3.9.12
opencv-python4.6.0.66
scipy1.7.3
scikit-learn1.0.2

5.2 代码实现

源代码如下：

import os
import cv2 as cv
import numpy as np
from scipy import sparse
from sklearn.preprocessing import normalize

# 注：opencv读取图片的顺序是BGR
def rgb2yuv(rgb):
    rgb = rgb / 255.0
    y = np.clip(np.dot(rgb, np.array([0.299, 0.587, 0.144])),             0,   1)
    u = np.clip(np.dot(rgb, np.array([0.595716, -0.274453, -0.321263])), -0.5957, 0.5957)
    v = np.clip(np.dot(rgb, np.array([0.211456, -0.522591, 0.311135])),  -0.5226, 0.5226)
    yuv = rgb
    yuv[:, :, 0] = y
    yuv[:, :, 1] = u
    yuv[:, :, 2] = v
    return yuv

def yuv2rgb(yuv):
    r = np.dot(yuv, np.array([1.0,  0.956295719758948,  0.621024416465261]))
    g = np.dot(yuv, np.array([1.0, -0.272122099318510, -0.647380596825695]))
    b = np.dot(yuv, np.array([1.0, -1.106989016736491,  1.704614998364648]))
    rgb = yuv
    rgb[:, :, 0] = r
    rgb[:, :, 1] = g
    rgb[:, :, 2] = b
    rgb = np.clip(rgb, 0.0, 1.0) * 255.0
    return rgb

# 找到有涂抹颜色的位置
def find_marked_locations(src, marked):
    diff = marked - src
    # idx = (*np.nonzero(diff[:, :, i]) for i in [1, 2])
    # colored = set(zip(idx))
    colored = [set(zip(*np.nonzero(diff[:, :, i]))) for i in [1, 2]]
    return colored[0].union(colored[1])

# 该函数用于取出矩阵X中像素pixel的neighbor
def neighborhood(X, loc):
    # 这里对于Wright和Hbottom需要+2是因为这个loc取的是pixel的左上角，当我们想要取到这个window的边界，就需要跨两个pixel
    Wleft = max(loc[0] - 1, 0)
    Wright = min(loc[0] + 2, X.shape[0])
    Htop = max(loc[1] - 1, 0)
    Hbottom = min(loc[1] + 2, X.shape[1])
    return X[Wleft: Wright, Htop: Hbottom]

# 计算r及其neighbor的方差
def std_matrix(A):
    W = np.zeros_like(A)
    for i in range(A.shape[0]):
        for j in range(A.shape[1]):
            W[i, j] = np.square(np.std(neighborhood(A, [i,j])))
    return W

# 计算Wrs的权重函数
def weight(r, N, Y, S):
    return [np.exp(-1 * np.square(Y[r] - Y[n]) / (2 * S[r])) if S[r] > 0.0 else 0.0 for n in N]

def cartesian(arrays, out=None):
    arrays = [np.asarray(x) for x in arrays]
    dtype = arrays[0].dtype

    n = np.prod([x.size for x in arrays])
    if out is None:
        out = np.zeros([n, len(arrays)], dtype=dtype)

    m = n // arrays[0].size
    out[:,0] = np.repeat(arrays[0], m)
    if arrays[1:]:
        cartesian(arrays[1:], out=out[0:m,1:])
        for j in range(1, arrays[0].size):
            out[j*m:(j+1)*m,1:] = out[0:m,1:]
    return out

# 用于建立Wrs矩阵
def build_weight_matrix(Y):
    (width, height) = [Y.shape[0], Y.shape[1]]
    # 求方差
    S = std_matrix(Y)
    img_size = width * height
    cart = cartesian([range(width), range(height)])
    cart_r = cart.reshape(width, height, 2)
    xy2idx = np.arange(img_size).reshape(width, height)
    # lil_matrix，可以提升访问速度
    W = sparse.lil_matrix((img_size, img_size))
    for i in range(Y.shape[0]):
        print("i:" + str(i))
        for j in range(Y.shape[1]):
            idx = xy2idx[i, j]
            N = neighborhood(cart_r, [i, j]).reshape(-1, 2)
            N = [tuple(neighbor) for neighbor in N]
            N.remove((i, j))
            p_idx = [xy2idx[xy] for xy in N]
            weights = weight((i, j), N, Y, S)
            W[idx, p_idx] = -1 * np.asmatrix(weights)
            del N, idx, p_idx, weights 

    Wrs = normalize(W, norm='l1', axis=1)
    Wrs[np.arange(img_size), np.arange(img_size)] = 1

    return Wrs

def mainFunc():
    # 读取图片
    src_fileName = "baby.bmp"
    marked_fileName = "baby_marked.bmp"
    
    src_img_rgb = cv.imread(os.path.join('samples/', src_fileName))
    marked_img_rgb = cv.imread(os.path.join('samples/', marked_fileName))

    # 由于opencv读的时候建立的img都是RGB通道的，我们需要将其转换为YUV通道
    src_img = rgb2yuv(src_img_rgb)
    marked_img = rgb2yuv(marked_img_rgb)

    # 把Y通道提取出来
    Y = np.array(src_img[:, :, 0], dtype='float64') # shape: [H, W]

    # 获取图片的宽(W-x)高(H-y)
    height, width = np.shape(src_img)[0:2]
    img_size = height * width
    
    # 建立权重矩阵Wrs
    W = build_weight_matrix(Y)

    # 通过比较src_img和marked_img的差异，找到被涂抹了颜色的部分，得到的结果是一个，记录了被涂抹的区域
    colored = find_marked_locations(src_img, marked_img)

    # 在需要对稀疏矩阵的元素值做大量访问时,首先将待访问的稀疏矩阵做一个转换.tolil()是非常必要的,13000次访问测试,链表稀疏矩阵lil则在50ms内就完成
    # 列压缩稀疏矩阵csc是非常慢的
    W = W.tolil()

    # 做一个index索引矩阵
    xy2idx = np.arange(img_size).reshape(height, width)

    # 对有颜色涂抹的区域进行遍历
    for idx in [xy2idx[i, j] for [i, j] in colored]:
        # csr_matrix压缩矩阵
        W[idx] = sparse.csr_matrix(([1.0], ([0], [idx])), shape = (1,img_size))
    
    LU = sparse.linalg.splu(W.tocsc())

    U = LU.solve((marked_img[:, :, 1]).flatten())
    V = LU.solve((marked_img[:, :, 2]).flatten())

    result = np.zeros_like(src_img)
    result[:, :, 0] = Y
    result[:, :, 1] = U.reshape((height, width))
    result[:, :, 2] = V.reshape((height, width))
    result = yuv2rgb(result)

    cv.imwrite("result.bmp", result)

if __name__ == '__main__':
    mainFunc()

5.3 结果展示

顶部为原始图片，中间图片为涂抹颜色的图片，最下边为代码运行结果，注意中间涂抹颜色的图片有个黄颜色的小点（可能不是很清楚，可以放大看）。
下边最顶上的图为原始图片，第二张图为涂抹颜色的图片，最下方为代码运行结果。

6. 学习总结

这一次学习的这篇paper的思想和算法都并不复杂。只是在尝试自己写文章的代码时候，总是会报一些错误，所以这段代码我陆陆续续写了三四天，期间还需要上网去查找一些相关的矩阵运算函数。一开始跑代码的时候，不仅十分占内存，而且耗费的时间也很长（320×265像素的图像花费的时间大约要半个多小时），后来才知道有一种.tolil()函数能够加快对矩阵的访问，从而降低了运行时间。总之，虽然这次写代码花费了不少的时间，但是体会还是比较深的，了解了以前不知道的一些函数，也掌握了更进一步的知识。

Reference

[1] A. Levin D. Lischinski and Y. Weiss Colorization using Optimization.SIGGRAPH, ACM Transactions on Graphics, Aug 2004.
[2] 读源码学算法之Colorization
[3] 机器学习：Colorization using Optimization
[4] scpiy: sp.tolil()
[5] 矩阵的LU分解
[6] 矩阵分解（1）-- 矩阵分解之LU分解