图像处理——采样与量化

---

前言

从广义上说，图像是自然界景物的客观反映。以照片形式或视频记录介质保存的图像是连续的，计算机无法接收和
处理这种空间分布和亮度取值均连续分布的图像。图像数字化就是将连续图像离散化，其工作包括两个方面：
取样和量化。

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、连续图像和离散图像

连续图像：二维坐标系中具有连续变化的，即图像画面的像素点是无限稠密的，同时其灰度值（即图像从暗到亮的变化值）也是无限稠密的图像，成为连续图像。连续图像又成为模拟图像。

离散图像：是指用一个数字阵列表示的图像。该阵列中每一个元素成为像素。离散图像又称数字图像。

获取图像（acquire image）就是将连续图像转换为数字（离散）图像Continuous To Discrete Conversion**
图像的获取即图像的数字化过程（Digital Imaging）：扫描，采样，量化

二、采样（sampling）

设连续图像f(x,y)经过数字化后，可以用一个离散量组成的矩阵g(i,j)即二维数组来表示。

g(i,j)代表的点（i,j）即为采样点（sampling point），也称灰度值。
数字化采样一般是按照正方形点阵取样的，也有三角形点阵，正六角形点阵取样，采样点在平面上的几何关系如图所示，成为栅格（grid）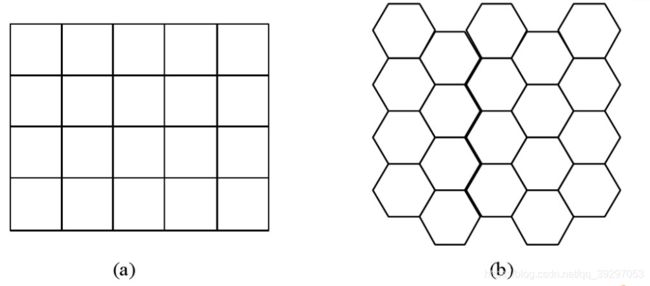
全体像素覆盖了整个图像，实际的数字转换器捕捉的像素具有有限尺寸（这是因为采样函数不是一组理性的狄拉克冲击，而是一组有限冲击），从图像分析角度看，像素是不可再分割的单位。

三，图像的频域

一、图像高频信号和低频信号的理解
1.1 图像中的低频信号和高频信号也叫做低频分量和高频分量。
1）空间频率指的是图像中灰度值相对它的邻居点变化方式。如果一副图像中灰度从一边到另一边变化很小，那就说这副图像是低频信号。如果某些像素相对于它邻近的像素点变化很剧烈，则说明该图像含有高频信号.
2）简单一点说，图像中的高频分量，指的是图像强度（亮度/灰度）变化剧烈的地方，也就是我们常说的边缘（轮廓）；图像中的低频分量，指的是图像强度（亮度/灰度）变换平缓的地方，也就是大片色块的地方。人眼对图像中的高频信号更为敏感。
3）图像的高低频是对图像各个位置之间强度变化的一种度量方法。

低频分量：主要对整副图像的强度的综合度量。
高频分量：主要是对图像边缘和轮廓的度量。
如果一副图像的各个位置的强度大小相等,则图像只存在低频分量,从图像的频谱图上看,只有一个主峰,且位于频率为零的位置。 如果一副图像的各个位置的强度变化剧烈,则图像不仅存在低频分量,同时也存在多种高频分量,从图像的频谱上看,不仅有一个主峰,同时也存在多个旁峰。

1.2直观认识
假设在正弦波中有一个毛刺，并且正弦波的变化非常的缓慢，频率较低，在正弦波上有一个毛刺，这个毛刺在短时间内就完成了一个变化周期，频率较高。所以我们就把这里的正弦波称为低频信号，而毛刺就称为高频信号。如果要对这个曲线平滑滤波的话，效果就是把毛刺滤掉，也就是说，平滑滤波的操作会将高频信号去除而低频信号保留，也就是我们常说的低通滤波器了。 最简单的低通滤波器的实现就是中值或者均值滤波器。 由以上的认识推广到二维图像上，也就不难知道为什么会将图像上变化剧烈的地方叫做高频信号，而变化平缓的地方叫做低频信号了。

二、图像频率的理解
1、不同频率信息在图像结构中有不同的作用。图像的主要成分是低频信息，它形成了图像的基本灰度等级，对图像结构的决定作用较小；中频信息决定了图像的基本结构，形成了图像的主要边缘结构；高频信息形成了图像的边缘和细节，是在中频信息上对图像内容的进一步强化。
2、图像的频率是表征图像中灰度变化剧烈程度的指标，是灰度在平面空间上的梯度。如：大面积的沙漠在图像中是一片灰度变化缓慢的区域，对应的频率值很低；而对于地表属性变换剧烈的边缘区域在图像中是一片灰度变化剧烈的区域，对应的频率值较高。
3、对图像而言，图像的边缘部分是突变部分，变化较快，因此反应在频域上是高频分量；图像的噪声大部分情况下是高频部分；图像平缓变化部分则为低频分量。也就是说，傅立叶变换提供另外一个角度来观察图像，可以将图像从灰度分布转化到频率分布上来观察图像的特征。
4、图像进行二维傅立叶变换得到频谱图，就是图像梯度的分布图，当然频谱图上的各点与图像上各点并不存在一一对应的关系，即使在不移频的情况下也是没有。傅立叶频谱图上我们看到的明暗不一的亮点，实际是上图像上某一点与邻域点差异的强弱，即梯度的大小，也即该点的频率的大小（可以这么理解，图像中的低频部分指低梯度的点，高频部分相反）。
5、图像的频率，不是图像上某一个点的频率，它反映了反应了图像像素变化的快慢，也就是说，在某一区域变化的非常大非常的快，那这一区域就携带有一定的高频的信息。图像的高频信息越多，图像的细节特征也就越多。
三、各类滤波器
高通滤波：允许高频信号通过（边缘加强、提取）；
低通滤波：允许低频信号通过（边缘平滑）；
带通滤波：允许一定频率的信号通过；
带阻滤波：注意一定频率通过，并允许其他频率通过；
全通滤波：允许所有频率通过，仅仅改变相位关系；
陷波滤波（Band-Stop Filter）：阻止一个狭窄频率范围通过，一种特殊的带阻滤波器；

边缘区域的灰度变化较大，也就是频率较高，所以对于高通滤波边缘部分将会保留，非边缘部分将会被过滤；对于低通滤波边缘区域将会被平滑过渡掉。(低通即为模糊，高通即为锐化)
线性滤波是指：两个信号之和的响应和它的响应之和相等，即，每个像素的输出值是一些输入像素的加权和。

采用评价参数与定理

连续图像经过采样之后所获得的数字图像的效果与以下几个评价参数有关。
图像分辨率:采样所获得的图像总像素的多少。(如数码相机的30万像素)
采样密度:图像上单位长度所包含的采样点数。采样密度的倒数是采样间隔。
采样频率:是指一秒钟内采样的的次数。它反映了采样点之间的间隔大小,采样频率越高,丢失的信息越少,采样出的样本细腻逼真图像的质量好,但要求的存储量越大。(图像大小:对一幅图像采样时,若每行(即横向)像素为M个,每列(即纵向)像素为N个,则图像大小为MXN个像素。)

无论采用那种评价参数,都反映采样点间隔的选取是个很重要的问题。
显然,想要获得更加清晰的图像质量,就要提高图像采样像素点数,也就是要使用更多的像素点来表示该图像,但是相对要付出更大存储空间的代价釆样间隔的大小取决于原图像的细微亮暗变化。
从频域的角度来看采样问题:根据尼奎斯特采样定理（Nyquist sampling theorem）,若维信号g(t)的最大截止频为W,以,则T<=1/2W为采样间隔进行采样,则能够根据采样结果g(nt)完全恢复g(t)。

由采样定理可知,要想无失真的恢复一幅图像,采样频率应该大于图像模拟信号最高频率的2倍。如果采样频率低于原信号最高频率的2倍,则恢复的信号中会包含原信号中不存在的低频成分,称为混淆,它会对信号造成干扰。
釆样傅里叶变换,可以获得信号的频谱,并从中得知信号最高频率的数值。

---

四，量化（quantization）

模拟图像经过采样后,在时间和空间上离散化为像素。但采样所得的像素值(即灰度值)仍是连续量。把采样后所得的各像素的灰度值从模拟量到离散量的转换称为图像灰度的量化。图2-3(a)说明了量化过程。若连续灰度值用z来表示,对于满足≤x≤x的z值,都量化为整数q;。q称为像素的灰度值,z与q的差称为量化误差。一般,像素值量化后用一个字节8bit来表示。如图2-3(b)所示,把由黑—灰—白的连续变化的灰度值,量化为0-255共256级灰度值,灰度值的范围为0~255,表示亮度从深到浅,对应图像中的颜色为从黑到白。
连续灰度值量化为灰度级的方法有两种,一种是等间隔量化,另一种是非等间隔量化。等间隔量化就是简单地把采样值的灰度范围等间隔地分割并进行量化。对于像素灰度值在黑—白范围较均匀分布的图像,这种量化方法可以得到较小的量化误差。该方法也称为均匀量化或线性量化。为了减小量化误差,引入了非均匀量化的方法。非均匀量化是依据一幅图像具体的灰度值分布的概率密度函数,按总的量化误差最小的原则来进行量化。具体做法是对图像中像素灰度值频繁岀现的灰度值范围,量化间隔取小些,而对那些像素灰度值极少出现的范围,则量化间隔取大些。由于图像灰度值的概率分布密度函数因图像不同而异,所以不可能找到一个适用于各种不同图像的最佳非等间隔量化方案因此,实用上一般都采用等间隔量化

五，采样与量化的参数选择

幅图像在采样时,行、列的采样点与量化时每个像素量化的级数,既影响数字图像的质量,也影响到该数字图像数据量的大小。假定图像取M×N个样点,每个像素量化后的灰度进制位数为Q,一般Q总是取为2的整数幂, 则存储一幅数字图像所需的二进制位数b为
字节数B为

对一幅图像,当量化级数Q一定时,采样点数M×N对图像质量有着显著的影响。如图2-4所示,采样点数越多,图像质量越好;当采样点数减少时,图上的块状效应就逐渐明显。同理当图像的采样点数一定时,采用不同量化级数的图像质量也不样。如下图所示,量化级数越多,图像质量越好,当量化级数越少时,图像质量越差,量化级薮最小的极端情况就是二值图像,图像出现假轮廓。

可采用如下原则
(1)对缓变的图像,应该细量化,粗采样,以避免假轮廓（False contour）假轮廓意味着噪声大（noise）。
(2)对细节丰富的图像,应细采样,粗量化,以避免模糊(混叠：Aliasing)。
采样必须满足奈奎斯特取样定理,否则会因取样点数不够产生混淆失真。
对于彩色图像,是按照颜色成分—红®、绿(G)蓝(B)分别采样和量化的。若各种颜色成分均按8bit量化,即每种颜色量级别是256,则可以处理256×256×256=16777216种颜色。

六，数学基础