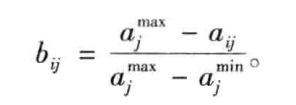综合评价与决策模型

本文的思想和内容参考：数学建模清风、司守奎《数学建模算法与应用》 第2版，改成转载需要给出原创链接，实属无意冒犯。

综合评价与决策模型

先上大纲

解决评价类问题的中心思想就是打分，首先要想到这四项内容：

1. 明确评价目标
2. 明确可选方案
3. 明确评价指标，形成评价体系（用什么来评价方案的好坏？）
4. 计算出得分，也就是综合评价指数，按排序指标值对方案进行排序，选出最优方案。

第三项，评价的指标，有时需要我们自己来确定，比如2021亚太杯C题对塞罕坝对生态环境的价值评估，就需要我们自己确定指标，可以先主观选取大概的指标，再用客观方法筛选更能反应系统特征的指标（主成分分析法、典型相关分析法）。根据题目背景材料、生活常识、网上搜集到的材料筛选合适的指标。可以爬取知网上相关文献的关键词。

模型的建立与求解步骤

拿到一个数据，我们一般是在列好评价体系表之后，即确定了有多少个指标和多少个待评价对象，首先进行正向化处理，即将所有指标转化为极大型，然后对正向化的矩阵进行标准化处理，即消除量纲的影响，其次对标准化后的矩阵进行归一化处理，归一化的目的是让我们的结果更加容易解释，或者说让我们对结果有一个更加清晰直观的印象。

向量规范化处理（这一步其实可以当成是正向化处理和标准化处理这两步的平替）。

数据预处理

假设现在有n个要评价的对象，m个评价指标，我们要做的就是把评价指标（又称属性值）规范化，这一步的目标是使得任一指标下性能约优的方案变化后的指标值越大（也就是得分值越大），并消除量纲的影响，以及为了便于多属性决策，而对属性值表中不同指标的属性值归一化。

1. 线性变换
   
2. 标准0-1变换
   
3. 区间型属性的变换
   
4. 向量规范化

5. 标准化处理

此外，要解决某些目标的达到程度与属性值之间的非线性关系，以及目标间的不完全补偿性，我们要采用非线性变换或者其它方法。

模型的量化与处理

确定指标权重

层次分析法
熵权法

指标评价等级的量化

如A-B-C-D量化为0.5-0.3-0.15-0.05（A+B+C+D = 1）

建立评价模型

主要是根据问题分析来建立合适的模型。

层次分析法（AHP）

一种系统分析与决策的综合评价方法，较合理的解决了定性问题定量化的处理过程。
主要实现：建立递阶层次结构，把主观判断转化到若干因素两两重要程度的比较上，从而把难以量化的定性判断转化为可操作的重要度的比较上面。

应用场景

最佳方案的选取

指标体系的优选

解决评价类问题（哪种方案最好、评价员工业绩等）

优缺点

优点：体现了人类决策思维的基本特征，分解-判断-综合

缺点：评价的决策层不能太多，太多的话判断矩阵和一致性矩阵的差异可能会很大。

主观性比较强，难以得到具有较强说服力的判断矩阵。

步骤（这里假设有3个方案，5个指标）

1. 建立层次结构模型（目标层➡准则层➡方案层）

2. 构造准则层➡方案层的判断矩阵（正互反矩阵，$aij\ast aji=1$）。判断矩阵的个数由方案层的方案个数决定。

   标度	含义
   1	同样重要性
   3	稍微重要
   5	明显重要
   7	强烈重要
   9	极端重要
   2, 4, 6, 8	上述两相邻判断的中值
   倒数	A和B相比如果标度为3， 那么B和A相比就是1/3

   方案i	准则1	准则2	准则3	准则4	准则5
   准则1
   准则2
   准则3
   准则4
   准则5

   准则i	方案1	方案2	方案3
   方案1
   方案2
   方案3

3. 一致性检验：检验判断矩阵（正互反矩阵）是否是一致矩阵（$aij\ast ajk=aik$）

   1. 计算一致性指标CI

   2. 查表看CI对应的平均随机一致性指标RI

   3. 计算一致性比例CR = CI/RI，小于1则符合一致性

4. 通过一致矩阵（通过一致性检验后的判断矩阵）计算权重，并将权重填入权重表。

   权重计算方法：

   • 算术平均法
   • 几何平均法
   • 特征值法

   指标权重计算	方法1	方法2	方法3
   指标（1-5）	算术平均法	几何平均法	特征值法
   指标1
   指标2
   指标3
   指标4
   指标5

   方案权重（得分）计算	方法1	方法2	方法3
   方案（1-3）	算术平均法	几何平均法	特征值法
   方案1
   方案2
   方案3

   将结果汇总到权重矩阵：

   指标	指标权重	方案1权重	方案2权重	方案3权重
   指标1
   指标2
   指标3
   指标4
   指标5

   根据权重矩阵，计算出每个方案的得分，并进行排序。

熵权法

理论依据：指标的变异程度越小，所反应的信息量也越小，其对应的权值也应该越低。（从数据本身来获取权值）。

首先我们来明确这几个概念：

1. 信息量

   一个事件x的信息量$I(x)$，与它发生的概率$P(x)$关系式为：$I(x)=-ln(P(x))$

2. 信息熵（归一化之后可以得到指标的熵权）

   $H(x)$，与信息量成反比，$H(x)={\sum }_{i=1}^n[P(x)I(x)]$，
   可以看出信息熵的本质就是信息量的期望值。且当每件事件的发生概率都想等即为$\frac{1}{n}$时，信息熵越大。

3. 信息效用值：与信息量成正比

为什么存在这个反比正比关系，可以看后面的步骤说明再来思考这个问题。

tips：越有可能发生的事，信息量就越小，越不可能发生的事，信息量就越多。对于熵权法而言，随机变量的信息熵越大，表示我们现有的信息量越小。信息熵反应的应该是在已有信息量的基础上，增加信息量所带来的价值，当然是你知道的越少，给你再补充点儿信息，你将会更有收获啦（这和我们初中学的画圆圈一个道理，一个人的知识面越大，他反而会觉得自己懂得更少，但是他已经有的知识的价值肯定是和知识面（量）成正比，也就是这里提到的信息效用值）。所以指标的信息熵越小，提供的信息量就越大。

应用场景

确定指标的权重

优缺点

优点：克服了层次分析法主观性较强所带来的结果不准确性

缺点：对于那些本身就发生概率较小 但根据常识来看 应该是要在评价决策时 占有较高的判断力的指标，在利用熵权法确定权重时，于其分配的权重比主观判断下要小得多。比如在评三好学生时，有违规这个指标，但大家基本上都不违规，也就是说在这个指标下，学生的得分都为0（正向化之后的得分），那么我们利用熵权法就给这个指标设的权重也几乎为0（即在做综合评价时，一个学生违规与否对他三好学生的评奖没有啥影响的），但是一般情况下，一个学生如果违规了，大概率是评不上三好学生的，也就是说违规这个指标起到了较强的决定性，它的指标权重应该是较大的。

原理及步骤

假设有n个要评价的对象，m个评价指标，先构造成n行m列的矩阵。

1. 正向化（n行m列）

   效益性指标、成本型指标、区间型指标

2. 标准化

   利用向量规范法标准化

3. 确定概率的计算，可能是个虚构出来的概率。

4. 根据公式计算信息熵，归一化得到熵权

TOPSIS（理想解法）

原理

多属性决策当中一种有效的多指标评价方法，通过构造评价问题的正理想解和负理想解，即个指标的最优解和最劣解，通过计算各个方案到理想方案的相对贴近度，来对方案进行排序，从而选出最优的方案。

步骤

1. 由于TOPSIS法采用的是欧几里得距离，我们应该采用向量规范法来对数据进行预处理。
2. 并利用熵权法确定指标的权重，构造加权规范矩阵。
3. 确定正负理想解
4. 计算各方案到正负理想解的距离（欧几里得距离）
5. 对方案按得分值（排序指标值）进行排序
6. 选出最优方案

模糊综合评价

主要用于人才资源的考核评价。

一级模糊综合评价模型的建立

1. 确定因素集，即指标集。
2. 确定评语集，即指标的属性值（评价值），如好-较好-中等-较差-很差等
3. 确定指标权重，加权平均法，众人评估法
4. 构造模糊综合判断矩阵
5. 综合评判

多层次模糊综合评判

1. 按照离散数学中等价类的思想，将因素集（指标集）按某种属性分成多个子集，如果包含嵌套的话，就是即将指标集分成了一级指标、二级指标、三级指标等等。
2. 确定一级指标到多级指标的权重
3. 对每一个因素集分别做出综合评判，对一级指标到二级指标就构造对应的一级综合评判，得到一级评判向量，对二级指标到三级指标就构造对应的二级综合评判，得到二级评判向量。
4. 找到数值最大的分值对应的等级，即为该员工的评价结果
5. 以此类推评价出其它员工的成绩。

灰色关联分析

1. 确定比较对象
2. 确定各指标对应的权重
3. 计算灰色关联系数
4. 计算灰色加权关联度
5. 评价分析

数据包络法（DEA）

评价具有多指标输入和多指标输出系统的较为有效的方法。

主要用代码实现。

主成分分析法

1. 对原始数据进行标准化处理
2. 计算相关系数矩阵
3. 计算特征值和特征向量选择p个主成分，计算综合评价值

用于聚类降维

用于回归分析消除多重共线性

秩和比估计法

秩和比是行（或列）秩次的平均值，是一个非参数统计量，具有0-1连续变量的特征。

1. 编秩
2. 计算秩和比
3. 计算概率单位
4. 计算直线回归方程
5. 分档排序

人工神经网络评价法

待补充