聚类分析、matlab\我国各地区普通高等教育发展状况分析、Q型、R型聚类

• 聚类分析又称为群分析，是对多个样本（或指标）进行定量分类的一种多元统计分析方法。对样本进行分类称为Q型聚类分析，对指标进行分类称为R型聚类分析。
• 本文讲解层次聚类（谱系聚类）

Q型聚类分析

样本的相似性度量

1. 闵氏(Minkowski)距离

$$d_q(x,y)=[\sum _{k=1}^p|x_k-y_k{|}^q{]}^{\frac{1}{q}}$$

1. $q=1$，绝对值距离

$$d_1(x,y)=\sum _{k=1}^p|x_k-y_k|$$

2. $q=2$，欧几里得距离

$$d_2(x,y)=[\sum _{k=1}^p|x_k-y_k{|}^2{]}^{\frac{1}{2}}$$

3. $q=\infty$，切比雪夫距离

$$d_{\infty }(x,y)=\underset{1\le k\le p}{\max }|x_k-y_k|$$

2. 马氏(Mahalanobis)距离

$$d(x,y)=\sqrt{(x-y{)}^T{\Sigma }^{-1}(x-y)}$$
$x$,$y$来自$p$维总体$Z$的样本观测值；$\Sigma$为$Z$的协方差矩阵，实际中$\Sigma$往往是位置的，常常需要用样本协方差矩阵来估计。

3. 此外还有样本相关系数、夹角余弦和其它关联性度量作为相似性度量

类与类间的相似性度量

1. 最短距离法

$$D(G_1,G_2)=\underset{\begin{array}{c}{x}_i\in G_1\\ y_j\in G_2\end{array}}{\min }\{d(x_i,y_j)\}$$

2. 最长距离法

$$D(G_1,G_2)=\underset{\begin{array}{c}{x}_i\in G_1\\ y_j\in G_2\end{array}}{\max }\{d(x_i,y_j)\}$$

3. 重心法

$$D(G_1,G_2)=d(\bar{x},\bar{y})$$
$\bar{x}$，$\bar{y}$分别为$G_1$，$G_2$的重心。

4. 类平均法

$$D(G_1,G_2)=\frac{1}{n_1{n}_2}\sum _{{}_i\in G_1}\sum _{y_j\in G_2}d(x_i,y_j)$$

5. 离差平方和法（Ward法）

$$D_1=\sum _{x_i\in G_1}(x_i-\bar{x}{)}^T(x_i-\bar{x})$$
$$D_2=\sum _{y_j\in G_2}(y_j-\bar{y}{)}^T(y_j-\bar{y})$$
$$D_{12}=\sum _{z_k\in G_1\cup G_2}(z_k-\bar{z}{)}^T(z_k-\bar{z})$$
$\bar{x}$，$\bar{y}$，$\bar{z}$分别为$G_1$，$G_2$和$G_1\cup G_2$的重心。
$$D(G_1,G_2)=D_{12}-D_1-D_2$$

系统(层次)聚类流程

1. 将每个对象看成一类，计算两两之间的距离（距离矩阵）
2. 将距离最小的两个类合并成新类
3. 重新计算新类与所有类之间的距离
4. 重复2 3步，知道所有类最后合并成一类

R型聚类分析

• 按照变量的相似关系把它们聚合成若干类，进而找出影响系统的主要因素

变量相似性度量

1. 相关系数：用变量$x_j$($x_{1j},x_{2j},...,x_{nj}$)与$x_k$的样本相关系数$r_{jk}$作为它们的相似性度量

$$r_{jk}=\frac{{\sum }_{i=1}^n(x_{ij}-\overline{x_j})(x_{ik}-\overline{x_k})}{[{\sum }_{i=1}^n(x_{ij}-\overline{x_j}{)}^2{\sum }_{i=1}^n(x_{ik}-\overline{x_k}{)}^2{]}^{\frac{1}{2}}}$$

2. 夹角余弦：

$$r_{jk}=\frac{{\sum }_{i=1}^n{x}_{ij}{x}_{ik}}{({\sum }_{i=1}^n{x}_{ij}^2{\sum }_{i=1}^n{x}_{ik}^2{)}^{\frac{1}{2}}}$$

两类变量的距离

1. 最长距离法

$$R(G_1,G_2)=\underset{\begin{array}{c}{x}_j\in G_1\\ x_k\in G_2\end{array}}{\max }\{d_{jk}\}$$
$d_{jk}=1-|r_{jk}|$或$d_{jk}^2=1-|r_{jk}{|}^2$

变量聚类

• 变量聚类和层次聚类思路和过程是一样的

聚类分析案例——我国各地区普通高等教育发展状况分析

$x_1$为每百万人口高等院校数； $x_2$为 每十万人口高等院校毕业生数； $x_3$为每十万人口高等院校招生数； $x_4$为每十万人口高 等院校在校生数；$x_5$为每十万人口高等院校教职工数；$x_6$为每十万人口高等院校专职 教师数；$x_7$ 为高级职称占专职教师的比例；$x_8$ 为平均每所高等院校的在校生数； $x_9$为 国家财政预算内普通高教经费占国内生产总值的比重；$x_{10}$ 为生均教育经费 。
部分数据如下表所示：

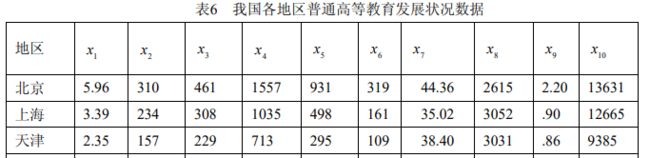
先对变量进行聚类选出指标，再对样本进行聚类。

clc;clear
a=load('gj.txt');
b=zscore(a); %数据标准化

%% R型聚类
r=corrcoef(b);%计算相关系数
d=tril(1-abs(r));%根据相关系数计算距离，并取矩阵的下三角部分
d=nonzeros(d)'; %取出非零数据形成一个向量

%或者直接使用这种方法求距离向量
%d=pdist(b','correlation'); %b需要转置是因为在R型聚类中，b的每一列是一个样本，而pdist需要的是每一行是一个样本
z=linkage(d,'average');%按类平均法聚类
figure()
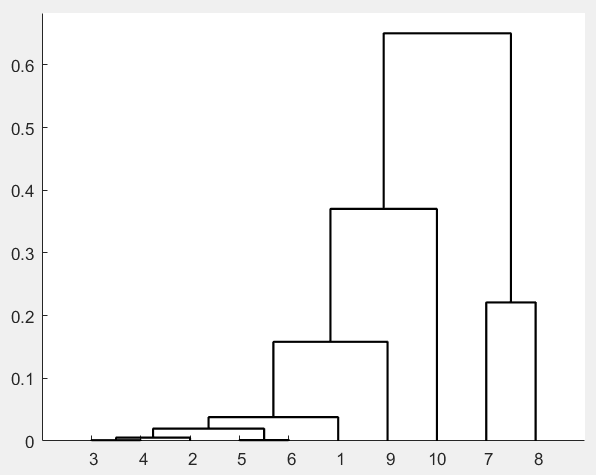
h=dendrogram(z);
set(h,'Color','k','LineWidth',1.3)
T=cluster(z,'maxclust',6);

%可以将求距离pdist，聚类过程linkage，聚类结果cluster 合并为一个函数
%hidx=clusterdata(data,'maxclust',numClust,'distance',dist_h,'linkage',link);
%T=clusterdata(b','maxclust',6,'distance','correlation','linkage','average');

for i=1:6
  tm=find(T==i);  %求第i类的对象
  tm=reshape(tm,1,length(tm)); %变成行向量
  fprintf('第%d类的有%s\n',i,int2str(tm)); %显示分类结果
end
%根据聚类结果选择2(在第2类中，2是最后被聚类的) 1 9 7 8 10六个指标

%% Q型聚类
%根据这6个指标对30个地区进行聚类
b_=b(:,[1:2,7:10]);
y=pdist(b_);%求对象间的欧式距离（默认）,y的结果是行向量，squareform(y)可转成距离矩阵
z=linkage(y,'average');
figure()
h=dendrogram(z);
set(h,'Color','k','LineWidth',1.3)

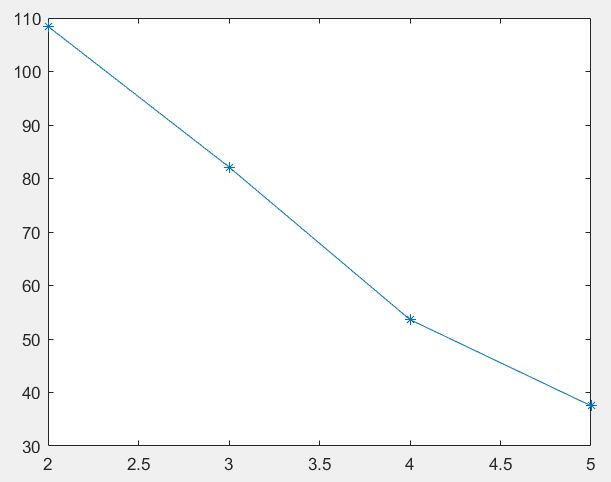
%% 用sse画肘部图
sse=[];
for k=2:5
  T=cluster(z,'maxclust',k);
  s=zeros(1,k);
  for i=1:k
    tm = find(T==i);%第i类有哪些地区
    mean_=mean(b_(tm,:),1);
    for j=1:length(tm)
      s(i)=s(i)+sum((b_(tm(j),:)-mean_).^2);
    end
   end
  sse=[sse,sum(s)];
%fprintf('分为%d类时的sse=%f\n',k,sum(s));
end
figure()
plot(2:5,sse,'*-')

% 设分为K个类别
K=4;
for i=1:K
  tm=find(T==i);  %求第i类的对象
  tm=reshape(tm,1,length(tm)); %变成行向量
  fprintf('第%d类的有%s\n',i,int2str(tm)); %显示分类结果
end