神经网络学习（一）：拟合简单函数

前言

学习用神经网络做点数学上的研究，刚开始摸索，记录一下过程。

今天是用深度学习（Deep Learning）来拟合一些函数（因为多项式的拟合比较简单，直接学习参数就可以了所以就没有必要放出来了），准备设计一个简单神经网络来拟合函数

训练流程

1.定义网络

        选择自定义一个简单神经网络，大部分都直接继承父类就行了，其中fc1是输入数据映射到神经网络隐藏层，fc2是隐藏层给出到输出层的数据。

        前向传播中我加入了激活函数act，目的是为了更好地映射（其实是实验发现不加误差就是nan），经过试验发现使用tanh（）的效果是最好的，其他可参考的激活函数有Sigmoid()，Relu（）两种。

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.fc1 = nn.Linear(1,64)
        self.fc2 = nn.Linear(64,1)
    def forward(self, x):
        o = self.fc1(x)
        o = self.act(o)
        out = self.fc2(o)
        return out
    def act(self, x):
        return torch.tanh(x)

2. 定义损失

        损失可以自己写，也可以调用现有的损失函数计算方法，下面使用的就是2-范数来计算损失

loss_fn = nn.MSELoss(reduction='mean')

        这里的参数reduction可以是'mean'，也可以是'sum'，当然也可以是'none'，取决于你的目的具体可以参考pytorch的nn.MSELoss损失函数 - Picassooo - 博客园MSE是mean squared error的缩写，即平均平方误差，简称均方误差。 MSE是逐元素计算的，计算公式为： 旧版的nn.MSELoss()函数有reduce、size_average两个参https://www.cnblogs.com/picassooo/p/13591663.html

3.选择优化器

optimizer = optim.SGD(net.parameters(),lr= lr)

4.训练&可视化（main）

为了能够更好地看网络学的咋样了，我在循环里加入了图像显示

if __name__ == "__main__":
    x = torch.linspace(0, 10, 2000)
    x_T = x.view(2000, 1)
    y = torch.exp(x)
    y_T = y.view(2000, 1)
    net = Net()
    lr = 1e-4
    loss_fn = nn.MSELoss()
    optimizer = optim.SGD(net.parameters(),lr= lr)
    # 开启图像互动模式
    plt.ion()
    for i in range(10 ** 5):
        optimizer.zero_grad()
        y_train = net(x_T)
        loss = loss_fn(y_train,y_T)
        if i % 10000 == 0:
            plt.cla()
            plt.scatter(x.detach().numpy(),y.detach().numpy())
            plt.plot(x.detach().numpy(), y_train.detach().numpy(), c='red',lw=5)
            plt.text(0.5, 0, 'Loss=%.4f' % loss.item(), fontdict={'size': 20, 'color': 'red'})
            print(f'times {i} - lr {lr} -  loss: {loss.item()}')
            plt.pause(0.1)
        loss.backward()
        optimizer.step()
    plt.ioff()
    plt.show()
    y2 = net(x_T)
    plt.plot(x.detach().numpy(), y.detach().numpy(), c='red', label='True')
    plt.plot(x.detach().numpy(), y2.detach().numpy(), c='blue', label='Pred')
    plt.legend(loc='best')

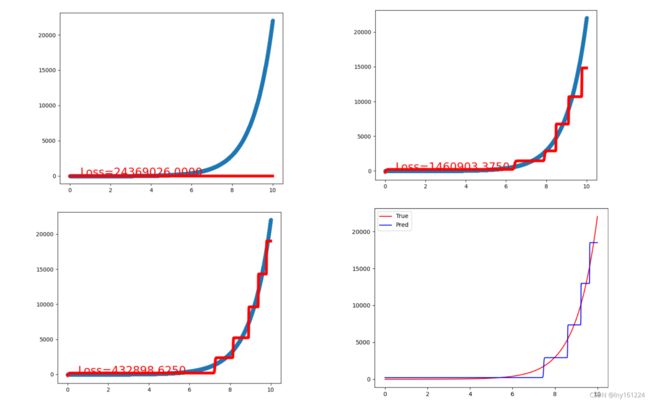
    plt.show()

训练结果

        可以看到训练过程是一步一步在爬升，这应该是SGD的原因（我记得我试了其他优化器，效果不咋地就换回来了）

总结与期望

        利用深度学习来做模拟，不需要考虑原本的参数怎么设置，也不需要考虑怎么去优化，这些都交给神经层，交给优化器。只要确定了损失函数，只需要正向传播得到损失Loss，然后对损失反向传播loss.backward()，然后让优化器optimizer.step()更新参数就可以了。如此一来，只要你有输入和样本输出，都可以用模型去训练，可以根据难度调整网络结构（调整隐藏层和激活函数）

        接下来准备对微分方程进行模拟，在给定了微分方程和初值条件之后，进行模拟函数。与本文的不同点就是损失计算，不能够直接知道当x等于某个值的时候y对应值，那么就没办法去拟合曲线，所以想到用整个函数作为损失，根据PINN的思想

        其中MSE是损失，是初值条件带来的损失，是函数带来的损失，使他们俩的结果为损失Loss,对其反向传播从而进行训练网络

源代码

"""
神经网络拟合函数exp(x)
"""
import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
import torch.optim as optim
class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.fc1 = nn.Linear(1,64)
        self.fc2 = nn.Linear(64,1)
    def forward(self, x):
        o = self.fc1(x)
        o = self.act(o)
        out = self.fc2(o)
        return out
    def act(self, x):
        return torch.tanh(x)
if __name__ == "__main__":
    x = torch.linspace(0, 10, 2000)
    x_T = x.view(2000, 1)
    y = torch.exp(x)
    y_T = y.view(2000, 1)
    net = Net()
    lr = 1e-4
    loss_fn = nn.MSELoss()
    optimizer = optim.SGD(net.parameters(),lr= lr)
    # 开启图像互动模式
    plt.ion()
    for i in range(10 ** 5):
        optimizer.zero_grad()
        y_train = net(x_T)
        loss = loss_fn(y_train,y_T)
        if i % 10000 == 0:
            plt.cla()
            plt.scatter(x.detach().numpy(),y.detach().numpy())
            plt.plot(x.detach().numpy(), y_train.detach().numpy(), c='red',lw=5)
            plt.text(0.5, 0, 'Loss=%.4f' % loss.item(), fontdict={'size': 20, 'color': 'red'})
            print(f'times {i} - lr {lr} -  loss: {loss.item()}')
            plt.pause(0.1)
        loss.backward()
        optimizer.step()
    plt.ioff()
    plt.show()
    y2 = net(x_T)
    plt.plot(x.detach().numpy(), y.detach().numpy(), c='red', label='True')
    plt.plot(x.detach().numpy(), y2.detach().numpy(), c='blue', label='Pred')
    plt.legend(loc='best')

    plt.show()