浅谈算法分析
浅谈算法分析
- 算法的时间复杂程度分析
-
- 计算原子操作
- 随输入变化进行测量操作
- 最坏情况输入研究
- 七种常见函数
-
- 常数函数
- 线性函数
- 二次函数
- 对数函数
- nlogn函数
- 三次函数
- 指数函数
- O符号
- Ω符号
- Θ符号
程序设计的初衷是找到更为优秀的解决问题的算法,所谓优秀,会体现在两个方面,即对空间和时间的耗费量。一个好的算法,对时间和空间的需求量是更少的,有些时候算法对空间和时间的消耗不能同步降低,此时我们的算法会选择消耗更多空间换取执行时间的减少。
算法的时间复杂程度分析
由于对算法的空间的分析比较简单,并且很多情况下我们的空间余量是非常足够的,因此我们更关注的是如何减少算法的时间复杂程度。对于一段代码,我们可以设计一系列的输入,通过加入时间函数的方法看看算法实现目的所需要的具体时间,这种方法就是实验研究。比如,我们设计一个选择排序:
from time import time
start_time=time() # 标记起始时间
def SelecionSort(series=[]): # 升序选择排序
for i in range(len(series)):
for j in range(i, len(series)): # 将最小值提到当前的最前位置
if series[i] > series[j]:
series[i], series[j] = series[j], series[i]
return series
SelecionSort(series=[9,8,7,4,5,2,3,10,1,12,0,6,11]*20)
# 把列表设置长一些,避免运行时间过短
# 在此没有选择输出,小伙伴们可以自己尝试打印下
end_time=time() # 标记截止时间
elapsed=end_time-start_time
print(elapsed)
# 输出为:0.0019888877868652344
在此我们就能得到一个代码的运行时间。但是这种实验分析的方法存在以下的挑战:
- 很难直接对比两个算法的实验运行时间,需要在相同软硬件环境中进行;
- 实验只有在有限的一组测试输入下才能完成,但以选择排序为例,很可能多组等大的测试数据需要移动列表元素的次数不一样从而导致测试误差;
- 为了在实验上执行算法来研究它的执行时间,算法必须完整实现。
因此,我们做算法分析时,使用试验分析的方法并不十分适用。先来了解一些基本概念:
计算原子操作
为了在没有执行实验时分析一个算法的执行时间,我们用一个高层次的算法描述直接进行分析,为此我们可以定义一系列的原子操作:
- 给对象制定一个标识符
- 确定与这个标识符相关联的对象
- 执行算数运算(例如两数相加)
- 比较两个数的大小
- 通过索引访问python列表的一个元素
- 调用函数(不包括执行函数内容)
- 从函数返回
以上就是部分原子操作。从形式上说,原子操作相当于一个低级别指令,期执行时间是常数。理想情况下,这可能是被硬件执行的基本操作类型。我们不需要确定每一个原子操作的具体执行时间,而是简单的计算有多少原子操作被执行,用数字t作为算法执行时间的度量。如果可以假设不同的原子操作的运行时间是非常相似的,那么原子操作数t既可以与真实运行时间形成一个正比的关系,不同的软硬件环境可以影响这个正比关系的比例系数,但不会影响操作次数t。
随输入变化进行测量操作
为了获取一个算法运行时间的增长情况,我们把一个算法和函数f(n)联系起来,其中把执行的原子操作数量描述为输入大小n的函数f(n)。后面我很还会介绍7个最常见的函数。
最坏情况输入研究
前面我们分析了,输入的不同会影响算法的实际执行时间,比如我们传递一个已经是顺序排列的列表,和传递一个逆序排列的列表,选择排序所消耗的理论时间也是有所不同的。我们可以尝试把运行时间表示为所有可能的相同大小数入的平均值函数。不幸的是,这样的平均情况分析也是相当具有挑战性的,他要求定义一组输入的概率分布,这并不是一个容易的工作。不过如果我们按照最坏的情况进行分析,分析结果的包容性会更好,因为如果算法在最坏情况下仍能有较好的表现,那么在其他情况下这种算法的表现依然不会差。并且分析起来也更加简单。因此,此后的内容中,如无特别指明,我们都按最坏的情况把算法的运行时间表示为输入大小n的函数。
七种常见函数
常数函数
常数函数即无论输入n如何,运行的结果都是固定的常数值,表达为:
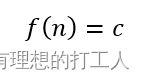
换言之,我们的输入大小n对代码的执行并没有影响,f(n)的值都为c。由于我们对整数函数最感兴趣,因此最基本的常数函数我们将其定义为g(n)=1,也即f(n)=cg(n)。
常数函数描述的是在计算机上需要做的基本操作的步数,也就是通常被用来描述计算机原子操作的个数。比如,在之前的选择排序例子中,返回操作所耗费的时间和输入完全无关,输入为何值,返回操作只需要做一次,因此我们可以把它看做一个常数函数。
线性函数
另一个简单却很重要的函数是线性函数。线性函数的表达为:
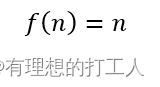
即给定输入的大小直接正比于函数运行的时间。举一个比较直观的例子,我们用一个数字与长度为n的列表中每一个元素的大小都比较一下,所花费的时间便是一个简单的线性函数。
二次函数
二次函数也是一个简单但常见的函数。其表达为:
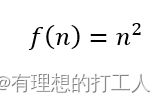
我们仍以选择排序的代码为例,可以看到这部分内容为一个循环的嵌套:
for i in range(len(series)):
for j in range(i, len(series)):
if series[i] > series[j]:
series[i], series[j] = series[j], series[i]
执行完一次内层循环所需要的时间为n,(n-1),(n-2),…1,0,因此执行完这个嵌套循环所花费的时间即为:

对于这个结果,我们只需要截取最大项作为算法所需时间的估计即可,因为这个结果随着n的增长,n2的增长率是最快的,因此时间复杂程度可以记成n2。这里不懂的小伙伴可以空降到O符号处进行学习。
对数函数
对数函数在算法中经常出现,甚至可以说是无处不在的,常见的对数函数形式为:

其中常数b>1,且通常取2。在b=2时,如果我们通常会省略他的符号:
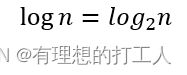
logn的增长率是非常缓慢的,因此时间复杂程度为logn的算法是非常友好的。一个比较典型的例子是二分查找代码:
def find(x,series=[]):
series.sort()
low = 0
high = len(series) - 1
mid = (low + high) // 2
while low<high:
if series[mid]<x:
low = mid
mid = (low + high) // 2 + 1
elif series[mid]>x:
high = mid
mid = (low + high) // 2
else:
return series[mid],mid
return False
series=[i+1 for i in range(20)]
print(find(17,series))
print(find(0,series))
# 输出为:(17, 16)
# False
这个查找算法是每次从标记的low和high位置的中间值mid进行对比,因为列表是顺序排列,所以如果中间值比待查找值大,就从mid到high重新进行下一轮查找,反之就从low到mid部分重新查找。由于每次的(low+high)都(近似)是上一次的一半,因此最差的情况下(如没有查找到的情况)需要查找的次数为logn。
nlogn函数
接下来,我们讨论的函数是nlogn函数:
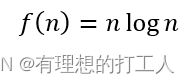
nlogn函数是一个增长率比n快但要小过n2很多的函数,因此,与二次函数比起来,我们更希望一个算法的增长率与nlogn成正比。
三次函数
三次函数类似于二次函数,表达式为:
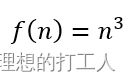
一个简单的三重循环就可能缔造一个三次函数。时间复杂程度为三次函数的算法,由于时间花费随着输入增加的增长速度太快,因此并不是令人满意的算法,然而它确实会时不时地出现。
指数函数
在算法分析中的另一个函数是指数函数:
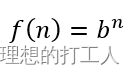
其中,b是一个常数,将其称为底数。指数函数的增长率非常快,甚至在n较大时,其增长率会远远高于三次函数。这样的时间消耗显然是我们很不希望看到的,然而,在一些设计不好的递归算法中,类似时间复杂程度的算法会经常出现。
O符号
我们可以认为O符号是对一个算法所需要耗费时间的渐进估算。下面我们用数学的语言描述一下O符号:
当n≥n0≥1时,若有:
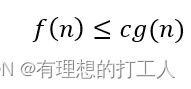
其中c>0,f(n)为算法实际的时间消耗函数,我们就可以说f(n)的时间复杂程度是O(g(n))。
以选择排序为例,由于假设计算机原子操作所需要的时间相同,
def SelecionSort(series=[]): # 升序选择排序
for i in range(len(series)):
for j in range(i, len(series)): # 将最小值提到当前的最前位置
if series[i] > series[j]:
series[i], series[j] = series[j], series[i]
return series
SelecionSort(series)
假如series长度为n,使用这段代码进行选择排序最后花费的时间正比于:

其中,两个1分别来自于函数调用和return语句。然而,当n足够大时,以“抓大放小”的思想来看,整个代码的时间消耗主要取决于n2/2部分,而n2/2的增长率又可以用n2近似概括,所以我们可以说,该算法在输入量很大的情况下,消耗的时间近似于与输入量的平方成正比。用符号表示,即可表述为选择排序的时间复杂程度为O(n2)。
Ω符号
上面提到,O代表着用g(n)函数近似表达f(n)函数,这两个函数结果和增长率之间的关系均为f(n)≤cg(n)。Ω符号则给我们提供了另一种渐进表达:
当n≥n0≥1时,若有:

我们说f(n)是Ω(g(n))。
Θ符号
Θ符号代表的含义是如果f(n)即可以表示成O(g(n)),又可以表示为Ω(g(n)),即:
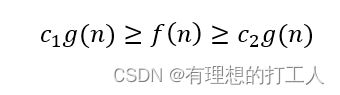
则可以说f(n)是Θ(g(n)),例如:

因此可以说f(n)是Θ(n2)。
虽然我们介绍了三种符号,但算法分析中最主要最常用的符号为O。因为它最贴合我们“分析最坏情况下的时间复杂程度”的需求。
本节我们介绍了一些算法分析的基本理论,以及一些常见的函数。从下一节开始,我们将正式进入对算法的讨论。有时间的小伙伴们可以适当学习获回顾一下常见函数的运算规则。下节见~