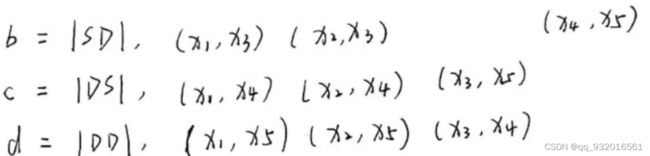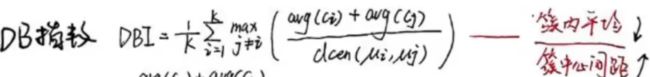机器学习算法----聚类 (K-Means、LVQ、GMM、DBSCAN、AGNES) (学习笔记)
文章目录
- 聚类简介
-
- 聚类和分类的区别
- 基础概念
-
- 外部指标
- 内部指标
- 距离度量和非距离度量
-
- 距离度量方法
- 有序属性和无序属性
- 原型聚类
-
- k均值算法(K-means)
- 学习向量化（LVQ）
- 高斯混合聚类（GMM）
- 密度聚类(DBSCAN)
- 层次聚类(AGNES)
- 学习参考
聚类简介
之前学习的决策树、随机森林或者逻辑回归都属于有监督学习，就是有老师在指导他，给了他特征和真实标签lable。
今天的这个聚类算法就是无监督学习，不需要真实标签lable。
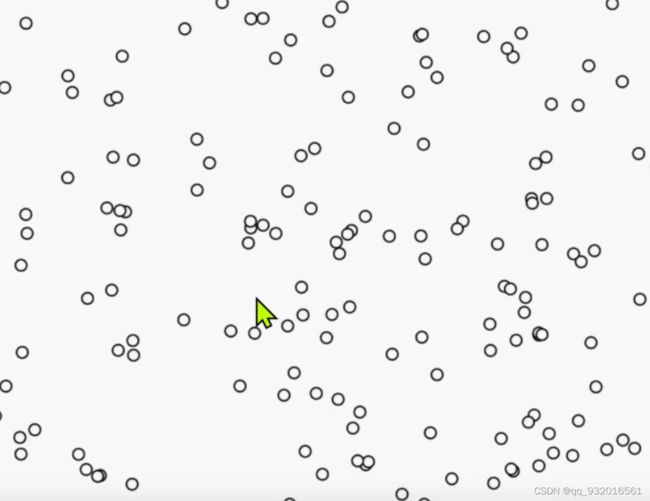
聚类结果:将数据划分成有意义的‘簇’ （类似于集合），簇内样本尽快可能的相同，簇间尽可能的不同。
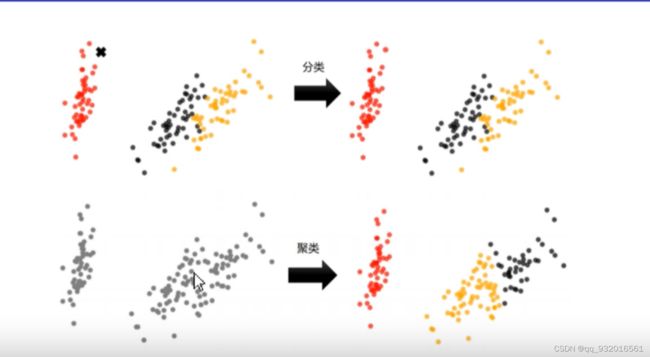
聚类和分类的区别
可以看下面这张图，红色哪里有一个 X 分类是将X分类到三种三色中的一种，而聚类一开始都是灰色，聚类将他们分类，这也看出来了聚类是无监督学习，原始数据没有lable。
基础概念
概念：簇与质心
簇：KMeans将一组N个样本的特征矩阵X划分为K个无交集的簇，在一个簇中的数据就认为是同一类。
质心：簇中所有数据的均值被称为这个簇的质心(centroids)。
外部指标 ： 外界给个标准进行比较.（有监督）
内部指标 ： 没有标准，和自己比.（无监督）
外部指标
用一个例子来看一下各种指标的原理，假设有abcd四个变量，且字母S代表相同，字母D代表不同。
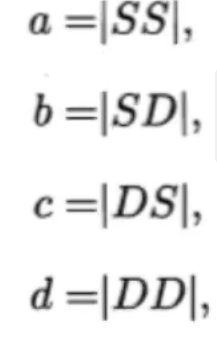
左边是自己分类的，右边是参考(lable)，相当于lable。显然只有 X1和X2是自己分类也在C1，参考(lable)也在C1.
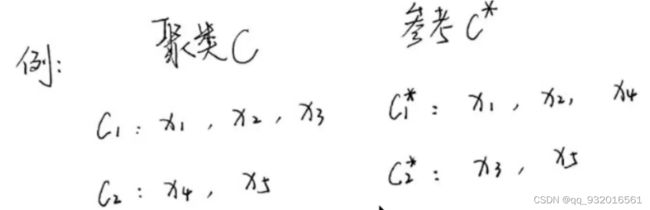
所以 SS 就是 X1 ,X2。
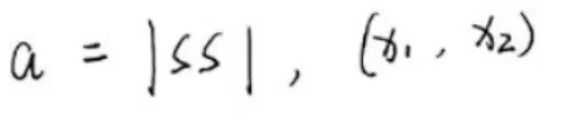
以此类推可以得到其他: x1,x3 一开始同在C1簇 就是S，但参考一个C1一个C2 就是D，所以结果SD。
x1,x2,x3,x4,x5 两两排列组合 一共10种情况。
然后可以计算各种指标，这里带入的值就是 b里有三个集合 所以b就是3。
m是样本数量，本例中 m=5。
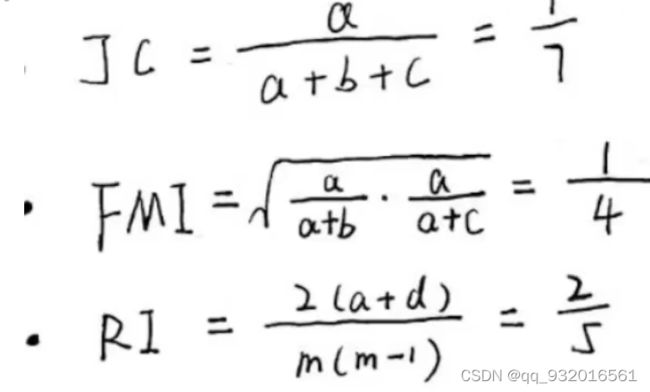
这几个值在 0-1区间，越大越好。
内部指标
同样用一个例子来说明。
avg 簇内样本平均距离。
diam 簇内样本最大距离。
dmin 簇内样本最小距离。
dcen 簇中心距离。
DB指数: 越小越好：
Dunn指数：越大越好
簇间样本最小距离 / 簇内样本最大距离
距离度量和非距离度量
在不断优化聚类的过程中需要有一个距离的计算来判断样本与质心之间的距离。
距离度量满足的性质 ：
非负性 距离大于零
同一性 重叠等于零
对称性，互换相等
直递性 有三个点，类似于两边之和大于第三边。 当k点在i和j点连线上时 等号成立
距离度量方法
样本到质心的距离度量方法 ，x表示其中一个样本点，u表示该簇质心，n表示每个样本点中的特征数目，i表示组成点的每个特征。
曼哈顿距离 与 欧几里得距离 同属于闵氏距离的特例（p=1为曼哈顿距离；p=2为欧氏距离）
采用欧几里得距离，则一个簇中所有样本到质点的距离平方和
其中 ，m为一个簇中的样本个数，j为样本编号。
该公式被称为 簇内平方和(Inertia).
将数据集中所有簇的簇内平方和相加，就得到了整体平方和，(total inertia) 该值越小，表示簇内样本越相似，聚类效果越好。
虽然像KNN 决策树等这类算法中没有损失函数，但Inertia的功能却类似于损失函数。
Sklearn中只能使用欧氏距离。
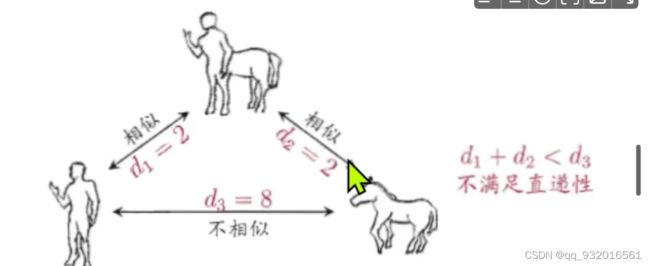
非距离度量的例子：
不符合 直递性 两边之和不大于第三边。
有序属性和无序属性
有序属性：
欧氏距离与曼哈顿距离：
下图中 中间的绿线就是欧氏距离， 黄色 红色 蓝色 就是曼哈顿距离 这三个距离相等。
切比雪夫距离
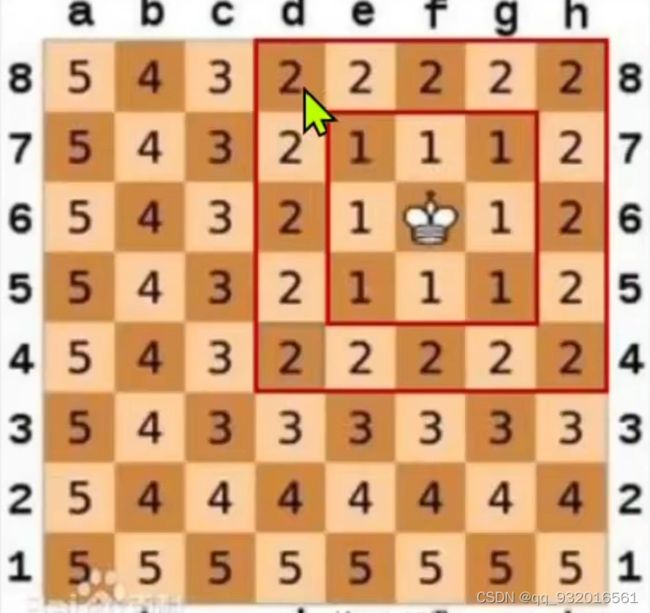
国际象棋，中间的那个棋子，每一圈是1个距离。 可能是横纵坐标取移动的最大值。
无序属性
无序属性计算距离 VDM距离。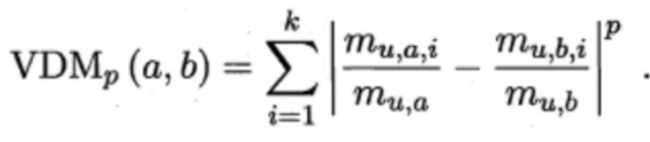
混合距离: 有序和无序相加 闵可夫斯基距离 和 VDM距离相加。
加权距离: 按照属性重要性不同加权
原型聚类
先对原型初始化，然后迭代更新。
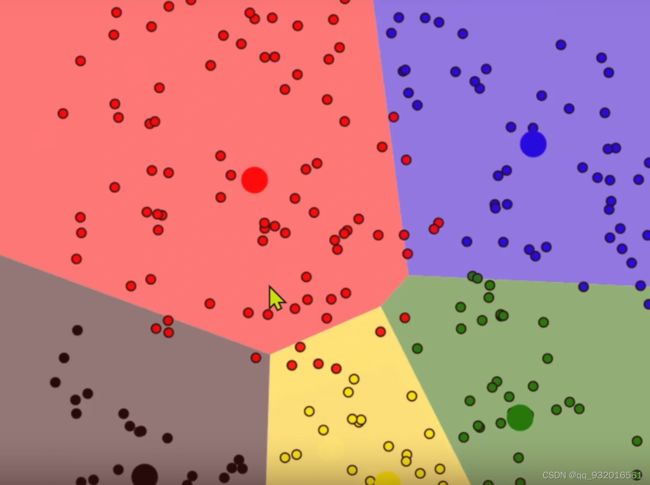
k均值算法(K-means)
- 一开始一堆的样本点。
- 初始化分为不同的簇，然后不断的迭代最后收敛。
更形象的:
1.蓝点就是样本点，红点就是随机生成的簇的中心点。
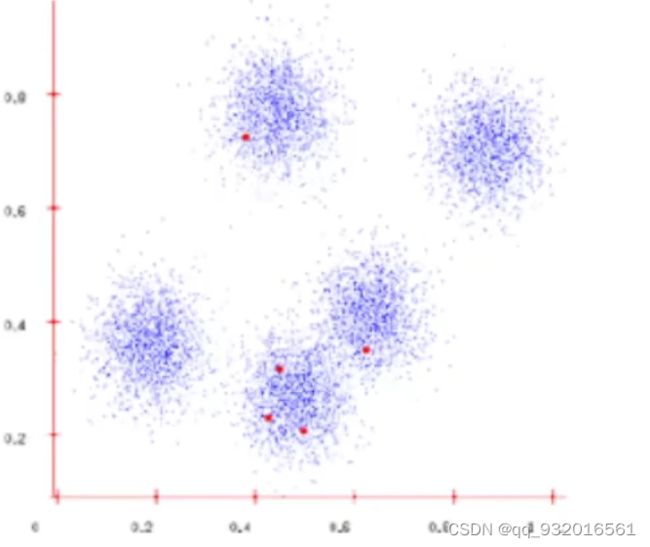
2.分别计算每个样本点到簇的中心点的距离，将他们分成不同的簇(那个点距离近就属于那个簇)。
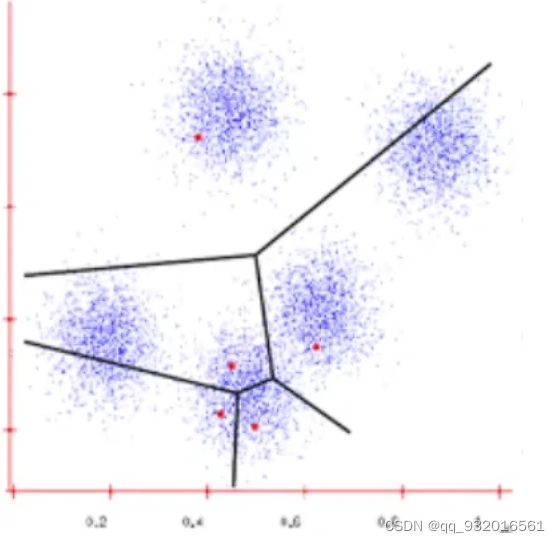
3. 之后暂且忽略红点，然后重新计算每个簇区域的中心点。
新计算的中心点就是绿点。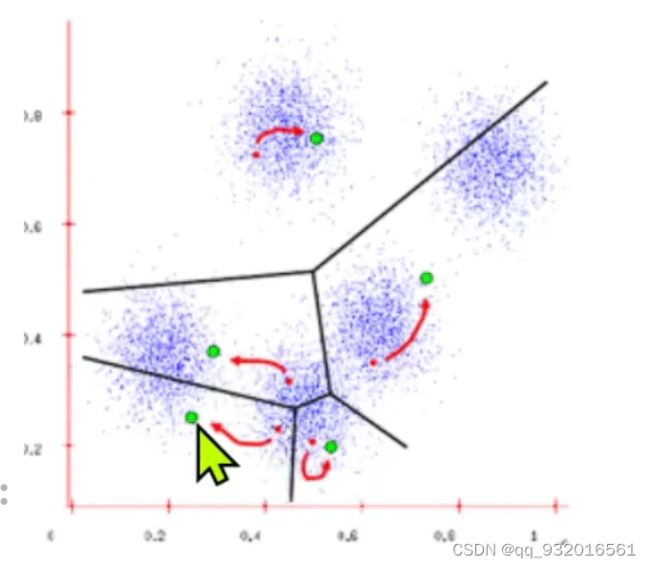
绿色作为新的簇的中心点，继续重新计算每个样本距离中心点的位置，继续重新划分簇的区域。不断迭代直到收敛。
学习向量化（LVQ）
每个样例有类别标签，是有监督学习
结果输出不会给簇的划分，而是给每个类别的原型向量(即中心点)
步骤:
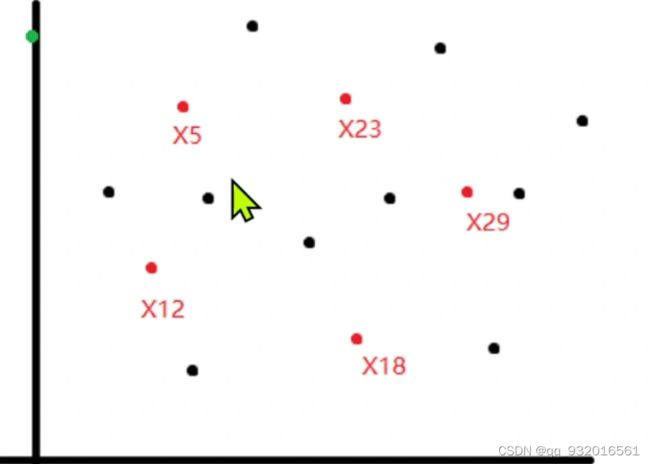
假设一开始都是黑点，然后也是随机选了几个点作为簇中心点(红点)。
开始分析每一个点输入那个簇。显然此时x1点输入p5簇。
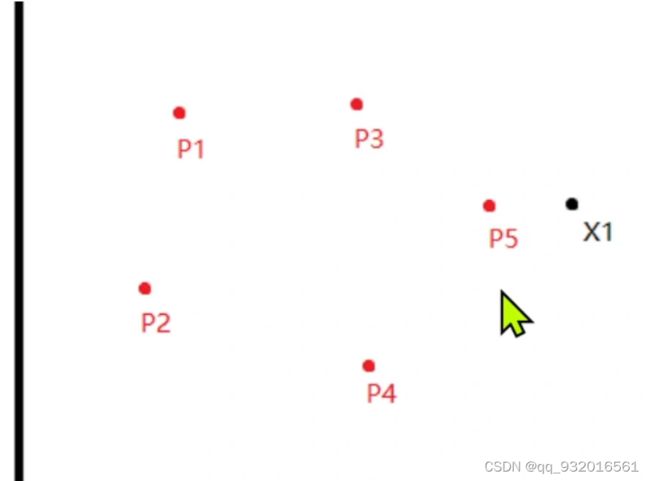
因为这个是有监督的学习，假设 X1和p5是同类别，则p5就靠近一点x1。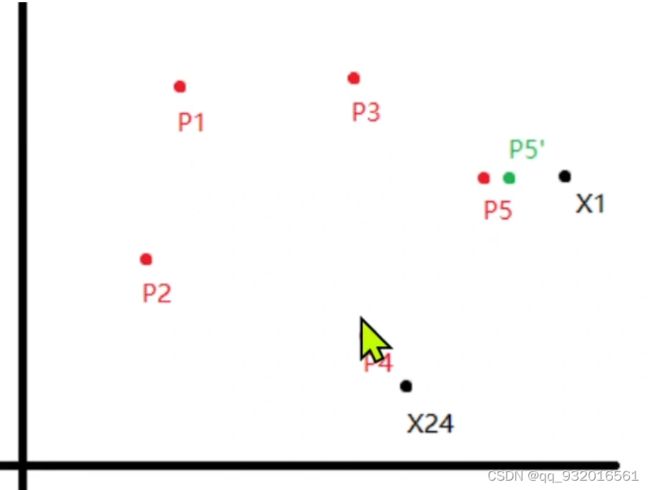
同样 如果现在看x24 ，其属于p4的簇，如果 他俩是不同的类别。则p4就远离x24.
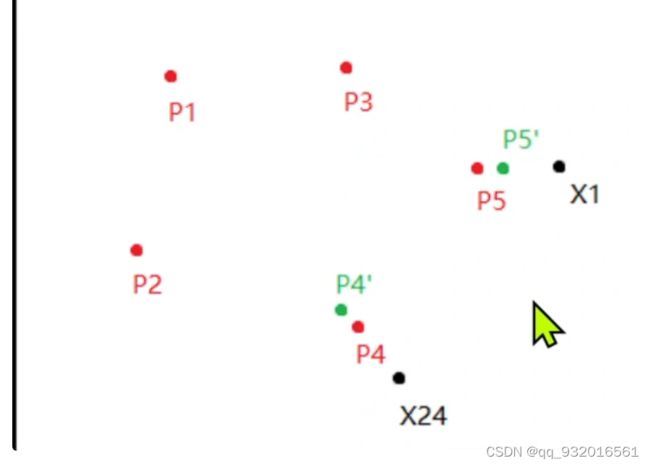
最后输出的是这五个中心点，其中红线就是两点之间的垂直平分线。
高斯混合聚类（GMM）
这里的k就是几个高斯分布，或者说像分成几个簇。
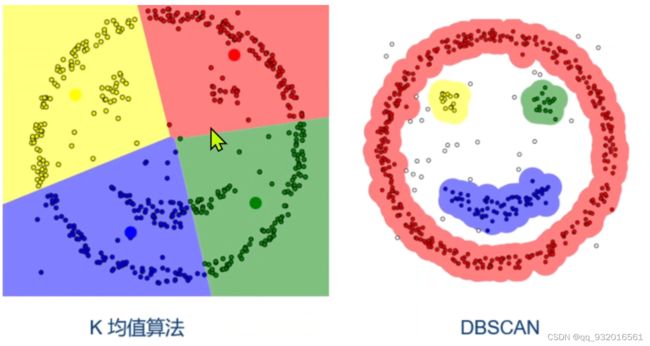
密度聚类(DBSCAN)
通过样本分布的紧密程度确定簇，不断迭代。
由密度可达关系导出最大密度相连的样本集合（聚类）。这样的一个集合中有一个或多个核心对象，如果只有一个核心对象，则簇中其他非核心对象都在这个核心对象的ε邻域内；如果是多个核心对象，那么任意一个核心对象的ε邻域内一定包含另一个核心对象（否则无法密度可达）。这些核心对象以及包含在它ε邻域内的所有样本构成一个类。
对比:
DBSCAN使用一组关于“邻域”概念的参数来描述样本分布的紧密程度，将具有足够密度的区域划分成簇，且能在有噪声的条件下发现任意形状的簇。
一些概念:
邻域：对于任意给定样本x和距离ε，x的ε邻域是指到x距离不超过ε的样本的集合；
核心对象：若样本x的ε邻域内至少包含minPts个样本，则x是一个核心对象；
密度直达：若样本b在a的ε邻域内，且a是核心对象，则称样本b由样本x密度直达；
密度可达：对于样本a，b，如果存在样例p1,p2,…,pn,其中，p1=a,pn=b,且序列中每一个样本都与它的前一个样本密度直达，则称样本a与b密度可达；
密度相连：对于样本a和b，若存在样本k使得a与k密度可达，且k与b密度可达，则a与b密度相连。
层次聚类(AGNES)
在不同层次对数据集进行划分，从而形成树状的聚类结构。
凝聚的层次聚类：一种自底向上的策略，首先将每个对象作为一个簇，然后合并这些原子簇为越来越大的簇，直到某个终结条件被满足。
分裂的层次聚类：采用自顶向下的策略，它首先将所有对象置于一个簇中，然后逐渐细分为越来越小的簇，直到达到了某个终结条件。
自底向上是主要的。
cluster R和cluster S之间的距离计算方法:
1）最小连接距离法（Single Linkage）
取两个簇中距离最近的两个样本的距离作为这两个簇的距离。
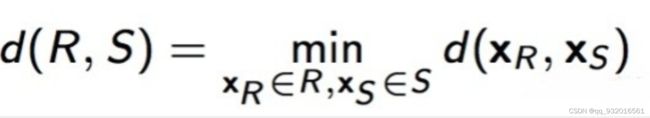
（2）最大连接距离发（Complete Linkage）
取两个簇中距离最远的两个点的距离作为这两个簇的距离。
（3）平均连接距离法（Average Linkage）
把两个簇中的点的两两的距离全部放在一起求均值，取得的结果也相对合适一点。
学习参考
https://zhuanlan.zhihu.com/p/367956614
https://www.bilibili.com/video/BV1fi4y1K7Ke?p=5
https://www.cnblogs.com/pinard/p/6208966.html
https://www.bilibili.com/video/BV12g4y1i7Ad?spm_id_from=333.999.0.0
https://blog.csdn.net/AI_BigData_wh/article/details/78073444