基于PID算法（python）的飞控设计学习日志（一）

PID算法基础

      首先我们需要去了解PID算法的数学原理，数学原理部分借鉴于 @确定有穷自动机 的博客——一文读懂PID控制算法（抛弃公式，从原理上真正理解PID控制）

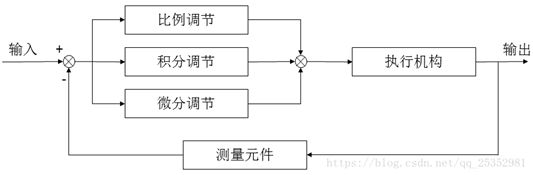
      总的来说，当得到系统的输出后，将输出经过比例，积分，微分3种运算方式，叠加到输入中，从而控制系统的行为。

比例控制算法

u=kp*error  

其中kp表示比例系数，error表示与目标值的误差

但这里有个稳态误差的问题，在实际情况中各种阻力和消耗都会导致在使用比例控制时还未达到目标值时便处于动态平衡，而导致无法满足需求。

积分控制算法

u=kp*error+ ki∗∫error dt

加入积分控制后，会将前面若干次的误差进行累计，可以很好地消除稳态误差，具体效果将会在代码实现的效果图中进行分析解释。

微分控制算法

u=kd*（error（t）-error（t-1））

在离散的情况下，计算t-1时刻和t时刻误差值的差值，如果放在小球摆动模型中则可以看做控制加速度的部分，如果距离目标值较远，则以更快的速度靠近

最终公式将有以上三个部分组成：

其中第一项为比例控制算法，第二项为积分控制算法，第三项为微分控制算法

当然也可以写成更简洁的形式，化简过程如下：

 

 

最后一条公式中的Kp，Ki，Kd都是系数，需要我们在实践中进行调参找到最优良的参数来解决我们的实际问题。感谢@确定有穷自动机对以上学习的贡献，原文链接如下：

https://blog.csdn.net/qq_25352981/article/details/81007075

在python环境下的PID算法的简单演示：

除了51单片机等基于c语言的单片机，如今也有不少基于micropython的单片机在市面上有所研究与应用，如openmv，pyboard等，在普遍通过C语言开发的单片机相比，micropython将会继承python的优势拥有更多的类库和第三方包。

源代码如下：

import matplotlib.pyplot as plt


class PID():
    def __init__(self, dt, max, min, Kp, Kd, Ki):
        self.dt = dt  # 循环时长
        self.max = max  # 操作变量最大值
        self.min = min  # 操作变量最小值
        self.Kp = Kp  # 比例增益
        self.Kd = Kd  # 积分增益
        self.Ki = Ki  # 微分增益
        self.integral = 0  # 直到上一次的误差值
        self.pre_error = 0  # 上一次的误差值

    def calculate(self, setPoint, pv):
        # 其中 pv:process value 即过程值，
        error = setPoint - pv  # 误差
        Pout = self.Kp * error  # 比例项
        self.integral += error * self.dt
        Iout = self.Ki * self.integral  # 积分项
        derivative = (error - self.pre_error) / self.dt
        Dout = self.Kd * derivative  # 微分项

        output = Pout + Iout + Dout  # 新的目标值

        if (output > self.max):
            output = self.max
        elif (output < self.min):
            output = self.min

        self.pre_error = error  # 保存本次误差，以供下次计算
        return output


t = range(300)
pid = PID(0.1, 100, -100, 0.1, 0.01, 0.5)
val = 20
z = []
for i in t:
    inc = pid.calculate(0, val)
    print("val:%f inc:%f" % (val, inc))
    z.append(20 - val)
    val += inc
plt.figure(figsize=(8, 6), dpi=80)
plt.plot(t, z, color="blue", linewidth=1.0, linestyle="-")
plt.show()

由我们创建的类可以看出，第4，5，6个PID类实例变量分别为P,I,D三个参数的值，我们可以通过调整三个参数来看出不同参数组合对控制效果的实现：

（其中P为Kp即比例控制系数，I为Ki即积分控制系数，D为Kd即微分控制系数）

1. P=0.1，I=0.01，D=0.5时，如下图所示：

       2.P=0.05，I=0.01，D=0.5时，如下图所示：

与第一张图对比可以发现，当调小P参数是会导致调整时间更长，抖动更多，这是因为比例控制系数的下调会是单个时间间隔内可调范围的减少

通过调参和观察现象可以更好地理解三个参数的实际意义，大家可以自行实验。

除此以外，在CSDN博客中还发现了一文的源代码能很好地用小球运动解释积分控制算法的例程，一下为链接：

https://blog.csdn.net/chengeng_jd/article/details/105393049

由于一定的项目需求，该系列的学习日志主要围绕基于PID的无人机控制，尽可能才去python变成来实现，当然也有可能因为走不通而重新选择c语言编程，本人为大一人工智能专业学生，上文如有问题或疏漏，欢迎指正！

本文为个人学习路线的记录，如有侵权请联系我个人微信：GZE08_myh