图像处理之理想带阻滤波器、巴特沃斯带阻滤波器和高斯带阻滤波器的matlab实现去噪
一、前言
带阻滤波器是用来抑制距离频域中心一定距离的一个圆环区域的频率，可以用来消除一定频率范围的周期噪声。带阻滤波器包括理想带阻滤波器、巴特沃斯带阻滤波器和高斯带阻滤波器。对于大小为M*N的图像，频率点(u,v)与频域中心的距离为D(u,v)，其表达式为：
二、理想带阻滤波器(IBEF)
1、基本定义
理想带阻滤波器的产生公式为：
其中D0为需要阻止的频率点与频率中心的距离，W为带阻滤波器的带宽。
2、matlab实现理想带阻滤波器去除高斯噪声
（1）实现代码：
close all;
clear all;
clc;
I = imread('football.jpg');
I=rgb2gray(I);
subplot(131),imshow(I);
title('原始图像');
I=imnoise(I,'gaussian');%加入高斯白噪声
subplot(132),imshow(I);
title('加入噪声后所得图像');
% 函数fft2()用于计算二维傅立叶变换
% 函数fftshift()是对函数fft2()作傅里叶变换后得到的频谱进行平移,将变换后的图像频谱中心从矩阵的原点移到矩阵的中心
% 作二维傅里叶变换前一定要用函数im2double()把原始图像的数据类型由uint8转化为double类型
% 否则会因为unit8数据类型只能表示0-255的整数而出现数据截断,进而出现错误结果
s=fftshift(fft2(im2double(I)));
[a,b]=size(s);
a0=round(a/2);
b0=round(b/2);
W=30; % 将理想带阻滤波器的带W设置为30
d0=50; % 将理想带阻滤波器的截止频率D0设置为50
for i=1:a %双重for循环计算频率点(i,j)与频域中心的距离D(i,j)=sqrt((i-round(a/2)^2+(j-round(b/2)^2))
for j=1:b
distance=sqrt((i-a0)^2+(j-b0)^2);
if distance<=d0-(W/2) % 根据理想带阻滤波器产生公式分别进行三次if判断
h=1;
end
if (distance>=d0-W/2)&&(distance<=d0+W/2)
h=0;
end
if distance>d0+W/2
h=1;
end
s(i,j)=h*s(i,j);% 频域图像乘以滤波器的系数
end
end
% real函数取元素的实部
s=real(ifft2(ifftshift(s)));% 最后进行二维傅里叶反变换转换为时域图像
subplot(133),imshow(s,[]);
title('理想带阻滤波所得图像');
2、实现效果：
二、巴特沃斯带阻滤波器(BBEF)
1、基本定义
巴特沃斯带阻滤波器产生公式为：
其中D0为需要阻止的频率点与频率中心的距离，W为带阻滤波器的带宽，n为巴特沃斯滤波器的阶数。
2、matlab实现巴特沃斯带阻滤波器去除高斯噪声
（1）实现代码：
close all;
clear all;
clc;
I = imread('football.jpg');
I=rgb2gray(I);
subplot(131),imshow(I);
title('原始图像');
I=imnoise(I,'gaussian');%加入高斯白噪声
subplot(132),imshow(I);
title('加入噪声后所得图像');
% 函数fft2()用于计算二维傅立叶变换
% 函数fftshift()是对函数fft2()作傅里叶变换后得到的频谱进行平移,将变换后的图像频谱中心从矩阵的原点移到矩阵的中心
% 作二维傅里叶变换前一定要用函数im2double()把原始图像的数据类型由uint8转化为double类型
% 否则会因为unit8数据类型只能表示0-255的整数而出现数据截断,进而出现错误结果
s=fftshift(fft2(im2double(I)));
[N1,N2]=size(s);%求二维傅里叶变换后图像大小
n=5; % 将巴特沃斯带阻滤波器的阶数n设置为5
W=30; % 将巴特沃斯带阻滤波器的带宽W设置为30
d0=50; % 将巴特沃斯带阻滤波器的截止频率D0设置为50
n1=round(N1/2);
n2=round(N2/2);
for i=1:N1 %双重for循环计算频率点(i,j)与频域中心的距离D(i,j)=sqrt((i-round(N1/2)^2+(j-round(N2/2)^2))
for j=1:N2
distance=sqrt((i-n1)^2+(j-n2)^2);
if distance==0
h=0;
else
h=1/(1+((distance*W)/(distance*distance-d0*d0))^(2*n));% 根据巴特沃斯带阻滤波器公式为1/(1+[(D(i,j)*W)/(D^2(i,j)-D0^2)]^2n)
end
s(i,j)=h*s(i,j);% 频域图像乘以滤波器的系数
end
end
% real函数取元素的实部
s=real(ifft2(ifftshift(s)));% 最后进行二维傅里叶反变换转换为时域图像
subplot(133),imshow(s,[]);
title('Butterworth带阻滤波图像');
2、实现效果：
四、高斯带阻滤波器(GBEF)
1、基本定义
高斯带阻滤波器产生公式为：
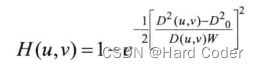
其中D0为需要阻止的频率点与频率中心的距离，W为带阻滤波器的带宽。
2、matlab实现高斯带阻滤波器去除高斯噪声
（1）实现代码：
close all;
clear all;
clc;
I = imread('football.jpg');
I=rgb2gray(I);
subplot(131),imshow(I);
title('原始图像');
I=imnoise(I,'gaussian');%加入高斯白噪声
subplot(132),imshow(I);
title('加入噪声后所得图像');
% 函数fft2()用于计算二维傅立叶变换
% 函数fftshift()是对函数fft2()作傅里叶变换后得到的频谱进行平移,将变换后的图像频谱中心从矩阵的原点移到矩阵的中心
% 作二维傅里叶变换前一定要用函数im2double()把原始图像的数据类型由uint8转化为double类型
% 否则会因为unit8数据类型只能表示0-255的整数而出现数据截断,进而出现错误结果
s=fftshift(fft2(im2double(I)));
[a,b]=size(s);
W=30; % 将高斯带阻滤波器的带宽W设置为30
d0=50; % 将高斯带阻滤波器的截止频率D0设置为50
a0=round(a/2);
b0=round(b/2);
for i=1:a
for j=1:b
distance=sqrt((i-a0)^2+(j-b0)^2); % 根据高斯带阻滤波器公式H(u,v)=1-e^-(1/2)[(D^2(u,v)-D^20)/D(u,v)*W]
h=1-exp(-0.5*((distance^2-d0^2)/(distance*W))^2); % exp表示以e为底的指数函数
s(i,j)=h*s(i,j);% 频域图像乘以滤波器的系数
end
end
s=real(ifft2(ifftshift(s)));% 最后进行二维傅里叶反变换转换为时域图像
subplot(133),imshow(s,[]);
title('高斯带阻滤波图像');
2、实现效果：
由于刚刚开始学习图像处理，对于很多知识理解不到位。如有错误，恳请指正，任重而道远，慢慢加油！