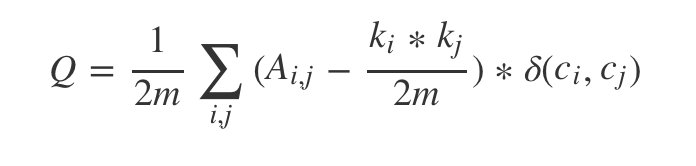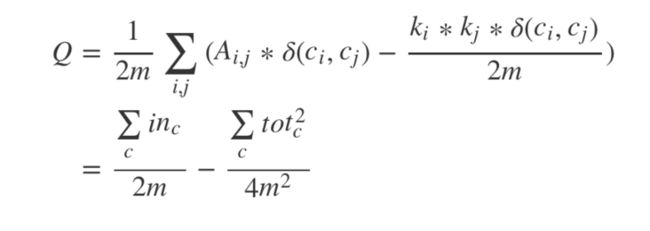Louvain算法在反作弊上的应用

作者 | ANTI

一、概述

随着互联网技术的发展，人们享受互联网带来的红利的同时，也面临着黑产对整个互联网健康发展带来的危害，例如薅羊毛、刷单、刷流量/粉丝、品控、诈骗、快排等等，反作弊作为打击黑产的中坚力量，持续跟黑产对抗着，保证搜索/feed效果的客观公正，保证广告主的合法权益。近年来反作弊算法能力持续提升，黑产很难通过大规模机刷方式获利，已从大规模机刷转向更加隐蔽的小团伙作弊，因此，反作弊进行了团伙作弊挖掘的探索，Louvain就是比较经典的一个算法，下面详细介绍下。

二、Louvain简介

2.1 模块度定义

模块度是对社区划分好坏程度的一种度量，当社区内部的点之间连边越多，社区之间的点连边越少时，模块度越大，表示当前的社区划分情况越好，公式定义如下：

模块度是对社区划分好坏程度的一种度量，当社区内部的点之间连边越多，社区之间的点连边越少时，模块度越大，表示当前的社区划分情况越好，公式定义如下：

其中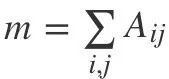表示所有边权和，表示节点 i 和 j 之间的权重，表示与 i 相连的所有边的权重和，表示节点 i所在的社区，表示 x 和 y 是否相同，是的话为 1，否则为 0。

公式并不好直接理解，进行一定的变换可得

其中 c 表示社团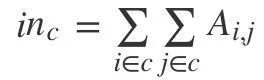，表示社区 c 中所有节点的之间的边权和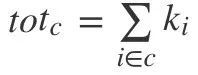，表示社区 c 中所有节点与其他节点的边权和。

模块度前一项描述的是社团内节点之间的边权，该值越大，模块度越大。第二项描述每个社团中所有节点的边权和平方，分母为常量，当所有节点（严格来说是节点的度，即边权）在不同社区中分布越均匀，第二项越小，模块度越大。（第二项重要程度与社团实际的分布情况有关，比如风控场景社团大小分布极不均匀，就会导致第二项结果偏大，模块度偏小，导致模块度的优化目标与实际场景冲突。）

2.2 算法

louvain 以最大化模块度为优化目标，根据模块度公式，整个社区的模块度可以以各个社区为单位计算后求和得到，louvain算法的流程如下：

初始化
将社团中每个节点都看做一个单独的社区。

阶段1：节点合并
遍历所有节点，计算当前节点脱离当前社区，且加入到邻居节点所在社区时，带来的模块度增益，把当前节点移动到增益最大的邻居节点社区中。

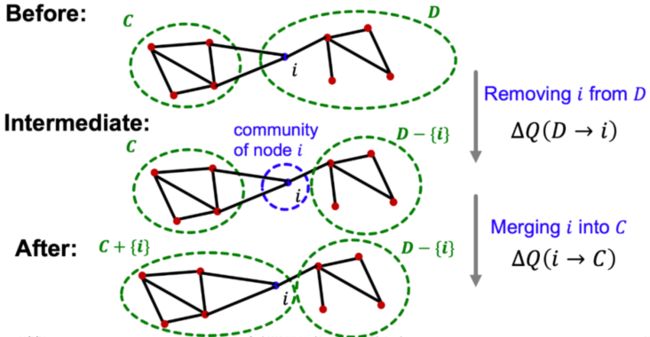
每次计算节点 i 从社团 D 移动到社团 C 中时，根据模块度计算公式可知，此时产生的模块度变化只与当前C、D社区相关，不与其他社区相关，因此计算成本较低，将节点 i 从社区 D 转移到 C 中带来的模块度增益为：

ΔQ\=ΔQ(D→i)+ΔQ(i→C)

直至节点移动不再产生增益，阶段1停止。

阶段2：社区聚合
将同一个社区的多个节点，融合为一个新的节点，社区内节点之前的权重后续不再使用，当前社区与其他社区之间的权重为两个社区所有节点的权重和，从而构建出新的图结构。
回到阶段1不断迭代，直至图结构不再产生改变。

louvain基于贪心算法实现，实际数据中的平均复杂度为 O(nlog(n))，当每一轮迭代中节点数量降低一半时，能达到平均复杂度。

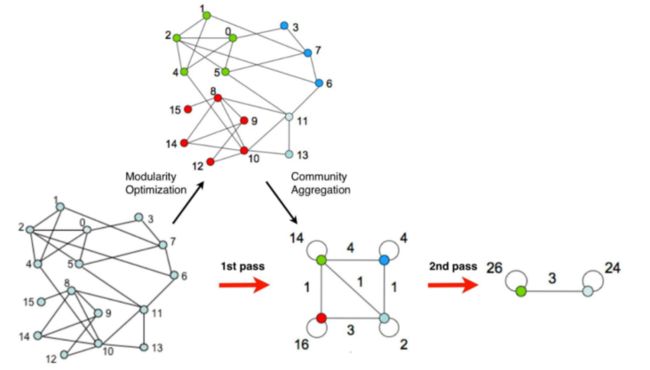
整体流程如下：

三、在反作弊应用

因黑产作弊的收益较大，作弊者就算冒着违法被抓的风险，也有充足的时间和动力与风控团队对抗，在实际业务场景中，过去作弊者最常使用的方式是低成本批量机器作弊被我们严格打击殆尽，目前也只能逐步迁移成了高成本小批量团伙人为作弊，这是黑产攻击方式的演化趋势，也是风控团队技术发展的必要趋势。
我们看一个电商风控的业务场景。少数店铺为了构造虚假的用户体验评分、更优的算法推荐，铤而走险组建团队做起了刷单套利、刷评分等非法操作。而商家获得的非法收益最终却由用户买单。为了还原真实的互联网、给用户带来最优质的体验 ，我们对作弊团伙进行了持续挖掘对抗。
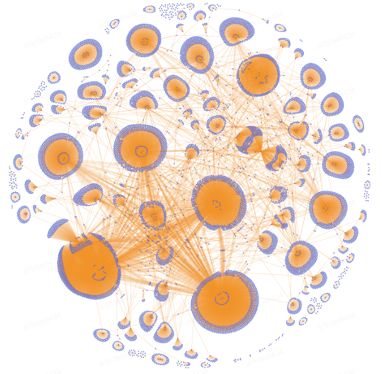
我们基于经典的Louvain算法实现关系网络模型，将作弊数据中错综复杂的关系抽象成数学表达，我们得到层次化的社区发现结果，如下图所示。其中第一张图描述了风险账户的社区发现结果，第二张图描述了交易订单的社区发现结果，精准定位了作弊团伙，拦截作弊订单/交易，增强了风险防控能力，联合公司法务部对多个作弊黑产团伙也进行了数次抓捕。

社区发现示例图一

社区发现示例图二

四、优化

4.1优缺点

优点

1. 平均时间复杂度较低，计算速度相对较快；
2. 支持定义边权 ；
3. 包含层次结构的社团，可以依据社团大小、社团特殊属性来限制最后形成的社团。类似决策树中根据增益、叶子节点数量来限制节点分裂 。

缺点

1. 多轮迭代，不支持流式系统 ；
2. 最差时间复杂度较大，小概率遇到边界数据时，耗时较长；
3. 实际情况中数据分布不均匀时，模块度定义的第二项会产生一定负干扰。

4.2优化思路

模块度的最优求解本身是个 NP 问题，即时间复杂度为 O(M!)，常规数据中无法在短时间内求到最优解。louvain就是利用贪心算法对求解过程做了一定优化，但在 louvain 的基础上，还可以做以下优化：

1. 利用边属性对社团中的边进行关于合并优先级的排序，能取消louvain的多轮迭代，适配流式计算系统。比如边介数：社团中任意两个点的最短路径通过该边的次数；
2. 实际数据中社团分布不均匀时，建议降低模块度中第二项的权重。

---------- END ----------

参考：

[1]原始paper：https://arxiv.org/abs/0803.0476

[2]stanford keynote：http://web.stanford.edu/class...

[3]louvain：https://towardsdatascience.co...

推荐阅读【技术加油站】系列：

百度用户产品流批一体的实时数仓实践

ffplay视频播放原理分析

百度工程师眼中的云原生可观测性追踪技术

使用百度开发者工具 4.0 搭建专属的小程序 IDE

百度工程师教你玩转设计模式（观察者模式）

揭秘百度智能测试在测试自动执行领域实践