【深度学习】吴恩达深度学习-Course2改善深层神经网络:超参数调试、正则化以及优化-第一周深度学习的实用层面编程(下)——梯度检验
视频链接:【中英字幕】吴恩达深度学习课程第二课 — 改善深层神经网络:超参数调试、正则化以及优化
参考链接:
- Gradient Checking
- 【中文】【吴恩达课后编程作业】Course 2 - 改善深层神经网络 - 第一周作业(1&2&3)
资源下载链接(来自参考链接2):
- 本文所用资料
- data.mat下载后名称为9.mat,需要手动更名为data.mat
目录
- 〇、作业目标和作业背景
- 一、所需要使用的包
- 二、梯度检验的工作原理
- 三、一维梯度检验
- 四、多维梯度检验
- 五、总结
- 六、源代码
〇、作业目标和作业背景
欢迎来到本周最后一个任务!在这个任务中你将学习完善和使用梯度检验。
你是移动支付团队的一位成员,你需要将移动支付完善得更为全面,并且需要建立一个深度学习模型来在任何人进行支付时探测到是否诈骗。你想要知道在支付中是否有欺诈行为,例如用户的账户可能被黑客入侵。
本作业中反向传播的完善极具挑战性,并且有时候会存在一些bug。因为这是一个任务关键型应用程序(mission-critical application),你公司的CEO要确认你的反向传播函数是正确的。你的CEO说,“给我一个你的反向传播函数是完美运作的证明!”,为了给出这个保证,你需要使用“梯度检验”(gradient checking)。
让我们开始吧!
一、所需要使用的包
import numpy as np
from testCases import *
from gc_utils import sigmoid, relu, dictionary_to_vector, vector_to_dictionary, gradients_to_vector
numpy包可以使用Anaconda进行安装。安装的方式见此篇文章:【深度学习】吴恩达深度学习-Course1神经网络与深度学习-第二周神经网络基础编程中的使用环境部分,安装sklearn包时请使用命令:conda install scikit-learn而不是conda install sklearn。
testCases、gc_utils请参考上面的资料下载。
二、梯度检验的工作原理
反向传播计算梯度
,θ 代表模型参数。J是利用前向传播和你的损失函数计算出来的。
因为前向传播的完善相对来说比较简单,你非常有自信能够将它写对,因此你已经100%确信你计算的成本J是正确的。因此,你可以使用你计算J的代码来验证计算 ∂ J ∂ θ \frac{\partial J}{\partial θ} ∂θ∂J的代码。
让我们回顾一下导数(或梯度)的定义:
∂ J ∂ θ = lim ε → 0 J ( θ + ε ) − J ( θ − ε ) 2 ε \frac{\partial J}{\partial θ}=\lim\limits_{ε \to 0}\frac{J(θ+ε) - J(θ-ε)}{2ε} ∂θ∂J=ε→0lim2εJ(θ+ε)−J(θ−ε)
如果你对 lim ε → 0 \lim\limits_{ε \to 0} ε→0lim并不熟悉,没关系,这意思是:“当ε非常非常小”。
我们现在知道以下两件事:
- ∂ J ∂ θ \frac{\partial J}{\partial θ} ∂θ∂J是你想要确保计算正确的东西。
- 你可以计算 J ( θ + ε ) J(θ+ε) J(θ+ε)和 J ( θ − ε ) J(θ-ε) J(θ−ε)(在案例中,θ是一个实数),因为你确信J的实现是正确的。
让我们使用上边回顾的导数的定义和一个值非常小的ε来说服你的CEO你的代码计算出来的 ∂ J ∂ θ \frac{\partial J}{\partial θ} ∂θ∂J是正确的!
三、一维梯度检验
考虑一维的线性函数 J ( θ ) = θ x J(θ) = θx J(θ)=θx。该模型只包含一个实值参数θ,并以 x x x作为输入。
你将完成计算 J ( . ) J(.) J(.)的代码和其微分 ∂ J ∂ θ \frac{\partial J}{\partial θ} ∂θ∂J,你将用梯度检验来确保你对J的微分计算是正确的。

图1:一维线性模型
上边的这张图展示了计算的关键步骤:首先以 x x x为起点,然后计算函数 J ( x ) J(x) J(x)(前向传播)。然后计算微分 ∂ J ∂ θ \frac{\partial J}{\partial θ} ∂θ∂J(反向传播)。
练习1: 完善“前向传播”和“反向传播”。即计算 J ( . ) J(.) J(.)(前向传播)和它对θ的微分(反向传播)。接下来将完成前向传播部分。
def forward_propagation(x, theta):
"""
Implement the linear forward propagation (compute J) presented in Figure 1 (J(theta) = theta * x)
Arguments:
x -- a real-valued input
theta -- our parameter, a real number as well
Returns:
J -- the value of function J, computed using the formula J(theta) = theta * x
"""
完成后应当如下:
所给出的备注中已经提示了返回值:J - 函数J的值,用公式J(theta)= theta * x计算
def forward_propagation(x, theta):
"""
Implement the linear forward propagation (compute J) presented in Figure 1 (J(theta) = theta * x)
Arguments:
x -- a real-valued input
theta -- our parameter, a real number as well
Returns:
J -- the value of function J, computed using the formula J(theta) = theta * x
"""
J = np.dot(theta, x)
return J
欲要检验你这个函数写的是否正确,请使用以下代码:
# 测试forward_propagation(x, theta)
x, theta = 2, 4
J = forward_propagation(x, theta)
print ("J = " + str(J))
结果为:
J = 8
练习2: 现在,完善图一中提及的反向传播的步骤(微分计算)。即计算 J ( θ ) = θ x J(θ) = θx J(θ)=θx对于θ的微分。为了避免做微积分,你应当知道: d t h e t a = ∂ J ∂ θ = x dtheta = \frac{\partial J}{\partial θ} = x dtheta=∂θ∂J=x
# GRADED FUNCTION: backward_propagation
def backward_propagation(x, theta):
"""
Computes the derivative of J with respect to theta (see Figure 1).
Arguments:
x -- a real-valued input
theta -- our parameter, a real number as well
Returns:
dtheta -- the gradient of the cost with respect to theta
"""
完成后应当如下:
很简单,通过练习题目给出的提示,为了避免计算微积分,我们可以一眼就看出 J ( θ ) = θ x J(θ) = θx J(θ)=θx对于θ的微分为x,直接令其等同于dtheta就可以了。
可以用以下代码进行以下测试,看看结果是否正确
# 测试backward_propagation(x, theta)
x, theta = 2, 4
dtheta = backward_propagation(x, theta)
print ("dtheta = " + str(dtheta))
结果如下:
dtheta = 2
练习3: 为了证明backward_propagation()函数在计算梯度 ∂ J ∂ θ \frac{\partial J}{\partial θ} ∂θ∂J是完全正确的,让我们完善梯度检验函数吧。
说明:
- 首先使用上边的梯度定义和一个极小ε的计算“gradapprox”。这里有接下来的步骤:
- θ + = θ + ε θ^+ = θ + ε θ+=θ+ε
- θ − = θ − ε θ^- = θ - ε θ−=θ−ε
- J + = J ( θ + ) J^+ = J(θ^+) J+=J(θ+)
- J − = J ( θ − ) J^- = J(θ^-) J−=J(θ−)
- g r a d a p p r o x = J + − J − 2 ε gradapprox=\frac{J^+- J^-}{2ε} gradapprox=2εJ+−J−
- 然后,使用反向传播计算梯度,并且将结果存储在变量“grad”中
- 最后,使用下面的公式计算“gradapprox”和“grad”的相对差异:
d i f f e r e n c e = ∣ ∣ g r a d − g r a d a p p r o x ∣ ∣ 2 ∣ ∣ g r a d ∣ ∣ 2 + ∣ ∣ g r a d a p p r o x ∣ ∣ 2 difference = \frac{||grad - gradapprox||_2}{||grad||_2 + ||gradapprox||_2} difference=∣∣grad∣∣2+∣∣gradapprox∣∣2∣∣grad−gradapprox∣∣2
你需要使用三步来计算这个公式:
- 使用
np.linalg.norm(...)来计算分子 - 你需要两次调用
np.linalg.norm(...)来计算分母 - 将它们相除
- 如果difference的值非常小(小于 1 0 − 7 10^{-7} 10−7),你可以肯定你计算的梯度是完全正确的。否则,在你的梯度计算中,可能存在某些问题。
阅读完以上,请完成以下梯度检验函数:
def gradient_check(x, theta, epsilon=1e-7):
"""
Implement the backward propagation presented in Figure 1.
Arguments:
x -- a real-valued input
theta -- our parameter, a real number as well
epsilon -- tiny shift to the input to compute approximated gradient with formula(1)
Returns:
difference -- difference (2) between the approximated gradient and the backward propagation gradient
"""
完成后结果应当如下:
def gradient_check(x, theta, epsilon=1e-7):
"""
Implement the backward propagation presented in Figure 1.
Arguments:
x -- a real-valued input
theta -- our parameter, a real number as well
epsilon -- tiny shift to the input to compute approximated gradient with formula(1)
Returns:
difference -- difference (2) between the approximated gradient and the backward propagation gradient
"""
thetaplus = theta + epsilon
thetaminus = theta - epsilon
J_plus = forward_propagation(x, thetaplus)
J_minus = forward_propagation(x, thetaminus)
gradapprox = (J_plus - J_minus) / (2 * epsilon)
grad = backward_propagation(x, theta)
numerator = np.linalg.norm(grad - gradapprox)
denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox)
difference = numerator / denominator
if difference < 1e-7:
print("梯度是正确的!")
else:
print("梯度是错误的!")
return difference
用以下代码测试你写的是否正确:
# 测试gradient_check(x, theta, epsilon=1e-7)
x, theta = 2, 4
difference = gradient_check(x, theta)
print("difference = " + str(difference))
得到的答案应为:
梯度是正确的!
difference = 2.919335883291695e-10
恭喜,difference比 1 0 − 7 10^{-7} 10−7这个界限要小,所以你可以非常自信地说你的反向传播函数backward_propagation()的实现是正确的。
现在,在更多的真实案例中,你的成本函数 J J J有多余一维的输入。当你在训练神经网络时, θ θ θ成为了多个矩阵 W [ l ] W^{[l]} W[l]和 b [ l ] b^{[l]} b[l]的一部分!知道如何在多维输入的情况下完成梯度检验同样是很重要的,让我们来试一试!
四、多维梯度检验
接下来的图描述了你欺诈预测模型的前向和反向传播。

图2:深度神经网络
LINEAR->RELU->LINEAR->RELU->LINEAR->SIGMOID
让我们看看你完成的前向传播函数和反向传播函数,如下:
def forward_propagation_n(X, Y, parameters):
"""
Implements the forward propagation (and computes the cost) presented in Figure 3.
Arguments:
X -- training set for m examples
Y -- labels for m examples
parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
W1 -- weight matrix of shape (5, 4)
b1 -- bias vector of shape (5, 1)
W2 -- weight matrix of shape (3, 5)
b2 -- bias vector of shape (3, 1)
W3 -- weight matrix of shape (1, 3)
b3 -- bias vector of shape (1, 1)
Returns:
cost -- the cost function (logistic cost for one example)
"""
# retrieve parameters
m = X.shape[1]
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
W3 = parameters["W3"]
b3 = parameters["b3"]
# LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)
Z2 = np.dot(W2, A1) + b2
A2 = relu(Z2)
Z3 = np.dot(W3, A2) + b3
A3 = sigmoid(Z3)
# Cost
logprobs = np.multiply(-np.log(A3), Y) + np.multiply(-np.log(1 - A3), 1 - Y)
cost = 1. / m * np.sum(logprobs)
cache = (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3)
return cost, cache
现在,看一看反向传播函数
def backward_propagation_n(X, Y, cache):
"""
Implement the backward propagation presented in figure 2.
Arguments:
X -- input datapoint, of shape (input size, 1)
Y -- true "label"
cache -- cache output from forward_propagation_n()
Returns:
gradients -- A dictionary with the gradients of the cost with respect to each parameter, activation and pre-activation variables.
"""
m = X.shape[1]
(Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = 1. / m * np.dot(dZ3, A2.T)
db3 = 1. / m * np.sum(dZ3, axis=1, keepdims=True)
dA2 = np.dot(W3.T, dZ3)
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1. / m * np.dot(dZ2, A1.T) * 2 # Should not multiply by 2
db2 = 1. / m * np.sum(dZ2, axis=1, keepdims=True)
dA1 = np.dot(W2.T, dZ2)
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1. / m * np.dot(dZ1, X.T)
db1 = 4. / m * np.sum(dZ1, axis=1, keepdims=True) # Should not multiply by 4
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,
"dA2": dA2, "dZ2": dZ2, "dW2": dW2, "db2": db2,
"dA1": dA1, "dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
你从欺诈探测模型的测试中获得了一些结果,但是你不能够百分百相信你的模型。没有任何人是完美的!让我们完成梯度检验以证明你的梯度是正确的。
如何做梯度检验?
正如上面两大点(梯度检验的工作原理、一维梯度检验)所说,你想要比较“gradapprox”和反向传播计算出来的梯度,公式仍然如下:
∂ J ∂ θ = lim ε → 0 J ( θ + ε ) − J ( θ − ε ) 2 ε \frac{\partial J}{\partial θ}=\lim\limits_{ε \to 0}\frac{J(θ+ε) - J(θ-ε)}{2ε} ∂θ∂J=ε→0lim2εJ(θ+ε)−J(θ−ε)
然而,θ不再是一个标量。更标准地来说我们应该称之为“参数”。我们为你完成了dictionary_to_vector()函数。它能够将“parameters”字典转换成为一个叫做“values”的向量,包括将所有的参数(W1, b1, W2, b2, W3, b3)重塑为向量并连接它们。
相反的函数叫做vector_to_dictionary,输出为“parameters”字典。
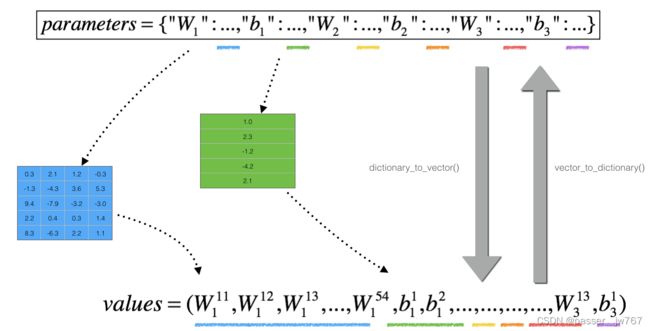
图3: dictionary_to_vector()和vector_to_dictionary()
你将会在gradient_check_n()中用到这些参数。
我们同样需要使用gradients_to_vector().将“gradients”字典转换称为向量“grad”。你不需要担心这一点。
练习: 这里有能够帮助你完成梯度检验的伪代码:
For each i in num_parameters:
- 计算 J_plus[i]:
- 设置 θ + θ^+ θ+为
np.copy(parameters_values) - 设置 θ i + θ^+_i θi+为 θ i + + ε θ^+_i +ε θi++ε
- 使用
forward_propagation_n(x, y, vector_to_dictionary(θ + θ^+ θ+))计算 J i + J^+_i Ji+
- 计算
J_minus[i]:对 θ − θ^- θ−做同样的事 - 计算 g r a d a p p r o x [ i ] = J i + − J i − 2 ε gradapprox[i]=\frac{J^+_i - J^-_i}{2ε} gradapprox[i]=2εJi+−Ji−
因此,你获得了一个gradapprox向量,gradapprox[i]是梯度相对于参数值parameter_value[i]的近似值。你可以将这个gradapprox向量与反向传播得到的梯度向量进行比较。像一维案例中的(步骤1、2、3)计算一样:
d i f f e r e n c e = ∣ ∣ g r a d − g r a d a p p r o x ∣ ∣ 2 ∣ ∣ g r a d ∣ ∣ 2 + ∣ ∣ g r a d a p p r o x ∣ ∣ 2 difference = \frac{||grad - gradapprox||_2}{||grad||_2 + ||gradapprox||_2} difference=∣∣grad∣∣2+∣∣gradapprox∣∣2∣∣grad−gradapprox∣∣2
完成以下函数:
def gradient_check_n(parameters, gradients, X, Y, epsilon=1e-7):
"""
Checks if backward_propagation_n computes correctly the gradient of the cost output by forward_propagation_n
Arguments:
parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
grad -- output of backward_propagation_n, contains gradients of the cost with respect to the parameters.
x -- input datapoint, of shape (input size, 1)
y -- true "label"
epsilon -- tiny shift to the input to compute approximated gradient with formula(1)
Returns:
difference -- difference (2) between the approximated gradient and the backward propagation gradient
"""
完成后如下:
def gradient_check_n(parameters, gradients, X, Y, epsilon=1e-7):
"""
Checks if backward_propagation_n computes correctly the gradient of the cost output by forward_propagation_n
Arguments:
parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
grad -- output of backward_propagation_n, contains gradients of the cost with respect to the parameters.
x -- input datapoint, of shape (input size, 1)
y -- true "label"
epsilon -- tiny shift to the input to compute approximated gradient with formula(1)
Returns:
difference -- difference (2) between the approximated gradient and the backward propagation gradient
"""
parameters_values = dictionary_to_vector(parameters)
grad = gradients_to_vector(gradients)
num_parameters = parameters_values[0]
J_plus = np.zeros((num_parameters, 1))
J_minus = np.zeros((num_parameters, 1))
gradapprox = np.zeros((num_parameters, 1))
for i in range(num_parameters):
thetaplus = np.copy(parameters_values)
thetaplus[i][0] += epsilon
J_plus[i] = forward_propagation(X, Y, vector_to_dictionary(thetaplus))
thetaminus = np.copy(parameters_values)
thetaminus[i][0] -= epsilon
J_minus[i] = forward_propagation(X, Y, vector_to_dictionary(thetaminus))
gradapprox[i] = (J_plus[i] - J_minus[i]) / (2 * epsilon)
numerator = np.linalg.norm(grad - gradapprox)
denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox)
difference = numerator / denominator
if difference > 1e-7:
print("\033[93m" + "There is a mistake in the backward propagation! difference = " + str(difference) + "\033[0m")
else:
print("\033[92m" + "Your backward propagation works perfectly fine! difference = " + str(difference) + "\033[0m")
return difference
用如下代码进行测试:
X, Y, parameters = gradient_check_n_test_case()
cost, cache = forward_propagation(X, parameters)
gradients = backward_propagation(X, Y, cache)
difference = gradient_check_n(parameters, gradients, X, Y)
得到的结果如下:
There is a mistake in the backward propagation! difference = 0.285093156781
这里代码可能会报错,因为缺失了部分,这里给出gradient_check)n_test_case()所在的testCase.py的完整代码。我将其重命名为testCaseNew.py,因为我已经有了一个testCase.py1了,如下:
import numpy as np
def compute_cost_with_regularization_test_case():
np.random.seed(1)
Y_assess = np.array([[1, 1, 0, 1, 0]])
W1 = np.random.randn(2, 3)
b1 = np.random.randn(2, 1)
W2 = np.random.randn(3, 2)
b2 = np.random.randn(3, 1)
W3 = np.random.randn(1, 3)
b3 = np.random.randn(1, 1)
parameters = {"W1": W1, "b1": b1, "W2": W2, "b2": b2, "W3": W3, "b3": b3}
a3 = np.array([[ 0.40682402, 0.01629284, 0.16722898, 0.10118111, 0.40682402]])
return a3, Y_assess, parameters
def backward_propagation_with_regularization_test_case():
np.random.seed(1)
X_assess = np.random.randn(3, 5)
Y_assess = np.array([[1, 1, 0, 1, 0]])
cache = (np.array([[-1.52855314, 3.32524635, 2.13994541, 2.60700654, -0.75942115],
[-1.98043538, 4.1600994 , 0.79051021, 1.46493512, -0.45506242]]),
np.array([[ 0. , 3.32524635, 2.13994541, 2.60700654, 0. ],
[ 0. , 4.1600994 , 0.79051021, 1.46493512, 0. ]]),
np.array([[-1.09989127, -0.17242821, -0.87785842],
[ 0.04221375, 0.58281521, -1.10061918]]),
np.array([[ 1.14472371],
[ 0.90159072]]),
np.array([[ 0.53035547, 5.94892323, 2.31780174, 3.16005701, 0.53035547],
[-0.69166075, -3.47645987, -2.25194702, -2.65416996, -0.69166075],
[-0.39675353, -4.62285846, -2.61101729, -3.22874921, -0.39675353]]),
np.array([[ 0.53035547, 5.94892323, 2.31780174, 3.16005701, 0.53035547],
[ 0. , 0. , 0. , 0. , 0. ],
[ 0. , 0. , 0. , 0. , 0. ]]),
np.array([[ 0.50249434, 0.90085595],
[-0.68372786, -0.12289023],
[-0.93576943, -0.26788808]]),
np.array([[ 0.53035547],
[-0.69166075],
[-0.39675353]]),
np.array([[-0.3771104 , -4.10060224, -1.60539468, -2.18416951, -0.3771104 ]]),
np.array([[ 0.40682402, 0.01629284, 0.16722898, 0.10118111, 0.40682402]]),
np.array([[-0.6871727 , -0.84520564, -0.67124613]]),
np.array([[-0.0126646]]))
return X_assess, Y_assess, cache
def forward_propagation_with_dropout_test_case():
np.random.seed(1)
X_assess = np.random.randn(3, 5)
W1 = np.random.randn(2, 3)
b1 = np.random.randn(2, 1)
W2 = np.random.randn(3, 2)
b2 = np.random.randn(3, 1)
W3 = np.random.randn(1, 3)
b3 = np.random.randn(1, 1)
parameters = {"W1": W1, "b1": b1, "W2": W2, "b2": b2, "W3": W3, "b3": b3}
return X_assess, parameters
def backward_propagation_with_dropout_test_case():
np.random.seed(1)
X_assess = np.random.randn(3, 5)
Y_assess = np.array([[1, 1, 0, 1, 0]])
cache = (np.array([[-1.52855314, 3.32524635, 2.13994541, 2.60700654, -0.75942115],
[-1.98043538, 4.1600994 , 0.79051021, 1.46493512, -0.45506242]]), np.array([[ True, False, True, True, True],
[ True, True, True, True, False]], dtype=bool), np.array([[ 0. , 0. , 4.27989081, 5.21401307, 0. ],
[ 0. , 8.32019881, 1.58102041, 2.92987024, 0. ]]), np.array([[-1.09989127, -0.17242821, -0.87785842],
[ 0.04221375, 0.58281521, -1.10061918]]), np.array([[ 1.14472371],
[ 0.90159072]]), np.array([[ 0.53035547, 8.02565606, 4.10524802, 5.78975856, 0.53035547],
[-0.69166075, -1.71413186, -3.81223329, -4.61667916, -0.69166075],
[-0.39675353, -2.62563561, -4.82528105, -6.0607449 , -0.39675353]]), np.array([[ True, False, True, False, True],
[False, True, False, True, True],
[False, False, True, False, False]], dtype=bool), np.array([[ 1.06071093, 0. , 8.21049603, 0. , 1.06071093],
[ 0. , 0. , 0. , 0. , 0. ],
[ 0. , 0. , 0. , 0. , 0. ]]), np.array([[ 0.50249434, 0.90085595],
[-0.68372786, -0.12289023],
[-0.93576943, -0.26788808]]), np.array([[ 0.53035547],
[-0.69166075],
[-0.39675353]]), np.array([[-0.7415562 , -0.0126646 , -5.65469333, -0.0126646 , -0.7415562 ]]), np.array([[ 0.32266394, 0.49683389, 0.00348883, 0.49683389, 0.32266394]]), np.array([[-0.6871727 , -0.84520564, -0.67124613]]), np.array([[-0.0126646]]))
return X_assess, Y_assess, cache
def gradient_check_n_test_case():
np.random.seed(1)
x = np.random.randn(4,3)
y = np.array([1, 1, 0])
W1 = np.random.randn(5,4)
b1 = np.random.randn(5,1)
W2 = np.random.randn(3,5)
b2 = np.random.randn(3,1)
W3 = np.random.randn(1,3)
b3 = np.random.randn(1,1)
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2,
"W3": W3,
"b3": b3}
return x, y, parameters
但是forward_propagation_n(X, Y, parameters)和backward_propagation_n(X, Y, cache)实在不知道是啥。。所以我只是贴了标准的运行结果,并不知道这里跑起来会是怎么样的。。接下来一小部分是翻译了原作者(参考链接1)的话
似乎在我们给你的backward_propagation_n代码中存在一些问题!(因为使用gradient_check_n()得到的difference的值比较大)你很好地完成了梯度检验。回头看看backward_propagation并尝试找到和纠正那些错误(提示:检查dW2和db1)。在你修改好它以后,重新跑一下梯度检验。记住,如果你修改了代码,你将需要重新调用定义backward_propagation_n()
你能够理解通过梯度检验发现潜在的计算问题吗?即使这一部分的任务并没有评分,我们强烈的希望你能够尝试找到bug并重新运行梯度检验直到你确信backprop反向传播已经完全地修改好了。
五、总结
笔记:
- 梯度检验很慢!近似梯度 ∂ J ∂ θ ≈ lim ε → 0 J ( θ + ε ) − J ( θ − ε ) 2 ε \frac{\partial J}{\partial θ}≈\lim\limits_{ε \to 0}\frac{J(θ+ε) - J(θ-ε)}{2ε} ∂θ∂J≈ε→0lim2εJ(θ+ε)−J(θ−ε)的计算是很耗时的。因为这个原因,我们不能够在每一次迭代中都使用梯度检验。只是使用几次来保证梯度是正确的
- 至少我们已经介绍过梯度检验不能和dropout同时实施。在不使用dropout的情况下你可以经常跑梯度检验算法来确保你的backprop反向传播是正确的,然后再使用dropout。
恭喜,你可以自信的说你欺诈预测的深度学习模型是完全正确的!你甚至可以用这个来说服你的CEO.
你在本篇文章中能够知道什么?
- 梯度检查验证反向传播梯度和梯度数值之间的接近程度(使用前向传播计算)。
- 梯度检验很慢,所以我们我们不能再训练的每一次迭代中都使用梯度检验。你将时常使用梯度检验来确保你的代码是正确的,然后关闭梯度检验,在学习过程中使用真正的backprop反向传播。
六、源代码
import numpy as np
from course2.week1.testCases import *
from course2.week1.gc_utils import sigmoid, relu, dictionary_to_vector, vector_to_dictionary, gradients_to_vector
# testCasesNew请见文末testCase.py源代码
from course2.week1.testCasesNew import *
from course2.week1.reg_utils import *
def forward_propagation(x, theta):
"""
Implement the linear forward propagation (compute J) presented in Figure 1 (J(theta) = theta * x)
Arguments:
x -- a real-valued input
theta -- our parameter, a real number as well
Returns:
J -- the value of function J, computed using the formula J(theta) = theta * x
"""
J = np.dot(theta, x)
return J
# # 测试forward_propagation(x, theta)
# x, theta = 2, 4
# J = forward_propagation(x, theta)
# print ("J = " + str(J))
def backward_propagation(x, theta):
"""
Computes the derivative of J with respect to theta (see Figure 1).
Arguments:
x -- a real-valued input
theta -- our parameter, a real number as well
Returns:
dtheta -- the gradient of the cost with respect to theta
"""
### START CODE HERE ### (approx. 1 line)
dtheta = x
### END CODE HERE ###
return dtheta
# # 测试backward_propagation(x, theta)
# x, theta = 2, 4
# dtheta = backward_propagation(x, theta)
# print ("dtheta = " + str(dtheta))
def gradient_check(x, theta, epsilon=1e-7):
"""
Implement the backward propagation presented in Figure 1.
Arguments:
x -- a real-valued input
theta -- our parameter, a real number as well
epsilon -- tiny shift to the input to compute approximated gradient with formula(1)
Returns:
difference -- difference (2) between the approximated gradient and the backward propagation gradient
"""
thetaplus = theta + epsilon
thetaminus = theta - epsilon
J_plus = forward_propagation(x, thetaplus)
J_minus = forward_propagation(x, thetaminus)
gradapprox = (J_plus - J_minus) / (2 * epsilon)
grad = backward_propagation(x, theta)
numerator = np.linalg.norm(grad - gradapprox)
denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox)
difference = numerator / denominator
if difference < 1e-7:
print("梯度是正确的!")
else:
print("梯度是错误的!")
return difference
# # 测试gradient_check(x, theta, epsilon=1e-7)
# x, theta = 2, 4
# difference = gradient_check(x, theta)
# print("difference = " + str(difference))
def gradient_check_n(parameters, gradients, X, Y, epsilon=1e-7):
"""
Checks if backward_propagation_n computes correctly the gradient of the cost output by forward_propagation_n
Arguments:
parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
grad -- output of backward_propagation_n, contains gradients of the cost with respect to the parameters.
x -- input datapoint, of shape (input size, 1)
y -- true "label"
epsilon -- tiny shift to the input to compute approximated gradient with formula(1)
Returns:
difference -- difference (2) between the approximated gradient and the backward propagation gradient
"""
parameters_values = dictionary_to_vector(parameters)
grad = gradients_to_vector(gradients)
num_parameters = parameters_values[0]
J_plus = np.zeros((num_parameters, 1))
J_minus = np.zeros((num_parameters, 1))
gradapprox = np.zeros((num_parameters, 1))
for i in range(num_parameters):
thetaplus = np.copy(parameters_values)
thetaplus[i][0] += epsilon
J_plus[i] = forward_propagation(X, Y, vector_to_dictionary(thetaplus))
thetaminus = np.copy(parameters_values)
thetaminus[i][0] -= epsilon
J_minus[i] = forward_propagation(X, Y, vector_to_dictionary(thetaminus))
gradapprox[i] = (J_plus[i] - J_minus[i]) / (2 * epsilon)
numerator = np.linalg.norm(grad - gradapprox)
denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox)
difference = numerator / denominator
if difference > 1e-7:
print("\033[93m" + "There is a mistake in the backward propagation! difference = " + str(difference) + "\033[0m")
else:
print("\033[92m" + "Your backward propagation works perfectly fine! difference = " + str(difference) + "\033[0m")
return difference
X, Y, parameters = gradient_check_n_test_case()
# cost, cache = forward_propagation(X, parameters)
# gradients = backward_propagation(X, Y, cache)
# difference = gradient_check_n(parameters, gradients, X, Y)
testCase.py源代码 ↩︎