LeetCode 精选TOP面试题【51 ~ 100】
LeetCode 精选TOP面试题【51 ~ 100】
文章目录
- LeetCode 精选TOP面试题【51 ~ 100】
-
- [103. 二叉树的锯齿形层序遍历](https://leetcode-cn.com/problems/binary-tree-zigzag-level-order-traversal/)
-
- (反转层序遍历)
- (双栈)
- [剑指 Offer 11. 旋转数组的最小数字](https://leetcode-cn.com/problems/xuan-zhuan-shu-zu-de-zui-xiao-shu-zi-lcof/)
-
- (二分)
- [611. 有效三角形的个数](https://leetcode-cn.com/problems/valid-triangle-number/)
-
- (双指针)
- [剑指 Offer 29. 顺时针打印矩阵](https://leetcode-cn.com/problems/shun-shi-zhen-da-yin-ju-zhen-lcof/)
-
- (偏移量)
- [199. 二叉树的右视图](https://leetcode-cn.com/problems/binary-tree-right-side-view/)
-
- (广搜)
- (深搜)
- [148. 排序链表](https://leetcode-cn.com/problems/sort-list/)
-
- (排序链表)
- (归并排序链表)
- (迭代版归并排序)
- [543. 二叉树的直径](https://leetcode-cn.com/problems/diameter-of-binary-tree/)
-
- (递归)
- [31. 下一个排列](https://leetcode-cn.com/problems/next-permutation/)
-
- (脑力+全排列)
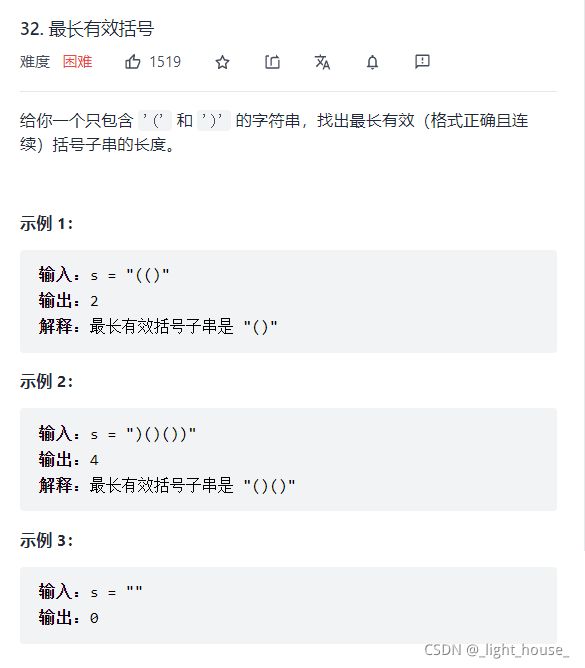
- [32. 最长有效括号](https://leetcode-cn.com/problems/longest-valid-parentheses/)
-
- (栈)
- (正向逆向法)
- (动规)
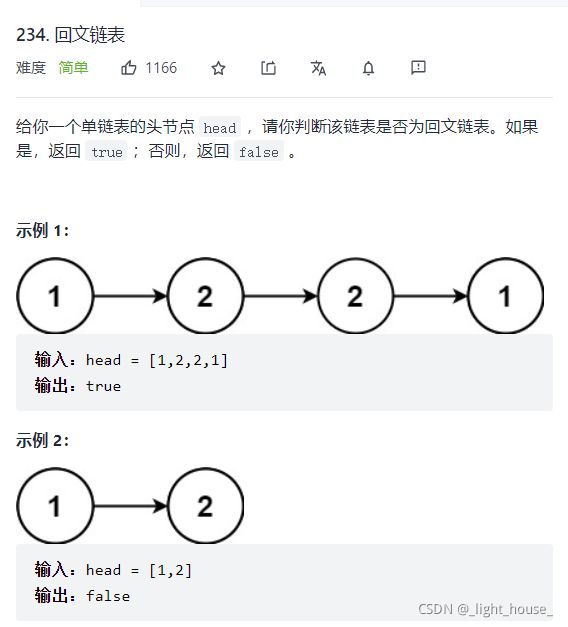
- [234. 回文链表](https://leetcode-cn.com/problems/palindrome-linked-list/)
-
- (反转链表)
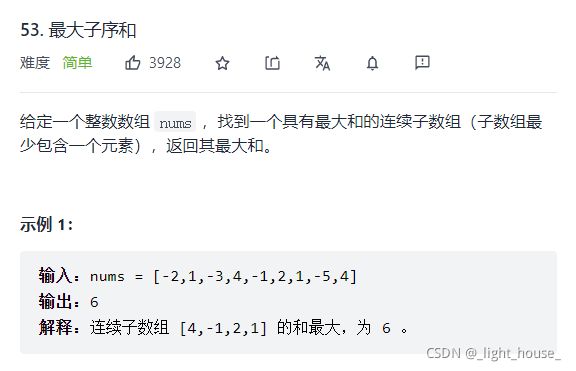
- [53. 最大子序和](https://leetcode-cn.com/problems/maximum-subarray/)
-
- (动规)
- (贪心)
- [322. 零钱兑换](https://leetcode-cn.com/problems/coin-change/)
-
- (动规)
- (动规-一维空间优化)
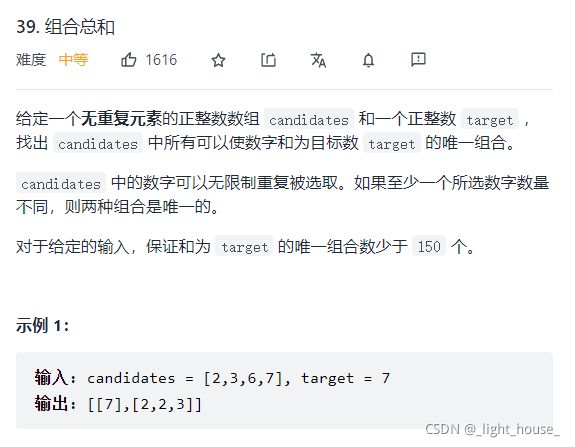
- [39. 组合总和](https://leetcode-cn.com/problems/combination-sum/)
-
- (排序优化+爆搜)
- [35. 搜索插入位置](https://leetcode-cn.com/problems/search-insert-position/)
-
- (二分)
- [283. 移动零](https://leetcode-cn.com/problems/move-zeroes/)
-
- (下标索引双指针)
- [165. 比较版本号](https://leetcode-cn.com/problems/compare-version-numbers/)
-
- (双指针)
- [剑指 Offer 04. 二维数组中的查找](https://leetcode-cn.com/problems/er-wei-shu-zu-zhong-de-cha-zhao-lcof/)
-
- (找规律)
- [面试题 17.24. 最大子矩阵](https://leetcode-cn.com/problems/max-submatrix-lcci/)
-
- (二维最大子序和)
- [139. 单词拆分](https://leetcode-cn.com/problems/word-break/)
-
- (动规)
- (字符串哈希+动规)
- (字符串哈希(反向)+动规)
- [198. 打家劫舍](https://leetcode-cn.com/problems/house-robber/)
-
- (动规)
- [136. 只出现一次的数字](https://leetcode-cn.com/problems/single-number/)
-
- (异或运算)
- [69. Sqrt(x)](https://leetcode-cn.com/problems/sqrtx/)
-
- (二分)
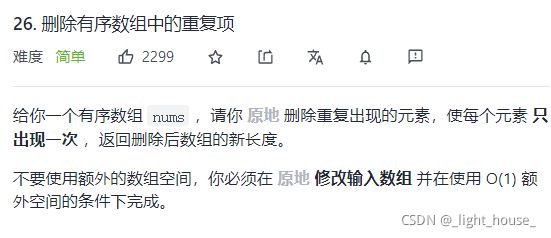
- [26. 删除有序数组中的重复项](https://leetcode-cn.com/problems/remove-duplicates-from-sorted-array/)
-
- (双指针)
- (双指针2)
- (库函数)
- [84. 柱状图中最大的矩形](https://leetcode-cn.com/problems/largest-rectangle-in-histogram/)
-
- (单调栈)
- (保存单调栈)
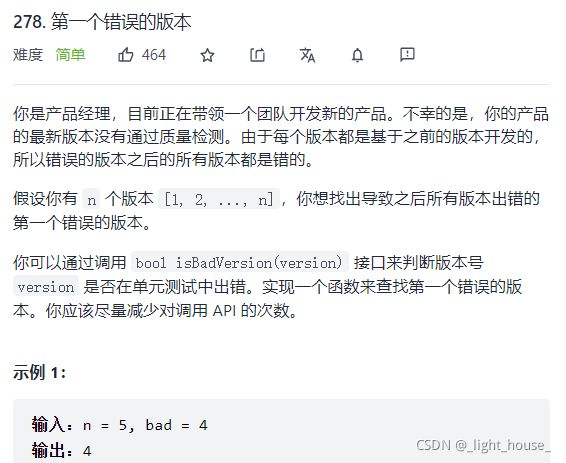
- [278. 第一个错误的版本](https://leetcode-cn.com/problems/first-bad-version/)
-
- (二分)
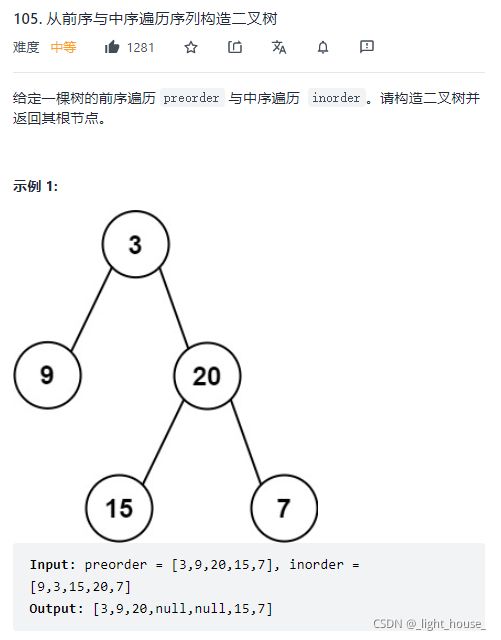
- [105. 从前序与中序遍历序列构造二叉树](https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/)
-
- (哈希表+递归)
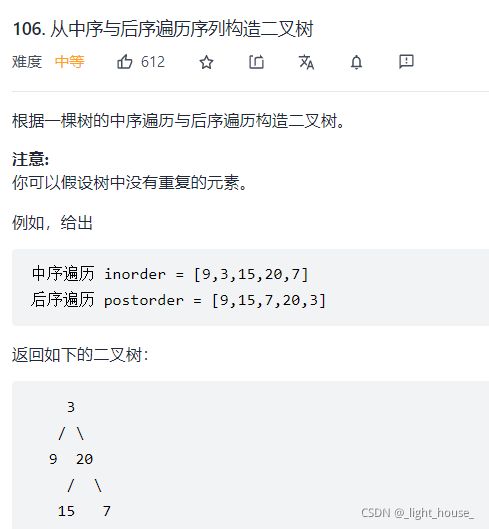
- [106. 从中序与后序遍历序列构造二叉树](https://leetcode-cn.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/)
-
- (哈希表定位+递归)
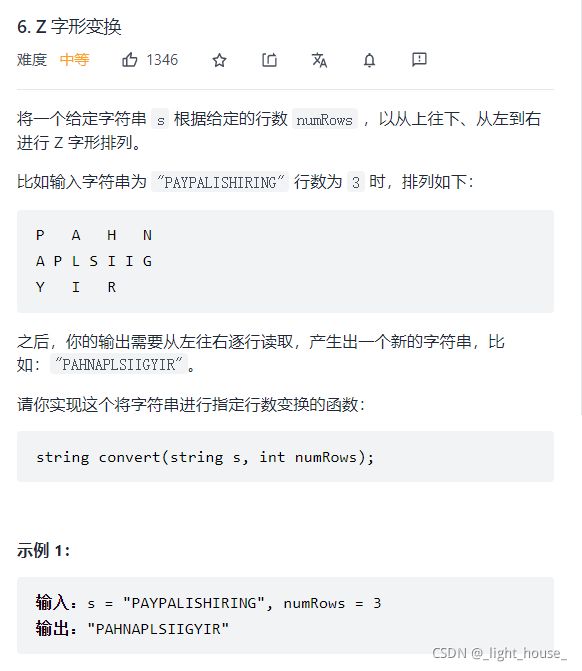
- [6. Z 字形变换](https://leetcode-cn.com/problems/zigzag-conversion/)
-
- (找规律)
- (找规律2)
- (找规律-蛇形矩阵)
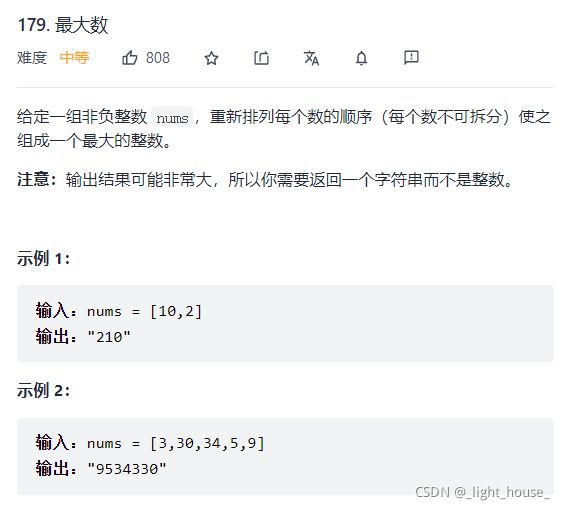
- [179. 最大数](https://leetcode-cn.com/problems/largest-number/)
-
- (贪心+排序)
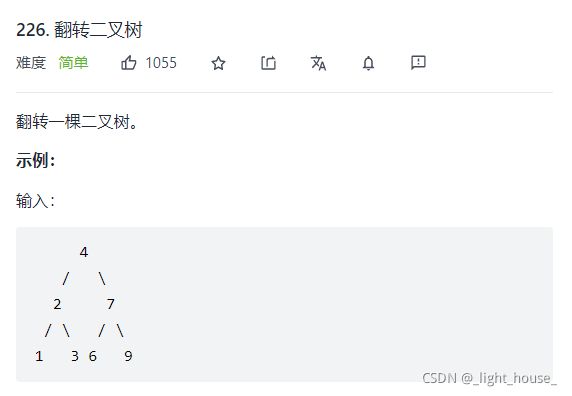
- [226. 翻转二叉树](https://leetcode-cn.com/problems/invert-binary-tree/)
-
- (递归)
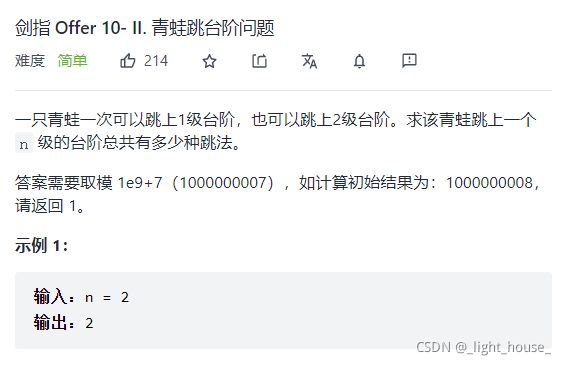
- [剑指 Offer 10- II. 青蛙跳台阶问题](https://leetcode-cn.com/problems/qing-wa-tiao-tai-jie-wen-ti-lcof/)
-
- (动规)
- (完全背包解法)
- 进阶问题(变态青蛙跳台阶)
- (找规律)
- [剑指 Offer 13. 机器人的运动范围](https://leetcode-cn.com/problems/ji-qi-ren-de-yun-dong-fan-wei-lcof/)
-
- (dfs)
- (bfs)
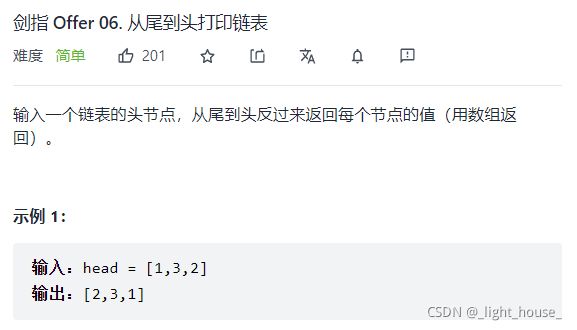
- [剑指 Offer 06. 从尾到头打印链表](https://leetcode-cn.com/problems/cong-wei-dao-tou-da-yin-lian-biao-lcof/)
-
- (栈)
- (反转链表)
- (递归)
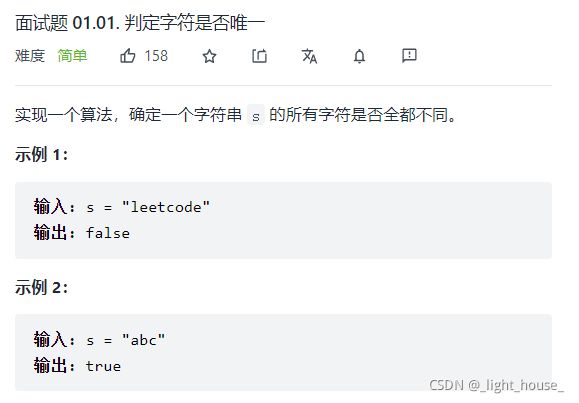
- [面试题 01.01. 判定字符是否唯一](https://leetcode-cn.com/problems/is-unique-lcci/)
-
- (位运算)
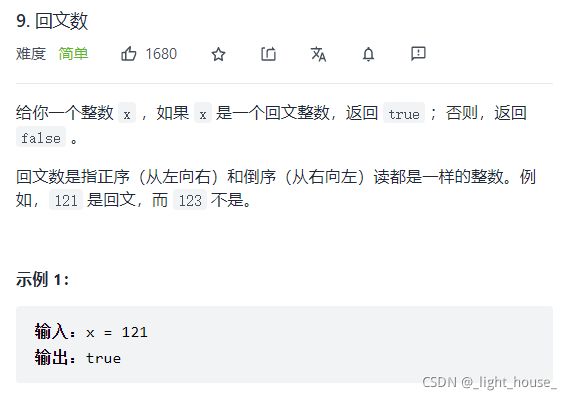
- [9. 回文数](https://leetcode-cn.com/problems/palindrome-number/)
-
- (字符串+双指针)
- (快速写法)
- (整数反转)
- (反转半边)
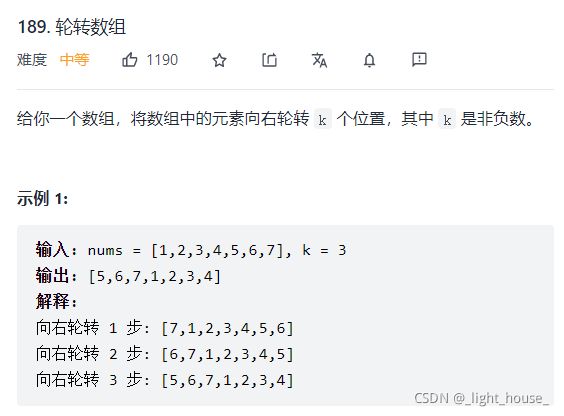
- [189. 轮转数组](https://leetcode-cn.com/problems/rotate-array/)
-
- (两次反转)
- [17. 电话号码的字母组合](https://leetcode-cn.com/problems/letter-combinations-of-a-phone-number/)
-
- (dfs-回溯)
- [剑指 Offer 40. 最小的k个数](https://leetcode-cn.com/problems/zui-xiao-de-kge-shu-lcof/)
-
- (小根堆)
- 3.无重复字符的最长子串
-
- (双指针 + 滑动窗口)
- (滑动窗口简洁版)
- 5.最长回文子串
-
- (动规)
- (中心扩展法)
- 7.整数反转
-
- (数字处理)
- [8. 字符串转换整数 (atoi)](https://leetcode-cn.com/problems/string-to-integer-atoi/)
-
- (字符串处理)
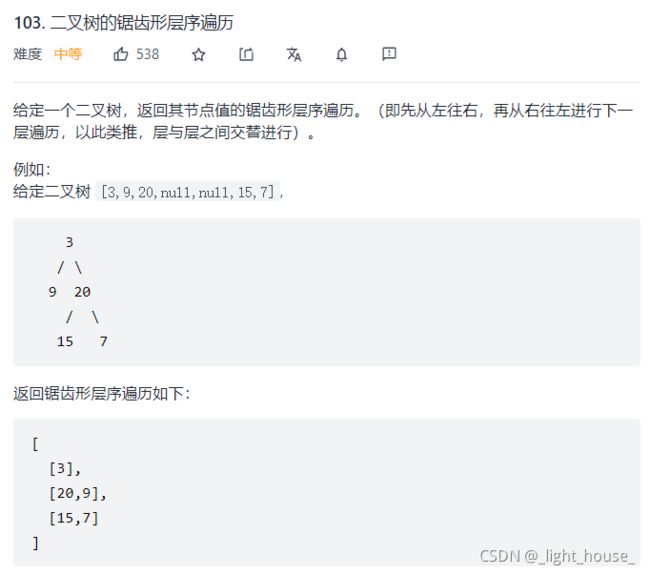
103. 二叉树的锯齿形层序遍历
(反转层序遍历)
本题其实就是层序遍历一个二叉树的升级版,我们需要要将二叉树层序遍历的结果放入答案中,然后将偶数层的节点结果逆置一遍即可。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
if (!root) return {};
vector<vector<int>> ans;
queue<TreeNode*> q;
q.push(root);
int step = 1;
while (!q.empty()) {
int size = q.size();
vector<int> path;
while (size --) {
auto top = q.front(); q.pop();
path.push_back(top->val);
if (top->left) q.push(top->left);
if (top->right) q.push(top->right);
}
if (step % 2 == 0) reverse(path.begin(), path.end());
ans.push_back(path);
step ++;
}
return ans;
}
};
(双栈)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
vector<vector<int>> ans;
if (!root) return ans;
stack<TreeNode*> odd;
stack<TreeNode*> even;
odd.push(root);
int flag = 1;
while (!odd.empty() || !even.empty()) {
vector<int> path;
if (flag > 0) {
while (!odd.empty()) {
auto top = odd.top(); odd.pop();
path.push_back(top->val);
if (top->left) even.push(top->left);
if (top->right) even.push(top->right);
}
} else {
while (!even.empty()) {
auto top = even.top(); even.pop();
path.push_back(top->val);
if (top->right) odd.push(top->right);
if (top->left) odd.push(top->left);
}
}
flag *= -1;
ans.push_back(path);
}
return ans;
}
};
剑指 Offer 11. 旋转数组的最小数字
(二分)
本题因为数组是有序数组拆分而成,所以数组局部还是具有单调性的。
如果一个数组没有被拆分成两个数组的话,那么直接返回这个有序数组的开头即可。
如果一个数组被拆分成了两个数组的话,那么被拆分后的数组的左右两边都是是一段有序的数组,并且左边一段数组都>nums.back(),右边一段数组都<=nums.back()。
根据这个特点就可以二分答案了,我们需要从左向右找出第一个
注意:因为有可能会有重复数字出现在数组中,所以被拆分的左边数组的前端和右边数组的后端可能会是重复的元素。但是这就不满足左数组中的数字都>nums.back()了,所以我们需要将右边数组后半段重复的数字去掉,这样就可以使得nums.back()都小于左边数组中的所有数组了。
class Solution {
public:
int minArray(vector<int>& nums) {
int n = nums.size();
if (nums[0] < nums.back()) return nums[0];
int l = 0, r = n - 1;
while (l < r && nums[0] == nums[r]) r --;
int target = nums[r];
while (l < r) {
int mid = l + (r - l) / 2;
if (nums[mid] <= target) r = mid;
else l = mid + 1;
}
return nums[l];
}
};
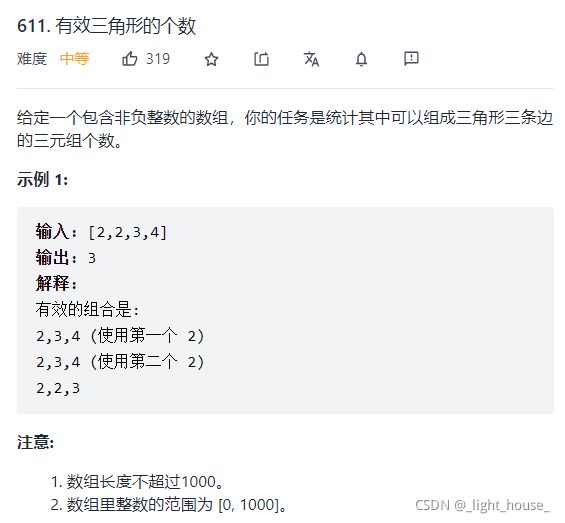
611. 有效三角形的个数
(双指针)
最暴力的方法应该是三重循环枚举三个数字。但是这样会超时。
经过观察可以发现,如果数组经过排序,那么从前往后判断三角形是否有效就可以利用最小的两条边相加是否大于最大的一条边来判断。
而且如果我们先枚举最大的一个数字nums[i]的话,那么nums[j] + nums[k]的和一定需要大于nums[i],而且因为数组是有序的,所以如果nums[j]减小的话,那么nums[k]就需要增大,这样才可以使得nums[j] + nums[k] > nums[i],因此可以利用这个单调性的原则使得我们可以使用双指针算法来解决本题。
class Solution {
public:
int triangleNumber(vector<int>& nums) {
int n = nums.size();
sort(nums.begin(), nums.end());
int ans = 0;
for (int i = 2; i < n; i ++) {
for (int j = i - 1, k = 0; k < j; j --) {
while (k < j && nums[k] + nums[j] <= nums[i]) k ++;
ans += j - k;
}
}
return ans;
}
};
总结:本题和「三数之和」很像,都是三个数加和为某一个值。然后我们可以通过排序过后,只用枚举其中一个数字和利用双指针就可以通过。
这么做的原因是因为已经有了排序和三个数的关系,所以只需要枚举一个数字,那么另两个数字的总和会是一个相对固定的值。利用总和不变和数组有序的原理,所以可以利用双指针解决这个问题。
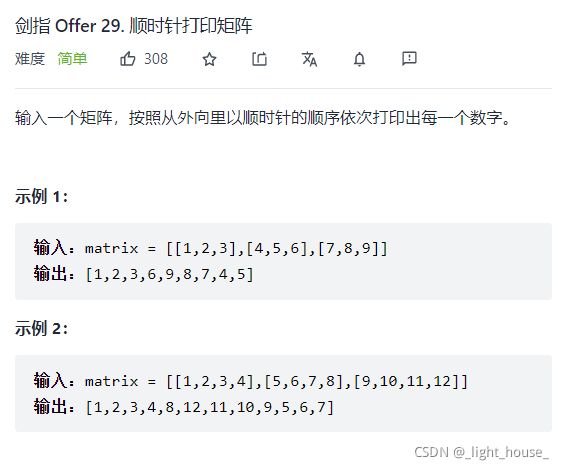
剑指 Offer 29. 顺时针打印矩阵
(偏移量)
其实本题就是一个偏移量的问题,我们需要数组转动起来,这可以使用偏移量数组来解决。利用int xd[4] = {0, 1, 0, -1}, yd[4] = {1, 0, -1, 0};使得数组可以顺时针旋转起来。除非越界或者已经被访问过了,否则按照原来的方向继续前进,否则的话,我们就需要手动的将转动的方向调整一下。
class Solution {
public:
const int INF = 0x3f3f3f3f;
vector<int> spiralOrder(vector<vector<int>>& matrix) {
if (matrix.empty()) return {};
int n = matrix.size(), m = matrix[0].size();
vector<int> ans;
int x = 0, y = 0, d = 0;
int xd[4] = {0, 1, 0, -1}, yd[4] = {1, 0, -1, 0};
vector<vector<bool>> vis(n, vector<bool>(m));
for (int i = 0; i < n * m; i ++) {
ans.push_back(matrix[x][y]);
vis[x][y] = true;
int a = x + xd[d], b = y + yd[d];
if (a < 0 || b < 0 || a >= n || b >= m || vis[a][b]) {
d = (d + 1) % 4;
a = x + xd[d], b = y + yd[d];
}
x = a, y = b;
}
return ans;
}
};
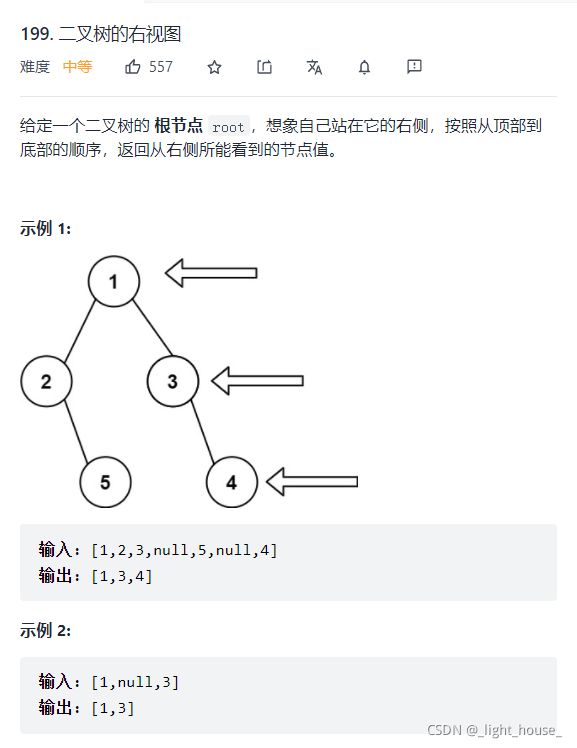
199. 二叉树的右视图
(广搜)
我们提取出每一层的最后一个节点,所以我们只需要使用层序遍历找到每一层的最后一个节点,然后放入ans中即可。
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
vector<int> ans;
if (!root) return ans;
queue<TreeNode*> q;
q.push(root);
while (!q.empty()) {
int size = q.size();
while (size --) {
TreeNode* top = q.front();
q.pop();
if (!size) ans.push_back(top->val);
if (top->left) q.push(top->left);
if (top->right) q.push(top->right);
}
}
return ans;
}
};
(深搜)
class Solution {
public:
vector<int> ans;
void dfs(TreeNode* root, int depth) {
if (!root) return ;
if (depth == ans.size()) {
ans.push_back(root->val);
}
depth ++;
dfs(root->right, depth);
dfs(root->left, depth);
}
vector<int> rightSideView(TreeNode* root) {
if (!root) return ans;
dfs(root, 0);
return ans;
}
};
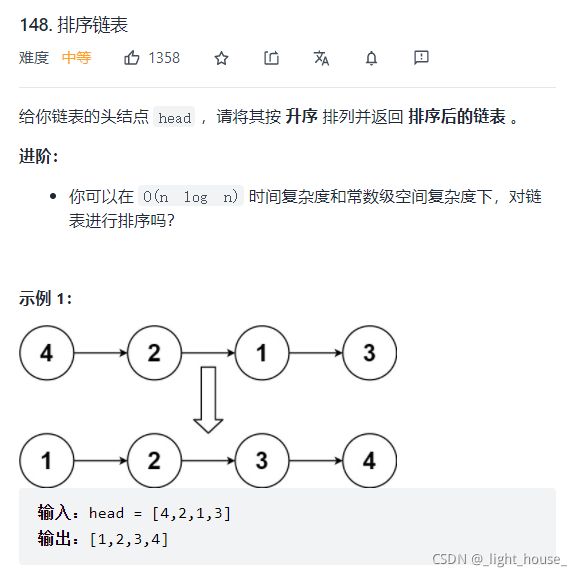
148. 排序链表
(排序链表)
class Solution {
public:
const int INF = 0x3f3f3f3f;
ListNode* Sort(ListNode* head) {
if (!head->next) return head;
ListNode* newHead = Sort(head->next);
ListNode* dummy = new ListNode(INF);
dummy->next = newHead;
ListNode* cur = newHead, *prev = dummy;
while (cur && cur->val < head->val) {
prev = cur;
cur = cur->next;
}
head->next = cur;
prev->next = head;
ListNode* ans = dummy->next;
delete dummy;
return ans;
}
ListNode* sortList(ListNode* head) {
if (!head) return nullptr;
return Sort(head);
}
};
(归并排序链表)
如果想要实现nlogn的时间复杂度的话,就必须使用二分的策略。所以我们可以使用归并排序来解决这个问题。
归并排序的核心思想就是合并两个一半的链表,所以我们先将链表从中间分割开来,然后将分割后的两个链表二路归并起来就可以了。
核心步骤:
1.利用快慢指针将链表从中间分成两半,并且两个链表需要成为独立的链表(尾指针都指向空)。
2.二路归并,每次都挑选出两个链表中较小节点作为链表的下一个节点。
注意:因为归并排序需要递归,所以空间复杂度为logn
class Solution {
public:
ListNode* sortList(ListNode* head) {
if (!head || !head->next) return head;
// 分割链表:找链表的中点
ListNode* slow = head, * fast = head;
ListNode* brk = nullptr;
while (fast && fast->next) {
fast = fast->next->next;
if (!fast || !fast->next) brk = slow;
slow = slow->next;
}
brk->next = nullptr;
ListNode* h1 = sortList(head);
ListNode* h2 = sortList(slow);
// 归并排序链表
ListNode* dummy = new ListNode(-1);
ListNode* cur = dummy;
while (h1 && h2) {
if (h1->val < h2->val) {
cur = cur->next = h1;
h1 = h1->next;
} else {
cur = cur->next = h2;
h2 = h2->next;
}
}
if (h1) cur->next = h1;
if (h2) cur->next = h2;
return dummy->next;
}
};
(迭代版归并排序)
如果想要实现空间复杂度为O(1)的话,则只能使用迭代版的归并排序。
迭代版的归并排序就是模拟递归自底向上的归并小区间中的链表。
迭代版的归并排序的难点在于:如何将小区间合并后,找到下一个小区间并且将其合并。
1.我们首先在外循环中循环区间的长度。
2.接着我们需要找到小区间,我们可以是实现一个split()函数,可以将一个链表的头结点后的step个节点分割成一个小链表并且返回下一个链表的头结点。
我们利用l1 = cur, l2 = split(l1, i), nextHead = split(l2, i)将链表分割成以l1, l2为头结点的链表,并且知道下一次需要分割的链表的头结点为nextHead。知道了两个小链表,我们只需要将两个链表合并即可。
class Solution {
public:
ListNode* split(ListNode* h, int step) {
if (!h) return h;
// 找到长度为step的h链表的尾节点,并将链表断开,返回下一个链表的头结点
ListNode* cur = h;
for (int i = 1; i < step && cur->next; i ++) cur = cur->next;
ListNode* nextHead = cur->next;
cur->next = nullptr;
return nextHead;
}
ListNode* sortList(ListNode* head) {
if (!head || !head->next) return head;
int n = 0;
for (ListNode* cur = head; cur; cur = cur->next) n ++;
ListNode* dummy = new ListNode(-1);
dummy->next = head;
for (int i = 1; i < n; i *= 2) { // 合并链表区间的长度
ListNode* prev = dummy, *cur = dummy->next;
while (cur) {
ListNode* l1 = cur;
ListNode* l2 = split(l1, i);
ListNode* nextHead = split(l2, i);
// 合并链表
while (l1 && l2) {
if (l1->val < l2->val) {
prev = prev->next = l1;
l1 = l1->next;
} else {
prev = prev->next = l2;
l2 = l2->next;
}
}
if (l1) prev->next = l1;
if (l2) prev->next = l2;
while (prev->next) prev = prev->next;
// cur更新为下一段合并链表的头结点
cur = nextHead;
}
}
return dummy->next;
}
};
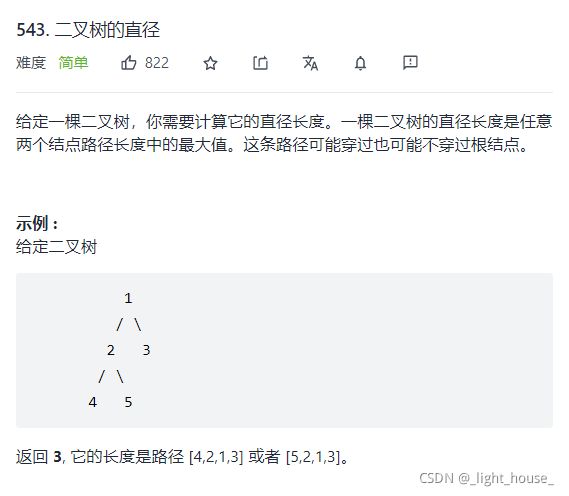
543. 二叉树的直径
(递归)
本题和「二叉树的最大路径和」很像。我们需要求出穿过root的最大直径,那么我们就需要知道root->left这个左子树上最深位置的路径上的节点个数和root->right右子树上最深位置的路径上的节点个数。而答案就是的能穿过所有节点中最大路径长度就是left + right。
为什么一定需要定义成穿过root节点的路径呢?
这是因为我们从root节点出发,所以需要递归函数和root节点产生关系,否则的话,左右子树都是独立的存在也就意味着所有的节点都是独立的存在。而因为需要求出一棵树的最长的路径,所以需要以某一个节点出发计算所有左右子树的最大贡献路径数,这样就可以让整个树连接起来了。
class Solution {
public:
int ans = INT_MIN;
int count(TreeNode* root) {
if (!root) return 0;
int left = count(root->left);
int right = count(root->right);
ans = max(ans, left + right);
return max(left, right) + 1;
}
int diameterOfBinaryTree(TreeNode* root) {
if (!root) return 0;
count(root);
return ans;
}
};
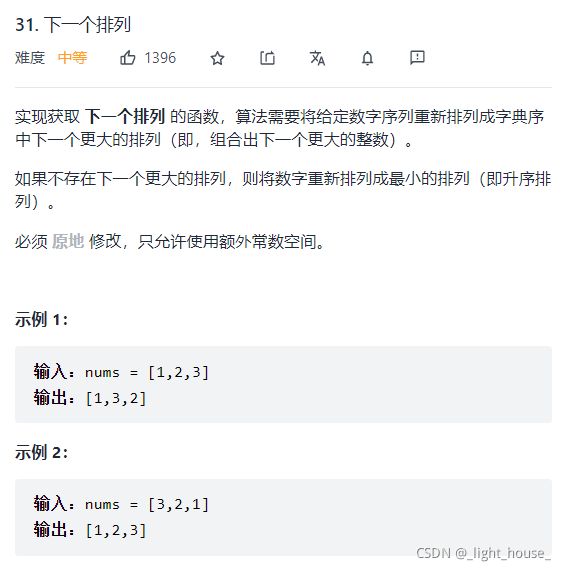
31. 下一个排列
(脑力+全排列)
class Solution {
public:
void nextPermutation(vector<int>& nums) {
int n = nums.size();
int k = n - 1;
while (k > 0 && nums[k] <= nums[k - 1]) k --;
if (k == 0) {
// 如果是降序的序列的话,则已经是全排列的最后一组数字了
reverse(nums.begin(), nums.end());
} else {
// 找到第一个比nums[k-1]大的数字
int index = k;
while (index < n && nums[index] > nums[k - 1]) index ++;
swap(nums[index - 1], nums[k - 1]);
reverse(nums.begin() + k, nums.end());
}
}
};
32. 最长有效括号
因为需要求出有效的子串,所以最暴力的方法应该是枚举所有的子串,然后判断子串的合法性即可。但是这样的时间复杂度为O(n3),所以会超时。
(栈)
我们知道栈对于这种相邻括号的处理具有天然的优势,所以可以考虑使用栈来解决这个问题。
做法:遍历整个字符串,因为以左括号为右端点不可能为有效的字符串,所以只有遇到右括号的时候,我们需要判断以当前为右括号的子串最长的合法序列的左端在什么位置上。
我们需要准备一个栈,用于存放左括号的下标,每当遇到一个右括号的时候,就可以让这个右括号和栈中的左括号匹配形成一对合法的序列。并且可以使用当前右括号的下标和栈中左括号的下标计算出合法序列的长度。
注意的细节:
1.当我们计算合法序列的长度的时候,我们需要使用当前的位置减去合法序列的左端的左边一个位置,而不是合法序列的最左端。这是因为((()))这种嵌套型的括号中,可以使用右端点减去左端点计算。但是如果是()()()这种相互独立的括号的话,就必须使用左端点的左边一个位置来计算了。
2.如果使用左端点没有左边怎么?
第一种:
1.我们可以在stack中手动的添加一个-1说明是第一个位置的左边一个位置。
2.而且如果遇到了一个右括号,同时栈中没有元素,说明此时当前的这个右括号不能形成合法的序列,所以我们让右括号作为两段独立的有效序列的中间产物,即这个右括号可以作为下一个有序序列的左端点的左边一个位置。如)(())。
第二种:
我们可以使用start变量记录下每一段有效序列的左端点。
如果遇到一个不能匹配的单独的一个右括号的时候,我们就更新一下start = i + 1,说明下一段有效序列的左端点一定在当前右括号的右边一个位置上。
当枚举到一段有效序列的左端点的是,因为没有左边一个位置了,所以可以使用i - start + 1来计算有效序列的长度。
class Solution {
public:
int longestValidParentheses(string s) {
int n = s.size();
stack<int> sk;
int ans = 0;
sk.push(-1); // 第一个位置的左边一个位置的下标为-1
for (int i = 0; i < n; i ++) {
if (s[i] == '(') {
sk.push(i);
} else {
sk.pop();
if (!sk.empty()) {
ans = max(ans, i - sk.top());
} else { // 右括号的下标作为分隔符
sk.push(i);
}
}
}
return ans;
}
};
class Solution {
public:
int longestValidParentheses(string s) {
int n = s.size();
stack<int> sk;
int ans = 0;
for (int i = 0, start = 0; i < n; i ++) {
if (s[i] == '(') {
sk.push(i);
} else {
if (!sk.empty()) {
sk.pop();
if (!sk.empty()) { // 可以使用左边一个位置直接计算
ans = max(ans, i - sk.top());
} else { // 使用start计算序列长度
ans = max(ans, i - start + 1);
}
} else {
// 更新分割点
start = i + 1;
}
}
}
return ans;
}
};
(正向逆向法)
对于只有一种类型的括号组成的括号序列判断器合法性,只需要满足两个性质即可:
1.左括号数量等于右括号数量。
2.任意一段序列前缀中,左括号的数量都大于等于右括号的数量。
所以我们只需要从前往后计算出左右括号的数量即可,当左右括号的数量相等的时候,更新一下答案即可。如果右括号的数量大于左括号的数量就重置左右括号的数量。
但是只有当左右括号数量相同的时候才可以计算。所以遇到()((())就不能将后面的合法序列计算出来。因此还需要从后往前在计算一遍。从后往前计算方法同理。
最后答案就是两种遍历方法的最大值。
class Solution {
public:
int longestValidParentheses(string s) {
int n = s.size();
int l = 0, r = 0;
int ans = 0;
for (int i = 0; i < n; i ++) {
if (s[i] == '(') l ++;
else r ++;
// 左括号已经不够匹配右括号了
if (r > l) l = 0, r = 0;
if (l == r) ans = max(ans, l * 2);
}
l = 0, r = 0;
for (int i = n - 1; i >= 0; i --) {
if (s[i] == '(') l ++;
else r ++;
// 右括号已经不够匹配左括号了
if (l > r) l = 0, r = 0;
if (l == r) ans = max(ans, l * 2);
}
return ans;
}
};
(动规)
本题可以看看是否有这个问题的子问题来判断是否可以使用动态规划。
一般情况下,如果题目中有「计数, 最大/最小/最长/最短,是够存在」等字眼,判断是否可以使用动态规划来解决,如果可以找到这个问题的子问题的话就可以使用动态规划来解决这个问题。
1.状态定义
dp[i]表示以第i个字符为结尾的最长有效子串的长度。
2.递推公式
s[i] == ‘(’一定不能构成以(为结尾的合法序列,所以dp[i] = 0s[i] == ‘)’因为是合法子串,所以dp[i]需要对s[i - 1]分情况s[i - 1] == ‘(’说明s[i]可以和s[i - 1]进行匹配,所以dp[i] = dp[i - 2] + 2s[i - 1] == ‘)’说明s[i]不可以和s[i - 1]进行匹配,但是需要看s[i - 1]是否为一段合法序列的右端点s[i - 1]是前面一段合法序列的右端点,dp[i - 1]为s[i - 1]合法序列的长度,所以如果s[i - dp[i - 1] - 1]为(的话,那么s[i]这个‘)’就可以和前面的左括号匹配在一起了。所以dp[i] = dp[i - 1] + 2 + dp[i - dp[i - 1] + 2]。但是如果i - dp[i - 1] + 2 < 0的话,那么dp[i] = dp[i - 1] + 2s[i - 1]就只是一段不合法的序列,那么s[i]就是一个不合法的序列,dp[i] = 0
虽然状态转移方程为dp[i] = dp[i - 2] + 2和dp[i] = 2 + dp[i - 1] + dp[i - dp[i - 1] - 2],但是如果我们恰好枚举到了以0下标为左端点的有效序列的话,那么i - 2 < 0并且i - dp[i - 1] - 2 < 0,所以递推公式为dp[i] = 2和dp[i] = 2 + dp[i - 2] + dp[i - dp[i - 1] + 2]
class Solution {
public:
int longestValidParentheses(string s) {
if (s.empty()) return 0;
int n = s.size();
vector<int> dp(n);
dp[0] = 0;
int ans = 0;
for (int i = 1; i < n; i ++) {
if (s[i] == ')') {
if (s[i - 1] == '(') {
if (i >= 2)
dp[i] = dp[i - 2] + 2;
else
dp[i] = 2;
}
if (s[i - 1] == ')') {
if (i - dp[i - 1] - 1 >= 0 && s[i - dp[i - 1] - 1] == '(') {
if (i - dp[i - 1] - 2 >= 0)
dp[i] = 2 + dp[i - 1] + dp[i - dp[i - 1] - 2];
else
dp[i] = 2 + dp[i - 1];
}
}
}
ans = max(ans, dp[i]);
}
return ans;
}
};
234. 回文链表
最简单的方式就是将链表放在一个数组中,然后利用双指针判断存在数组中的链表是否回文。
(反转链表)
如果想要使用O(1)的空间来判断的话,就必须使用双指针来判断。但是单链表又不能反向移动,所以我们就可以将链表的后半段反转一下形成一个新的链表,这样就可以使用双指针,从两个链表的开头判断是否两个链表相同。
核心思想:逆置链表达到可以从后往前遍历链表的目的。
做法:
1.使用快慢指针将链表分成两半(也可以计算链表的个数)
2.反转后半部分的链表
3.双指针判断
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* cur = head, *newHead = nullptr;
while (cur) {
ListNode* next = cur->next;
cur->next = newHead;
newHead = cur;
cur = next;
}
return newHead;
}
bool isPalindrome(ListNode* head) {
if (!head->next) return true;
// 快慢指针找中点
ListNode* fast = head, *slow = head;
ListNode* prev = head;
while (fast && fast->next) {
fast = fast->next->next;
prev = slow;
slow = slow->next;
}
// 断开链表
prev->next = nullptr;
ListNode* newHead = reverseList(slow);
ListNode* tail = newHead;
while (newHead && head) {
if (newHead->val != head->val) return false;
newHead = newHead->next;
head = head->next;
}
// 恢复链表
prev->next = reverseList(tail);
return true;
}
};
53. 最大子序和
(动规)
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int n = nums.size();
vector<int> dp(n);
int ans = INT_MIN;
for (int i = 0; i < n; i ++) {
dp[i] = nums[i];
if (i > 0) dp[i] = max(dp[i], dp[i - 1] + nums[i]);
ans = max(ans, dp[i]);
}
return ans;
}
};
(贪心)
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int n = nums.size();
int sum = 0;
int ans = INT_MIN;
for (int i = 0; i < n; i ++) {
if (sum > 0) sum += nums[i];
else sum = nums[i];
ans = max(ans, sum);
}
return ans;
}
};
322. 零钱兑换
(动规)
class Solution {
public:
const int INF = 0x3f3f3f3f;
int coinChange(vector<int>& coins, int amount) {
int n = coins.size();
vector<vector<int>> dp(n + 1, vector<int>(amount + 1, INF));
for (int i = 0; i <= n; i ++) dp[i][0] = 0;
for (int i = 1; i <= n; i ++) {
for (int j = 1; j <= amount; j ++) {
dp[i][j] = dp[i - 1][j];
if (j >= coins[i - 1]) {
dp[i][j] = min(dp[i][j], dp[i][j - coins[i - 1]] + 1);
}
}
}
if (dp[n][amount] == INF) return -1;
else return dp[n][amount];
}
};
(动规-一维空间优化)
class Solution {
public:
const int INF = 0x3f3f3f3f;
int coinChange(vector<int>& coins, int amount) {
int n = coins.size();
vector<int> dp(amount + 1, INF);
dp[0] = 0;
for (int i = 1; i <= n; i ++) {
for (int j = coins[i - 1]; j <= amount; j ++) {
dp[j] = min(dp[j], dp[j - coins[i - 1]] + 1);
}
}
if (dp[amount] == INF) return -1;
else return dp[amount];
}
};
39. 组合总和
(排序优化+爆搜)
排列问题用vis数组,避免重复使用同一个数字。组合问题用start变量,避免使用前面使用过的变量
class Solution {
public:
vector<vector<int>> ans;
vector<int> path;
void dfs(vector<int>& nums, int target, int start) {
if (target <= 0) {
if (target == 0) ans.push_back(path);
return ;
}
int n = nums.size();
for (int i = start; i < n; i ++) {
if (target - nums[i] < 0) continue;
path.push_back(nums[i]);
dfs(nums, target - nums[i], i);
path.pop_back();
}
}
vector<vector<int>> combinationSum(vector<int>& nums, int target) {
sort(nums.begin(), nums.end());
int n = nums.size();
dfs(nums, target, 0);
return ans;
}
};
35. 搜索插入位置
(二分)
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int n = nums.size();
if (target > nums.back()) return n;
int l = 0, r = n - 1;
while (l < r) {
int mid = l + r >> 1;
if (nums[mid] >= target) r = mid;
else l = mid + 1;
}
return l;
}
};
283. 移动零
(下标索引双指针)
使用两个指针,一个指针index控制0存储的位置,一个指针i遍历整个数组。只要遇到一个非零数就和index指向0的位置交换即可。
class Solution {
public:
void moveZeroes(vector<int>& nums) {
int n = nums.size();
int index = 0;
for (int i = 0; i < n; i ++) {
if (nums[i]) {
swap(nums[i], nums[index ++]);
}
}
}
};
165. 比较版本号
(双指针)
可以使用双指针将.之间的字符都抠出来,然后将抠出的两个字符串转化为数字比较一下即可。
class Solution {
public:
int compareVersion(string version1, string version2) {
int n = version1.size(), m = version2.size();
int i = 0, j = 0;
while (i < n || j < m) {
int v1 = 0, v2 = 0;
int k = i;
while (k < n && version1[k] != '.') k ++;
if (i <= n) v1 = stoi(version1.substr(i, k - i));
i = k + 1;
k = j;
while (k < m && version2[k] != '.') k ++;
if (j <= m) v2 = stoi(version2.substr(j, k - j));
j = k + 1;
if (v1 > v2) return 1;
if (v1 < v2) return -1;
}
return 0;
}
};
剑指 Offer 04. 二维数组中的查找
(找规律)
class Solution {
public:
bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
int n = matrix.size();
if (!n) return false;
int m = matrix[0].size();
int x = 0, y = m - 1;
while (x < n && y >= 0) {
if (matrix[x][y] < target) x ++;
else if (matrix[x][y] > target) y --;
else return true;
}
return false;
}
};
面试题 17.24. 最大子矩阵
(二维最大子序和)
本题其实一个最大子序和的问题,前面我们讲过「最大子序和」问题可以使用动规或者贪心来做。而本题就可以将二维的子矩阵和问题转换为一维的子数组和问题。
我们可以将二维数组看成一个比较“厚”的一维数组。而其中的子矩阵就可以看成一维的子数组。如果这样看的话就可以将二维子矩阵问题看成一维的子序和问题了。
为了枚举出所有子矩阵合成为一个子数组,所以我们需要两层循环。外面一层循环枚举需要合并子数组的头一行,而第二层循环就枚举需要合并子数组的尾一行。中间使用nums数组将二维的子数组中的同一列的数值相加起来就相当于合并二维数组了。
最后我们可以再贪心的方法求出合并后的子数组的最大子序和。并且使用ans记录先子矩阵的左上角和右下角。注意:第二层循环的变量和第三层循环的变量就是子矩阵的右下角的坐标。而第一层循环变量就是子矩阵的左上角的横坐标。而左上角的纵坐标需要我们自己记录下来。
class Solution {
public:
vector<int> getMaxMatrix(vector<vector<int>>& matrix) {
int n = matrix.size(), m = matrix[0].size();
int sum = INT_MIN;
vector<int> ans(4, -1);
for (int i = 0; i < n; i ++) {
vector<int> nums(m);
for (int j = i; j < n; j ++) {
// 求出最大子序和
int dp = 0, start = -1;
for (int k = 0; k < m; k ++) {
nums[k] += matrix[j][k];
if (dp > 0) {
dp += nums[k];
} else {
dp = nums[k];
start = k;
}
if (dp > sum) {
sum = dp;
ans[0] = i;
ans[1] = start;
ans[2] = j;
ans[3] = k;
}
}
}
}
return ans;
}
};
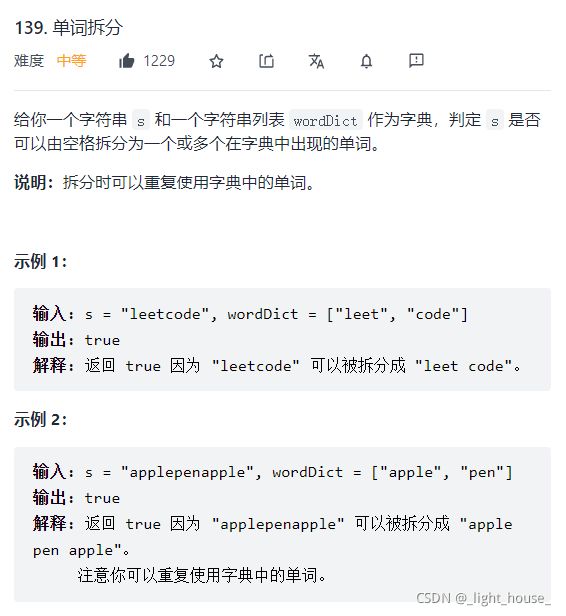
139. 单词拆分
(动规)
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
unordered_set<string> hash;
for (auto& str : wordDict) hash.insert(str);
int n = s.size();
vector<bool> dp(n + 1);
dp[0] = true;
s = ' ' + s;
for (int i = 1; i <= n; i ++) {
for (int j = 1; j <= i; j ++) {
if (hash.count(s.substr(j, i - j + 1))) {
dp[i] = dp[i] | dp[j - 1];
}
}
}
return dp[n];
}
};
(字符串哈希+动规)
因为hash.count(str)的时间是和str.size()有关系的,所以如果str很长的话,hash.count()就不是O(1)的了,而是O(n)的。
所以可以手动的将字符串哈希一下,即将字符串转化为一个P进制的数字。根据秦九韶算法的原理,可以遍历一遍字符串通过公式t = t * P + ch即可算出。(注意:其中的P一般取131或者1331,这样就可以使得哈希值不会冲突。并且t要使用unsigned long long来保存,这样就可以做到如果数字过大的时候,数字溢出就相当于对于264取模了)这样就可以将hash.count()的时间复杂度降为O(1)了。
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
typedef unsigned long long ULL;
const int P = 131;
unordered_set<ULL> hash;
for (auto& word : wordDict) {
ULL t = 0;
for (auto ch : word) t = t * P + ch;
hash.insert(t);
}
int n = s.size();
vector<bool> dp(n + 1);
dp[0] = true;
s = ' ' + s;
for (int i = 0; i < n; i ++) {
if (dp[i]) {
ULL t = 0;
for (int j = i + 1; j <= n; j ++) {
t = t * P + s[j];
if (hash.count(t)) dp[j] = true;
}
}
}
return dp[n];
}
};
(字符串哈希(反向)+动规)
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
typedef unsigned long long ULL;
const int P = 131;
unordered_set<ULL> hash;
for (auto& word : wordDict) {
ULL t = 0;
for (char c : word) t = t * P + c;
hash.insert(t);
}
int n = s.size();
vector<bool> dp(n + 1);
dp[n] = true;
for (int i = n - 1; i >= 0; i --) {
ULL t = 0;
for (int j = i; j < n; j ++) {
t = t * P + s[j];
if (hash.count(t)) dp[i] = dp[i] | dp[j + 1];
}
}
return dp[0];
}
};
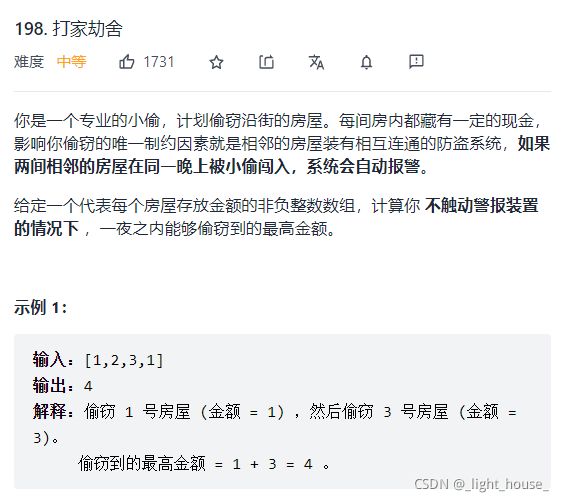
198. 打家劫舍
(动规)
class Solution {
public:
int rob(vector<int>& nums) {
int n = nums.size();
vector<vector<int>> dp(n + 1, vector<int>(2));
for (int i = 1; i <= n; i ++) {
dp[i][0] = max(dp[i - 1][1], dp[i - 1][0]);
dp[i][1] = dp[i - 1][0] + nums[i - 1];
}
return max(dp[n][0], dp[n][1]);
}
};
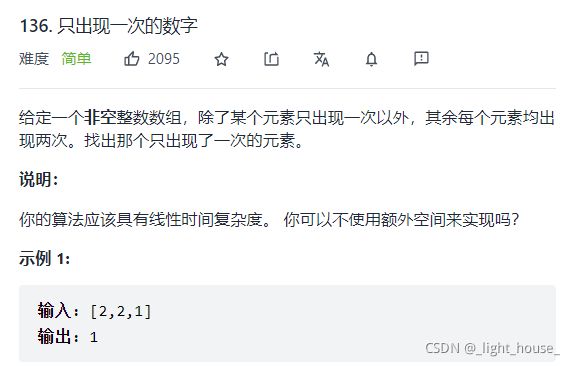
136. 只出现一次的数字
(异或运算)
class Solution {
public:
int singleNumber(vector<int>& nums) {
int ans = 0;
for (int num : nums) {
ans ^= num;
}
return ans;
}
};
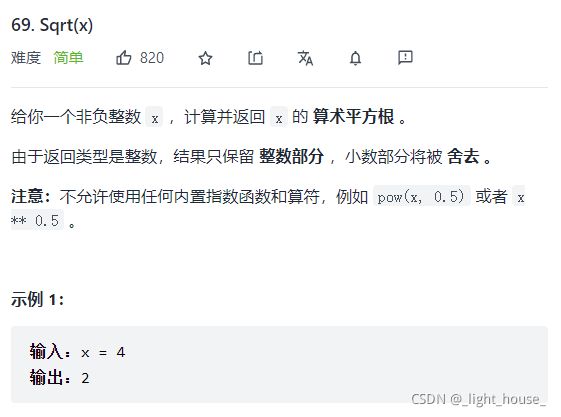
69. Sqrt(x)
(二分)
我们要找出一个数字的算术平方根,并且不能带有小数部分。那么其实就是要找出小于等于x的最大正整数。
如果将题目转化为在一个有序数组中找出<=x的最大正整数,直接使用二分的模板即可。
注意:因为x有可能是INT_MAX,所以如果使用int类型的l和r的话,当计算mid = l + (r - l + 1) / 2的时候,就会因为INT_MAX + 1而爆int。
所以针对这种情况,有两种方法可以解决:
1.可以使用long long来保存r和l,long long的范围很大就不会发生溢出问题了。
2.可以使用mid = l + 1ll + r >> 1,其中1ll表示long long类型的1,通过这样就可以使得l + 1ll + r在计算的时候为long long类型了。然后将long long类型的数字赋值给int进行截断。
class Solution {
public:
int mySqrt(int x) {
int l = 0, r = x;
while (l < r) {
// 这里强转一下即可
// 或者可以使用longlong的l和r,然后mid=l+(r-l+1)/2
int mid = l + 1ll + r >> 1;
if (mid <= x / mid) l = mid;
else r = mid - 1;
}
return l;
}
};
26. 删除有序数组中的重复项
(双指针)
对于有序数组的去重是相对简单的,因为有序数组中重复的元素已经是连续的了。所以我们就可以通过找到每一段相同的连续数字的开头或者结尾将重复元素单独挑出来。
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
int n = nums.size();
int index = 0;
// 找出每一段连续相同的数字的最后一个数字,让在index位置上,然后index++
for (int i = 0; i < n; i ++) {
int j = i;
while (j + 1 < n && nums[j] == nums[j + 1]) j ++;
nums[index ++] = nums[j];
i = j;
}
return index;
}
};
(双指针2)
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
int n = nums.size();
int index = 0;
for (int i = 0; i < n; i ++) {
// 找到每一段连续相同的数字的第一个数字,放在index位置上,然后index++
// 第一个数字不用找,nums[index] = nums[0]
if (!i) {
nums[index ++] = nums[i];
continue;
}
int j = i;
while (j < n && nums[j] == nums[j - 1]) j ++;
// 注意nums[j]不能越界
if (j != n) nums[index ++] = nums[j];
i = j;
}
return index;
}
};
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
int n = nums.size();
int index = 0;
for (int i = 0; i < n; i ++) {
// 如果是第一个数字或者是一段连续数字的第一个数字的话,就放在数组的前面
if (!i || nums[i] != nums[i - 1])
nums[index ++] = nums[i];
}
return index;
}
};
(库函数)
库函数中有一个unique函数是专门用来将有序数组中重复的元素放在数组的后面,而前面unique(nums.begin() - nums.end()) - nums.begin()个数字放在数组的前面。
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
return unique(nums.begin(), nums.end()) - nums.begin();
}
};
84. 柱状图中最大的矩形
(单调栈)
要找出柱状图中的最大值面积的话,就要知道矩形的面积怎么求?
如果我们枚举矩形的宽,那么就可以循环两层枚举出所有矩形的宽,并且在枚举宽的过程中计算矩形的面积。
如果我们枚举矩形的高,那么就需要以一个柱子为基准,找到以这个柱子为高的矩形的最大面积,所以就需要找到矩形的左右边界。因为就需要O(n)的去寻找左右边界,即离当前柱子最近的比这个柱子要低的柱子。这样的做法也是O(n2)的,但是需要找到左右两边最近的最低的位置可以使用单调栈来优化。
1.可以使用两个数组left和right保存单调栈计算出每一个位置左右两边的最近最小的位置的下标。
2.因为寻找右边最近最小的位置的下标,需要维护一个单调递增的栈。所以当找到右边最近最小的位置的时候,栈中栈顶下面的一个元素就是栈顶元素的左边界。
class Solution {
public:
int largestRectangleArea(vector<int>& nums) {
nums.push_back(0);
int n = nums.size();
stack<int> sk;
int ans = 0;
for (int i = 0; i < n; i ++) {
while (!sk.empty() && nums[i] < nums[sk.top()]) {
int top = sk.top();
sk.pop();
int w = 0;
if (sk.empty()) w = i;
else w = i - sk.top() - 1;
int h = nums[top];
ans = max(ans, w * h);
}
sk.push(i);
}
return ans;
}
};
(保存单调栈)
class Solution {
public:
int largestRectangleArea(vector<int>& nums) {
int n = nums.size();
stack<int> sk;
vector<int> left(n);
vector<int> right(n);
for (int i = 0; i < n; i ++) {
while (!sk.empty() && nums[sk.top()] >= nums[i]) sk.pop();
if (sk.empty()) left[i] = -1;
else left[i] = sk.top();
sk.push(i);
}
sk = stack<int>();
for (int i = n - 1; i >= 0; i --) {
while (!sk.empty() && nums[sk.top()] >= nums[i]) sk.pop();
if (sk.empty()) right[i] = n;
else right[i] = sk.top();
sk.push(i);
}
int ans = 0;
for (int i = 0; i < n; i ++)
ans = max(ans, nums[i] * (right[i] - left[i] - 1));
return ans;
}
};
278. 第一个错误的版本
(二分)
经典的二分,因为整个序列是有序的,并且有明确的二段性,即[1, i]中版本是true。而[i + 1, n]之间版本是false。所以需要快速地找到第一个错误版本就可以使用二分。
class Solution {
public:
int firstBadVersion(int n) {
int l = 1, r = n;
while (l < r) {
int mid = l + (r - l) / 2;
if (isBadVersion(mid)) r = mid;
else l = mid + 1;
}
return l;
}
};
105. 从前序与中序遍历序列构造二叉树
(哈希表+递归)
需要通过前中序列就构建出树,就需要划分出根节点,左子树,右子树。然后将三者连接起来既可以构建出一棵树了。
我们需要观察前序序列和中序序列的性质。我们知道因为前序序列从前往后的节点就是每一棵树的根,所以我们就可以通过前序序列找出子树的根节点,然后在中序序列中找到根节点的位置,这样就可以划分出根节点,左子树和右子树。
注意:使用哈希表可以只需要O(1)的时间就在中序遍历序列中找到根节点的位置,这样就可以不用O(n)的去查找根节点的位置了。
class Solution {
public:
unordered_map<int, int> hash;
TreeNode* build(vector<int>& preorder, int& rooti, vector<int>& inorder, int l, int r) {
if (l > r) return nullptr;
TreeNode* root = new TreeNode(preorder[rooti]);
int index = hash[root->val];
rooti ++;
root->left = build(preorder, rooti, inorder, l, index - 1);
root->right = build(preorder, rooti, inorder, index + 1, r);
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
int n = inorder.size();
for (int i = 0; i < n; i ++)
hash[inorder[i]] = i;
int rooti = 0;
return build(preorder, rooti, inorder, 0, n - 1);
}
};
106. 从中序与后序遍历序列构造二叉树
(哈希表定位+递归)
class Solution {
public:
unordered_map<int, int> hash;
TreeNode* build(vector<int>& postorder, int& rooti, vector<int>& inorder, int l, int r) {
if (l > r) return nullptr;
TreeNode* root = new TreeNode(postorder[rooti]);
rooti --;
int index = hash[root->val];
root->right = build(postorder, rooti, inorder, index + 1, r);
root->left = build(postorder, rooti, inorder, l, index - 1);
return root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
int n = inorder.size();
for (int i = 0; i < n; i ++)
hash[inorder[i]] = i;
int rooti = n - 1;
return build(postorder, rooti, inorder, 0, n - 1);
}
};
6. Z 字形变换
(找规律)
将Z型变换组成的图形对应的位置写成字符串的下标,就可以发现第一行和最后一行的规律在于相邻的两个数字的公差是2 * numRows - 2。而中间的row即1 <= row <= numRows - 1是由两个等差数列组成的。而且公差也是2 * numRow - 2。
所以可以利用这个规律,我们只需要一行一行的拼接字符串即可。
class Solution {
public:
string convert(string s, int numRows) {
if (numRows == 1) return s;
int n = s.size();
string ans;
int cycle = 2 * numRows - 2;
for (int i = 0; i < numRows; i ++) {
if (i == 0 || i == numRows - 1) {
for (int j = i; j < n; j += cycle)
ans += s[j];
} else {
for (int j = i, k = cycle - i; j < n || k < n; j += cycle, k += cycle) {
if (j < n) ans += s[j];
if (k < n) ans += s[k];
}
}
}
return ans;
}
};
(找规律2)
本题的第二个规律,就是利用偏移量来解决这个问题。
可以定义numRow个string,表示每一行的字符串,并将字符串拼接在每一行上(空格部分不算)。而我们在遍历整个字符串的时候,需要在第一行和最后一行变换移动的方向,所以需要使用一个变量down判断是否向下移动或者可以定义一个移动数字xd[2] = {1, -1}表示移动的方向。这样就可以将每一行的字符拼接在对应的rows[curRow]上了。
最后只需要将每一行的字符串都拼接起来即可。
class Solution {
public:
string convert(string s, int numRows) {
if (numRows == 1) return s;
int n = s.size();
int curRow = 0;
bool down = false;
vector<string> rows(numRows);
for (int i = 0; i < n; i ++) {
if (curRow == 0 || curRow == numRows - 1) down = !down;
rows[curRow] += s[i];
curRow += down ? 1 : -1;
}
string ans;
for (string& row : rows) ans += row;
return ans;
}
};
(找规律-蛇形矩阵)
class Solution {
public:
string convert(string s, int numRows) {
if (numRows == 1) return s;
int xd[2] = {1, -1};
int d = 0, x = 0;
int n = s.size();
vector<string> rows(numRows);
for (int i = 0; i < n; i ++) {
rows[x] += s[i];
// 先用a去试探一下是否越界
int a = x + xd[d];
if (a == numRows || a < 0) {
// 如果越界就改变方向
d = (d + 1) % 2;
a = x + xd[d];
}
x = a;
}
string ans;
for (string& row : rows) ans += row;
return ans;
}
};
179. 最大数
(贪心+排序)
本题就是在定义一个新的比较运算符,即a < b中的<的含义为ab < ba,其中a和b都是字符串,所以可以拼接在一起。
所以我们要做的就是将nums按上述的规律排序,最后拼接成一个字符串。
我们可以定义一个比较函数,比较n1和n2两个数字。因为需要比较拼接后的字符串,所以我们首先将n1和n2都转换成字符串。然后返回a + b > b + a即可。
class Solution {
public:
struct Cmp {
bool operator()(int n1, int n2) {
string a = to_string(n1);
string b = to_string(n2);
return a + b > b + a;
}
};
string largestNumber(vector<int>& nums) {
sort(nums.begin(), nums.end(), Cmp());
string ans;
for (auto num : nums) {
ans += to_string(num);
}
int k = 0, n = nums.size();
while (k < n - 1 && ans[k] == '0') k ++;
return ans.substr(k);
}
};
226. 翻转二叉树
(递归)
本题就是一个简单的递归的问题。我们如果想要反转整个一棵树,那么就需要先将左子树反转,然后将右子树反转。最后将root的左右孩子的指向改变一下方向即可。因为需要用到root->left和root->right所以我们的终止条件就是!root的时候,我们需要返回nullptr。
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if (!root) return nullptr;
TreeNode* left = invertTree(root->left);
TreeNode* right = invertTree(root->right);
root->left = right;
root->right = left;
return root;
}
};
剑指 Offer 10- II. 青蛙跳台阶问题
(动规)
class Solution {
public:
int numWays(int n) {
if (n == 0 || n == 1) return 1;
const int mod = 1e9 + 7;
vector<int> dp(n + 1);
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= n; i ++) {
dp[i] = (dp[i - 1] + dp[i - 2]) % mod;
}
return dp[n];
}
};
(完全背包解法)
class Solution {
public:
int numWays(int n) {
if (n == 0 || n == 1) return 1;
const int mod = 1e9 + 7;
vector<int> nums = {1, 2};
vector<int> dp(n + 1);
dp[0] = 1;
for (int i = 1; i <= n; i ++)
for (int j = 0; j < 2; j ++)
if (i >= nums[j])
dp[i] = (dp[i] + dp[i - nums[j]]) % mod;
return dp[n];
}
};
进阶问题(变态青蛙跳台阶)
(找规律)
我们可以发现:
f(1) = 1;
f(2) = f(1) + 1 = 2
f(3) = f(2) + f(1) + 1 = 2 + 1 + 1 = 4;
f(4) = f(3) + f(2) + f(1) + 1 = 8;
...
f(n) = f(n - 1) + f(n - 2) + ... + f(1) + 1 = 2 * f(n - 1) = 2 ^ (n - 1);
所以,只需要返回2(n-1)即可,如果用位运算的话就是1 << (n - 1)。
class Solution {
public:
int jumpFloorII(int n) {
if (n == 0 || n == 1) return 1;
int ans = 1;
ans <<= n - 1;
return ans;
}
};
剑指 Offer 13. 机器人的运动范围
(dfs)
我们需要找到所以满足(x, y)坐标的数位之和大于k的格子。所以我们就是在寻找有某种性质的所有方块。这些方块组合而成的其实就是一个大的连通块。所以就可以使用dfs或者bfs就连通块的方式求解出连通块中的所有位置元素的个数即可。
class Solution {
public:
int xd[4] = {0, 1, 0, -1};
int yd[4] = {1, 0, -1, 0};
int ans = 0;
bool isvaild(int x, int y, int k) {
int t = 0;
while (x) {
t += x % 10; x /= 10;
}
if (t > k) return false;
while (y) {
t += y % 10; y /= 10;
}
if (t > k) return false;
return true;
}
void dfs(int x, int y, int k, vector<vector<bool>>& vis) {
vis[x][y] = true;
ans ++;
int n = vis.size(), m = vis[0].size();
for (int i = 0; i < 4; i ++) {
int xi = x + xd[i], yi = y + yd[i];
if (xi < 0 || yi < 0 || xi >= n || yi >= m ||
vis[xi][yi] || !isvaild(xi, yi, k)) continue;
dfs(xi, yi, k, vis);
}
}
int movingCount(int m, int n, int k) {
vector<vector<bool>> vis(m, vector<bool>(n));
dfs(0, 0, k, vis);
return ans;
}
};
(bfs)
class Solution {
public:
bool isVailed(int x, int y, int k) {
int t = 0;
while (x) {
t += x % 10; x /= 10;
}
if (t > k) return false;
while (y) {
t += y % 10; y /= 10;
}
if (t > k) return false;
return true;
}
typedef pair<int, int> PII;
int movingCount(int m, int n, int k) {
vector<vector<bool>> vis(m, vector<bool>(n));
queue<PII> q;
q.push({0, 0});
int ans = 0;
int xd[4] = {0, 1, 0, -1}, yd[4] = {1, 0, -1, 0};
while (!q.empty()) {
auto top = q.front();
q.pop();
int x = top.first, y = top.second;
vis[x][y] = true;
if (!isVailed(x, y, k)) return ans;
ans ++;
for (int i = 0; i < 4; i ++) {
int xi = x + xd[i], yi = y + yd[i];
if (xi < 0 || yi < 0 || xi >= m || yi >= n ||
vis[xi][yi] || !isVailed(xi, yi, k)) continue;
vis[xi][yi] = true;
q.push({xi, yi});
}
}
return ans;
}
};
剑指 Offer 06. 从尾到头打印链表
(栈)
class Solution {
public:
vector<int> reversePrint(ListNode* head) {
ListNode* cur = head;
stack<int> sk;
while (cur) {
sk.push(cur->val);
cur = cur->next;
}
vector<int> ans;
while (!sk.empty()) {
ans.push_back(sk.top());
sk.pop();
}
return ans;
}
};
(反转链表)
class Solution {
public:
vector<int> reversePrint(ListNode* head) {
ListNode* cur = head, *newHead = nullptr;
while (cur) {
ListNode* next = cur->next;
cur->next = newHead;
newHead = cur;
cur = next;
}
vector<int> ans;
while (newHead) {
ans.emplace_back(newHead->val);
newHead = newHead->next;
}
return ans;
}
};
(递归)
class Solution {
public:
vector<int> reversePrint(ListNode* head) {
if (!head) return {};
vector<int> ans = reversePrint(head->next);
ans.push_back(head->val);
return ans;
}
};
面试题 01.01. 判定字符是否唯一
面试中不需使用任何的高级数据结构。
(位运算)
如果字符串中只存在一种类型的字符的话,我们可以使用一个变量当做vector数组,也就是当做哈希表,查询是否存在重复的数字。
位运算中技巧:
1.flag & (1 << k)可以检查flag中从右向左数的第k个位置为0或者1。
2.falg | (1 << k)可以将flag中从右向左数的第k个位置替换成1。
通过上述的两种操作,就可以将flag的每一个比特位当做容量为32的bool数组使用了。
class Solution {
public:
bool isUnique(string astr) {
int flag = 0;
for (char ch : astr) {
int move = ch - 'a';
if (flag & (1 << move)) return false;
else flag = flag | (1 << move);
}
return true;
}
};
9. 回文数
(字符串+双指针)
class Solution {
public:
bool isPalindrome(int x) {
string s = to_string(x);
int l = 0, r = s.size() - 1;
while (l < r) {
if (s[l] == s[r]) l ++, r --;
else return false;
}
return true;
}
};
(快速写法)
class Solution {
public:
bool isPalindrome(int x) {
if (x < 0) return false;
string s = to_string(x); // 将x转换成字符串
return s == string(s.rbegin(), s.rend()); // 查看s和反转后的s是否相等
}
};
(整数反转)
class Solution {
public:
bool isPalindrome(int x) {
if (x < 0) return false;
int t = x;
int num = 0;
while (t) {
if (num > (INT_MAX - t % 10) / 10) return false;
num = num * 10 + t % 10;
t /= 10;
}
return num == x;
}
};
(反转半边)
class Solution {
public:
bool isPalindrome(int x) {
if (x < 0 || x && x % 10 == 0) return false;
int num = 0;
while (num <= x) {
num = num * 10 + x % 10;
if (x == num || x / 10 == num) return true;
x /= 10;
}
return false;
}
};
189. 轮转数组
(两次反转)
class Solution {
public:
void rotate(vector<int>& nums, int k) {
int n = nums.size();
k %= n;
reverse(nums.begin(), nums.end());
reverse(nums.begin(), nums.begin() + k);
reverse(nums.begin() + k, nums.end());
}
};
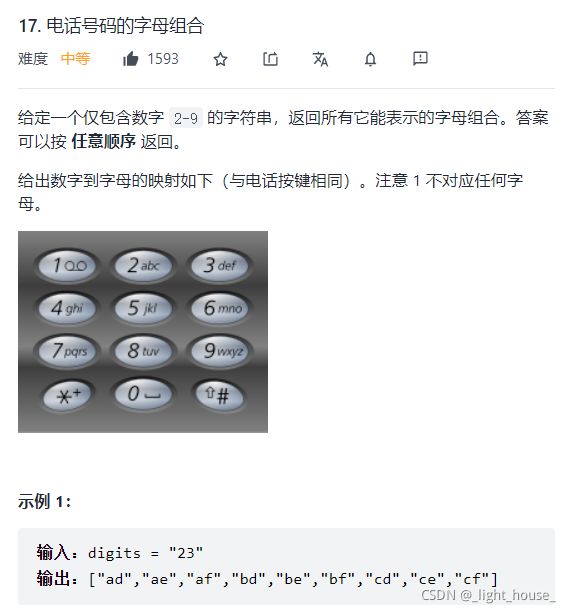
17. 电话号码的字母组合
(dfs-回溯)
本题就是一个简单的全排列问题。
每一个键盘数字都对应着不同的字符,我们需要找到所有不同键盘数字对应的字符全部拼接起来的不同组合。
所以我们可以从每一个数字对应的字符中选出一个字符,然后将digits.size()个字符拼接在一起就是一种组合的字符串,最后放入ans中即可。而这一个过程我们可以使用递归实现所有的不同组合。
补充:这题其实要比全排列还要简单。因为全排列是对于一个数字或者字符串的每一位进行递归,所以对于每一个数字可以会重复出现,我们还需要用一个哈希表或者bool数组判重。但是本题每一个需要组合的字符都存在与不同数字对应的字符串中,所以可以不用判重。
class Solution {
public:
vector<string> key = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
vector<string> ans;
string path;
void dfs(int index, string& digits) {
int n = digits.size();
if (index == n) {
ans.push_back(path);
return ;
}
string tele = key[digits[index] - '0'];
int len = tele.size();
for (int i = 0; i < len; i ++) {
path += tele[i];
dfs(index + 1, digits);
path.pop_back();
}
}
vector<string> letterCombinations(string digits) {
if (digits.empty()) return ans;
dfs(0, digits);
return ans;
}
};
剑指 Offer 40. 最小的k个数
(小根堆)
class Solution {
public:
vector<int> getLeastNumbers(vector<int>& arr, int k) {
priority_queue<int> q;
int n = arr.size();
for (int i = 0; i < n; i ++) {
q.push(arr[i]);
if (q.size() > k) q.pop();
}
vector<int> ans;
while (!q.empty()) {
ans.push_back(q.top());
q.pop();
}
return ans;
}
};
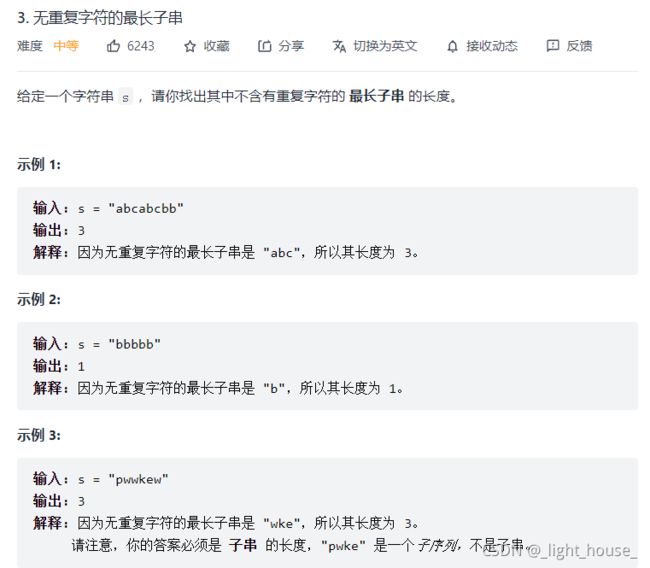
3.无重复字符的最长子串
(双指针 + 滑动窗口)
一个长度为n的字符串的子串有n2级别的个数,所以如果想要枚举出所有的子串那么一定会超时。
经过观察我们可以发现不含重复子串的子串具单调性,即如果[2, 4]范围的子串中没有重复的字符,那么要观察[2, 5]范围内是够具有重复的字符只需要查看s[5]是否在[2, 4]内出现过即可,而不需要判断s[5]是否在[0, 1]的范围内出现过。因为如果[1, 5]中都没有重复的字符的话,那么[1, 4]中也应该没有重复的字符,这就和前面[2, 4]的范围中没有重复的字符矛盾了。
因为我们判断子串只需要往后面的字符串判断是否出现重复字符,所以我们可以使用双指针算法来解决。
并且为了可以在O(1)的时间内,判断一段字符串中是否有重复的字符出现,我们可以使用哈希表来存储字符。
总体思路:将滑动窗口的右指针向右移动,将字符包含进窗口。如果一旦发现进入窗口的字符已经在窗口中出现的时候,我们就缩紧左窗口,也就是将左指针的指向字符踢出窗口中,并且左指针也向右移动。答案即使每一次窗口的大小。
class Solution {
public:
int lengthOfLongestSubstring(string s) {
unordered_map<char, int> hash;
int n = s.size();
int ans = 0;
int l = 0;
for (int r = 0; r < n; r ++) {
if (!hash.count(s[r])) {
hash[s[r]] ++;
} else {
while (hash.count(s[r])) { // 一直缩紧到窗口中没有重复字符为止
hash.erase(s[l]);
l ++;
}
hash[s[r]] ++;
}
ans = max(ans, j - i + 1);
}
return ans;
}
};
// 2021年10月12日 zhy
(滑动窗口简洁版)
同样的思路,我们可以换一种写法。
上面一种写法使用hash.count()来对字符是否在哈希表中来分情况讨论的。
其实我们可以默认将右窗口一直扩张,如果发现刚加入的字符已经重复的话,我们才缩紧左窗口,直到刚加入的字符在窗口中已经不重复为止。
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int n = s.size();
unordered_map<char, int> hash;
int l = 0;
int ans = 0;
for (int r = 0; r < n; r ++) {
hash[s[r]] ++;
while (hash[s[r]] > 1) hash[s[l ++]] --;
ans = max(ans, r - l + 1);
}
return ans;
}
};
// 2021年10月12日 zhy
5.最长回文子串
对于怎么判断一个回文串,有两种方法。
第一种方法就是从一段字符串的两端往内判断是否对应位置上的字符相同,如果全部相同,则字符串为回文串。
第二种方法就是从一段字符串的中心开始判断(如果字符串中的字符个数为偶数个,那么中心的个数为中间对称的两个位置;如果字符串中字符的个数为奇数个,那么字符换中心的个数就是字符串中间位置的哪一个字符),然后外延伸判断。
总的来说:其实中心判断要比从字符串的两端判断要好,虽然这两种的方法时间复杂度都是为O(n2)的,但是其实如果使用第一种方法,那么就一定需要判断所有的字符串,而第二种方法在判断的过程中,如果发现不能形成回文串就直接舍弃掉了很多以同样字符为中心的字符串,这样效率很大大的提升。
(动规)
最典型的区间DP,一般处理回文串的问题都是考虑一段区间中的字符串的问题,而一段大区间又可以用很多段小区间所转移,所以可以使用区间DP来解决问题。
并且dp数组中装的不是最长的回文串,而是判断字符串是否为回文串,因为只有判断一个字符串是否为回文串才可以转移。而字符串本身是不可以转移的。
1.状态定义
dp[i][j]表示:在[i, j]区间内的字符串是否为回文子串。
2.递推公式
更具回文串的两端来判断。
只有s[i] == s[j]的时候,才可能会是回文串。如果s[i] == s[j]的话,[i, j]范围中的字符串是否回文就取决于[i + 1, j - 1]中的字符串是否回文。所以dp[i][j] = dp[i + 1][j - 1]。
2.初始化
当s[i] == s[j]的时候,并且len <= 2时,那么[i, j]范围中的字符串一定是回文串。所以满足这种情况的所有字符串都是回文串,所以dp[i][j] = true
4.遍历顺序
一般情况下,区间DP的循环都是枚举区间的两个端点,但是还有一种等价的循环方式是,外循环区间的长度,内循环区间的左端点,然后通过左端点的位置和区间的长度来计算出右端点,而不是循环右端点,这样循环比较通用。
class Solution {
public:
string longestPalindrome(string s) {
int n = s.size();
string ans;
vector<vector<bool>> dp(n, vector<bool>(n));
for (int len = 1; len <= n; len ++) {
for (int i = 0; i + len - 1 < n; i ++) {
int j = i + len - 1;
if (s[i] == s[j]) {
if (len < 3) dp[i][j] = true;
else dp[i][j] = dp[i + 1][j - 1];
}
if (dp[i][j] && ans.size() < len) {
ans = s.substr(i, len);
}
}
}
return ans;
}
};
(中心扩展法)
第二种方法就是通过枚举字符串的中心,向外判断以该当前位置为中心的字符串是否为回文串。
class Solution {
public:
string longestPalindrome(string s) {
int n = s.size();
string ans;
for (int i = 0; i < n; i ++) {
int l = i, r = i;
while (l >= 0 && r < n && s[l] == s[r]) l --, r ++;
// 如果此时的l和r都已经是不满足条件的l和r了,满足条件的l和r是l+1和r-1
if (r - l - 1 > ans.size()) {
ans = s.substr(l + 1, r - l - 1);
}
l = i, r = i + 1;
while (l >= 0 && r < n && s[l] == s[r]) l --, r ++;
if (r - l - 1 > ans.size()) {
ans = s.substr(l + 1, r - l - 1);
}
}
return ans;
}
};
7.整数反转
(数字处理)
本题就是一个简单的数字处理问题,但是要注意的是如果一个数字翻转之后超过了int的范围的话,就直接return 0。所以对于数字只能使用int范围的数字,所以不能使用long long来保存数字,也就是ans * 10 + x % 10 > INT_MAX和ans * 10 + x % 10 < INT_MIN都是不可以的。因为ans * 10 + x % 10会超出范围,所以可以做一个等价的变形,即ans > (INT_MAX - x % 10) / 10,这样就可以不用对ans做出处理了。
class Solution {
public:
int reverse(int x) {
int ans = 0;
while (x) {
if (x > 0 && ans > (INT_MAX - x % 10) / 10) return 0;
if (x < 0 && ans < (INT_MIN - x % 10) / 10) return 0;
ans = ans * 10 + x % 10;
x /= 10;
}
return ans;
}
};
8. 字符串转换整数 (atoi)
(字符串处理)
对于字符串需要进行4种不同的处理:
1.处理空格
可以使用一个变量直接跳过前面s[i] == ' '的部分,并且如果i == s.size()说明整个字符串都是空格可以直接return 0。
2.处理符号
使用一个变量记录字符串第一个符号为-还是+,但是要注意一个数字只有一个符号,所以如果出现-+12,那么第二个符号就是一个特殊符号,而遇到特殊符号的时候,就直接返回前面的结果。
3.转化数字ans = ans * 10 + s[i] - ‘0’
3.1.如果遇到了特殊符号,也就是非数字的符号,就直接返回前面计算的结果。
3.2.如果s[i]已经超出了int的范围的话,就发生截断,即ans > INT_MAX就直接返回INT_MAX。如果ans < INT_MIN就直接返回INT_MIN。但是要注意:因为我们是先将符号提出来的,所以ans存储的是数字的正数为,即若如果是一个负数,存储的数字也是除了负号之外的数字。而int最大为2147483647,而最小值为-2147483648,所以ans是不能存储2147483648的,所以如果遇到了-2147483648的时候,我们需要特殊判断一下,其余的情况,我们只需要使用上面的手法判断即可,即ans > (INT_MAX - tmp) / 10,负数同理。
但是其实也可以使用if (flag < 0 && ans > (INT_MAX + tmp) / 10)来判断,因为如果ans > (INT_MAX - tmp) / 10的话,那么ans就一定是>= INT_MIN,所以可以直接返回INT_MIN。
class Solution {
public:
int myAtoi(string s) {
int ans = 0;
int i = 0;
// 处理空格
while (i != s.size() && s[i] == ' ') i ++;
if (i == s.size()) return 0;
// 处理符号
int flag = 1;
if (s[i] == '-') flag *= -1, i ++;
else if (s[i] == '+') i ++;
// 转化成数字,直到遇到非数字,而且需要特判截断的情况
while (i < s.size() && s[i] <= '9' && s[i] >= '0') {
int tmp = s[i] - '0';
if (flag > 0 && ans > (INT_MAX - tmp) / 10) return INT_MAX;
// if (flag < 0 && ans > (INT_MAX - tmp) / 10) return INT_MIN;
if (flag < 0 && -ans < (INT_MIN + tmp) / 10) return INT_MIN;
if (-ans * 10 - tmp == INT_MIN) return INT_MIN;
ans = ans * 10 + tmp;
i ++;
}
return ans * flag;
}
};