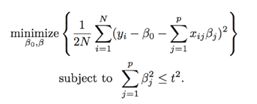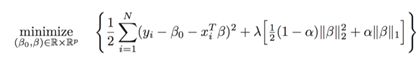Python 房价预测 kaggle 线性回归 SVM 神经网络 随机森林 集成模型
摘要
现如今房产成为大多数家庭总资产中占比最大的一部分,也成为国人投资的重要渠道,研究和预测房产价格对我国人民和宏观经济发展都有重要价值。本文对包含房产各项基本信息及价格的数据进行处理,利用包括线性回归、核岭回归、支持向量回归、神经网络、决策树以及集成方法等多种数据挖掘算法对房产价格构建预测模型,并利用均方误差作为指标对各模型作出了相应评价。总体来看,本文根据房产信息对房产价格做出了较好的预测模型,为房地产相关行业与从业人员提供了较有力的决策依据。
关键词: 房价预测;模型比较;线性模型;集成模型
目录
一、研究背景及意义
1.1 研究背景和研究意义
1.2 研究内容简要介绍
二、数据探索性分析与预处理
2.1数据介绍
2.2数据探索性分析
2.2.1数值型变量
2.2.2 非数值型变量
2.3数据预处理
2.3.1 重复值与异常值处理
2.3.2 缺失值处理
三、数据挖掘建模与分析
3.1数据变换
3.1.1 响应变量
3.1.2 自变量
3.2统一评价与调参方法
3.3线性模型
3.4核方法
3.5神经网络与决策树
3.6集成模型
四、扩展与总结
4.1扩展一:RobustScaler方法
4.2扩展二:变量选择算法尝试
4.3总结
4.4不足与展望
参考文献
附录
1.变量名与中文对照表
2. 全模型lasso的估计系数结果
代码
数据可视化
数据预处理
建模
变量选择算法尝试
注:本文原本是我与其他4人的数据挖掘课程作业,我是矿工头子,负责建模的数据变换到核方法部分,其他四名矿工分别为:LY(可视化)、Maxjiao (缺失值异常值处理)、AY(神经网络决策树集成模型)、TXW(扩展与总结)。
一、研究背景及意义
1.1 研究背景和研究意义
房地产行业在我国国民经济中占支柱地位,对拉动经济增长起到正向影响的同时也对稳定国内经济有重要作用。[1] 现如今房产成为大多数家庭总资产中占比最大的一部分,也成为国人投资的重要渠道,设想若能对房产价格实现准确预测,就相当于通过减少交易双方对房价估计的不确定性为双方都降低了风险与成本。因此,研究和预测房产价格对我国人民和宏观经济发展的重要性不言而喻。
对于购房者来说,如果通过选定房产的地理位置、面积及楼龄等基本信息可以预测出较为准确的房产价格或价格区间,就对其进一步的购房决策提供了参考依据;对于销售方来说,也可以通过相同的方式获取房产的预测价格,避免定价过高而延长房产在市场上的空置时间或是定价过低造成的利润损失;对于房地产开放商来说,也可以将房产信息和价格层次的对应关系作为支撑做出市场定位与经营决策。
1.2 研究内容简要介绍
本文首先将数据集进行可视化,简单直观地刻画出各变量对房价的影响,其次尝试利用线性模型(包括lasso、ridge、elasticnet)、核方法(kernelridge, svr)、神经网络、决策树和集成模型多种方式对房价做出预测,并以均方误差为指标对各模型做出评价和对比分析。
第一章主要介绍对房地产价格预测和研究的背景和意义,以及本文的主要内容与组织结构。
第二章主要对数据进行介绍,做探索性分析、缺失值处理和异常值处理。
第三章分别介绍了几种回归和分类模型,通过对本文选取的房价预测数据的应用,对模型进行比较并将均方误差作为指标来对模型结果做出评价。
最后一章,主要是对本文整体的研究过程进行总结,并对改进方向以及未来研究作出展望。
二、数据探索性分析与预处理
2.1数据介绍
本文选用的房产信息数据取自kaggle数据库,是美国爱荷华州埃姆斯市的房价数据,其中包含三个数据集,分别为测试集、训练集和测试集的标签数据集,训练集含有1460个样本,测试集含有1459个样本。
此数据共包含变量80个,分为79个属性变量和一个响应变量(即房产价格),其中属性变量含36个数值型变量和43个非数值型变量。按照各变量意义将79个属性变量按下表所示分类(各变量中英文对照表参见附录):
表 1 变量分类
| 类别 |
所含变量 |
| 地理位置 |
MSSubClass、MSZoning、LotFrontage、LotArea、Street、Alley、LotShape、LandContour、Utilities、LotConfig、LandSlope、Neighborhood、Condition1、Condition2 |
| 房子风格 |
BldgType、HouseStyle、OverallQual、OverallCond |
| 房子装修 |
YearBuilt、YearRemodAdd、RoofStyle、RoofMatl、Exterior1st、Exterior2nd、MasVnrType、MasVnrArea、ExterQual、ExterCond |
| 地下室 |
Foundation、BsmtQual、BsmtCond、BsmtExposure:、BsmtFinType1、BsmtFinSF1、BsmtFinType2、BsmtFinSF2、BsmtUnfSF、TotalBsmtSF |
| 冷暖气 |
Heating、HeatingQC、CentralAir、Electrical |
| 居住面积 |
1stFlrSF、2ndFlrSF、LowQualFinSF、GrLivArea |
| 功能房间 |
BsmtFullBath、BsmtHalfBath、FullBath、HalfBath、Bedroom、Kitchen、KitchenQual、TotRmsAbvGrd、Functional |
| 车库 |
GarageType、GarageYrBlt、GarageFinish、GarageCars、GarageArea、GarageQual、GarageCond、PavedDrive |
| 其他面积 |
WoodDeckSF、OpenPorchSF、EnclosedPorch、3SsnPorch:、ScreenPorch、PoolArea |
| 销售 |
MoSold、YrSold、SaleType、SaleCondition |
| 其他 |
Fireplaces、FireplaceQu、PoolQC、Fence、MiscFeature、MiscVal |
2.2数据探索性分析
2.2.1数值型变量
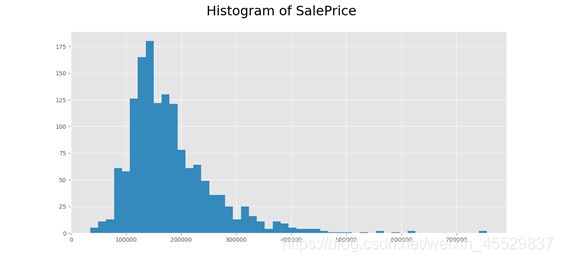
本文的响应变量是房产价格,其分布直方图是一个右偏的偏态分布,这表明大部分房子的房价是比较相近的,均在较合理水平;而少部分房产房价偏高。
图 1 房产价格分布直方图
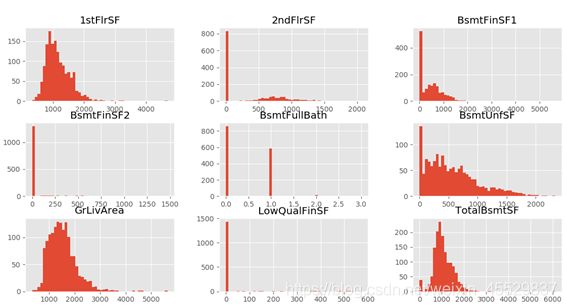
对于数值型的属性变量,首先通过作出其直方图观察其分布,部分可视化结果如下图。通过对变量分布直方图分析可知,数值型变量包含许多离散型的整数变量,用于表明某些特征的个数,如车库容量等。而对于连续型数据来说,一部分变量的直方图与房价的直方图类似,是右偏的偏态分布,如1stFlrSF;同时也有部分变量分布较为极端,数据量仅集中在某个或某几个值,如BsmtFinSF2。
图 2 部分数值型变量分布直方图
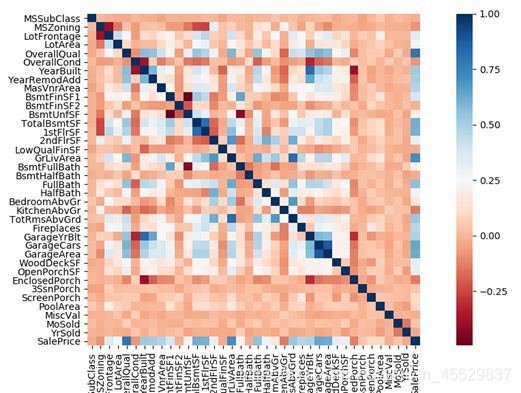
为了探究变量之间的关系,对所有数值型变量作相关性热力图(见图4),发现部分属性变量间高度相关,提示须对高度相关的变量作一定处理,同时也有不少变量都与响应变量间有较强的相关关系。
图 3 数值型变量间相关性热力图
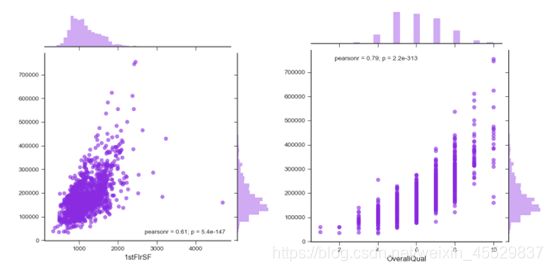
最后,对数值型变量作其对于房价的散点图。观察可知,部分数值型变量的值有比较明显的趋势性,如1stFlrSF 和OverallQual(如图4所示),随变量取值的增大,房价也在攀升,并且成线性趋势。
图 4 部分数值型变量散布图
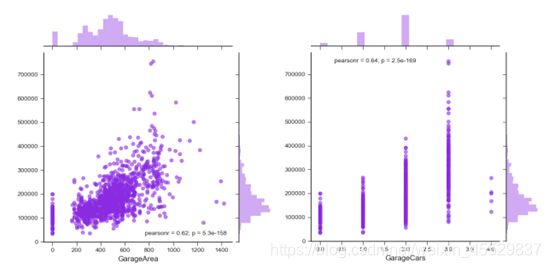
同时,对于同属一个意义类别的变量,由于是对房产同一信息的描述,故而相关性较高,对房价的影响也比较类似。如描述车库的车库面积和车库容量两个变量显然是高度相关的,车库大小基本决定车库容量,故可以选择趋势最为明显的车库面积而去除车库容量来对房价进行描述(两变量分布如图5所示)。
图 5 车库面积与车库容量散布图对比
2.2.2 非数值型变量
对于非数值型的分类变量,作出其关于房价的散点图和盒型图,并将两种图对应观察分析。对于一些变量,大多数数据仅集中在某个普通类别中(例如图6中,变量Condition1数据大多集中于Norm类别),该类别所对应的数据几乎涵盖了所有房价取值,从而无法简单判断该类别对房价的影响;而少量数据分布于特殊类别(例如图6中变量Condition1除Norm以外的其他类别),每一个特殊类别对应房价的分布较为集中,各特殊类别对应房价的分布高低错落。这表明,这些变量在取含样本量较少的类别时对应的房价会有一定倾向,有较强的辨识度,对房价预测可能有重要作用。
图6 部分非数值型变量分布图
有些变量有较多的类别取值,考虑根据房价在每一个类别取值的变化程度来分析,变化越大,表明该变量对房价的影响越大。进一步,为了方便观察,对它们按均值进行了排序。比如变量neighborhood,排序后发现,房价跨度从1万到3万,随该变量取值的变化有较明显的变化趋势(如图7),说明该变量与房价关系较密切。
图 7 变量 Neighborhood 分布图
但也有少数变量在几个类别下样本的数量及分布情况没有显著差别,表示该变量与房价的关系可能较弱。
综合来看,对数据的探索性分析一方面直观展示了各变量的分布情况,也对变量选择提供了一定的依据与支撑。
2.3数据预处理
首先将三个原始数据集进行整合,先将测试集与对应的标签集按照id横向合并,再将训练集与得到的完整测试集纵向合并,在以此得到的新数据集上进行数据处理的相关操作。
2.3.1 重复值与异常值处理
对数据作重复值检测,发现无重复值,故无需处理。
通过对变量作箱线图,发现部分变量异常值较多,但考虑到变量异常值对房价预测有重要价值,故不对异常值做处理。
2.3.2 缺失值处理
首先对数据集按行检测缺失值,发现每行都含有缺失值,缺失率达100%。
再对变量检测缺失值,发现共有35个变量包含有缺失值,其中缺失率最高的有关于游泳池的变量,缺失率高达百分之九十九点六,这也就可以解释了数据行缺失率100%了。
对有较高缺失率的变量,虽然缺失较多,但是在数据预处理阶段,为了保证尽量多的信息被保留下来,所以在预处理阶段不首先考虑数据变量删除。这里结合数据集变量间有相关关系,考虑按照表1的变量分类,利用变量之间的相关性进行缺失值处理。具体操作列举如下:
- 对于游泳池类型变量,利用PoolQC(包含有缺失值)与另一个相关变量PoolArea(不包含有缺失值),筛选出PoolArea有值但PoolQC缺失的数据行,并计算出PoolQC各标签对应的PoolArea的平均面积,通过比较距离,对筛选出的数据行PoolQC变量进行填充,剩余PoolQC为Na的值替换为none值;
- 对于车库类数据:类似于游泳池数据,查找相互之间不匹配数据,作为待处理项目,利用众数填补办法对部分缺失值进行处理。但是在车库数据中包含有一项GarageTrBlt数据,是车库的建成年限是数值类数据,但此处用0替换,显然不合理,所以用建成年限里最小值进行替换即1895替换;
- 对于单板类变量:单板数据同样采用空值和0值进行替换,但是在单板数据中存在有异常值,即存在有部分MasVnrType类型为None,但是Area!=0的数据,这个就需要调用之前得到的原始数据变量标签统计,发现在原数据中就存在有空值,这就导致了MasVnrType类型为None,但是Area!=0数据的存在,但是由于三个标签的均值相差不大,不能很好地区分,所以此处选择删去这类异常值;
- 对于街道线数据:考虑街道线填充空值不合适,所以通过街道线和Neighborhood(房屋附近位置)的相关关系进行填充,此处利用groupby函数进行填充。
对于缺失率低于0.07%的变量,经计算发现其缺失值小于等于2,所以对于这类变量考虑使用简单的插补法,或者数据删除进行处理。
最后将经过预处理的数据按照原始数据的训练集和测试集比例重新拆分得到处理过后的训练集和测试集。
三、数据挖掘建模与分析
3.1数据变换
3.1.1 响应变量
通过对数值型变量SalePrice绘制直方图、密度图和计算偏度峰度发现,响应变量分布呈现右偏、高峰度及偏离正态的特点;再对训练数据做K-S检验,Kolmogorov–Smirnov 检验基于累积分布函数,用于检验一个经验分布是否符合某种理论分布,检验结果D = 0.12369, p-value < 2.2e-16,则不拒绝原假设,样本点不符合正态分布。
故对其做对数平滑变换,从而减少其峰度和偏度,使其更符合回归模型数据的正态性假定;再对变换后的数据进行K-S检验,检验结果D = 0.52055, p-value = 0.9494,则不拒绝原假设,认为变换后的数据符合正态理论分布,适合进一步的回归建模。
3.1.2 自变量
对于连续型自变量,对峰度较高的变量作box-cox变换,box-cox变换是一种常用的数据变换方法,这里用于让分布在不丢失信息的前提下,具有更好的性质(独立性、方差齐性、正态性等)[3],以便得到更好的模型。
对于分类型自变量,将其转换为哑变量,进一步提高模型精度,检验不同变量类别对响应变量的影响。
3.2统一评价与调参方法
本文采用交叉验证均方根误差作为模型评价指标。均方根误差(RMSE)是预测值与真实值偏差的平方与观测次数n比值的平方根,即:
能够很好地衡量预测值同真值之间的偏差。进一步通过k重交叉验证,提高所得指标的精度和稳定性,本文中采用5折交叉验证方法。
采用循环搜索以及python-sklearn里常用的网格搜索(GridSearchCV)和随机搜索(RandomizedSearchCV)方法对模型进行调参。
3.3线性模型
在线性模型部分本文选取了OLS线性回归、Lasso、Ridge及Elastic Net四种模型对本文数据集进行应用。其中OLS线性回归通过最小化误差的平方和寻找数据的最佳函数匹配,模型原理较简单,这里主要对后三种模型原理做简要介绍。
Lasso方法在普通线性模型中增加L1惩罚项,对于普通线性模型Lasso估计为
其中λ为调节系数,对调节系数的适当选择可以将不显著的变量系数压缩至零,产生稀疏结果,从而降低自变量的维度,达到减小模型复杂度的作用[4]。
而Ridge方法是L2正则化,在普通线性模型中的估计为
其中t为调节系数。可以发现Ridge估计是有偏的,是对最小二乘估计以同一比例的压缩结果,没有稀疏性,且任一系数都不会被压缩至零,保留了模型的全部变量。
在Lasso方法回归太过(太多特征被稀疏为0),而Ridge方法也正则化不够(回归系数衰减太慢)的时候,使用ElasticNet回归来综合L1正则化项和L2正则化项可以得到比较好的结果,其估计公式为:
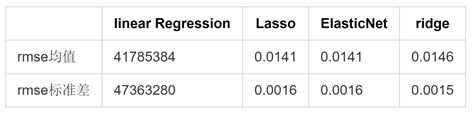
将以上四种模型应用于本文所选数据集,得到评价指标对比结果如下表所示,可以看出普通线性回归的结果由于对噪音十分敏感得到的结果稳定性极低,而正则化能够极大地提升线性模型的预测准确度。
表 2 线性模型结果对比
3.4核方法
核方法 是一类把低维空间的非线性可分问题,转化为高维空间的线性可分问题的方法,可以用于数据为非线性可分的算法。这一部分我们选用了核岭回归(KRR) 与支持向量回归(SVR)两种模型。
KRR和SVR都通过采用核技巧来学习非线性函数,它们的损失函数不同。一般来说,对于中型训练集(小于1000个样本),拟合KRR比SVR快; 然而,对于更大的训练集,SVR可以更好地扩展。关于预测时间,由于学习的稀疏解,所以SVR快于KRR。但需要注意稀疏程度以及预测时间取决于SVR的参数。
两种模型的应用结果对比如下表,可以看到支持向量回归模型总体上结果不如核岭回归模型,但两线性核模型表现都不错。
表 3 KRR与SVR评价指标(RMSE)对比
3.5神经网络与决策树
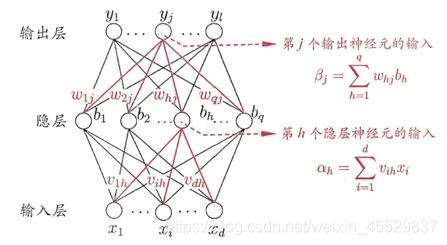
神经网络是一种模仿生物神经网络的结构和功能的数学模型或计算模型,由大量的节点(或称“神经元”)和之间相互的联接构成,每个节点代表一种特定的输出函数,称为激活函数(activation function),每两个节点间的联接都代表一个对于通过该连接信号的加权值,称之为权重。网络的输出依网络的连接方式、权重值和激励函数的不同而不同。
表 4 神经网络原理图示
决策树算法通常是一个递归地选择最优特征,并根据该特征对训练数据进行分割,使得各个子数据集有一个最好的分类的过程。具体构造方法简述为:构建根节点,选择一个最优特征,对训练数据集进行分割,使得各个子集有一个在当前条件下最好的分类,构建出相应的节点,递归进行,直至所有训练数据子集被基本正确的分类,或者没有合适的特征为止,这样就生成了一颗决策树。
分类树叶节点是一个类别,而回归树叶节点是一个个具体的值。当特征数据是连续值时,就需要先对数据进行离散化处理。(如考试得分0~100,1~59为不及格,60~80为达标,80~100为优秀)这样离散处理后的数据就可以用来构建决策树了。
应用两模型得到结果对比如下表所示。
表 5 神经网络与决策树结果对比
| 指标 |
神经网络 |
决策树 |
| RMSE均值 |
0.0171 |
0.0222 |
| RMSE标准差 |
0.0013 |
0.0013 |
3.6集成模型
集成学习是一种机器学习范式,训练多个模型解决相同的问题,并将它们结合起来以获得更好的结果。当多个模型被正确组合时,可以得到更精确的模型。本文中选用了bagging和stacking两种集成方法。bagging 的目标在于生成比单个模型稳定性更好的集成模型,而stacking 通常考虑的是异质弱学习器(不同的学习算法被组合在一起),并通过训练一个元模型来组合它们,然后基于这些弱模型返回的多个预测结果输出最终的预测结果。
两种集成方法得到的结果分别为:
表 6 bagging集成模型结果
| 指标 |
SVR |
随机森林 |
ElasticNet |
| RMSE均值 |
0.0357 |
0.0174 |
0.0142 |
| RMSE标准差 |
0.0025 |
0.0005 |
0.0017 |
表 7 stacking 集成模型结果
| 指标 |
Ridge |
随机森林 |
MLPRegressor |
| RMSE均值 |
0.0185 |
0.0182 |
0.0160 |
| RMSE标准差 |
0.0014 |
0.0014 |
0.0014 |
四、扩展与总结
4.1扩展一:RobustScaler方法
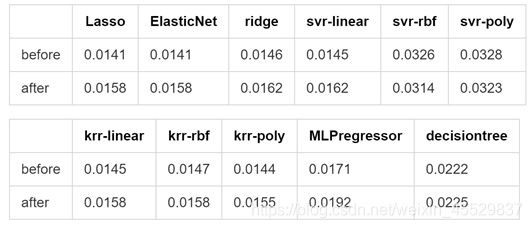
由于本文采用的数据集异常值较多且有重要价值,考虑到异常点容易在数据标准化后失去其离群特征,故在数据标准化时考虑采用RobustScaler方法做处理,此方法根据分位数范围(默认为IQR:Interquartile Range)删除中位数并缩放数据,鲁棒性很好。增加RobustScaler处理后,再次将数据带入上文模型,rmse前后对比如下。
表 8 RobustScaler扩展结果
从上表可以看出,ridge,svr-rbf,svr-poly,krr-rbf,krr-poly,MLPregressor和decisiontree的rmse具有轻微改进,总体而言,增加RobustScaler算法后效果较好。
4.2扩展二:变量选择算法尝试
首先,根据探索性分析得到的结果,选出分布图趋势较为明显或辨识度较高的变量,再结合实际情况,选出与购房者在购买房产时可能会主要考虑的各方面需求相关的变量,对重要变量作初步汇总。
由于含有高度相关的变量,考虑到传统lasso方法在处理高度相关变量时有一定局限性,因此采取通过生成数据的bootstrap样本并对每个样本做基本特征选择算法的方式做稳定性选择。[2]
最终选择出的变量汇总如下表:
表 9 变量选择结果
| 变量名 |
中文对照 |
类别 |
| MSSubClass |
建筑类 |
地理位置 |
| MSZoning |
城市总体规划分区 |
地理位置 |
| Alley |
巷类型 |
地理位置 |
| Neighborhood |
城市范围内的物理位置 |
地理位置 |
| Condition1 |
接近主干道或铁路 |
地理位置 |
| Condition2 |
接近主路或铁路 |
地理位置 |
| BldgType |
住宅类型 |
风格 |
| OverallQual |
整体质量和表面质量 |
风格 |
| RoofStyle |
屋顶类型 |
装修 |
| RoofMatl |
屋顶材料 |
装修 |
| Exterior1st |
房屋外墙 |
装修 |
| 1stFlrSF |
一楼面积 |
居住面积 |
| GrLivArea |
高档(地面)居住面积 |
居住面积 |
| Street |
道路入口类型 |
地理位置 |
| LotConfig |
地产配置 |
地理位置 |
| HouseStyle |
居家风格 |
风格 |
| OverallCond |
总体状态额定值 |
风格 |
| YearBuilt |
原施工日期 |
装修 |
| BsmtQual |
地下室的高度 |
地下室 |
| CentralAir |
空调 |
冷暖气 |
| Electrical |
电气系统 |
冷暖气 |
| BedroomAbvGr |
地下室层以上的卧室数 |
功能房间 |
| TotRmsAbvGrd |
总房间(不包括浴室) |
功能房间 |
| GarageArea |
车库大小 |
车库 |
| SaleCondition |
销售条件 |
销售 |
把上表的变量带入上文的模型中,得到前后rmse对比见表10,发现只有svr-rbf,svr-poly的rmse有所下降,大部分方法的rmse都有所上升,猜测是由于变量选少了而丧失了一部分重要信息。
表10 变量选择算法尝试结果
4.3总结
1.在所有应用的模型中,全模型的Lasso回归效果最好,该模型的alpha值为7.8372e-05,在测试集上的rmse为0.043,该模型的估计系数见附录。
2.结合实际将对房产价格有重要影响的因素分为以下几类:地理位置(所处城市规划分区、是否接近主干道等)、装修风格与质量(外墙、屋顶材料与风格等)、居住面积、房间数和附加价值(空调、车库、地下室等),该结论与常识较为符合。
4.4不足与展望
经分析讨论,认为本文有以下不足,今后的研究可从以下方面考虑进行改善。
本文仅选取均方误差作为模型的评价指标,虽然会使模型间的对比分析更加容易,但毕竟较为单一,会降低一定的全面性与可信度;变量选择方法由于与数据可视化结果进行了结合,故包含有一定的主观成分,且由于对扩展算法研究不够深入和细致,模型尝试结果并不是很好。
参考文献
- 肖卫国,陈宇,尹智超.房地产价格对中国宏观经济的影响研究[J].统计与决策,2016(02):124-126.
- Meinshausen, N. and Buhlmann, P., 2010. Stability selection. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 72(4), pp.417-473.
- 荆庆林.线性回归及其应用研究.吉林大学出版社,2012.12
- Tibshirani, R. (1996). Regression shrinkage and selection via the lasso. J. Royal. Statist. Soc B., Vol. 58, No. 1, pages 267-288).
附录
1.变量名与中文对照表
| 变量名 |
中文对照 |
| MSSubClass |
建筑类 |
| MSZoning |
城市总体规划分区 |
| LotFrontage |
连接物业的街道线 |
| LotArea |
方块大小 |
| Street |
道路入口类型 |
| Alley |
巷类型 |
| LotShape |
地产的外形 |
| LandContour |
地产的扁平化 |
| Utilities |
地产的公用事业类型 |
| LotConfig |
地产配置 |
| LandSlope |
地产的坡 |
| Neighborhood |
城市范围内的物理位置 |
| Condition1 |
接近主干道或铁路 |
| Condition2 |
接近主路或铁路 |
| BldgType |
住宅类型 |
| HouseStyle |
居家风格 |
| OverallQual |
整体质量和表面质量 |
| OverallCond |
总体状态额定值 |
| YearBuilt |
原施工日期 |
| YearRemodAdd |
重塑日期 |
| RoofStyle |
屋顶类型 |
| RoofMatl |
屋顶材料 |
| Exterior1st |
房屋外墙 |
| Exterior2nd |
外部第二层:房屋外部覆盖物 |
| MasVnrType |
圬工单板型 |
| MasVnrArea |
砌体单板覆盖面积 |
| ExterQual |
外观材质 |
| ExterCond |
外墙材料的现状 |
| Foundation |
地基类型 |
| BsmtQual |
地下室的高度 |
| BsmtCond |
地下室概况 |
| BsmtExposure |
走道或花园式地下室墙 |
| BsmtFinType1 |
地下室竣工面积质量 |
| BsmtFinSF1 |
1型成品面积 |
| BsmtFinType2 |
第二成品区域的质量(如果存在) |
| BsmtFinSF2 |
2型成品面积 |
| BsmtUnfSF |
地下室面积 |
| TotalBsmtSF |
地下室面积总计面积 |
| Heating |
暖气方式 |
| HeatingQC |
暖气质量与条件 |
| CentralAir |
空调 |
| Electrical |
电气系统 |
| 1stFlrSF |
一楼面积 |
| 2ndFlrSF |
二楼面积 |
| LowQualFinSF |
低质量完工面积(所有楼层) |
| GrLivArea |
高档(地面)居住面积 |
| BsmtFullBath |
地下室全浴室 |
| BsmtHalfBath |
地下室半浴室 |
| FullBath |
高档浴室 |
| HalfBath |
半日以上洗澡浴室 |
| BedroomAbvGr |
地下室层以上的卧室数 |
| KitchenAbvGr |
厨房数量 |
| KitchenQual |
厨房品质 |
| TotRmsAbvGrd |
总房间(不包括浴室) |
| Functional |
家庭功能评级 |
| Fireplaces |
壁炉数 |
| FireplaceQu |
壁炉质量 |
| GarageType |
车库位置 |
| GarageYrBlt |
车库建成年 |
| GarageFinish |
车库的内饰 |
| GarageCars |
车库容量大小 |
| GarageArea |
车库大小 |
| GarageQual |
车库质量 |
| GarageCond |
车库状况 |
| PavedDrive |
铺好的车道 |
| WoodDeckSF |
木制甲板面积 |
| OpenPorchSF |
外部走廊面积 |
| EnclosedPorch |
闭走廊面积 |
| 3SsnPorch |
三季走廊面积 |
| ScreenPorch |
屏风走廊面积 |
| PoolArea |
泳池面积 |
| PoolQC |
泳池的质量 |
| Fence |
围栏质量 |
| MiscFeature |
其他类别的杂项特征 |
| MiscVal |
杂项价值 |
| MoSold |
月售出 |
| YrSold |
年销售 |
| SaleType |
销售类型 |
| SaleCondition |
销售条件 |
| SalePrice |
以美元出售的房产价格 |
2. 全模型lasso的估计系数结果
代码
数据可视化
import os
os.chdir('E:/2 moon/大三下/数据挖掘/期末作业安排/房价预测')
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns
train=pd.read_csv("train.csv")
Y_test=pd.read_csv("sample_submission.csv")
train.head() #有连续型数据,有离散型类别数据
train.shape #1460个样本,81列(80个变量,第一个变量是id,最后一个是响应变量房价)
train.iloc[:,0:41].dtypes #整数数据,浮点型数据,object类别型数据
train.iloc[:,41:82].dtypes #将结果整理为excle表variable_type方便后续查阅
train.info
train['MSSubClass'].value_counts()
train['MSZoning'].value_counts()
train['OverallQual'].value_counts()
plt.style.use('ggplot')
# =================数值型变量================================
# 直方图
train.iloc[:,1:16].hist(bins=50,figsize=(16,9))
train.iloc[:,16:32].hist(bins=50,figsize=(16,9))
train.iloc[:,32:48].hist(bins=50,figsize=(16,9))
train.iloc[:,48:60].hist(bins=50,figsize=(16,9))
train.iloc[:,60:70].hist(bins=50,figsize=(16,9))
train.iloc[:,70:81].hist(bins=50,figsize=(16,9))
# 盒图部分
data1=train.iloc[:,[3, 26, 59]]
data2=train.iloc[:,[1, 4, 17, 18, 19, 20, 34, 36, 37, 38, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 54, 56, 61, 62, 66, 67, 68, 69, 70, 71, 75, 76, 77, 80]]
data_1=data1.values
data_2=data2.values
plt.boxplot(data_2[:,2:29])#, notch=False, vert=True)
# 相关系数图(热力图)
#df=train.iloc[:,[1,2,3,4,17,18,19,20,26,34,36,37,38,43,44,45,46,47,48,49,50,51,52,54,56,59,61,62,66,67,68,69,70,71,75,76,77,80]]
#dfdata = df.corr()
ylabels=df.columns
dfdata2=train.corr()
plt.subplots(figsize=(20, 15))
sns.heatmap(dfdata2, annot=False, vmax=1, square=True,yticklabels=ylabels,xticklabels=ylabels, cmap="RdBu")
# 与房价的散点图
sns.set_style('ticks')
sns.jointplot(x='MSSubClass', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='LotFrontage', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='LotArea', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='OverallQual', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='OverallCond', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='YearBuilt', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='YearRemodAdd', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='MasVnrArea', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='BsmtFinSF1', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='BsmtFinSF2', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='BsmtUnfSF', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='TotalBsmtSF', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='1stFlrSF', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='2ndFlrSF', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='LowQualFinSF', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='GrLivArea', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='BsmtFullBath', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='BsmtHalfBath', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='FullBath', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='HalfBath', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='BedroomAbvGr', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='KitchenAbvGr', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='TotRmsAbvGrd', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='Fireplaces', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='GarageYrBlt', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='GarageCars', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='GarageArea', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6) #有断崖
sns.jointplot(x='WoodDeckSF', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='OpenPorchSF', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='EnclosedPorch', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='3SsnPorch', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='ScreenPorch', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='PoolArea', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='MiscVal', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='MoSold', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
sns.jointplot(x='YrSold', y='SalePrice', data = train, color = 'blueviolet', alpha=0.6)
# =====================分类型变量==========================
#df=train.select_dtypes(exclude=['object'])
train['MSZoning'].value_counts()
train['Street'].value_counts()
train['Alley'].value_counts()
train['LotShape'].value_counts()
train['LandContour'].value_counts()
train['Utilities'].value_counts()
train['LotConfig'].value_counts()
train['LandSlope'].value_counts()
train['Neighborhood'].value_counts()
train['Condition1'].value_counts()
train['Condition2'].value_counts()
train['BldgType'].value_counts()
train['HouseStyle'].value_counts()
train['RoofStyle'].value_counts()
train['RoofMatl'].value_counts()
train['Exterior1st'].value_counts()
train['Exterior2nd'].value_counts()
train['MasVnrType'].value_counts()
train['ExterQual'].value_counts()
train['ExterCond'].value_counts()
train['Foundation'].value_counts()
train['BsmtQual'].value_counts()
train['BsmtCond'].value_counts()
train['BsmtExposure'].value_counts()
train['BsmtFinType1'].value_counts()
train['BsmtFinType2'].value_counts()
train['Heating'].value_counts()
train['HeatingQC'].value_counts()
train['CentralAir'].value_counts()
train['Electrical'].value_counts()
train['KitchenQual'].value_counts()
train['Functional'].value_counts()
train['FireplaceQu'].value_counts()
train['GarageType'].value_counts()
train['KitchenQual'].value_counts()
train['GarageFinish'].value_counts()
train['GarageQual'].value_counts()
train['GarageCond'].value_counts()
train['PavedDrive'].value_counts()
train['PoolQC'].value_counts()
train['Fence'].value_counts()
train['MiscFeature'].value_counts()
train['SaleType'].value_counts()
train['SaleCondition'].value_counts()
# swarmplot用特定算法使得三点避免覆盖,运行速度较慢
#f1=plt.figure()
#f1.add_subplot(2,2,1)
#sns.swarmplot(x="MSSubClass", y="SalePrice", data=train)
#f1.add_subplot(2,2,3)
#sns.boxplot(x="MSSubClass", y="SalePrice", data=train)
#f1.add_subplot(2,2,2)
#sns.swarmplot(x="MSZoning", y="SalePrice", data=train)
#f1.add_subplot(2,2,4)
#sns.boxplot(x="MSZoning", y="SalePrice", data=train)
# 用抖动的方法使得散点避免覆盖,运行速度快一点
f1=plt.figure()
f1.add_subplot(2,2,1)
sns.stripplot(x="MSZoning", y="SalePrice", data=train, alpha=0.6,jitter=True)
f1.add_subplot(2,2,3)
sns.boxplot(x="MSZoning", y="SalePrice", data=train)
f1.add_subplot(2,2,2)
sns.stripplot(x="Street", y="SalePrice", data=train, alpha=0.6,jitter=True)
f1.add_subplot(2,2,4)
sns.boxplot(x="Street", y="SalePrice", data=train)
plt.suptitle('Graphs of Non-numeric variables', size=23)
f2=plt.figure()
f2.add_subplot(2,2,1)
sns.stripplot(x="Alley", y="SalePrice", data=train, alpha=0.6,jitter=True)
f2.add_subplot(2,2,3)
sns.boxplot(x="Alley", y="SalePrice", data=train)
f2.add_subplot(2,2,2)
sns.stripplot(x="LotShape", y="SalePrice", data=train, alpha=0.6,jitter=True)
f2.add_subplot(2,2,4)
sns.boxplot(x="LotShape", y="SalePrice", data=train)
plt.suptitle('Graphs of Non-numeric variables', size=23)
f3=plt.figure()
f3.add_subplot(2,2,1)
sns.stripplot(x="LandContour", y="SalePrice", data=train, alpha=0.6,jitter=True)
f3.add_subplot(2,2,3)
sns.boxplot(x="LandContour", y="SalePrice", data=train)
f3.add_subplot(2,2,2)
sns.stripplot(x="Utilities", y="SalePrice", data=train, alpha=0.6,jitter=True)
f3.add_subplot(2,2,4)
sns.boxplot(x="Utilities", y="SalePrice", data=train)
plt.suptitle('Graphs of Non-numeric variables', size=23)
f4=plt.figure()
f4.add_subplot(2,2,1)
sns.stripplot(x="LotConfig", y="SalePrice", data=train, alpha=0.6,jitter=True)
f4.add_subplot(2,2,3)
sns.boxplot(x="LotConfig", y="SalePrice", data=train)
f4.add_subplot(2,2,2)
sns.stripplot(x="LandSlope", y="SalePrice", data=train, alpha=0.6,jitter=True)
f4.add_subplot(2,2,4)
sns.boxplot(x="LandSlope", y="SalePrice", data=train)
plt.suptitle('Graphs of Non-numeric variables', size=23)
group_region = train.groupby('Neighborhood')
avg_price = group_region.aggregate({'SalePrice':np.mean}).sort_values('SalePrice', ascending = False)
f5=plt.figure()
f5.add_subplot(2,1,1)
sns.stripplot(x="Neighborhood", y="SalePrice", data=train, alpha=0.6,jitter=True, order = avg_price.index)
plt.tick_params(labelsize=6) #设置横坐标字体大小
f5.add_subplot(2,1,2)
sns.boxplot(x="Neighborhood", y="SalePrice", data=train, order = avg_price.index)
plt.tick_params(labelsize=6)
plt.suptitle('Graphs of Non-numeric variables', size=23)
group_region6 = train.groupby('Condition1')
avg_price6 = group_region6.aggregate({'SalePrice':np.mean}).sort_values('SalePrice', ascending = False)
group_region6_2 = train.groupby('Condition2')
avg_price6_2 = group_region6_2.aggregate({'SalePrice':np.mean}).sort_values('SalePrice', ascending = False)
f6=plt.figure()
f6.add_subplot(2,2,1)
sns.stripplot(x="Condition1", y="SalePrice", data=train, alpha=0.6,jitter=True, order = avg_price6.index)
f6.add_subplot(2,2,3)
sns.boxplot(x="Condition1", y="SalePrice", data=train, order = avg_price6.index)
f6.add_subplot(2,2,2)
sns.stripplot(x="Condition2", y="SalePrice", data=train, alpha=0.6,jitter=True, order = avg_price6_2.index)
f6.add_subplot(2,2,4)
sns.boxplot(x="Condition2", y="SalePrice", data=train, order = avg_price6_2.index)
plt.suptitle('Graphs of Non-numeric variables', size=23)
group_region7 = train.groupby('BldgType')
avg_price7 = group_region7.aggregate({'SalePrice':np.mean}).sort_values('SalePrice', ascending = False)
group_region7_2 = train.groupby('HouseStyle')
avg_price7_2 = group_region7_2.aggregate({'SalePrice':np.mean}).sort_values('SalePrice', ascending = False)
f7=plt.figure()
f7.add_subplot(2,2,1)
sns.stripplot(x="BldgType", y="SalePrice", data=train, alpha=0.6,jitter=True, order = avg_price7.index)
f7.add_subplot(2,2,3)
sns.boxplot(x="BldgType", y="SalePrice", data=train, order = avg_price7.index)
f7.add_subplot(2,2,2)
sns.stripplot(x="HouseStyle", y="SalePrice", data=train, alpha=0.6,jitter=True, order = avg_price7_2.index)
f7.add_subplot(2,2,4)
sns.boxplot(x="HouseStyle", y="SalePrice", data=train, order = avg_price7_2.index)
plt.suptitle('Graphs of Non-numeric variables', size=23)
group_region8 = train.groupby('RoofStyle')
avg_price8 = group_region8.aggregate({'SalePrice':np.mean}).sort_values('SalePrice', ascending = False)
group_region8_2 = train.groupby('RoofMatl')
avg_price8_2 = group_region8_2.aggregate({'SalePrice':np.mean}).sort_values('SalePrice', ascending = False)
f8=plt.figure()
f8.add_subplot(2,2,1)
sns.stripplot(x="RoofStyle", y="SalePrice", data=train, alpha=0.6,jitter=True, order = avg_price8.index)
f8.add_subplot(2,2,3)
sns.boxplot(x="RoofStyle", y="SalePrice", data=train, order = avg_price8.index)
f8.add_subplot(2,2,2)
sns.stripplot(x="RoofMatl", y="SalePrice", data=train, alpha=0.6,jitter=True, order = avg_price8_2.index)
plt.tick_params(labelsize=8)
f8.add_subplot(2,2,4)
sns.boxplot(x="RoofMatl", y="SalePrice", data=train, order = avg_price8_2.index)
plt.tick_params(labelsize=8)
plt.suptitle('Graphs of Non-numeric variables', size=23)
#import gc (garbage collector) 释放一点内存
#del f1, f2, f3, f4, f5, f6, f7, f8
#gc.collect()
group_region9 = train.groupby('Exterior1st')
avg_price9 = group_region9.aggregate({'SalePrice':np.mean}).sort_values('SalePrice', ascending = False)
group_region9_2 = train.groupby('Exterior2nd')
avg_price9_2 = group_region9_2.aggregate({'SalePrice':np.mean}).sort_values('SalePrice', ascending = False)
f9=plt.figure()
f9.add_subplot(2,2,1)
sns.stripplot(x="Exterior1st", y="SalePrice", data=train, alpha=0.6,jitter=True, order = avg_price9.index)
plt.tick_params(labelsize=5)
f9.add_subplot(2,2,3)
sns.boxplot(x="Exterior1st", y="SalePrice", data=train, order = avg_price9.index)
plt.tick_params(labelsize=5)
f9.add_subplot(2,2,2)
sns.stripplot(x="Exterior2nd", y="SalePrice", data=train, alpha=0.6,jitter=True, order = avg_price9_2.index)
plt.tick_params(labelsize=5)
f9.add_subplot(2,2,4)
sns.boxplot(x="Exterior2nd", y="SalePrice", data=train, order = avg_price9_2.index)
plt.tick_params(labelsize=5)
plt.suptitle('Graphs of Non-numeric variables', size=23)
f10=plt.figure()
f10.add_subplot(2,2,1)
sns.stripplot(x="MasVnrType", y="SalePrice", data=train, alpha=0.6,jitter=True)
f10.add_subplot(2,2,3)
sns.boxplot(x="MasVnrType", y="SalePrice", data=train)
f10.add_subplot(2,2,2)
sns.stripplot(x="ExterQual", y="SalePrice", data=train, alpha=0.6,jitter=True)
f10.add_subplot(2,2,4)
sns.boxplot(x="ExterQual", y="SalePrice", data=train)
plt.suptitle('Graphs of Non-numeric variables', size=23)
f11=plt.figure()
f11.add_subplot(2,2,1)
sns.stripplot(x="ExterCond", y="SalePrice", data=train, alpha=0.6,jitter=True)
f11.add_subplot(2,2,3)
sns.boxplot(x="ExterCond", y="SalePrice", data=train)
f11.add_subplot(2,2,2)
sns.stripplot(x="Foundation", y="SalePrice", data=train, alpha=0.6,jitter=True)
f11.add_subplot(2,2,4)
sns.boxplot(x="Foundation", y="SalePrice", data=train)
plt.suptitle('Graphs of Non-numeric variables', size=23)
f12=plt.figure()
f12.add_subplot(2,2,1)
sns.stripplot(x="BsmtQual", y="SalePrice", data=train, alpha=0.6,jitter=True)
f12.add_subplot(2,2,3)
sns.boxplot(x="BsmtQual", y="SalePrice", data=train)
f12.add_subplot(2,2,2)
sns.stripplot(x="BsmtCond", y="SalePrice", data=train, alpha=0.6,jitter=True)
f12.add_subplot(2,2,4)
sns.boxplot(x="BsmtCond", y="SalePrice", data=train)
plt.suptitle('Graphs of Non-numeric variables', size=23)
f13=plt.figure()
f13.add_subplot(2,2,1)
sns.stripplot(x="BsmtExposure", y="SalePrice", data=train, alpha=0.6,jitter=True)
f13.add_subplot(2,2,3)
sns.boxplot(x="BsmtExposure", y="SalePrice", data=train)
f13.add_subplot(2,2,2)
sns.stripplot(x="BsmtFinType1", y="SalePrice", data=train, alpha=0.6,jitter=True)
f13.add_subplot(2,2,4)
sns.boxplot(x="BsmtFinType1", y="SalePrice", data=train)
plt.suptitle('Graphs of Non-numeric variables', size=23)
group_region14 = train.groupby('BsmtFinType2')
avg_price14 = group_region14.aggregate({'SalePrice':np.mean}).sort_values('SalePrice', ascending = False)
group_region14_2 = train.groupby('Heating')
avg_price14_2 = group_region14_2.aggregate({'SalePrice':np.mean}).sort_values('SalePrice', ascending = False)
f14=plt.figure()
f14.add_subplot(2,2,1)
sns.stripplot(x="BsmtFinType2", y="SalePrice", data=train, alpha=0.6,jitter=True, order = avg_price14.index)
f14.add_subplot(2,2,3)
sns.boxplot(x="BsmtFinType2", y="SalePrice", data=train, order = avg_price14.index)
f14.add_subplot(2,2,2)
sns.stripplot(x="Heating", y="SalePrice", data=train, alpha=0.6,jitter=True, order = avg_price14_2.index)
f14.add_subplot(2,2,4)
sns.boxplot(x="Heating", y="SalePrice", data=train, order = avg_price14_2.index)
plt.suptitle('Graphs of Non-numeric variables', size=23)
f15=plt.figure()
f15.add_subplot(2,2,1)
sns.stripplot(x="HeatingQC", y="SalePrice", data=train, alpha=0.6,jitter=True)
f15.add_subplot(2,2,3)
sns.boxplot(x="HeatingQC", y="SalePrice", data=train)
f15.add_subplot(2,2,2)
sns.stripplot(x="CentralAir", y="SalePrice", data=train, alpha=0.6,jitter=True)
f15.add_subplot(2,2,4)
sns.boxplot(x="CentralAir", y="SalePrice", data=train)
plt.suptitle('Graphs of Non-numeric variables', size=23)
f16=plt.figure()
f16.add_subplot(2,2,1)
sns.stripplot(x="Electrical", y="SalePrice", data=train, alpha=0.6,jitter=True)
f16.add_subplot(2,2,3)
sns.boxplot(x="Electrical", y="SalePrice", data=train)
f16.add_subplot(2,2,2)
sns.stripplot(x="KitchenQual", y="SalePrice", data=train, alpha=0.6,jitter=True)
f16.add_subplot(2,2,4)
sns.boxplot(x="KitchenQual", y="SalePrice", data=train)
plt.suptitle('Graphs of Non-numeric variables', size=23)
group_region17 = train.groupby('Functional')
avg_price17 = group_region17.aggregate({'SalePrice':np.mean}).sort_values('SalePrice', ascending = False)
group_region17_2 = train.groupby('FireplaceQu')
avg_price17_2 = group_region17_2.aggregate({'SalePrice':np.mean}).sort_values('SalePrice', ascending = False)
f17=plt.figure()
f17.add_subplot(2,2,1)
sns.stripplot(x="Functional", y="SalePrice", data=train, alpha=0.6,jitter=True, order = avg_price17.index)
f17.add_subplot(2,2,3)
sns.boxplot(x="Functional", y="SalePrice", data=train, order = avg_price17.index)
f17.add_subplot(2,2,2)
sns.stripplot(x="FireplaceQu", y="SalePrice", data=train, alpha=0.6,jitter=True, order = avg_price17_2.index)
f17.add_subplot(2,2,4)
sns.boxplot(x="FireplaceQu", y="SalePrice", data=train, order = avg_price17_2.index)
plt.suptitle('Graphs of Non-numeric variables', size=23)
group_region18 = train.groupby('GarageType')
avg_price18 = group_region18.aggregate({'SalePrice':np.mean}).sort_values('SalePrice', ascending = False)
group_region18_2 = train.groupby('GarageFinish')
avg_price18_2 = group_region18_2.aggregate({'SalePrice':np.mean}).sort_values('SalePrice', ascending = False)
f18=plt.figure()
f18.add_subplot(2,2,1)
sns.stripplot(x="GarageType", y="SalePrice", data=train, alpha=0.6,jitter=True, order = avg_price18.index)
f18.add_subplot(2,2,3)
sns.boxplot(x="GarageType", y="SalePrice", data=train, order = avg_price18.index)
f18.add_subplot(2,2,2)
sns.stripplot(x="GarageFinish", y="SalePrice", data=train, alpha=0.6,jitter=True, order = avg_price18_2.index)
f18.add_subplot(2,2,4)
sns.boxplot(x="GarageFinish", y="SalePrice", data=train, order = avg_price18_2.index)
plt.suptitle('Graphs of Non-numeric variables', size=23)
group_region19 = train.groupby('GarageQual')
avg_price19 = group_region19.aggregate({'SalePrice':np.mean}).sort_values('SalePrice', ascending = False)
group_region19_2 = train.groupby('GarageCond')
avg_price19_2 = group_region19_2.aggregate({'SalePrice':np.mean}).sort_values('SalePrice', ascending = False)
f19=plt.figure()
f19.add_subplot(2,2,1)
sns.stripplot(x="GarageQual", y="SalePrice", data=train, alpha=0.6,jitter=True, order = avg_price19.index)
f19.add_subplot(2,2,3)
sns.boxplot(x="GarageQual", y="SalePrice", data=train, order = avg_price19.index)
f19.add_subplot(2,2,2)
sns.stripplot(x="GarageCond", y="SalePrice", data=train, alpha=0.6,jitter=True, order = avg_price19_2.index)
f19.add_subplot(2,2,4)
sns.boxplot(x="GarageCond", y="SalePrice", data=train, order = avg_price19_2.index)
plt.suptitle('Graphs of Non-numeric variables', size=23)
f20=plt.figure()
f20.add_subplot(2,2,1)
sns.stripplot(x="PavedDrive", y="SalePrice", data=train, alpha=0.6,jitter=True)
f20.add_subplot(2,2,3)
sns.boxplot(x="PavedDrive", y="SalePrice", data=train)
f20.add_subplot(2,2,2)
sns.stripplot(x="PoolQC", y="SalePrice", data=train, alpha=0.6,jitter=True)
f20.add_subplot(2,2,4)
sns.boxplot(x="PoolQC", y="SalePrice", data=train)
plt.suptitle('Graphs of Non-numeric variables', size=23)
f21=plt.figure()
f21.add_subplot(2,2,1)
sns.stripplot(x="Fence", y="SalePrice", data=train, alpha=0.6,jitter=True)
f21.add_subplot(2,2,3)
sns.boxplot(x="Fence", y="SalePrice", data=train)
f21.add_subplot(2,2,2)
sns.stripplot(x="MiscFeature", y="SalePrice", data=train, alpha=0.6,jitter=True)
f21.add_subplot(2,2,4)
sns.boxplot(x="MiscFeature", y="SalePrice", data=train)
plt.suptitle('Graphs of Non-numeric variables', size=23)
group_region22 = train.groupby('SaleType')
avg_price22 = group_region22.aggregate({'SalePrice':np.mean}).sort_values('SalePrice', ascending = False)
group_region22_2 = train.groupby('SaleCondition')
avg_price22_2 = group_region22_2.aggregate({'SalePrice':np.mean}).sort_values('SalePrice', ascending = False)
f22=plt.figure()
f22.add_subplot(2,2,1)
sns.stripplot(x="SaleType", y="SalePrice", data=train, alpha=0.6,jitter=True, order = avg_price22.index)
f22.add_subplot(2,2,3)
sns.boxplot(x="SaleType", y="SalePrice", data=train, order = avg_price22.index)
f22.add_subplot(2,2,2)
sns.stripplot(x="SaleCondition", y="SalePrice", data=train, alpha=0.6,jitter=True, order = avg_price22_2.index)
f22.add_subplot(2,2,4)
sns.boxplot(x="SaleCondition", y="SalePrice", data=train, order = avg_price22_2.index)
plt.suptitle('Graphs of Non-numeric variables', size=23)
group_region23 = train.groupby('BsmtFinType1')
avg_price23 = group_region23.aggregate({'SalePrice':np.mean}).sort_values('SalePrice', ascending = False)
group_region23_2 = train.groupby('Foundation')
avg_price23_2 = group_region23_2.aggregate({'SalePrice':np.mean}).sort_values('SalePrice', ascending = False)
f23=plt.figure()
f23.add_subplot(2,2,1)
sns.stripplot(x="BsmtFinType1", y="SalePrice", data=train, alpha=0.6,jitter=True, order = avg_price23.index)
f23.add_subplot(2,2,3)
sns.boxplot(x="BsmtFinType1", y="SalePrice", data=train, order = avg_price23.index)
f23.add_subplot(2,2,2)
sns.stripplot(x="Foundation", y="SalePrice", data=train, alpha=0.6,jitter=True, order = avg_price23_2.index)
f23.add_subplot(2,2,4)
sns.boxplot(x="Foundation", y="SalePrice", data=train, order = avg_price23_2.index)
plt.suptitle('Graphs of Non-numeric variables', size=23)
m=[1,2,3,4,5]
n=[5,4,3,2,1]
ff=plt.figure()
#plt.scatter(n,m)
ff.add_subplot(2,1,1)
plt.scatter(m,n)
plt.tick_params(labelsize=5)
#labels = ax.get_xticklabels() + ax.get_yticklabels()
ff.add_subplot(2,1,2)
plt.scatter(n,n)
plt.suptitle('Graphs of Non-numeric variables', size=23)
数据预处理
## 查看数据相关属性
print('train数据集大小:',train.shape) # 1460*81 包含有目标变量“SalePrice”
#print('train数据集各变量数据类型:\n',train.dtypes) # 包含有字符串类型数据
print('test数据集大小:',test.shape) # 1459*80 不包含有目标变量,数据类型与train数据集相同
## 拼接相关数据集
data_0=pd.merge(test,sample,on='Id')
data=train.append(data_0) #m=data
## 查找非数值型数据 —— 查看是否有价格、时间等可转化为数值类型的数据
data_colnames_0=data.select_dtypes(include=['O']) #data数据集中非数值类型数据
data_colnames_1=data_colnames_0.columns #列名 不包含有时间类型数据
##统计原始数据集中各字符串类数据相关信息
Counts=[]
for i in range(len(data_colnames_1)):
counts={}
counts['列名']=data_colnames_1[i]
count=[]
for x in data_colnames_0[data_colnames_1[i]]:
if x not in count:
count.append(x)
counts['变量类型']=count
counts['变量类型数量']=len(count)
Counts.append(counts)
#Counts 原始数据集中各字符串类数据 包含的字符串种类
Counts_1=[]
#统计各字符串类数据 包含的字符串种类 及 次数
for i in range(len(data_colnames_1)):
counts={}
counts['列名']=data_colnames_1[i]
count={}
for x in data_colnames_0[data_colnames_1[i]]:
if x in count:
count[x] += 1
else:
count[x] = 1
counts['各类型数量']=count
Counts_1.append(counts)
#Counts_1 各字符串类数据 包含的字符串种类 及 次数
print('原数据集非数值类型变量统计:\n',Counts_1)
## 查找冗余数据
print('数据集中重复观测数据数:',data.duplicated().any()) #判断数据中是否存在有重复观测数据 不存在
#若存在,可使用‘drop_duplicates’删除重复观测数据,但是不影响原数据集,要删除原数据集中数据,需要将’inplace‘设置为True
#duplicated 和 drop_duplicates 都包含有参数“subset”,用于按指定变量做数据重复性判断
## 查找缺失值
#对数据行进行查找
data.isnull().any(axis=1).any() #判断数据行中是否包含有缺失值
print('原数据集数据行数:',data.shape[0])
print('包含有缺失值的数据行:',data.isnull().any(axis=1).sum()) #统计包含有缺失值的数据行数,都包含有缺失值
#对变量进行查找
data.isnull().any(axis=0) #判断各变量中是否包含有缺失值
data.isnull().sum(axis=0) #各变量中缺失值数量
print('各变量的缺失率:\n',data.isnull().sum(axis=0)/data.shape[0]) #各变量中缺失值比例
## 查找包含有缺失值的变量 并按照缺失率排序
miscount0=data.isnull().sum(axis=0)/data.shape[0] #计算缺失率
miscount1=pd.DataFrame(miscount0) #将‘Series’转化为‘DataFrame’格式
miscount1[1]=range(len(miscount0)) #给miscount添加序列
miscount=miscount1.sort_values(by=0,ascending=False) #排序
miscount.head(20) #所有缺失数据排序
m1=miscount[1][0:18] #数据集中缺失比率前19
m2=miscount[1][0:35] #记录含有缺失值的变量原有位置
m3=miscount[1][19:34] #数据集中缺失值小于等于2的变量
miscount_names=[]
data_colnames_2=data.columns #data数据集列名
for i in m2:
miscount_names.append(data_colnames_2[i])
#miscount_names 按照缺失率排序(从大到小)的变量名称
miscount_names_1=[]
for i in m1:
miscount_names_1.append(data_colnames_2[i])
#miscount_names_1 按照缺失率排序前19的变量名称
miscount_names_2=[]
for i in m3:
miscount_names_2.append(data_colnames_2[i])
#miscount_names_2 按照缺失率排序后16的变量名称
print('排序后的变量及其缺失率:\n',miscount.head(35))
print('按缺失率排序的变量:',miscount_names)
## 缺失值及异常值处理
#包含有缺失值变量的分析
#'PoolQC', 'MiscFeature', 'Alley', 'Fence', 'FireplaceQu', 'LotFrontage'
#‘泳池质量’ ‘其他类别的杂项特征’ ‘巷类型’ ‘围栏质量’ ‘壁炉质量’ ‘连接物业的街道线’
#缺失率前4(6)极高,考虑根据变量性质,对变量进行数值转换
# 'GarageYrBlt', 'GarageCond', 'GarageType', 'GarageFinish', 'GarageQual'
#‘车库建成年’,‘车库状况’,‘车库位置’,‘车库内饰’,‘车库质量’
#第7-11位都是有关于车库数据,且缺失率相同,可以考虑将缺失数据填补为0,表示无车库
#'BsmtFinType2', 'BsmtExposure'
#第12,13位‘ 第二成品区域的质量(如果存在)’ ,‘走道或花园式地下室墙’
#'BsmtQual', 'BsmtCond', 'BsmtFinType1'
#‘地下室高度’,‘地下室概况’,‘地下室竣工面积质量’
#第14-16位都是关于地下室数据,且缺失率相同,可以考虑将缺失数据填补为0,表示无车库
#'MasVnrArea', 'MasVnrType'
#第17,18位都是关于单板的数据,正常家庭都会有,应该是随机缺失变量,缺8个
#第19位以后缺失数据为 2或者1 应该是随机缺失变量
#观察包含有缺失值的变量数据集,寻找处理方法
misdata0=data[miscount_names] #包含有缺失值的数据集
# 所有非数值类型数据列名 data_colnames_1
# 所有包含有缺失值的变量名称 miscount_names
nonnumvalues=[]
for item in miscount_names:
if item in data_colnames_1:
nonnumvalues.append(item)
#nonnumvalues 筛选出包含有缺失值的非数值类型变量
numvalues=miscount_names
for item in nonnumvalues:
numvalues.remove(item)
#numvalues 筛选出包含有缺失值的数值类型变量 ['LotFrontage', 'GarageYrBlt', 'MasVnrArea']
misdata0.head(10)
# 各字符串类数据数据信息 Counts
# 各字符串类数据 包含的字符串种类 及 次数 Counts_1
nonnumvalues_count=[]
for i in range(len(Counts)):
if Counts_1[i]['列名'] in nonnumvalues:
nonnumvalues_count.append(Counts_1[i])
#nonnumvalues_count 含有缺失值的非数值类型变量的相关信息
data_colnames=pd.Series(data.columns) #包含有所有变量名称
#缺失值少于等于2个的变量,众数填充
#miscount_names_2 按照缺失率排序后16的变量名称
for item in miscount_names_2:
data[item].fillna(data[item].mode()[0],inplace=True)
#游泳池数据处理
print(data['PoolQC'].value_counts()) #输出'PoolQC'的分布情况
exdata_0=data[(data['PoolQC'].isnull())&(data['PoolArea']!=0)][['Id','PoolQC','PoolArea']]
print('存在有泳池面积却没有泳池质量的值:\n',exdata_0)
poolqc=data.groupby('PoolQC')['PoolArea'].mean() # 计算泳池质量的三个标准均值
data[2420:2421]['PoolQC'].fillna('Ex',inplace=True) # 根据距离各类指标平均面积距离填补
data[2503:2504]['PoolQC'].fillna('Fa',inplace=True)
data[2599:2600]['PoolQC'].fillna('Fa',inplace=True)
print('是否存在有泳池面积却没有泳池质量的值:\n',data[(data['PoolQC'].isnull())&(data['PoolArea']!=0)][['Id','PoolQC','PoolArea']])
exdata_1=data[(data['PoolQC'].notnull())&(data['PoolArea']==0)][['PoolQC','PoolArea']] #泳池数据的缺失是否同步
#exdata_q=data[(data['PoolQC'].notnull())&(data['PoolArea']!=0)][['PoolQC','PoolArea']] #查看有值的泳池数据同步的部分
data['PoolQC'].fillna('none',inplace=True)
print('PoolQC缺失值个数:',data['PoolQC'].isnull().sum(axis=0)) #无缺失值
#车库,同步缺失
Garage_list=data_colnames[data_colnames.str.contains('Garage')].values #包含有所有变量名中有‘Garage’的变量
#其中‘GarageArea’和‘GarageCars’是数值型数据,根据他们判断其余车库数据
data['GarageArea'].fillna(0,inplace=True)
data['GarageCars'].fillna(0,inplace=True)
#缺失非数值类数据填为‘none’,数值类型填补为0(或者其他可行值)
#data[(data['GarageArea']!=0)&(data['GarageCars']==0)]
#data[(data['GarageArea']==0)&(data['GarageCars']!=0)] #'GarageArea'和'GarageCars'同步
exdata_2=data[(data['GarageArea']==0)&(data['GarageCars']==0)]
print('车库数据之间是否同步',len(exdata_2)==data['GarageYrBlt'].isnull().sum(axis=0)) #判断是否同步缺失,不同步
exdata_2=data[(data['GarageCond'].isnull())&(data['GarageArea']!=0)][['Id','GarageCond','GarageArea','GarageCars']]
data=data[-data.Id.isin([2127])] #删除不同步行
# 替换'GarageCond', 'GarageType', 'GarageFinish', 'GarageQual'的缺失值为none
cara=['GarageCond','GarageType','GarageFinish','GarageQual']
for item in cara:
data[item].fillna('none',inplace=True)
data['GarageYrBlt'].fillna(min(data['GarageYrBlt']),inplace=True)
d0=data[['GarageCond','GarageType','GarageFinish','GarageQual','GarageYrBlt']].isnull().sum(axis=0) #无缺失值
print('车库数据缺失值统计',d0)
#地下室,同步缺失
Bsmt_list=data_colnames[data_colnames.str.contains('Bsmt')].values #包含有所有变量名中有‘Bsmt’的变量
exdata_3=data[(data['BsmtExposure'].isnull())&(data['BsmtCond'].notnull())] #'BsmtExposure'为空,'BsmtCond'不空
exdata_4=data[(data['BsmtExposure'].notnull())&(data['BsmtCond'].isnull())]
exdata_34=exdata_3.append(exdata_4)
exdata_34['BsmtExposure'].fillna(data['BsmtExposure'].mode()[0],inplace=True) #用众数填充
for a in range(len(exdata_34)):
#if data['Id']==exdata_34[a:a+1]['Id']:
m=int(exdata_34[a:a+1]['Id'])
data[m-1:m]['BsmtExposure']=exdata_34[a:a+1]['BsmtExposure']
#此时地下室缺失数据同步缺失,处理方法同车库
bsmt=['BsmtFinType2','BsmtExposure','BsmtQual','BsmtCond','BsmtFinType1']
for item in bsmt:
data[item].fillna('none',inplace=True)
d2=data[['BsmtFinType2','BsmtExposure','BsmtQual','BsmtCond','BsmtFinType1']].isnull().sum(axis=0) #无缺失值
#单板
exdata_5=data[(data['MasVnrArea'].isnull())&(data['MasVnrType'].isnull())]
len(exdata_5)==data['MasVnrArea'].isnull().sum(axis=0) #判断是否同步缺失
data['MasVnrType'].fillna('none',inplace=True)
data['MasVnrArea'].fillna(0,inplace=True)
d3=data[['MasVnrArea','MasVnrType']].isnull().sum(axis=0) #无缺失值
#异常值处理
#存在'MasVnrType'类型为“None",但是Area!=0的数据
exdata_6=data[(data['MasVnrType']=='None')&(data['MasVnrArea']!=0)][['MasVnrType','MasVnrArea']]
print('MasVnrArea的原始数据统计',Counts_1[17]) #'MasVnrArea'原始数据统计,存在none
data['MasVnrArea'][(data['MasVnrType']=='None')&(data['MasVnrArea']!=0)]=0
exdata_7=data[(data['MasVnrType']=='None')&(data['MasVnrArea']!=0)][['MasVnrType','MasVnrArea']] #异常值移除
#街道线
#考虑街道线填充空值不合适,所以通过相关关系进行填充
#此处使用Neighborhood(房屋附近位置)进行填充
data['LotFrontage']=data.groupby('Neighborhood')['LotFrontage'].transform(lambda x: x.fillna(x.median()))
print('LotFrontage的缺失值',data['LotFrontage'].isnull().sum(axis=0)) #无缺失值
#其余项填充
#'FireplaceQu' 壁炉质量
data['FireplaceQu'].fillna('none',inplace=True)
#'MiscFeature' 附加项
print(data['MiscFeature'].value_counts())
#data['MiscFeature'].fillna(data['MiscFeature'].mode()[0],inplace=True) #众数填充
data.drop(columns='MiscFeature',axis=1) #删去该变量
#'Alley' 巷类型
print(data['Alley'].value_counts())
data['Alley'].fillna('none',inplace=True) #填补为缺失值
#data.drop(columns='Alley',axis=1) #删去该变量
#'Fence' 围栏质量
print(data['Fence'].value_counts())
#data['Fence'].fillna('none',inplace=True) #填补为缺失值
data.drop(columns='Fence',axis=1) #删去该变量
## 数据保存
#data.to_csv('C:\\Users\\Lenoovo\\Desktop\\housing\\data_1.csv')
##拆分数据集
train=data[0:1460]
text=data[1460:2918]
建模
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
plt.rcParams['font.sans-serif'] = ['SimHei'] # 绘图时可以显示中文
plt.rcParams['axes.unicode_minus']=False # 绘图时显示负号
warnings.filterwarnings("ignore") # 不要显示警告
# 读取数据预处理后的数据
data= pd.read_csv('C:/Users/91333/Documents/semester6/data science/期末/data_1.csv')
data = data.drop(["Id","Unnamed: 0"],axis=1)
# 特征工程
# SalePrice的分布分析
from scipy import stats
from scipy.stats import norm,skew
# data['SalePrice'][:1460].describe()
# #histogram画直方图,且查看数据是否符合正态分布
# sns.distplot(data['SalePrice'][:1460],fit=norm)# 直方图和正态概率图
# (mu, sigma) = norm.fit(data['SalePrice'][:1460])# Get the fitted parameters used by the function
# plt.legend(['Normal dist. ($\mu=$ {:.2f} and $\sigma=$ {:.2f} )'.format(mu, sigma)],
# loc='best')
# plt.ylabel('Frequency')
# plt.title('SalePrice distribution')
# fig = plt.figure()
# res = stats.probplot(data['SalePrice'][:1460], plot=plt)
# plt.show() ## 由图像可知,图像的非正态分布
# print("Skewness: %f" %data['SalePrice'].skew()) #偏度
# print("Kurtosis: %f" %data['SalePrice'].kurt()) #峰度
# 所以要变换一下,log1p变换
data['SalePrice'] = np.log1p(data['SalePrice'])
# 在绘制直方图看一下
# sns.distplot(data['SalePrice'][:1460],fit=norm )
# (mu, sigma) = norm.fit(data['SalePrice'][:1460])
# plt.legend(['Normal dist. ($\mu=$ {:.2f} and $\sigma=$ {:.2f} )'.format(mu, sigma)],
# loc='best')
# plt.ylabel('Frequency')
# plt.title('SalePrice distribution')
# fig = plt.figure()
# res = stats.probplot(data['SalePrice'][:1460], plot=plt)
# plt.show()
# print("Skewness: %f" %data['SalePrice'].skew()) #偏度
# print("Kurtosis: %f" %data['SalePrice'].kurt()) #峰度
# # 和前边偏度峰度对比,发现处理之后的偏度峰度都减小了
‘’’K-S检验python没有现成的函数,为了效率用了R,担待担待。
ks.test(data$SalePrice,pnorm,mean(data$SalePrice), sd(data$SalePrice))
ks.test(log(data$SalePrice+1),mean(log(data$SalePrice+1)), sd(log(data$SalePrice+1)))
‘’’
# # 回归训练集和测试集
numeric_feats = data.dtypes[data.dtypes != "object"].index
# Check the skew of all numerical features
skewed_feats = data[numeric_feats].apply(lambda x: skew(x.dropna())).sort_values(ascending=False)
#print("\nSkew in numerical features: \n")
skewness = pd.DataFrame({'Skew' :skewed_feats})
#skewness.head(10)
skewness = skewness[abs(skewness) > 0.75]
#print("There are {} skewed numerical features to Box Cox transform".format(skewness.shape[0]))
from scipy.special import boxcox1p
skewed_features = skewness.index
lam = 0.15 # lam = 0.15 y=((1+x)**lam-1)/lam if lam=0,y=log(1+x)
for feat in skewed_features:
data[feat] = boxcox1p(data[feat], lam)
# 哑变量
data = pd.get_dummies(data)
print(data.shape)
# 切回训练集和测试集
X_train = data[:1460].drop("SalePrice",axis=1)
X_test = data[1460:].drop("SalePrice",axis=1)
y_train = data[:1460].SalePrice.values
y_test = data[1460:].SalePrice.values
# 拟合模型
# 指标 Validation function
from sklearn.model_selection import cross_val_score,KFold
from sklearn.metrics import mean_squared_error
n_folds = 5
def rmsle_cv(model):
kf = KFold(n_folds, shuffle=True, random_state=42).get_n_splits(X_train.values)
rmse= np.sqrt(-cross_val_score(model, X_train.values, y_train, scoring="neg_mean_squared_error", cv = kf))
return(rmse)
'''
#linear models
from sklearn.linear_model import ElasticNetCV, LassoCV, RidgeCV,LinearRegression
score = rmsle_cv(LinearRegression())
print("linear Regression rmse: {:.4f} ({:.4f})\n".format(score.mean(), score.std())) #非常大,要进行变量选择等
score = rmsle_cv(LassoCV(cv=5, random_state=0, max_iter=10000))
print("Lasso rmse: {:.4f} ({:.4f})\n".format(score.mean(), score.std()))
score = rmsle_cv(ElasticNetCV(cv=5,random_state=0))
print("ElasticNet rmse: {:.4f} ({:.4f})\n".format(score.mean(), score.std()))
score = rmsle_cv(RidgeCV(cv=5))
print("ridge rmse: {:.4f} ({:.4f})\n".format(score.mean(), score.std()))
'''
# 核方法,KernelRidge和SVR
from sklearn.kernel_ridge import KernelRidge
from sklearn.svm import SVR,LinearSVR
'''
#SVR
#线性核
#SVR函数:效果不好rmse最小,为0.0324133,不符合常理。
C_range = [0.00001,0.0001,0.001,0.01,0.1,1,10,100]
linearSVR_cv_scores = []
for c in C_range:
svr = SVR(C=c)
scores = rmsle_cv(svr)
linearSVR_cv_scores.append(scores.mean())
print('SVR中当松弛变量C取{}时,rmse最小,为{}\n'.format( C_range[linearSVR_cv_scores.index(min(linearSVR_cv_scores))],min(linearSVR_cv_scores)))
plt.figure(figsize=(10,4))
plt.plot(C_range,linearSVR_cv_scores)
plt.xlabel("C")
plt.ylabel("rmse")
plt.title("SVR函数rmse随惩罚系数C变化图")
plt.show()
#LinearSVR函数 更适合大样本,胜出。
linearSVR_cv_scores = []
for c in C_range:
svr = LinearSVR(C=c)
scores = rmsle_cv(svr)
linearSVR_cv_scores.append(scores.mean())
print('LinearSVR中当松弛变量C取{}时,rmse最小,为{}\n'.format( C_range[linearSVR_cv_scores.index(min(linearSVR_cv_scores))],min(linearSVR_cv_scores)))
plt.figure(figsize=(10,4))
plt.plot(C_range,linearSVR_cv_scores)
plt.xlabel("C")
plt.ylabel("rmse")
plt.title("LinearSVR函数rmse随惩罚系数C变化图")
plt.show()
#高斯核 由于存在两个参数松弛变量C和gamma,进行网格搜索。
rbfSVR_cv_scores = pd.DataFrame()
i=0
for c in C_range:
for Gamma in [0.0001,0.001,0.01,0.1,1,10]: rbfSVR_cv_scores[i]=[c,Gamma,rmsle_cv(SVR(kernel="rbf",C=c,gamma=Gamma)).mean()]
i=i+1
print('高斯核SVR:c={},gamma={}时,rmse最小为{}\n'.format(rbfSVR_cv_scores.iloc[:,rbfSVR_cv_scores.iloc[2,].argmin()][0], rbfSVR_cv_scores.iloc[:,rbfSVR_cv_scores.iloc[2,].argmin()][1], rbfSVR_cv_scores.iloc[:,rbfSVR_cv_scores.iloc[2,].argmin()][2]))
rbfSVR_cv_scores = rbfSVR_cv_scores.T
rbfSVR_cv_scores.columns = ["C","gamma","rmse"]
sns.relplot(data=rbfSVR_cv_scores,x="C",y='rmse',kind='line',hue='gamma',col='gamma')
plt.show()
# 多项式核函数 存在三个参数 松弛变量C、gamma和阶数,网格搜索
ploySVR_cv_scores = pd.DataFrame()
i=0
for c in [0.01,0.1,1]:
for Degree in [1,2,3]:
for Gamma in [0.00000001,0.0000000001,0.000000001,1/302]: ploySVR_cv_scores[i]=[c,Degree,Gamma,rmsle_cv(SVR(kernel="poly",C=c,degree=Degree,gamma=Gamma)).mean()]
i=i+1
print(ploySVR_cv_scores.iloc)
print('多项式SVR:c={},degree={}时,gamma={}时,rmse最小为{}\n'.format(ploySVR_cv_scores.iloc[:,ploySVR_cv_scores.iloc[3,].argmin()][0], ploySVR_cv_scores.iloc[:,ploySVR_cv_scores.iloc[3,].argmin()][1], ploySVR_cv_scores.iloc[:,ploySVR_cv_scores.iloc[3,].argmin()][2], ploySVR_cv_scores.iloc[:,ploySVR_cv_scores.iloc[3,].argmin()][3]))
#KernelRidge
#线性核
alpha_range=[0.00001,0.0001,0.001,0.01,0.1,1,3,5,10,100]
linearkrr_cv_scores = []
for Alpha in alpha_range:
krr = KernelRidge(alpha = Alpha)
scores = rmsle_cv(krr)
linearkrr_cv_scores.append(scores.mean())
print('线性核krr中当松弛变量alpha取{}时,mse最小,为{}\n'.format( alpha_range[linearkrr_cv_scores.index(min(linearkrr_cv_scores))],min(linearkrr_cv_scores)))
plt.figure(figsize=(10,4))
plt.plot(alpha_range,linearkrr_cv_scores)
plt.xlabel("alpha")
plt.ylabel("rmse")
plt.title("krr函数rmse随惩罚系数alpha变化图")
plt.show()
#高斯核 由于存在两个参数松弛变量alpha和gamma,进行网格搜索。
rbfkrr_cv_scores = pd.DataFrame()
i=0
for Alpha in alpha_range:
for Gamma in [0.000001,0.0000001,0.0005]: rbfkrr_cv_scores[i]=[Alpha,Gamma,rmsle_cv(KernelRidge(kernel="rbf",alpha=Alpha,gamma=Gamma)).mean()]
i=i+1
print('高斯核krr:alpha={},gamma={}时,rmse最小为{}\n'.format(rbfkrr_cv_scores.iloc[:,rbfkrr_cv_scores.iloc[2,].argmin()][0], rbfkrr_cv_scores.iloc[:,rbfkrr_cv_scores.iloc[2,].argmin()][1], rbfkrr_cv_scores.iloc[:,rbfkrr_cv_scores.iloc[2,].argmin()][2]))
'''
# 多项式核函数 存在两个参数 松弛变量C和阶数,网格搜索
ploykrr_cv_scores = pd.DataFrame()
i=0
for Alpha in [0.001,0.01,0.1,0.4,1]:
for Degree in [1,2,3]:
for Gamma in [0.00000001,0.0000000001,0.000000001,1/302]:
ploykrr_cv_scores[i]=[Alpha, Degree, Gamma, rmsle_cv(KernelRidge(kernel="poly",alpha=Alpha,degree=Degree,gamma=Gamma)).mean()]
i=i+1
print('多项式核krr:alpha={},degree={}时,gamma={}时,rmse最小为{}\n'.format(ploykrr_cv_scores.iloc[:,ploykrr_cv_scores.iloc[3,].argmin()][0], ploykrr_cv_scores.iloc[:,ploykrr_cv_scores.iloc[3,].argmin()][1], ploykrr_cv_scores.iloc[:,ploykrr_cv_scores.iloc[3,].argmin()][2], ploykrr_cv_scores.iloc[:,ploykrr_cv_scores.iloc[3,].argmin()][3]))
ploykrr_cv_scores = pd.DataFrame()
i=0
for Alpha in [0.001,0.01,0.1,0.4,1]:
for Degree in [1,2,3]:
ploykrr_cv_scores[i]=[Alpha, Degree,rmsle_cv(KernelRidge(kernel="poly",alpha=Alpha,degree=Degree)).mean()]
i=i+1
print('多项式核krr:alpha={},degree={}时,rmse最小为{}\n'.format(ploykrr_cv_scores.iloc[:,ploykrr_cv_scores.iloc[2,].argmin()][0], ploykrr_cv_scores.iloc[:,ploykrr_cv_scores.iloc[2,].argmin()][1], ploykrr_cv_scores.iloc[:,ploykrr_cv_scores.iloc[2,].argmin()][2]))
#分布分析
##随机梯度下降法(SGD)是一种在线性支持向量机和Logistic回归等凸损失函数下拟合线性分类器和回归器的简单而有效的方法。
#from sklearn.linear_model import SGDRegressor
#clf = SGDRegressor(loss="squared_loss", penalty="l2", max_iter=5) #loss损失参数,"squared_loss"适合线性回归
##penalty="l2": L2 norm penalty on coef_.
##penalty="l1": L1 norm penalty on coef_.
##penalty="elasticnet": Convex combination of L2 and L1; (1 - l1_ratio) * L2 + l1_ratio * L1. 就是ElasticNet
##默认设置为pension=“l2”。L1惩罚导致稀疏解,使大多数系数为零。
##弹性网11解决了在存在高度相关属性的情况下L1惩罚的一些缺陷。参数l1_比率控制l1和L2惩罚的凸组合。
#score = rmsle_cv(clf)
#print("clf score: {:.4f} ({:.4f})\n".format(score.mean(), score.std()))
#多元线性回归
from sklearn.linear_model import LinearRegression
reg=LinearRegression()
reg.fit(X_train,y_train)
score = rmsle_cv(reg)
print("regr score: {:.4f} ({:.4f})\n".format(score.mean(), score.std())) #非常大,要进行变量选择等
#多层感知器回归器
from sklearn.neural_network import MLPRegressor
for i in range(450,501):
regr = MLPRegressor(max_iter=i).fit(X_train, y_train)
print('最大深度={},mse均值:{:.3f}'.format(i,rmsle_cv(regr).mean()))
regr = MLPRegressor(max_iter=500).fit(X_train, y_train)
#activation为tanh效果最好 f(x) = tanh(x)
#500时已经收敛
score = rmsle_cv(regr)
print("regr score: {:.4f} ({:.4f})\n".format(score.mean(), score.std()))
#参数调整
#随机搜索
from sklearn.model_selection import RandomizedSearchCV
solver = ['lbfgs','sgd','adam']#优化算法
neu=[]
for i in range(0,100):
for j in range(0,100):
for k in range(0,100):
neu.append((i,j,k))
distributions = dict(hidden_layer_sizes=neu,solver=solver,activation=['identity','logistic','tanh','relu'])
rscv=RandomizedSearchCV(regr,distributions, random_state=0)
search = rscv.fit(X_test, y_test)
search.best_params_
regr1 = MLPRegressor(hidden_layer_sizes=(73, 83, 68),solver='lbfgs',max_iter=500,activation='identity').fit(X_train, y_train)
score = rmsle_cv(regr1)
print("regr score: {:.4f} ({:.4f})\n".format(score.mean(), score.std())) #0.0192 (0.0015)
#只用robu 0.0161 (0.0014)
#+变量选择 0.0192 0.0030
#决策树
from sklearn.tree import DecisionTreeRegressor
tree = DecisionTreeRegressor(max_depth=2).fit(X_train,y_train) #最大深度
score = rmsle_cv(tree)
print("tree score: {:.4f} ({:.4f})\n".format(score.mean(), score.std()))
for i in range(1,10):
treei=DecisionTreeRegressor(max_depth=i).fit(X_train,y_train)
print('最大深度={},mse均值:{:.3f}'.format(i,rmsle_cv(treei).mean()))
#6最小,7又变大了
tree6= DecisionTreeRegressor(max_depth=6).fit(X_train,y_train) #最大深度
score = rmsle_cv(tree6)
print("tree score: {:.4f} ({:.4f})\n".format(score.mean(), score.std())) #robu 0.0221 0.0009
#+变量选择 0.0225 0.0012
#BaggingRegressor,是一个Bagging的回归器组合,用于集成多个回归器。
from sklearn.svm import SVR
from sklearn.ensemble import BaggingRegressor
bgr = BaggingRegressor(base_estimator=SVR(),n_estimators=4,random_state=0).fit(X_train, y_train)
score = rmsle_cv(bgr)
print("SVR_bagging score: {:.4f} ({:.4f})\n".format(score.mean(), score.std()))
#for i in range(1,20): #要集成的基估计器的个数
# regri=BaggingRegressor(base_estimator=SVR(),n_estimators=i,random_state=0).fit(X_train, y_train)
# print('n_estimators={},mse均值:{:.3f}'.format(i,rmsle_cv(regri).mean()))
#Bagging_随机森林
bgr = BaggingRegressor(n_estimators=7,random_state=0).fit(X_train, y_train) #base_estimator默认为决策树,此时构成随机森林
score = rmsle_cv(bgr)
print("tree_bagging score: {:.4f} ({:.4f})\n".format(score.mean(), score.std()))
#for i in range(1,20): #要集成的基估计器的个数
# regri=BaggingRegressor(n_estimators=i,random_state=0).fit(X_train, y_train)
# print('n_estimators={},mse均值:{:.3f}'.format(i,rmsle_cv(regri).mean()))
clf = BaggingRegressor().fit(X_train, y_train)
ne=[]
for i in range(0,20):
ne.append(i)
distributions = dict(base_estimator=[SVR(),DecisionTreeRegressor(),MLPRegressor(),LassoCV(),ElasticNetCV(),RidgeCV()],n_estimators=ne)
rscv=RandomizedSearchCV(clf,distributions, random_state=0)
search = rscv.fit(X_test, y_test)
search.best_params_
bgr = BaggingRegressor(base_estimator=ElasticNetCV(cv=5,random_state=0),n_estimators=14,random_state=0).fit(X_train, y_train)
score = rmsle_cv(bgr)
print("en_bagging score: {:.4f} ({:.4f})\n".format(score.mean(), score.std()))
#Stacked generalization
#每个单独估计器的预测被叠加在一起,作为最终估计器的输入来计算预测。最后的估计器是通过交叉验证来训练的。
from mlxtend.regressor import StackingRegressor
estimators=[SVR(),DecisionTreeRegressor(),MLPRegressor(),LassoCV(),ElasticNetCV(),RidgeCV()]
reg = StackingRegressor(regressors=estimators,meta_regressor=RidgeCV()).fit(X_train,y_train)
score = rmsle_cv(reg)
print("reg: {:.4f} ({:.4f})\n".format(score.mean(), score.std())) #全en 0.0243 (0.0020) ridge0.0183 (0.0017)
del(estimators[2])
reg = StackingRegressor(regressors=estimators,meta_regressor=MLPRegressor()).fit(X_train,y_train)
score = rmsle_cv(reg)
print("reg: {:.4f} ({:.4f})\n".format(score.mean(), score.std())) #全 0.0404 (0.0026)
for i in range(0,len(estimators)): stimatorss=[SVR(),DecisionTreeRegressor(),MLPRegressor(),LassoCV(),ElasticNetCV(),RidgeCV()]
del(estimatorss[i])
reg = StackingRegressor(regressors=estimatorss,meta_regressor=estimators[i]).fit(X_train,y_train)
score = rmsle_cv(reg)
print("方法是={},mse均值:{:.3f}\n".format(estimators[i],score.mean()))
变量选择算法尝试
y = all_data["SalePrice"]
x = all_data.drop(data_colnames_1,axis=1)
base_estimator = Pipeline([
('scaler', StandardScaler()),
('model', LogisticRegression(penalty='l1'))
])
## Here stability selection is instantiated and run
selector1 = StabilitySelection(base_estimator=base_estimator, lambda_name='model__C',
lambda_grid=np.logspace(-5, -1, 50)).fit(x, y.astype('int'))
print(selector1.get_support(indices=True))
n=selector1.get_support(indices=True)
features=[]
for i in n:
feature=x.columns[i]
features.append(feature)
#选择结果
#MSSubClass: The building class
#LotFrontage: Linear feet of street connected to property
#LotArea: Lot size in square feet
#OverallQual: Overall material and finish quality
#OverallCond: Overall condition rating
#YearBuilt: Original construction date
#MasVnrArea: Masonry veneer area in square feet
#BsmtFinSF1: Type 1 finished square feet
#1stFlrSF: First Floor square feet
#GrLivArea: Above grade (ground) living area square feet
#HalfBath: Half baths above grade
#Bedroom: Number of bedrooms above basement level
#Kitchen: Number of kitchens
#TotRmsAbvGrd: Total rooms above grade (does not include bathrooms)
#GarageYrBlt: Year garage was built
#OpenPorchSF: Open porch area in square feet
#EnclosedPorch: Enclosed porch area in square feet
#MoSold: Month Sold
#YrSold: Year Sold
selector2 = StabilitySelection(base_estimator=base_estimator,
lambda_name='model__C',
lambda_grid=np.logspace(-5, -1, 50),
bootstrap_func='complementary_pairs')
selector2.fit(x, y.astype('int'))
print(selector2.get_support(indices=True))
#
from sklearn.feature_selection import RFE
from sklearn.linear_model import LinearRegression
names = x.columns.values.tolist()
#use linear regression as the model
lr = LinearRegression()
#rank all features, i.e continue the elimination until the last one
rfe = RFE(lr, n_features_to_select=1)
rfe.fit(x,y.astype('int'))
print("Features sorted by their rank:")
print(sorted(zip(map(lambda x: round(x, 4), rfe.ranking_), names))