Tensorflow笔记——第一讲 神经网络计算（1.1 1.2 1.3）

1.1人工智能学派

行为主义

基于控制论，构建感知-动作控制系统（如平衡、行走、避障等自适应控制系统）

符号主义

基于算术逻辑表达式，求解问题先把问题描述为表达式，再求解表达式（可用公式表示，实现理性思维）

连接主义

仿生学，模仿神经元连接关系（仿脑神经元连接，实现感性思维）

1.2神经网络设计过程

准备数据

采集大量（特征，标签）数据

搭建网络

搭建神经网络结构

优化参数

优化连接的权重，训练网络获取最佳参数（反向传播）

应用网络

将网络保存为模型，输入新数据，输出分类或预测结果（前向传播）

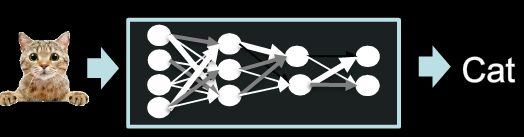
Examples：用神经网络实现鸢尾花分类

前向传播

y0 = x0 * w0,0 + x1 * w1,0 + x2 * w2,0 + x3 * w3,0 + b0 =  1.01
y1和y2依次类推

损失函数
Attention：损失函数有很多种定义的方法，吴恩达ML视频中的定义如下
Loss function（单个训练样本）：L（y, y_） = -(y_logy + (1-y_)log(1-y))

反向传播
·梯度：函数对各参数求偏导后的向量
·梯度下降法：沿损失函数梯度下降的方向，寻找损失函数的最小值，得到最优参数的方法
·学习率（learning rate）:设置过小，收敛过程会十分缓慢；设置过大，可能会在最小值附近来回震荡，甚至无法收敛

1.3张量生成

张量的定义

·张量：多维数组（列表）
·阶：张量的维数

维数	阶	名字	例子
0-D	0	标量scalar	s = 123
1-D	1	向量vector	v = [1,2,3]
2-D	2	矩阵matrix	m = [[1,2,3], [4,5,6], [7,8,9]]
n-D	n	tensor	t = [[[…[(n个左括号)

数据类型

·tf.int, tf.float
tf.int32, tf.float32, tf.float64

·tf.bool
tf.constant([True, False])

·tf.string
tf.constant(“Hello, world!”)

如何创建一个Tensor

创建一个张量

import tensorflow as tf

a = tf.constant([1, 5], dtype=tf.int64)
print("a:", a)
print("a.dtype:", a.dtype)
print("a.shape:", a.shape)

运行结果：
a: tf.Tensor([1 5], shape=(2,), dtype=int64)
a.dtype: <dtype: 'int64'>
a.shape: (2,)

注意：a是一个一维向量，而不是一个只有一行的矩阵

将numpy的数据类型转换成Tensor数据类型

import tensorflow as tf
import numpy as np

a = np.arange(0, 5)
b = tf.convert_to_tensor(a, dtype=tf.int64)
print("a:", a)
print("b:", b)

运行结果：
a: [0 1 2 3 4]
b: tf.Tensor([0 1 2 3 4], shape=(5,), dtype=int64)

创建全为0/1/指定值的张量

import tensorflow as tf

a = tf.zeros([2, 3])
b = tf.ones(4)
c = tf.fill([2, 2], 9)
print("a:", a)
print("b:", b)
print("c:", c)

运行结果：
a: tf.Tensor(
[[0. 0. 0.]
 [0. 0. 0.]], shape=(2, 3), dtype=float32)
b: tf.Tensor([1. 1. 1. 1.], shape=(4,), dtype=float32)
c: tf.Tensor(
[[9 9]
 [9 9]], shape=(2, 2), dtype=int32)

注意：一维直接写个数，二维用[行，列]，多维用[n,m,j,k…]

生成正态分布的随机数，默认均值为0，标准差为1

import tensorflow as tf

d = tf.random.normal([2, 2], mean=0.5, stddev=1)
print("d:", d)
//tf.random.truncated_normal生成截断式正态分布的随机数
e = tf.random.truncated_normal([2, 2], mean=0.5, stddev=1)
print("e:", e)

运行结果：
d: tf.Tensor(
[[0.9602163  0.91875494]
 [2.5410552  0.89230907]], shape=(2, 2), dtype=float32)
e: tf.Tensor(
[[2.291284   0.9167075 ]
 [0.58420265 0.05498555]], shape=(2, 2), dtype=float32)

生成均匀分布随机数

import tensorflow as tf
//tf.random.uniform(维度,minval=最小值,maxval=最大值)
f = tf.random.uniform([2, 2], minval=0, maxval=1)
print("f:", f)

运行结果：
f: tf.Tensor(
[[0.3601756  0.70198834]
 [0.04205799 0.5456892 ]], shape=(2, 2), dtype=float32)