6.2 树和二叉树-二叉树的存储结构及遍历

1、二叉树的存储结构

1.1、顺序存储结构

#define MAX_TREE_SIZE 100 // 二叉树的最大结点数
typedef int TElemType;
typedef TElemType SqBiTree[MAX_TREE_SIZE]; // 0号单元存储根结点
SqBiTree bt;

1.2、二叉链表存储结构

typedef struct BiTNode{
	TElemType data;
	struct BiTNode * lchild, * rchild;
} BiTNode, * BiTree;

1.3、三叉链表存储结构

typedef struct TriTNode{
	TElemType data;
	struct TriTNode * lchild, * rchild;
	struct TriTNode * parent;
} TriTNode, * TriTree;

1.4、双亲链表存储结构

typedef struct BiPTNode{
	TElemType data;
	int * parent;
	char LRTag;
}BiPTNode;

typedef struct BiPTree{
	BiPTNode nodes[MAX_TREE_SIZE];
	int num_node;
	int root;
}BiPTree;

2、二叉树的遍历(图解)

2.1 先序遍历：[先访问根节点]

先访问根节点，再先序访问左子树，再先序访问右子树

2.2 中序遍历：[中间访问根节点]

先中序遍历左子树，再访问根节点，再中序遍历右子树

2.3 后序遍历：[最后访问根节点]

先中序遍历左子树，再中序遍历右子树，再访问根节点

2.4 已知两种遍历序列求原始二叉树

通过【先序和中序】 或者 【中序和后序】 我们可以还原出原始的二叉树。
但通过【先序和后序】是无法还原出原始的二叉树的。

---

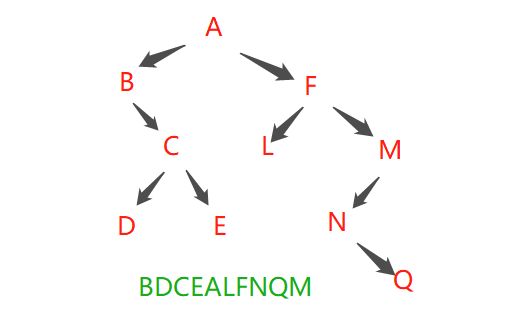
示例1：已知，先序：ABCDEFGH, 中序:BDCEAFHG, 求后序。
答案：DECBHGFA（需要先根据先序和中序画出原始二叉树）。

---

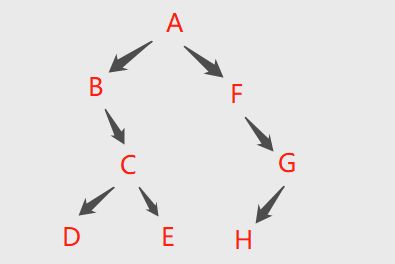
示例2：已知，先序：ABDGHCEFI, 中序: GDHBAECIF, 求后序。
答案：GHDBEIFCA（需要先根据先序和中序画出原始二叉树）。

---

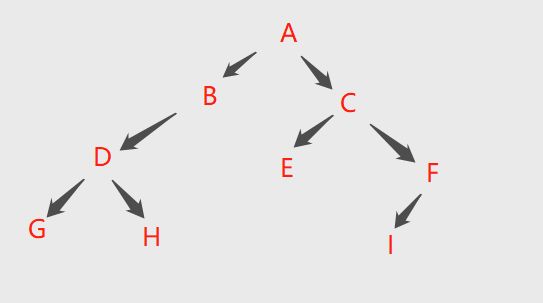
示例3：已知，中序：BDCEAFHG, 后序序:DECBHGFA, 求先序。
答案：ABCDEFGH（需要先根据中序和后序画出原始二叉树）。

---

3、二叉树的遍历(代码)

3.1、递归遍历二叉树描述

	//先序遍历二叉树
	/*
	采用二叉链表存储结构，Visit是对数据元素操作的应用函数
	先序遍历二叉树T的递归算法，对每个数据元素调用函数Visit。
	最简单的Visit函数是：
	Status PrintElement(TElemType e){// 输出e的值
		printf(e);					 // 使用时，加上格式串
		return OK;
	}
	// 调用实例：PreOrder(T, PrintElement);
	*/
void PreOrder(BiTree T, void (*visit)(TElemType &e)){
	if(T){
		visit(T->data); //访问结点
		PreOrder(T->lchild, visit); //遍历左子树
		PreOrder(T->rchild, visit); //遍历右子树
	}
} //PreOrder

3.2、非递归遍历二叉树描述

// 非递归中序遍历二叉树 -- start
BiTNode * GoFarLeft(BiTree T, Stack * S){
	if(!T){
		return NULL;
	}
	while(T->lchild){
		Push(S, T);
		T = T->lchild;
	}
	return T;
}
void InOrderNonRecursive(BiTree T, void (* visit)(TElemType &e)){
	Stack * S;
	BiTNode * t = GoFarLeft(T, S);// 找到最左下的结点
	while(t){
		visit(t->data);
		if(t->rchild){// 
			t = GoFarLeft(t->rchild, S);
		}else if(!StackEmpty(S)){ // 栈不空时退栈
			t = Pop(S);
		}else{// 栈空表明遍历结束
			t = NULL;
		}
	}
}

4、遍历的应用

4.1、统计二叉树中叶子结点的个数(递归先序遍历)

void CountLeaf(BiTree T, int &count){
	if(T){
		if((!T->lchild) && (!T->rchild)){
			count++;
		}
		CountLeaf(T->lchild, count); 
		CountLeaf(T->rchild, count);
	}
}

4.2、求二叉树的深度(后序遍历)

$\begin{array}{rl}& 二叉树的深度=Max\{左子树的深度,右子树的深度\}+1\\ & depth=Max\{d_l,d_r\}+1\end{array}$

int Depth(BiTree T){
	if(!T){
		depthVal = 0;
	}else{
		depthLeft = Depth(T->lchild);
		depthRight = Depth(T->rchild);
		depthVal = 1 + (depthLeft > depthRight ? depthLeft : depthRight);
	}
	return depthVal;
}

4.3、复制二叉树(后序遍历)

//生成一个二叉树的结点
BiTNode * GetTreeNode(TElemType item, BiTNode *lptr, BiTNode *rptr){
	T = (BiTNode *)malloc(sizeof(BiTNode));
	if(!T){
		exit(1);
	}
	T->data = item;
	T->lchild = lptr;
	T->rchild = rptr;
	return T;
}

BiTNode *CopyTree(BiTNode *T){
	if(!T){
		return NULL;
	}
	if(T->lchild){
		newlptr = CopyTree(T->lchild);
	}else{
		newlptr = NULL;
	}
	if(T->rchild){
		newrptr = CopyTree(T->rchild)
	}else{
		newrptr = NULL;
	}
	newnode = GetTreeNode(T->data, newlptr, newrptr);
	return newnode;
}

4.4、按给定的先序序列建立二叉树

暂定：
空树用 “ ”
“根” “左子树” “右子树”
按给定的添加空格的完整的先序序列建立二叉树

Status CreateBiTree(BiTree &T){
	scanf(&ch);
	if(ch == ' '){
		T = NULL;
	}else{
		T = (BiTNode *)malloc(sizeof(BiTNode));
		if(!T){
			exit(OVERFLOW);
		}
		T->data = ch; //生成根结点
		CreateBiTree(T->lchild); //构造左子树
		CreateBiTree(T->rchild); //构造右子树
	}
	return OK;
} //CreateBiTree

4.5、由表达式序列建立二叉树

由先缀表示式建树
例如：已知表达式的先缀表示式$-\times +abc/de$

1 带空格的表达式序列建二叉树
2 先序表达式 后序表达式 建立二叉树
3 原表达式 建立二叉树

原表达式 建立二叉树
void CrtExpTree(BiTree &T, char exp[]){
	InitStack(S); //运算符栈
	Push(S, '#');
	InitStack(PTR); //操作数栈
	p = exp;
	ch = *p;
	while(!(GetTop(S) == '#' && ch == '#')){
		if(!IN(ch, OP)){ //ch不是运算符
			CrtNode(t, ch); //建叶子结点并入栈
		}else{ //ch是运算符
			switch(ch){
				case '(': 
					Push(S, ch);
					break; //
				case ')':
					Pop(S, c);
					while(c != '('){
						CrtSubTree(t, c);//建二叉树并入栈
						Pop(S, c);
					}
					break;
				default: 
					while(!GetTop(S, c)&& (Precede(c, ch))){
						CrtSubTree(t, c);
						Pop(S, c);
					}
					if(ch != '#'){
						Push(S, ch);
					}
					break;// default
			}// switch
		}// else
		if(ch != '#'){
			p++;
			ch = *p;
		}
	}// while
	Pop(PTR, T);
} //CrtExpTree

//建叶子结点的算法为:
void CrtNode(BiTree &T, char ch){
	T = (BiTNode *)malloc(sizeof(BiTNode));
	T->data = ch;
	T->lchild = T->rchild = NULL;
	Push(PTR, T);
}


//建子树的算法为:
void CrtSubTree(BiTree& T, char c){
	T = (BiTNode *)malloc(sizeof( BiTNode));
	T->data = c;
	Pop(PTR, rc);
	T->rchild = rc;
	Pop(PTR, lc);
	T->lchild = lc;
	Push(PTR, T);
}

4.6、由二叉树的先序和中序序列建树

中序：左子树 根 右子树
先序：根 …
后序：… 根

例如:已知二叉树的
先序序列:abcdefg
中序序列:cdbaegf
分析可得:
根结点是 a
左子树是 cdb
右子树是 egf

=========================================================================

typedef enum PointerTag {Link, Thread};// Link==0指针, Thread==1线索
typedef int TElemType;

//线索链表，线索二叉树，线索化
typedef struct BiThrNode{
	TElemType data;
	struct BiThrNode * lchild, * rchild;//左右孩子指针
	PointerTag LTag, RTag;// 左右标志
}BiThrNode, * BiThrTree;

// 4、线索链表存储结构