CS231n: Lecture 9 | CNN Architectures Summary

Lecture 9主要讲了一些经典的、比较流行的网络结构，详细讲解了AlexNet、ZFNet、VGGNet、GoogleNet和ResNet。

AlexNet

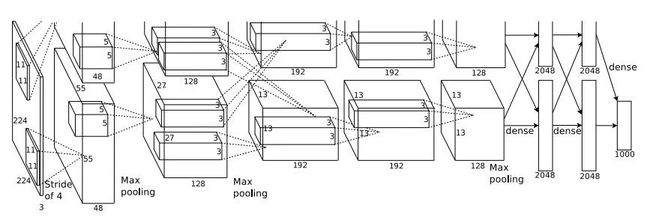
AlexNet网络结构图如下图所示：

网络详细信息如下

[227x227x3] INPUT
[55x55x96] CONV1: 96 11x11 filters at stride 4, pad 0
[27x27x96] MAX POOL1: 3x3 filters at stride 2
[27x27x96] NORM1: Normalization layer
[27x27x256] CONV2: 256 5x5 filters at stride 1, pad 2
[13x13x256] MAX POOL2: 3x3 filters at stride 2
[13x13x256] NORM2: Normalization layer
[13x13x384] CONV3: 384 3x3 filters at stride 1, pad 1
[13x13x384] CONV4: 384 3x3 filters at stride 1, pad 1
[13x13x256] CONV5: 256 3x3 filters at stride 1, pad 1
[6x6x256] MAX POOL3: 3x3 filters at stride 2
[4096] FC6: 4096 neurons
[4096] FC7: 4096 neurons
[1000] FC8: 1000 neurons (class scores)

AlexNet网络特点

• First use of ReLU；
• Used Norm layers (not common anymore)；
• Heavy data augmentation；
• Dropout 0.5；
• Batch size 128；
• SGD Momentum 0.9；
• Learning rate 1e-2, reduced by 10 manually when val accuracy plateaus；
• L2 weight decay 5e-4（正则化的权重衰减）；
• 7 CNN ensemble: 18.2% -> 15.4%（模型集成，取平均）。

由于当时所使用GPU的显存不够存放这么多参数，因此从第一个卷积层开始将参数分为两组，在两个GPU中训练，如第一个卷积层中参数被分为两组，每组有$11\times 11\times 3\times 48$个参数。

ZFNet

ZFNet网络结构图如下图所示：

ZFNet网络特点

• ZFNet框架大体与AlexNet一致；
• CONV1：Change from ($11\times 11$ stride 4) to ($7\times 7$ stride 2)；
• CONV3,4,5：Use 384,384,256 filters, instead of 512,1024,512 filters.

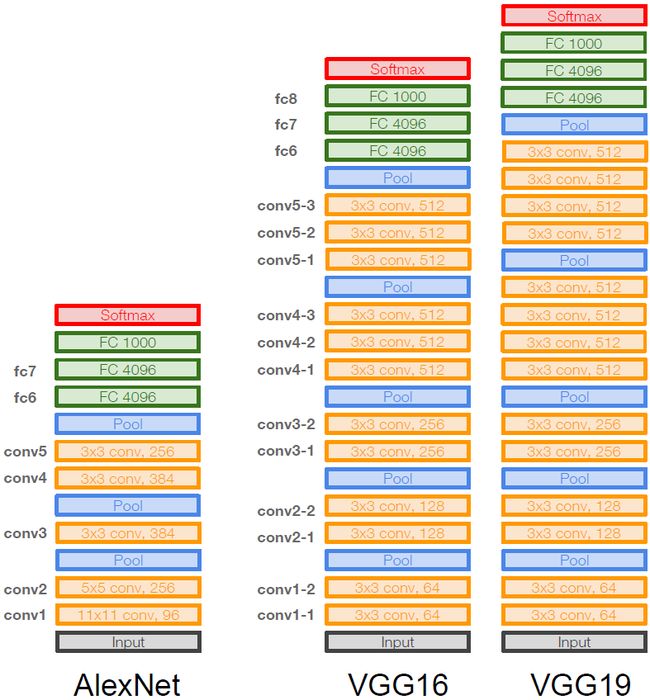
VGGNet

VGGNet网络结构图如下图所示：

VGG16网络详细信息如下

INPUT: [224x224x3] memory: 224x224x3=150K params: 0
CONV3-64: [224x224x64] memory: 224x224x64=3.2M params: (3x3x3)x64 = 1,728
CONV3-64: [224x224x64] memory: 224x224x64=3.2M params: (3x3x64)x64 = 36,864
POOL2: [112x112x64] memory: 112x112x64=800K params: 0
CONV3-128: [112x112x128] memory: 112x112x128=1.6M params: (3x3x64)x128 = 73,728
CONV3-128: [112x112x128] memory: 112x112x128=1.6M params: (3x3x128)x128 = 147,456
POOL2: [56x56x128] memory: 56x56x128=400K params: 0
CONV3-256: [56x56x256] memory: 56x56x256=800K params: (3x3x128)x256 = 294,912
CONV3-256: [56x56x256] memory: 56x56x256=800K params: (3x3x256)x256 = 589,824
CONV3-256: [56x56x256] memory: 56x56x256=800K params: (3x3x256)x256 = 589,824
POOL2: [28x28x256] memory: 28x28x256=200K params: 0
CONV3-512: [28x28x512] memory: 28x28x512=400K params: (3x3x256)x512 = 1,179,648
CONV3-512: [28x28x512] memory: 28x28x512=400K params: (3x3x512)x512 = 2,359,296
CONV3-512: [28x28x512] memory: 28x28x512=400K params: (3x3x512)x512 = 2,359,296
POOL2: [14x14x512] memory: 14x14x512=100K params: 0
CONV3-512: [14x14x512] memory: 14x14x512=100K params: (3x3x512)x512 = 2,359,296
CONV3-512: [14x14x512] memory: 14x14x512=100K params: (3x3x512)x512 = 2,359,296
CONV3-512: [14x14x512] memory: 14x14x512=100K params: (3x3x512)x512 = 2,359,296
POOL2: [7x7x512] memory: 7x7x512=25K params: 0
FC: [1x1x4096] memory: 4096 params: 7x7x512x4096 = 102,760,448
FC: [1x1x4096] memory: 4096 params: 4096x4096 = 16,777,216
FC: [1x1x1000] memory: 1000 params: 4096x1000 = 4,096,000

VGGNet网络特点

• 更小的filters，更深的网络；
• Only 3x3 CONV stride 1, pad 1 and 2x2 MAX POOL stride 2；
• 倒数第二层FC（FC7，1000个，即类别层之前）的hidden number=4096被验证已经能够很好地进行特征表达，可以用于在其他数据中提取特征，并有比较好的泛化性能；
• 作者先训练了一个11层的网络，使其收敛，之后将其扩展到16/19层，以此来解决深层网络收敛困难的问题（Batch Normalization提出后就不需要这种操作了）；
• 为何使用小的filters（3x3 CONV）：3个3x3的卷积层和1个7x7的卷积层拥有同样有效的感受野（解析可见https://blog.csdn.net/program_developer/article/details/80958716），但是其更深，更非线性化，且其参数数量更少，单层参数数量分别为3x（3x3xCxC）<7x7xCxC（C为channel数量）.

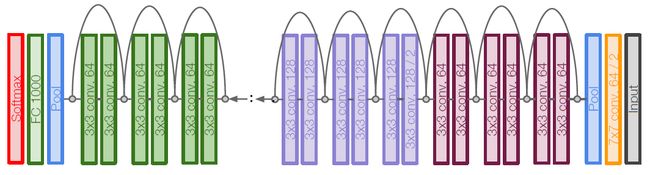
GoogleNet

GoogleNet网络结构图如下图所示：

GoogleNet网络特点

• 22层网络；
• 没有FC层；
• 为提高计算效率引入了“inception” module和“bottleneck”的概念；
• 网络有两个辅助输出（Auxiliary classification outputs）用于向低层的网络注入额外的梯度，以此解决网络收敛困难的问题（Batch Normalization提出后就不需要这种操作了）；
• 仅有5million个参数，比AlexNet少12倍。

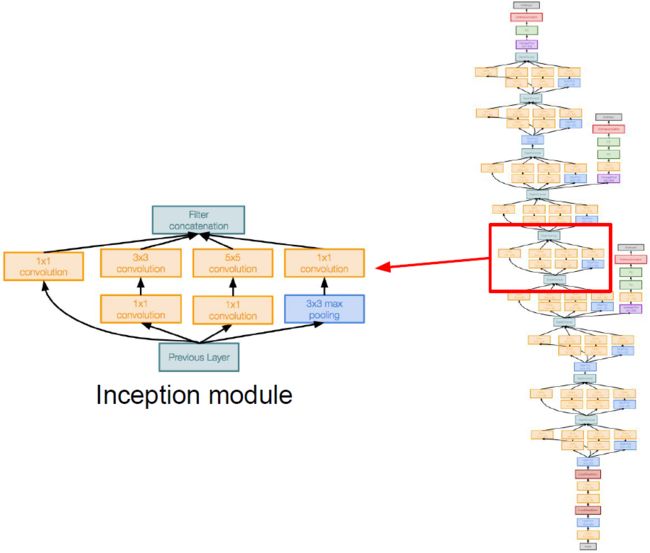
“inception” module

可以将网络看成是由局部网络拓扑（“inception” module）堆叠而成。对进入相同层的相同输入并行应用不同类别的滤波操作。我们将来自前面层的输入进行不同的卷积操作、池化操作，从而得到不同的输出，最后需要将所有输出在深度层面上连接到一起。计算与串联方式如下图所示：

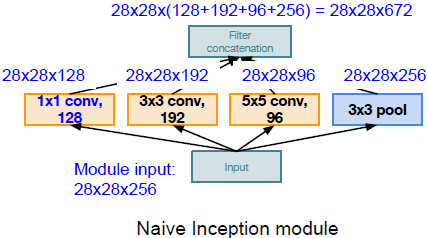
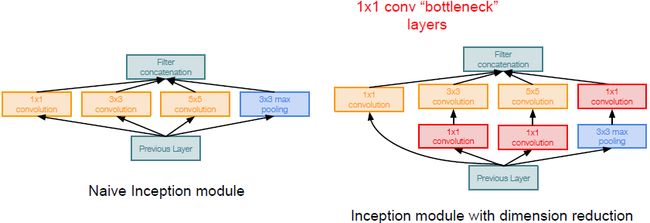
“blottleneck”

使用 “inception” module 后随之而来的问题就是：

• 单层的参数就达到854M个，计算量极大；
• 且数据经过每一个 “inception” module 后深度都会增加（光池化层得到输出数据的尺寸就已经与原数据相同）。

为解决上述问题，构建了称之为“bottleneck”的1x1卷积层以减少特征深度（如下图所示）：

改进后的“inception” module如下图所示：

Auxiliary classification outputs

GoogleNet同时拥有两个辅助输出，可以对前面几个层进行更多的梯度训练。当网络深度很深的时候，一些梯度信号会最小化并且丢失了前面几层的梯度信号，该方法能在一定层度上解决梯度消失的问题。

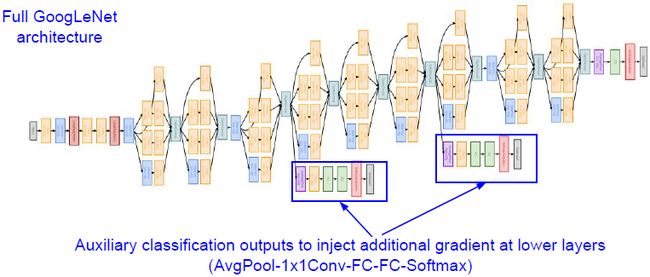
ResNet

ResNet网络结构图如下图所示：

ResNet网络特点：

• 152层；
• 利用残差层实现优化；
• 网络由残差盒堆叠而成（每一个残差盒包含两个3x3 CONV）；
• 如果将残差盒中的所有权重置零，那么残差盒的输出与输入就是相等的，因此，在某种层度上，这个模型是相对容易去训练的，并不需要添加额外的层；
• 神经网络中添加L2正则化的作用是迫使网络中的所有参数趋近于0，其他网络结构（如CONV）参数趋于0不太说得通。但在残差网络中，如果所有参数趋于0，那就是促使模型不再使用他不需要的层，因为它只趋使残差盒趋向同一性，也就不需要进行分类；
• 残差连接在反向传播时，为梯度提供了一个超级“高速通道”（梯度经过残差盒的加法门分流然后汇总），这使得网络训练更加容易（DenseNet和FractalNet也有类似的梯度直传式的连接）；
• 周期性的，会使用两倍数量的filters，用stride 2 CONV进行下采样（所有维度/2）；
• 网络起始处有一个额外的CONV；
• 没有额外的FC；
• 只有一个全局的AVE POOL；
• 每一个CONV后都带有一个BN；
• 用一个额外的带尺度因子的Xavier/2去初始化；
• 初始学习率为0.1，当Validation error停滞时，将其缩小十倍；
• Mini-batch size = 256；
• Weight decay = 1e-5.

残差盒（Residual block）

当我们在普通神经网络上堆叠越来越多的层时到底会发生什么？

由上图实验结果可知，56层网络的训练误差和测试误差都高于20层的网络。但是为何56层本应发生过拟合的NN的训练误差不如20层的NN呢，它最差也应该和20层的NN性能一样才对？

本文作者假设：这是一个优化问题，层深的模型更难优化。于是，作者提出了残差网络的概念，其与常规网络的区别如下图所示：

Residual block使这些网络层拟合的是残差映射H(x)-x而不是直接映射H(x)。某种意义上可以看成是一种对输入的修正。学习残差映射你只需知道什么是∆x=H(x)-x，通常来说，很多网络层之间实际上都是相差无几的，通过学习一个恒等映射加上很小的∆x（若恒等映射是最好的，只需将∆x置零），这样更容易学习。

与GoogleNet类似，如果网络层数较多的话，ResNet的残差盒会使用“bottleneck”来加速计算（如下图所示）。

扩展

Network in Network（NiN）

每个卷积层中都有一个完全连接的MLP(micronetwork)，以计算局部图像块的更多抽象特征。这个模型是GoogleNet和ResNet模型“bottleneck”的灵感来源。

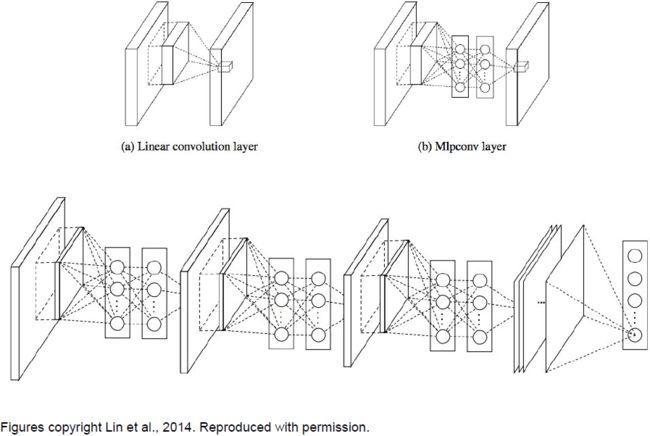
Identity Mappings in Deep Residual Networks

在ResNet的基础上进行修改，新的结构能够实现一种更直接的路径用于在整个网络中传播信息（将激活层移动到残差映射路径中）。

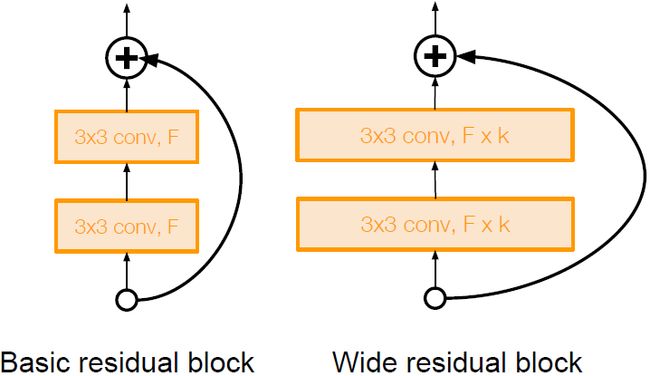
Wide Residual Networks

作者认为残差量是一个十分重要的因素而不是深度。使用了更宽的残差模块（FxK filters而不是F filters in each layer），宽网络的另一个优点是便于使用并行计算。本文旨在比较网络的宽度、深度和残差连接所做出的的贡献。

ResNeXt

通过多条平行路径增加残差盒宽度，这些分支总和被称为“cardinality”，思想类似于“inception”module。

Deep Networks with Stochastic Depth

动机是在训练过程中通过短网络减少消失梯度和训练时间。该思想类似于Dropout，只不过这里是沿网络深度方向的dropout。方法是在每次训练中随机drop某层子集（即ResNet中∆x=0，该层为恒等映射），在测试时使用完整的训练好的网络。

FractalNet

作者认为引入残差可能不是必须的，关键在于有效地从浅层网络转型为深层网络。因此他使用了上图所示这种分型结构，各层都以分形的形式存在，因此同时存在浅层和深层路径到大输出值。他们通过抛弃子路径的方式训练，类似于dropout，测试时使用整个分形网络。

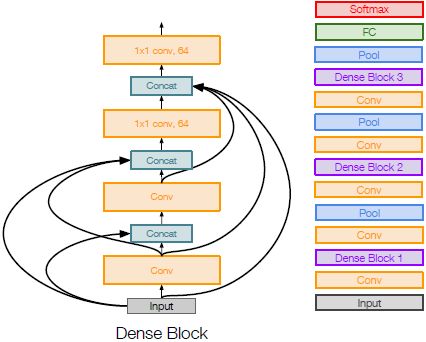
DenseNet

密集连接卷积神经网络。每个Dense block中每层都与其后的所有层以前馈的形式连接，因此在这个Dense block内，你对其的输入也是对所有其他各层的输入，你会计算每一个卷积输出，这些输出与其后的所有层连接，所有这些值集中起来，共同作为卷积层的输入。这一方法能缓解梯度消失的问题，加强特征图的传递，鼓励特征重用。

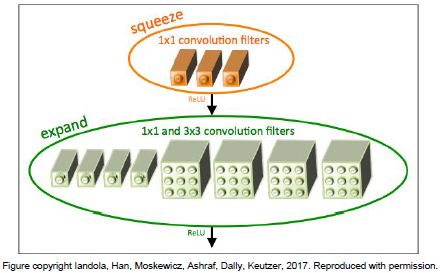
SqueezeNet

由一个个fire模块组成，每个fire模块都含有一个squeeze层，其由许多1x1的filters组成。接着，它再传递给一个扩大层含有一些1x1和3x3的filters。参数只有AlexNet的1/50，性能相似。

---

本博客与https://xuyunkun.com同步更新