2020全国大学生数学建模竞赛穿越沙漠第二问求解方法
第二问的模型相比第一问的区别就是天气未知,在天气未知的情况下,决定行动策略。因为天气未知,所以最优的决策不一定能得到最好的结果,因此就需要在第二问未知的条件下设计决策说明自己方法的优越性,一次穿越的结果优劣不能代表决策的最优。
在做比赛的之前看过知网研学的数模讲座,受到了胡旭东老师的启发。
胡老师讲了例子都非常有趣。(例子在五十分钟到六十分钟左右)
网址链接放在这里:https://k.cnki.net/CInfo/Index/6527
他有提到一个租买溜冰鞋的例子:
胡老师给出了滑冰者的租买策略,并且证明了它是最优的在线策略。

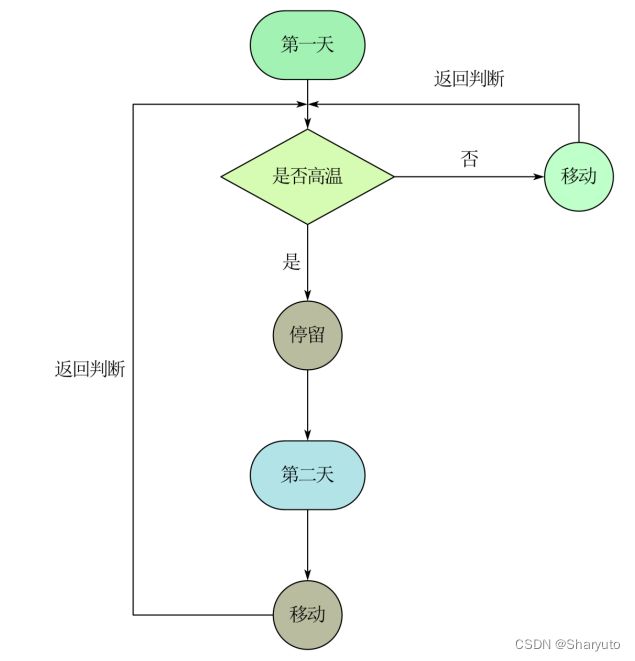
上面的滑冰者就好比这里的玩家,不知道之后会发生什么,但是知道第一天出现高温选择停留是比较划算的。如果到第二天还是出现了高温,那么第二天选择移动是最优策略。(就好比上面的T-1天租划算,第T天选择买是一个道理)。
对于沙漠穿越问题我们只知道历史天气状况和当前天气状况,通过这些已知数据去设计一种在线算法进行穿越沙漠的行动决策。
根据胡老师的结论,那就也可以得出这是玩家在未知天气情况下的最优移动策略。
那么总和的来说,玩家在地图3的策略就是晴朗必走,第一天若高温停留,第二天移动。
剩余的问题就是确定初始购买物资数量,通过对第一问的已知条件建立马尔可夫转移矩阵(假设游戏所有地图都在一个沙漠进行),模拟10天天气,代入修改好的模型。用lingo求解出需要的物资数量,模拟十次取平均值再加上一定的裕量,就是玩家出发时合理的购买物资数。
地图三求解完毕。
地图四要考虑挖矿和村落补给了,我把挖矿村落和移动分开进行了处理:
不在矿山的时候,还是那个移动模型,晴朗移动,第一天高温/沙暴停留,第二天移动(除非沙暴)。
其他还是由Lingo决定,是否去村落补给,是否去矿山挖矿,初始购买多少物资。
这种方法可以有效解决决策上的问题,但对于补给和初试物资的选取必须依据模拟结果给出的区间值去选取,物资选少了有概率穿越不了沙漠,但其实这也是天气未知情况下的通病。同时对于挖矿的决策(地图四),本文是估计了挖矿的收益期望值是在[550 835],这意味无论什么天气,挖矿的收益一定大于消耗值。因此到了矿场后应全部选择挖矿,直到所剩天数等于路程数的时候选择返回。(考虑沙暴情况的话多预留2-3天)大致内容就是这样:
这些用lingo的if语言很容易表达,只不过容易变为非线性约束,转化成线性约束可能需要费点功夫。不过地图三和地图四的模型规模并不是很大,lingo也能很快的得到结果。其实也就是在前面一二问的基础上加上这两个约束:
![]()
发现可以改成线性约束:
![]()
最后代码附在这里:(天气是模拟出来的,代码可能和上面说的方法有些出入。。挖矿决策还是由lingo自行决定的 看一下就好了)
sets:
a1/1..25/;
a2(a1,a1):d;
a3/1..30/:n,cX,cY,yY,yX,w,z1,z2,z3,b,r,aX,aY,kk,wuzi,shui;
a4(a3,a1,a1):x;
a5(a3,a1);
endsets
x1>0;
y1>0;
@gin(x1);
@gin(y1);
@for(a3(i):@bin(z1(i)));
@for(a3(i):@bin(z2(i)));
@for(a3(i):@bin(z3(i)));
@for(a3(i):@gin(cX(i)));
@for(a3(i):@gin(cY(i)));
@for(a3(i):cX(i)>=0);
@for(a3(i):cY(i)>=0);
!各变量约束;
weight=3*x1+2*y1;
cost=5*x1+10*y1;
cost<=10000;
weight<=1200;
!初始约束;
@for(a4(i,j,k):x(i,j,k)<=d(j,k));
!只走接壤;
@for(a4(i,j,k):@bin(x(i,j,k)));
!整数规划;
@for(a3(i):@sum(a2(j,k):x(i,j,k))=1);
!每天一决策;
@sum(a1(k):x(1,1,k))=1;
!起点出发;
@sum(a5(i,j)|j#ne#25:x(i,j,25))=1;
!有一天走去终点;
@for(a3(i)|i#lt#30:x(i+1,25,25)=@sum(a1(j):x(i,j,25)));
!到达终点停止;
@for(a5(i,j)|i#lt#30:@sum(a1(k):x(i+1,j,k))=@sum(a1(k):x(i,k,j)));
!当天出发=前一天目的地;
@for(a3(i):z1(i)=@sum(a1(j):x(i,j,j)));
!是否停留;
@for(a3(i):w(i)-@sum(a1(j):x(i,j,j))<=2);
!沙暴必须停留;
@for(a3(i):cX(i)<=1000*z3(i));
!购买物资条件;
@for(a3(i):cY(i)<=1000*z3(i));
!购买水条件;
@for(a3(i):r(i)=1000*z2(i));
!挖矿条件;
@for(a3(i):10*cX(i)+20*cY(i)-r(i)<=10000-cost-@sum(a3(j)|j#lt#i:10*cX(j)+20*cY(j)-r(j)));
!资金限制;
@for(a3(i):3*cX(i)+2*cY(i)-3*yX(i)-2*yY(i)<=1200-weight-@sum(a3(j)|j#lt#i:3*cX(j)+2*cY(j)-3*yX(j)-2*yY(j)));
!重量限制;
@for(a3(i):yX(i)=aX(i)*b(i));
@for(a3(i):yY(i)=aY(i)*b(i));
!消耗量函数;
@for(a3(i):aX(i)=@if(w(i)#eq#1,5,@if(w(i)#eq#2,8,10)));
@for(a3(i):aY(i)=@if(w(i)#eq#1,7,@if(w(i)#eq#2,6,10)));
@for(a3(i):b(i)=2+2*z2(i)-z1(i)-x(i,25,25));
!消耗量关于天气 决策的函数关系;
eX=x1-@sum(a3(i):yX(i)-cX(i));
eY=y1-@sum(a3(i):yY(i)-cY(i));
@for(a3(i):z2(i)<=x(i,18,18));
@for(a3(i):z3(i)<=@sum(a1(j):x(i,j,14)+x(i,14,j)));
!挖矿 购买 决策约束条件;
max=10000-cost-@sum(a3(i):10*cX(i)+20*cY(i)-r(i))+2.5*eX+5*eY;
!目标函数;
!@for(a3(i)|i#lt#30:z1(i+1)=@if(x(i,25,25)#eq#1,1,@if(w(i+1)#eq#3,1,@if(x(i+1,18,18)#ne#1,@if(z1(i)#eq#1,0,z1(i+1)),z1(i+1)))));
!@for(a3(i):z1(i)=@if(x(i,25,25)#eq#1,1,@if(x(i,18,18)#ne#1,@if(w(i)#eq#1,0,z1(i)),1)));
@for(a3(i)|i#lt#30:z1(i)+w(i+1)+1000*@sum(a1(j):x(i,j,18))>=2*(z1(i+1)-x(i,25,25)));
@for(a3(i):kk(i)=10000-cost-@sum(a3(j)|j#lt#i:10*cX(j)+20*cY(j)-r(j)));
@for(a3(i):shui(i)=x1-@sum(a3(j)|j#lt#i:yX(j)-cX(j))-yX(i));
@for(a3(i):wuzi(i)=y1-@sum(a3(j)|j#lt#i:yY(j)-cY(j))-yY(i));
@for(a3(i):wuzi(i)>=0);
@for(a3(i):shui(i)>=0);
data:
@text('data.txt')=@write('最大资金数为',kk(30)+2.5*shui(30)+5*wuzi(30),'元 行走路径为:',@newline(1));
@text('data.txt')=@writefor(a4(i,j,k)|x(i,j,k)#eq#1 #and# x(i,25,25)#eq#0:'第',i,'天','从',j,'点去往',k,'点,','消耗水',yX(i),'个,食物',yY(i),'个,剩余水',shui(i),'个,食物有',wuzi(i),'个;',@newline(1));
@text('data.txt')=@writefor(a3(i)|@sum(a1(j):x(i,j,25))#eq#1 #and# x(i,25,25)#eq# 0:'在第',i,'天抵达终点。',@newline(1));
@text('data.txt')=@writefor(a3(i)|z2(i)#eq#1:'在第',i,'天选择挖矿',@newline(1));
@text('data.txt')=@writefor(a3(i)|z3(i)#eq#1:'在第',i,'天从村落里购买了',cX,'个食物和',cY,'个水',@newline(1));
w=2 3 2 2 2 3 2 1 1 2 2 2 1 2 3 2 2 2 2 2 1 2 2 2 2 1 2 2 2 1;
d=1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 1 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 1 0 0 0 1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 1 0 0 0 1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 1 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 1 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 1 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 1 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 1 1 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1;
enddata