数学建模:线性规划—投资的收益和风险模型 (Python 求解)
目录
-
- 模型建立
- 模型 I : 固定风险水平, 优化收益
- 模型 II : 固定盈利水平, 极小化风险
- 模型 III : 两个目标函数加权求和
市场上有 n n n 种资产 s i {s_i} si ( i = 1 , 2 , ⋯ , n i = 1,2, \cdots ,n i=1,2,⋯,n )可以选择,现用数额为 M M M 的充分大的资金作一个时期的投资。这 n n n 种资产在这一时期内购买 s i {s_i} si 的平均收益率为 r i {r_i} ri ,风险损失率为 q i {q_i} qi ,投资越分散,总的风险越少,总体风险可用投资的 s i {s_i} si 中最大的一个风险来度量。
购买 s i {s_i} si 时要付交易费,费率为 p i {p_i} pi ,当购买额不超过给定值 u i {u_i} ui 时,交易费按购买 u i {u_i} ui 计算。另外,假定同期银行存款利率是 r 0 {r_0} r0 ,既无交易费又无风险( r 0 = 5 % {r_0} = 5\% r0=5% )。
给该公司设计一种投资组合方案,即用给定资金 ,有选择地购买若干种资产或存银行生息,使净收益尽可能大,使总体风险尽可能小。
已知 n = 4 n = 4 n=4, 相关数据如下表.
| s i {s_i} si | r i {r_i} ri (%) | q i {q_i} qi (%) | p i {p_i} pi (%) | u i {u_i} ui (元) |
|---|---|---|---|---|
| s 1 {s_1} s1 | 28 | 2.5 | 1 | 103 |
| s 2 {s_2} s2 | 21 | 1.5 | 2 | 198 |
| s 3 {s_3} s3 | 23 | 5.5 | 4.5 | 52 |
| s 4 {s_4} s4 | 25 | 2.6 | 6.5 | 40 |
模型建立
设 x i x_i xi 表示投资项目 s i s_i si 的资金, a a a 表示投资风险度, Q Q Q 表示总体收益, 建立如下多目标线性规划模型
{ max ∑ i = 0 n ( r i − p i ) x i min max 1 ≤ i ≤ n { q i x i } s . t . { ∑ i = 0 n ( 1 + p i ) x i = M x i ≥ 0 , i = 0 , 1 , ⋯ , n \begin{gathered} \left\{\begin{array}{l} \max \quad \sum_{i=0}^{n}\left(r_{i}-p_{i}\right) x_{i} \\ \min \quad \max _{1 \leq i \leq n}\left\{q_{i} x_{i}\right\} \end{array}\right. \\ s.t. \left\{\begin{array}{l} \sum_{i=0}^{n}\left(1+p_{i}\right) x_{i}=M \\ x_{i} \geq 0, \quad i=0,1, \cdots, n \end{array}\right. \end{gathered} {max∑i=0n(ri−pi)ximinmax1≤i≤n{qixi}s.t.{∑i=0n(1+pi)xi=Mxi≥0,i=0,1,⋯,n
在实际投资中, 投资者承受风险的程度不一样, 下面分别通过给定风险界限, 总收益下限和对风险, 收益分别赋予权重建立三个简化模型把多目标线性规划变成单目标线性规划求解.
模型 I : 固定风险水平, 优化收益
给定风险一个界限 a a a ,使最大的一个风险 q i x i M ⩽ a \displaystyle{\frac{{{q_i}{x_i}}}{M} \leqslant a} Mqixi⩽a ,可找到相应的投资方案,把多目标规划变成单目标线性规划
max ∑ i = 0 n ( r i − p i ) x i s.t. { q i x i M ≤ a , i = 1 , 2 , ⋯ , n , ∑ i = 0 n ( 1 + p i ) x i = M , x i ≥ 0 , i = 0 , 1 , ⋯ , n . \begin{gathered} \max \quad \sum_{i=0}^{n}\left(r_{i}-p_{i}\right) x_{i} \\ \text { s.t. }\left\{\begin{array}{l} \frac{q_{i} x_{i}}{M} \leq a, i=1,2, \cdots, n, \\ \sum_{i=0}^{n}\left(1+p_{i}\right) x_{i}=M, \quad x_{i} \geq 0, \quad i=0,1, \cdots, n . \end{array}\right. \end{gathered} maxi=0∑n(ri−pi)xi s.t. {Mqixi≤a,i=1,2,⋯,n,∑i=0n(1+pi)xi=M,xi≥0,i=0,1,⋯,n.
设 M = 1 M=1 M=1, 代入数据
min f = ( − 0.05 , − 0.27 , − 0.19 , − 0.185 , − 0.185 ) ⋅ ( x 0 , x 1 , x 2 , x 3 , x 4 ) T s . t . { 0.025 x 1 ≤ a 0.015 x 2 ≤ a 0.055 x 3 ≤ a 0.026 x 4 ≤ a x 0 + 1.01 x 1 + 1.02 x 2 + 1.045 x 3 + 1.065 x 4 = 1 x i ≥ 0 ( i = 0 , 1 , ⋯ , 4 ) \begin{gathered} { \min } \quad f=(-0.05,-0.27,-0.19,-0.185,-0.185) \cdot\left(x_{0}, x_{1}, x_{2}, x_{3}, x_{4}\right)^{T} \\ { s.t. }\left\{\begin{array}{l} 0.025 x_{1} \leq a \\ 0.015 x_{2} \leq a \\ 0.055 x_{3} \leq a \\ 0.026 x_{4} \leq a \\ x_{0}+1.01 x_{1}+1.02 x_{2}+1.045 x_{3}+1.065 x_{4}=1 \\ x_{i} \geq 0(i=0,1, \cdots, 4) \end{array}\right. \end{gathered} minf=(−0.05,−0.27,−0.19,−0.185,−0.185)⋅(x0,x1,x2,x3,x4)Ts.t.⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧0.025x1≤a0.015x2≤a0.055x3≤a0.026x4≤ax0+1.01x1+1.02x2+1.045x3+1.065x4=1xi≥0(i=0,1,⋯,4)
从 a = 0 a=0 a=0 开始, 以步长 Δ a = 0.001 \Delta a=0.001 Δa=0.001 进行循环搜索, 使用 scipy.optimize.linprog 求解
import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import linprog
c = [-0.05,-0.27,-0.19,-0.185,-0.185]
A = np.c_[np.zeros(4),np.diag([0.025,0.015,0.055,0.026])]
# np.r_ : 按列连接两个矩阵,即把两矩阵上下相加,要求列数相等
# np.c_ : 按行连接两个矩阵,即把两矩阵左右相加,要求行数相等
Aeq =[[1,1.01,1.02,1.045,1.065]]; beq = [1]
a=0; aa=[]; rr=[]
while a<0.05:
b = np.ones(4)*a
res = linprog(c,A,b,Aeq,beq)
x = res.x; Q = -res.fun
aa.append(a); rr.append(Q) #保存最优值
a = a+0.001
plt.rc('font',size=16); plt.rc('font',family='SimHei'); plt.rc('text',usetex=False)
plt.plot(aa,rr,'k')
plt.plot(aa,rr,'r.')
plt.xlabel("风险 a"); plt.ylabel("收益 R",rotation=0)
plt.show()
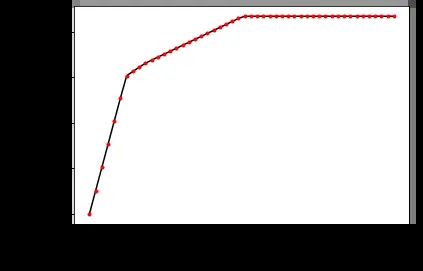
从图中可以看出, 风险越大, 收益越大, 在 a = 0.006 a=0.006 a=0.006 附近有一个转折点, 在这一点左边, 风险增加很少时, 利润增长很快; 在这一点右边, 风险增加很大时, 利润增长很缓慢, 所以对于风险和收益没有特殊偏好的投资者来说,应该选择曲线的转折点作为最优投资组合, 大约是 a = 0.006 a=0.006 a=0.006, Q = 0.2019 Q=0.2019 Q=0.2019.
模型 II : 固定盈利水平, 极小化风险
总盈利至少达到水平 k k k 以上,在风险最小的情况下寻求相应的投资组合, 建立模型
min max 1 ≤ i ≤ n { q i x i } s . t . { ∑ i = 0 n ( r i − p i ) x i ≥ k ∑ i = 0 n ( 1 + p i ) x i = M , x i ≥ 0 , i = 0 , 1 , ⋯ , n . \begin{gathered} \min \quad \max _{1 \leq i \leq n}\left\{q_{i} x_{i}\right\} \\ { s.t. }\left\{\begin{array}{l} \sum_{i=0}^{n}\left(r_{i}-p_{i}\right) x_{i} \geq k \\ \sum_{i=0}^{n}\left(1+p_{i}\right) x_{i}=M, \\ x_{i} \geq 0, \quad i=0,1, \cdots, n . \end{array}\right. \end{gathered} min1≤i≤nmax{qixi}s.t.⎩⎨⎧∑i=0n(ri−pi)xi≥k∑i=0n(1+pi)xi=M,xi≥0,i=0,1,⋯,n.
设 x n + 1 = max 1 ≤ i ≤ n { q i x i } x_{n+1}=\max _{1 \leq i \leq n}\left\{q_{i} x_{i}\right\} xn+1=max1≤i≤n{qixi}, 则可以线性化为
min x n + 1 , s . t . { q i x i ≤ x n + 1 , i = 1 , 2 , ⋯ , n , ∑ i = 0 n ( r i − p i ) x i ≥ k ∑ i = 0 n ( 1 + p i ) x i = M , x i ≥ 0 , i = 0 , 1 , ⋯ , n \begin{gathered} &\min \quad x_{n+1}, \\ & { s.t. }\left\{\begin{array}{l} q_{i} x_{i} \leq x_{n+1}, \quad i=1,2, \cdots, n, \\ \sum_{i=0}^{n}\left(r_{i}-p_{i}\right) x_{i} \geq k \\ \sum_{i=0}^{n}\left(1+p_{i}\right) x_{i}=M, \\ x_{i} \geq 0, \quad i=0,1, \cdots, n \end{array}\right. \end{gathered} minxn+1,s.t.⎩⎪⎪⎨⎪⎪⎧qixi≤xn+1,i=1,2,⋯,n,∑i=0n(ri−pi)xi≥k∑i=0n(1+pi)xi=M,xi≥0,i=0,1,⋯,n
即
min x 5 , s . t . { 0.025 x 1 − x 5 ≤ 0 0.015 x 2 − x 5 ≤ 0 0.055 x 3 − x 5 ≤ 0 0.026 x 4 − x 5 ≤ 0 − 0.05 x 0 − 0.27 x 1 − 0.19 x 2 − 0.185 x 3 − 0.185 x 4 ≤ − k , x 0 + 1.01 x 1 + 1.02 x 2 + 1.045 x 3 + 1.065 x 4 = 1 x i ≥ 0 , i = 0 , 1 , ⋯ , 5. \begin{gathered} &\min \quad x_{5}, \\ & { s.t. }\left\{\begin{array}{l} 0.025 x_{1}-x_{5} \leq 0 \\ 0.015 x_{2}-x_{5} \leq 0 \\ 0.055 x_{3}-x_{5} \leq 0 \\ 0.026 x_{4}-x_{5} \leq 0 \\ -0.05 x_{0}-0.27 x_{1}-0.19 x_{2}-0.185 x_{3}-0.185 x_{4} \leq-k, \\ x_{0}+1.01 x_{1}+1.02 x_{2}+1.045 x_{3}+1.065 x_{4}=1 \\ x_{i} \geq 0, \quad i=0,1, \cdots, 5 . \end{array}\right. \end{gathered} minx5,s.t.⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧0.025x1−x5≤00.015x2−x5≤00.055x3−x5≤00.026x4−x5≤0−0.05x0−0.27x1−0.19x2−0.185x3−0.185x4≤−k,x0+1.01x1+1.02x2+1.045x3+1.065x4=1xi≥0,i=0,1,⋯,5.
k k k 从 0.05 0.05 0.05, 以 0.005 0.005 0.005 步长迭代, 用 cvxpy 求解
import matplotlib.pyplot as plt
import numpy as np
import cvxpy as cp
x=cp.Variable(6,pos=True)
obj=cp.Minimize(x[5])
a1=np.array([0.025, 0.015, 0.055, 0.026])
a2=np.array([0.05, 0.27, 0.19, 0.185, 0.185])
a3=np.array([1, 1.01, 1.02, 1.045, 1.065])
k=0.05; kk=[]; qq=[]
while k<0.27:
con=[cp.multiply(a1,x[1:5])-x[5]<=0,a2@x[:-1]>=k, a3@x[:-1]==1]
prob=cp.Problem(obj,con)
prob.solve(solver='GLPK_MI')
kk.append(k); qq.append(prob.value)
k=k+0.005
plt.rc('text',usetex=False); plt.rc('font',size=16); plt.rc('font',family='SimHei')
plt.plot(kk,qq,'k')
plt.plot(kk,qq,'b.')
plt.xlabel("收益 k"); plt.ylabel("风险 Q",rotation=0)
plt.show()

从图中可以看出, 风险越大, 收益越大, 拐点在 k = 0.21 , Q = 0.0077 k=0.21, Q=0.0077 k=0.21,Q=0.0077 附近.
模型 III : 两个目标函数加权求和
对风险、收益分别赋予权重 s ( 0 < s ≤ 1 ) s(0s(0<s≤1) 和 ( 1 − s ) (1-s) (1−s), 建立模型
min s ( max 1 ⩽ i ⩽ n { q i x i } ) − ( 1 − s ) ∑ i = 0 n ( r i − p i ) x i , s . t . { ∑ i = 0 n ( 1 + p i ) x i = M , x i ⩾ 0 , i = 0 , 1 , 2 , ⋯ , n \begin{gathered} \min \;s\left( \mathop {\max }\limits_{1 \leqslant i \leqslant n} \,\{ {q_i}{x_i}\} \right) - (1 - s)\sum\limits_{i = 0}^n {({r_i} - {p_i}){x_i}} , \\ {{s}}{{.t}}{{.}}\left\{ \begin{gathered} \sum\limits_{i = 0}^n {(1 + {p_i}){x_i} = M,} \\ {x_i} \geqslant 0,\quad i = 0,1,2, \cdots ,n \\ \end{gathered} \right. \\ \end{gathered} mins(1⩽i⩽nmax{qixi})−(1−s)i=0∑n(ri−pi)xi,s.t.⎩⎪⎪⎨⎪⎪⎧i=0∑n(1+pi)xi=M,xi⩾0,i=0,1,2,⋯,n
令 x n + 1 = max 1 ≤ i ≤ n { q i x i } x_{n+1}=\max _{1 \leq i \leq n}\left\{q_{i} x_{i}\right\} xn+1=max1≤i≤n{qixi}, 线性化为
min w x n + 1 − ( 1 − w ) ∑ i = 0 n ( r i − p i ) x i \min \quad w x_{n+1}-(1-w) \sum_{i=0}^{n}\left(r_{i}-p_{i}\right) x_{i} minwxn+1−(1−w)i=0∑n(ri−pi)xi
s.t. { q i x i ⩽ x n + 1 , i = 1 , 2 , ⋯ , n ∑ i = 0 n ( 1 + p i ) x i = M , x i ⩾ 0 , i = 0 , 1 , 2 , ⋯ , n . \text { s.t. }\left\{\begin{array}{ll} q_{i} x_{i} \leqslant x_{n+1}, & i=1,2, \cdots, n \\ \sum_{i=0}^{n}\left(1+p_{i}\right) x_{i}=M, & \\ x_{i} \geqslant 0, & i=0,1,2, \cdots, n . \end{array}\right. s.t. ⎩⎨⎧qixi⩽xn+1,∑i=0n(1+pi)xi=M,xi⩾0,i=1,2,⋯,ni=0,1,2,⋯,n.
import matplotlib.pyplot as plt
import numpy as np
import cvxpy as cp
x=cp.Variable(6,pos=True)
r=np.array([0.05, 0.28, 0.21, 0.23, 0.25]) #收益率
p=np.array([0, 0.01, 0.02, 0.045, 0.065]) #交易费率
q=np.array([0, 0.025, 0.015, 0.055, 0.026]) #风险损失率
con=[q[1:]@x[1:-1]<=x[5], (1+p)@x[:-1]==1, x>=0]
ss,qq,rr=[],[],[]
ww = set()
for w in range(1001):
obj=cp.Minimize((w/1000)*x[5]-(1-w/1000)*((r-p)@x[:-1]))
prob=cp.Problem(obj,con)
prob.solve(solver='GLPK_MI')
ss.append(prob.value)
qq.append(x.value[5]) #风险
rr.append((r-p)@x.value[:-1]) #收益
ww.add(((r-p)@x.value[:-1], x.value[5]))
plt.rc('font',size=16); plt.rc('font',family='SimHei'); plt.rc('text',usetex=False)
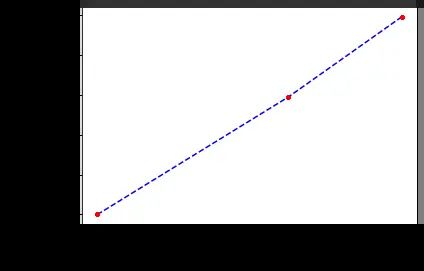
plt.plot(rr,qq,'b--')
plt.plot(rr,qq,'r.')
plt.xlabel("收益 R"); plt.ylabel("风险 Q",rotation=0)
plt.show()
投资的收益越大,风险也越大。投资者可以根据自己对风险喜好的不同,选择合适的投资方案,拐点在 R = 0.186 , Q = 0.015 R=0.186, Q=0.015 R=0.186,Q=0.015 左右.