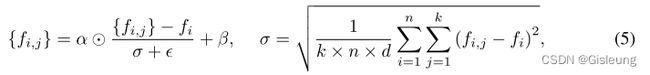【文献笔记】PointMLP
写在前面,笔者在阅读该篇文献时,发现当时网络上没有很好的该文献的阅读笔记
故生此拙笔之作。。。
ICLR 2022 ;Rethinking Network Design and Local Geometry in Point Cloud: A Simple Residual MLP Framework
论文地址:Rethinking Network Design and Local Geometry in Point Cloud: A Simple Residual MLP Framework (arxiv.org)
代码地址:PointMLP-Pytorch
文章目录
-
- 当前的现状
- 网络结构
- 简单回顾已有的网络
- 本文使用的 MLP
- 几何仿射模块
- 轻量版本 PointMLP-elite
- 实验分析
- 总结
通篇作者在向外传达:我的方法
PointMLP纯纯的清新脱俗,化繁为简
当前的现状
作者总结:
- 大家挤破头的在局部特征提取上做文章,导致提取器(local geometric extractors)越来越复杂,性能越来越拉跨(虽然精度有所提升)
- 对局部几何特征提取的研究工作,将近饱和。(意思目前的提取器已经能很好的提取特征了)
- 当前的3D point cloud applications(生产应用)中,更倾向于使用PointNet++等(简洁轻量),很少使用复杂的提取器
- 且作者认为点云的深度任务活在图像的阴影下。(意思是别人就会照搬抄袭隔壁图像的新方法,如transformer)
作者认为,
- 研究更为详细的局部几何信息可能不是点云分析的关键。要重新审视点云分析中的简洁设计理念。
- 本文的 PointMLP 遵循 PointNet++ 的设计理念,但探索了更简单但更深入的网络架构。
- 本文没有精心设计的局部几何提取操作,纯深度分层 MLP 架构也能够表现出令人满意的性能甚至更好的结果。
- 本文没有刻意追随视觉社区的趋势,而是追求一种本质上简单且经验强大的点云分析架构
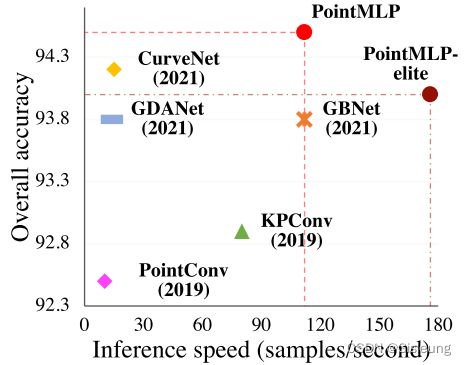
show 秀:
有一说一,确实在速度和精度上表现SOTA
网络结构
文章通过一个简单的前馈残差 MLP 网络(称为 PointMLP)来学习点云表示,该网络分层聚合 MLP 提取的局部特征,并放弃使用精细的局部几何提取器。
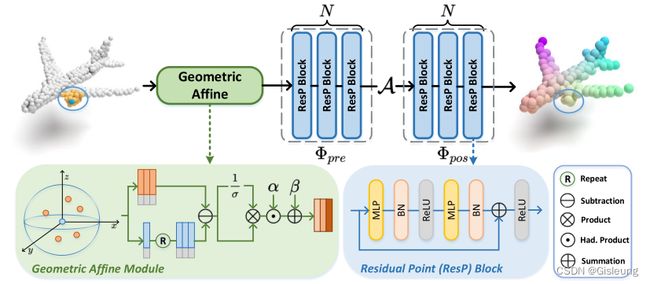
详细框架如下图所示:
图 :PointMLP 中一个阶段的概述。给定输入点云,PointMLP 使用残差点 MLP 块 Residual Point Block 逐步提取局部特征。在每个阶段,作者首先使用几何仿射模块 Geometric Affine Module 变换局部点,然后分别在聚合操作之前和之后提取它们(几何特征)。 PointMLP 通过重复多个阶段逐步扩大感受野并模拟完整的点云几何信息。
简单回顾已有的网络
作者简要介绍了三个代表性的网络结构(不做重点展开)
- PointNet++:作者认为最具开创性,其核算子可以表示为:
![]()
其中:A表示聚合过程(PointNet++中使用MaxPooling);$\Phi $ 表示特征计算过程(PointNet++中使用MLP);f_ij表示第i个采样点的第j个邻居点的特征
-
RSCNN …
-
Point Transformer …
本文使用的 MLP
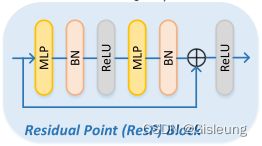
PointMLP的一个阶段(即ResP Block)可以用公式表示为:
![]()
式中:
- Φpre (·) 和 Φpos (·) 是残差点 MLP 块:共享的 Φpre (·) 旨在从局部区域学习共享权重,而 Φpos (·) 用于提取深度聚合特征。
其映射函数可以写成一系列同质的残差 MLP 块:MLP(x) + x,其中 MLP 由 FC、归一化和激活层组合而成(重复两次)。
- A(·) 特征聚合使用最大池化操作。
在分层和深度网络中,需要将上述阶段重复执行(堆叠) s 次。尽管 PointMLP 的框架很简洁,但是:
- 由于PointMLP只利用了MLPs,自然对置换具有不变性,完美契合了点云的特性
- 通过结合残差连接,PointMLP 可以很容易地扩展到几十层,从而产生深度特征表示
- 由于没有包含复杂的提取器并且主要操作只是高度优化的前馈 MLP,即使引入更多层,PointMLP 仍然可以有效地执行
在实验中,重复执行4次(s=4)阶段,使用KNN(k=24)查找领域点
几何仿射模块
geometric affine module
**该模块解决的问题:**由于点云的密度不均匀和几何结构不确定性,对于不同的局部区域,需要使用不同的提取器,用以提高性能(精度)
表示为:
式中:
- α ∈ Rd 和 β ∈ Rd 是可学习的参数
- ⊙表示
哈达玛积(Hadamard product) - $\varepsilon $ = 1e−5 是数值稳定性的一个小数
- σ 是一个标量,描述了所有本地组和通道的特征偏差
通过这样做,作者将局部点转换为正态分布,同时保持原始几何属性
轻量版本 PointMLP-elite
为进一步提高效率(速度更快,更轻量级),作者引入 elite 版本,大大提升了训练测试速度,降低了内存要求,虽然精度比PointMLP略微差一点,但也好过大多数
❓ 是如何是实现的?
- 将中间 FC 层的通道数减少 r 倍。该方法将残差MLP的参数从2d2减少至(2d2)/r,默认设置r = 4
- 略微调整了网络架构
- 减少MLP 块
- 减少嵌入维数
此外,作者还尝试了分组FC操作,但是实验发现并没有提高性能,就放弃了。
实验分析
- 在多个基准数据集上进行对比试验
- 物体分类实验表现不俗,达到SOTA,论文中列出了详细对比数据
- 部件分割文章中只给了效果图,没有详细列出对比数据,估计一般
- 语义分割文章压根没提
- 消融实验
- 网络深度(24、40、56层)
- 几何仿射模块
- 组件(Φpre、Φpos、Affine)
- Res.,残差块
该实验部分细节建议直接看文章中的原图。
总结
在本文中,作者提出了一种简单而强大的架构,名为 PointMLP,用于点云分析。 PointMLP 背后的关键见解是复杂的局部几何提取器可能对性能并不重要。
作者首先用简单的残差 MLP 表示局部点,因为它们是置换不变且简单的。然后作者引入了一个轻量级的几何仿射模块来提高性能。
为了进一步提高效率,作者还引入了一个轻量级网络 PointMLP-elite。
实验结果表明,PointMLP 在简单性和效率方面优于不同基准上的相关工作。
作者希望这个新颖的想法能够激发社区重新思考点云中的网络设计和局部几何。
>>> 完 <<<
其实笔者有很多文献笔记,鉴于网络上有更优秀的笔记(同一文献),就不制造网络垃圾了