Leetcode刷题笔记——动态规划
动态规划的⼀般流程就是三步:暴⼒的递归解法 -> 带备忘录的递归解法 -> 迭代的动态规划解法。
就思考流程来说,就分为⼀下⼏步:找到状态和选择 -> 明确 dp 数组/函数的定义 -> 寻找状态之间的关系。
- 明确dp[i][j]表示的是什么意思
- 找到状态转移方程
- 确定初始边界
注意:dp是自下往上的方法,故明确base case或者说边界条件后,根据动态转移方程从dp[0] => dp[1] => dp[2] => ... => dp[n]
509. Fibonacci Number
The Fibonacci numbers, commonly denoted F(n) form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1. That is,
F(0) = 0, F(1) = 1
F(n) = F(n - 1) + F(n - 2), for n > 1.
Given n, calculate F(n).
Example 1:
Input: n = 2
Output: 1
Explanation: F(2) = F(1) + F(0) = 1 + 0 = 1.
Example 2:
Input: n = 3
Output: 2
Explanation: F(3) = F(2) + F(1) = 1 + 1 = 2.
Example 3:
Input: n = 4
Output: 3
Explanation: F(4) = F(3) + F(2) = 2 + 1 = 3.
Constraints:
0 <= n <= 30
我的解法:暴力递归
class Solution {
public:
int fib(int n) {
if (n<=1) return n;
else return fib(n-1) + fib(n-2);
}
};
复杂度:递归算法的时间复杂度怎么计算?子问题个数乘以解决一个子问题需要的时间。
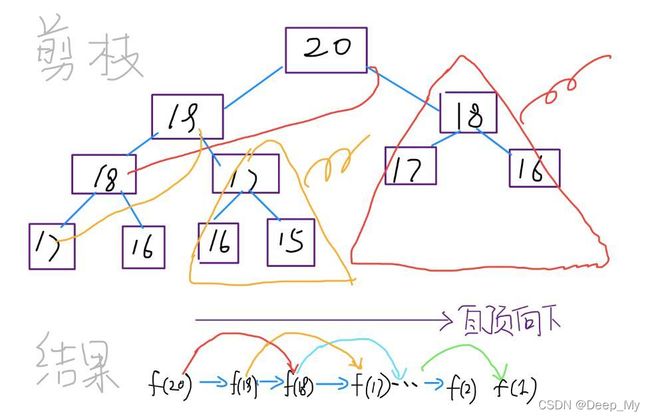
子问题个数,即递归树中节点的总数。显然二叉树节点总数为指数级别,所以子问题个数为 O(2^n)。
解决一个子问题的时间,在本算法中,没有循环,只有 f(n - 1) + f(n - 2) 一个加法操作,时间为 O(1)。
所以,这个算法的时间复杂度为 O(2^n),指数级别,爆炸。
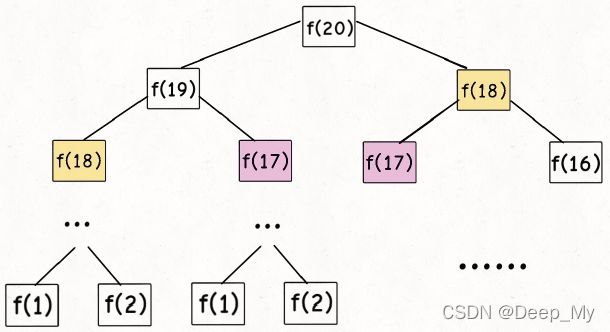
观察递归树,很明显发现了算法低效的原因:存在大量重复计算,比如 f(18) 被计算了两次,而且你可以看到,以 f(18) 为根的这个递归树体量巨大,多算一遍,会耗费巨大的时间。更何况,还不止 f(18) 这一个节点被重复计算,所以这个算法及其低效。
动态规划问题的第一个性质:重叠子问题。
第二步,解决方案:带备忘录的递归解法
即然耗时的原因是重复计算,那么我们可以造一个「备忘录」,每次算出某个子问题的答案后别急着返回,先记到「备忘录」里再返回;每次遇到一个子问题先去「备忘录」里查一查,如果发现之前已经解决过这个问题了,直接把答案拿出来用,不要再耗时去计算了。
一般使用一个数组充当这个「备忘录」,当然你也可以使用哈希表(字典),思想都是一样的。
int fib(int N) {
if (N < 1) return 0;
// 备忘录全初始化为 0
vector<int> memo(N + 1, 0);
return helper(memo, N);
}
int helper(vector<int>& memo, int n) {
if (n == 1 || n == 2) return 1;
if (memo[n] != 0) return memo[n];
// 未被计算过
memo[n] = helper(memo, n - 1) + helper(memo, n - 2);
return memo[n];
}
实际上,带「备忘录」的递归算法,把一棵存在巨量冗余的递归树通过「剪枝」,改造成了一幅不存在冗余的递归图,极大减少了子问题(即递归图中节点)的个数。
递归算法的时间复杂度怎么算?子问题个数乘以解决一个子问题需要的时间。
子问题个数,即图中节点的总数,由于本算法不存在冗余计算,子问题就是 f(1), f(2), f(3) … f(20),数量和输入规模 n = 20 成正比,所以子问题个数为 O(n)。
解决一个子问题的时间,同上,没有什么循环,时间为 O(1)。
所以,本算法的时间复杂度是 O(n)。比起暴力算法,是降维打击。
至此,带备忘录的递归解法的效率已经和动态规划一样了。实际上,这种解法和动态规划的思想已经差不多了,只不过这种方法叫做「自顶向下」,动态规划叫做「自底向上」。
啥叫「自顶向下」?注意我们刚才画的递归树(或者说图),是从上向下延伸,都是从一个规模较大的原问题比如说 f(20),向下逐渐分解规模,直到 f(1) 和 f(2) 触底,然后逐层返回答案,这就叫「自顶向下」。
啥叫「自底向上」?反过来,我们直接从最底下,最简单,问题规模最小的 f(1) 和 f(2) 开始往上推,直到推到我们想要的答案 f(20),这就是动态规划的思路,这也是为什么动态规划一般都脱离了递归,而是由循环迭代完成计算。
第三步:动态规划,重点!!
有了上一步「备忘录」的启发,我们可以把这个「备忘录」独立出来成为一张表,就叫做 DP table 吧,在这张表上完成「自底向上」的推算岂不美哉!
int fib(int N) {
vector<int> dp(N + 1, 0);
dp[1] = dp[2] = 1;
for (int i = 3; i <= N; i++)
dp[i] = dp[i - 1] + dp[i - 2];
return dp[N];
}

画个图就很好理解了,而且你发现这个 DP table 特别像之前那个「剪枝」后的结果,只是反过来算而已。实际上,带备忘录的递归解法中的「备忘录」,最终完成后就是这个 DP table,所以说这两种解法其实是差不多的,大部分情况下,效率也基本相同。
这里,引出 「动态转移方程」 这个名词,实际上就是描述问题结构的数学形式:
f ( n ) = { 1 , n = 1 , 2 f ( n − 1 ) + f ( n − 2 ) , n > 2 f(n) = \begin{cases} 1, n = 1, 2 \\ f(n - 1) + f(n - 2), n > 2 \end{cases} f(n)={1,n=1,2f(n−1)+f(n−2),n>2
为啥叫「状态转移方程」?为了听起来高端。你把 f(n) 想做一个状态 n,这个状态 n 是由状态 n - 1 和状态 n - 2 相加转移而来,这就叫状态转移,仅此而已。
你会发现,上面的几种解法中的所有操作,例如 return f(n - 1) + f(n - 2),dp[i] = dp[i - 1] + dp[i - 2],以及对备忘录或 DP table 的初始化操作,都是围绕这个方程式的不同表现形式。可见列出「状态转移方程」的重要性,它是解决问题的核心。很容易发现,其实状态转移方程直接代表着暴力解法。
千万不要看不起暴力解,动态规划问题最困难的就是第一步,写出状态转移方程,即这个暴力解。优化方法无非是用备忘录或者 DP table,再无奥妙可言。
空间优化:见下
动态规划,空间复杂度简化版
斐波那契数的边界条件是 F ( 0 ) = 0 F(0)=0 F(0)=0 和 F ( 1 ) = 1 F(1)=1 F(1)=1。当 n > 1 n>1 n>1 时,每一项的和都等于前两项的和,因此有如下递推关系:
F ( n ) = F ( n − 1 ) + F ( n − 2 ) F(n)=F(n-1)+F(n-2) F(n)=F(n−1)+F(n−2)
由于斐波那契数存在递推关系,因此可以使用动态规划求解。动态规划的状态转移方程即为上述递推关系,边界条件为 F ( 0 ) F(0) F(0) 和 F ( 1 ) F(1) F(1)。
根据状态转移方程和边界条件,可以得到时间复杂度和空间复杂度都是 O ( n ) O(n) O(n) 的实现。由于 F ( n ) F(n) F(n) 只和 F ( n − 1 ) F(n-1) F(n−1) 与 F ( n − 2 ) F(n-2) F(n−2) 有关,因此可以使用「滚动数组思想」把空间复杂度优化成 O ( 1 ) O(1) O(1)。
| p | q | r=p+q |
|---|---|---|
| 0 | 0 | 1 |
| p | q | r=p+q |
|---|---|---|
| 0 | 1 | 1 |
| p | q | r=p+q |
|---|---|---|
| 1 | 1 | 2 |
…以此类推
class Solution {
public:
int fib(int n) {
if (n < 2) {
return n;
}
int dp0 = 0, dp1 = 0, dp2 = 1;
for (int i = 2; i <= n; ++i) {
dp0 = dp1;
dp1 = dp2;
dp2 = dp0+dp1;
}
return dp2;
}
};
复杂度分析
- 时间复杂度:O(n)。
- 空间复杂度:O(1)。
1137. N-th Tribonacci Number 第 N 个泰波那契数
The Tribonacci sequence Tn is defined as follows:
T0 = 0, T1 = 1, T2 = 1, and Tn+3 = Tn + Tn+1 + Tn+2 for n >= 0.
Given n, return the value of Tn.
Example 1:
Input: n = 4
Output: 4
Explanation:
T_3 = 0 + 1 + 1 = 2
T_4 = 1 + 1 + 2 = 4
Example 2:
Input: n = 25
Output: 1389537
Constraints:
0 <= n <= 37
The answer is guaranteed to fit within a 32-bit integer, ie. answer <= 2^31 - 1.
我的方法:同斐波拉契数列解法,动规,滚动数组
class Solution {
public:
int tribonacci(int n) {
if (n<2) return n;
if (n==2) return 1;
int dp0 = 0, dp1 = 0, dp2 = 1, dp3 = 1;
for (int i=3; i<=n; i++)
{
dp0 = dp1;
dp1 = dp2;
dp2 = dp3;
dp4 = dp1+dp2+dp3;
}
return dp4;
}
};
70. Climbing Stairs 实际上等价于斐波那契数列
You are climbing a staircase. It takes n steps to reach the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
Example 1:
Input: n = 2
Output: 2
Explanation: There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps
3.
Example 2:
Input: n = 3
Output: 3
Explanation: There are three ways to climb to the top.
4. 1 step + 1 step + 1 step
5. 1 step + 2 steps
6. 2 steps + 1 step
Constraints:
1 <= n <= 45
我的解法:备忘录,自下而上
class Solution {
public:
int helper(vector<int>& memo, int n) {
if (n == 1 || n == 2) return n;
if (memo[n] != 0) return memo[n];
// 未被计算过
memo[n] = helper(memo, n - 1) + helper(memo, n - 2);
return memo[n];
}
int climbStairs(int n) {
vector<int> memo(n+1, 0);
return helper(memo, n);
}
};
凑零钱问题
动态规划的另一个重要特性「最优子结构」,怎么没有涉及?下面会涉及。斐波那契数列的例子严格来说不算动态规划,以上旨在演示算法设计螺旋上升的过程。当问题中要求求一个最优解或在代码中看到循环和 max、min 等函数时,十有八九,需要动态规划大显身手。下面,看第二个例子,凑零钱问题,有了上面的详细铺垫,这个问题会很快解决。
- 题目:给你 k 种面值的硬币,面值分别为 c1, c2 … ck,再给一个总金额 n,
问你最少需要几枚硬币凑出这个金额,如果不可能凑出,则回答 -1 。
比如说,k = 3,面值分别为1,2,5,总金额n = 11,那么最少需要3枚硬币,即11 = 5 + 5 + 1。
记住,要符合「最优子结构」,子问题间必须互相独立。为什么说它符合最优⼦结构呢?⽐如你想求 amount =11 时的最少硬币数(原问题),如果你知道凑出 amount = 10 的最少硬币数(⼦问题),你只需要把⼦问题的答案加⼀(再选⼀枚⾯值为 1 的硬币)就是原问题的答案,因为硬币的数量是没有限制的,⼦问题之间没有相互制,是互相独⽴的。
下面走流程。
一、暴力解法
首先是最困难的一步,写出状态转移方程,这个问题比较好写:
如何列出正确的状态转移⽅程?
- 先确定「状态」,也就是原问题和⼦问题中变化的变量。由于硬币数量⽆限,所以唯⼀的状态就是⽬标⾦额
amount。 - 然后确定 dp 函数的定义:当前的⽬标⾦额是
n,⾄少需要dp(n)个硬币凑出该⾦额。 - 然后确定「选择」并择优,也就是对于每个状态,可以做出什么选择改变当前状态。具体到这个问题,⽆论当的⽬标⾦额是多少,选择就是从⾯额列表
coins中选择⼀个硬币,然后⽬标⾦额就会减少: - 最后明确 base case,显然⽬标⾦额为 0 时,所需硬币数量为 0;当⽬标⾦额⼩于 0 时,⽆解,返回 -1:
d p ( n ) = { 0 , n = 0 − 1 , n < 0 m i n { d p ( n − c o i n ) + 1 ∣ c o i n ∈ c o i n s } , n > 0 dp(n) = \begin{cases} 0, n = 0 \\ -1, n < 0 \\ min\{dp(n - coin) + 1 | coin \in coins\}, n > 0 \end{cases} dp(n)=⎩⎪⎨⎪⎧0,n=0−1,n<0min{dp(n−coin)+1∣coin∈coins},n>0
其实,这个方程就用到了「最优子结构」性质:原问题的解由子问题的最优解构成。即 f(11) 由 f(10), f(9), f(6) 的最优解转移而来。
int coinChange(vector<int>& coins, int amount) {
// base case
if (amount == 0) return 0;
if (amount <0) return -1;
// 求最小值,初始化为正无穷
int ans = INT_MAX;
for (int coin : coins) {
int subProb = coinChange(coins, amount - coin); // 1、当amount-coin=1时,subprob=1
// 子问题无解
if (subProb == -1) continue;
ans = min(ans, subProb + 1); // 2、ans就是一个计步用的变量
}
return ans == INT_MAX ? -1 : ans;
}
⾄此,这个问题其实就解决了,只不过需要消除⼀下重叠⼦问题,⽐如 amount = 11, coins = {1,2,5} 时画出递归树:
时间复杂度分析:子问题总数 x 每个子问题的时间。
子问题总数为递归树节点个数,这个比较难看出来,是 O ( n k ) O(n^k) O(nk),总之是指数级别的。每个子问题中含有一个 for 循环,复杂度为 O ( k ) O(k) O(k)。所以总时间复杂度为 O ( k ∗ n k ) O(k*n^k) O(k∗nk),指数级别。
二、带备忘录的递归
int coinChange(vector<int>& coins, int amount) {
// 备忘录初始化为 -2
vector<int> memo(amount + 1, -2);
return helper(coins, amount, memo);
}
int helper(vector<int>& coins, int amount, vector<int>& memo) {
// base case
if (amount == 0) return 0;
if (amount <0) return -1;
// 查询备忘录
if (memo[amount] != -2) return memo[amount]; //
int ans = INT_MAX;
for (int coin : coins) {
int subProb = helper(coins, amount - coin, memo);
// 子问题无解
if (subProb == -1) continue;
ans = min(ans, subProb + 1);
}
// 记录本轮答案
memo[amount] = (ans == INT_MAX) ? -1 : ans;
return memo[amount];
}
三、动态规划
当然,我们也可以⾃底向上使⽤ dp table 来消除重叠⼦问题, dp 数组的定义和刚才 dp 函数类似,定义也是⼀样的:
int coinChange(vector<int>& coins, int amount) {
vector<int> dp(amount + 1, amount + 1);
dp[0] = 0;
for (int i = 1; i <= amount; i++) {
for (int coin : coins)
if (coin <= i)
dp[i] = min(dp[i], dp[i - coin] + 1);
}
return dp[amount] > amount ? -1 : dp[amount];
}
746. Min Cost Climbing Stairs
You are given an integer array cost where cost[i] is the cost of ith step on a staircase. Once you pay the cost, you can either climb one or two steps.
You can either start from the step with index 0, or the step with index 1.
Return the minimum cost to reach the top of the floor.
每个阶梯都有一定数量坨屎,一次只能跨一个或者两个阶梯,走到一个阶梯就要吃光上面的屎,问怎么走才能吃最少的屎?开局你选前两个阶梯的其中一个作为开头点,并吃光该阶梯的屎。
Example 1:
Input: cost = [10,15,20]
Output: 15
Explanation: You will start at index 1.
- Pay 15 and climb two steps to reach the top.
The total cost is 15.
Example 2:
Input: cost = [1,100,1,1,1,100,1,1,100,1]
Output: 6
Explanation: You will start at index 0.
- Pay 1 and climb two steps to reach index 2.
- Pay 1 and climb two steps to reach index 4.
- Pay 1 and climb two steps to reach index 6.
- Pay 1 and climb one step to reach index 7.
- Pay 1 and climb two steps to reach index 9.
- Pay 1 and climb one step to reach the top.
The total cost is 6.
Constraints:
2 <= cost.length <= 1000
0 <= cost[i] <= 999
方法一:动态规划
假设数组 cost \textit{cost} cost 的长度为 n,则 n 个阶梯分别对应下标 0 到 n−1,楼层顶部对应下标 n,问题等价于计算达到下标 n 的最小花费。可以通过动态规划求解。
创建长度为 n+1 的数组 dp \textit{dp} dp,其中 dp [ i ] \textit{dp}[i] dp[i] 表示达到下标 i 的最小花费。
由于可以选择下标 0 或 1 作为初始阶梯,因此有 dp [ 0 ] = dp [ 1 ] = 0 \textit{dp}[0]=\textit{dp}[1]=0 dp[0]=dp[1]=0。
当 2 ≤ i ≤ n 2 \le i \le n 2≤i≤n 时,可以从下标 i-1 使用 cost [ i − 1 ] \textit{cost}[i-1] cost[i−1] 的花费达到下标 i,或者从下标 i−2 使用 cost [ i − 2 ] \textit{cost}[i-2] cost[i−2]的花费达到下标 i。为了使总花费最小, dp [ i ] \textit{dp}[i] dp[i] 应取上述两项的最小值,因此状态转移方程如下:
dp [ i ] = min ( dp [ i − 1 ] + cost [ i − 1 ] , dp [ i − 2 ] + cost [ i − 2 ] ) \textit{dp}[i]=\min(\textit{dp}[i-1]+\textit{cost}[i-1],\textit{dp}[i-2]+\textit{cost}[i-2]) dp[i]=min(dp[i−1]+cost[i−1],dp[i−2]+cost[i−2])
依次计算 dp \textit{dp} dp 中的每一项的值,最终得到的 dp [ n ] \textit{dp}[n] dp[n] 即为达到楼层顶部的最小花费。
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
int n = cost.size();
vector<int> dp(n + 1);
dp[0] = dp[1] = 0;
for (int i = 2; i <= n; i++) {
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
}
return dp[n];
}
};
注意到当 i ≥ 2 i \ge 2 i≥2 时, dp [ i ] \textit{dp}[i] dp[i] 只和 dp [ i − 1 ] \textit{dp}[i-1] dp[i−1] 与 dp [ i − 2 ] \textit{dp}[i-2] dp[i−2] 有关,因此可以使用滚动数组的思想,将空间复杂度优化到 O(1)。
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
int n = cost.size();
int prev = 0, curr = 0;
for (int i = 2; i <= n; i++) {
int next = min(curr + cost[i - 1], prev + cost[i - 2]);
prev = curr;
curr = next;
}
return curr;
}
};
198. House Robber
You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security systems connected and it will automatically contact the police if two adjacent houses were broken into on the same night.
Given an integer array nums representing the amount of money of each house, return the maximum amount of money you can rob tonight without alerting the police.
Example 1:
Input: nums = [1,2,3,1]
Output: 4
Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.
Example 2:
Input: nums = [2,7,9,3,1]
Output: 12
Explanation: Rob house 1 (money = 2), rob house 3 (money = 9) and rob house 5 (money = 1).
Total amount you can rob = 2 + 9 + 1 = 12.
Constraints:
1 <= nums.length <= 100
0 <= nums[i] <= 400
方法:dp
首先考虑最简单的情况base case。
- 如果只有一间房屋,则偷窃该房屋,可以偷窃到最高总金额。
- 如果只有两间房屋,则由于两间房屋相邻,不能同时偷窃,只能偷窃其中的一间房屋,因此选择其中金额较高的房屋进行偷窃,可以偷窃到最高总金额。
如果房屋数量大于两间,应该如何计算能够偷窃到的最高总金额呢?对于第 k ( k > 2 ) k~(k>2) k (k>2)间房屋,有两个选项:
-
偷窃第
k间房屋,那么就不能偷窃第k-1间房屋,偷窃总金额为前k-2间房屋的最高总金额与第k间房屋的金额之和。 -
不偷窃第
k间房屋,偷窃总金额为前k-1间房屋的最高总金额。
在两个选项中选择偷窃总金额较大的选项,该选项对应的偷窃总金额即为前 k 间房屋能偷窃到的最高总金额。
用 dp [ i ] \textit{dp}[i] dp[i] 表示前 i 间房屋能偷窃到的最高总金额,那么就有如下的状态转移方程:
dp [ i ] = max ( dp [ i − 2 ] + nums [ i ] , dp [ i − 1 ] ) \textit{dp}[i] = \max(\textit{dp}[i-2]+\textit{nums}[i], \textit{dp}[i-1]) dp[i]=max(dp[i−2]+nums[i],dp[i−1])
边界条件为:
{ dp [ 0 ] = nums [ 0 ] 只 有 一 间 房 屋 , 则 偷 窃 该 房 屋 dp [ 1 ] = max ( nums [ 0 ] , nums [ 1 ] ) 只 有 两 间 房 屋 , 选 择 其 中 金 额 较 高 的 房 屋 进 行 偷 窃 \begin{cases} \textit{dp}[0] = \textit{nums}[0] & 只有一间房屋,则偷窃该房屋 \\ \textit{dp}[1] = \max(\textit{nums}[0], \textit{nums}[1]) & 只有两间房屋,选择其中金额较高的房屋进行偷窃 \end{cases} {dp[0]=nums[0]dp[1]=max(nums[0],nums[1])只有一间房屋,则偷窃该房屋只有两间房屋,选择其中金额较高的房屋进行偷窃
只有一间房屋,则偷窃该房屋
只有两间房屋,选择其中金额较高的房屋进行偷窃
最终的答案即为 dp [ n − 1 ] \textit{dp}[n-1] dp[n−1],其中 n 是数组的长度。
class Solution {
public:
int rob(vector<int>& nums) {
int n = nums.size();
if (n==1) return nums[0];
int i1=0, i2=nums[0], i3=max(nums[0], nums[1]);
// vector v(n, 0);
// v[0] = nums[0];
// v[1] = max(nums[0], nums[1]);
for (int i=2; i<n; i++)
{
i1 = i2;
i2 = i3;
i3 = max(i1+nums[i], i2);
// v[i] = max(v[i-2]+nums[i], v[i-1]);
}
return i3;//v[n-1];
}
};
213. House Robber II
You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed. All houses at this place are arranged in a circle. That means the first house is the neighbor of the last one. Meanwhile, adjacent houses have a security system connected, and it will automatically contact the police if two adjacent houses were broken into on the same night.
Given an integer array nums representing the amount of money of each house, return the maximum amount of money you can rob tonight without alerting the police.
这道题是「198. 打家劫舍」的进阶,和第 198 题的不同之处是,这道题中的房屋是首尾相连的,第一间房屋和最后一间房屋相邻,因此第一间房屋和最后一间房屋不能在同一晚上偷窃。
Example 1:
Input: nums = [2,3,2]
Output: 3
Explanation: You cannot rob house 1 (money = 2) and then rob house 3 (money = 2), because they are adjacent houses.
Example 2:
Input: nums = [1,2,3,1]
Output: 4
Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.
Example 3:
Input: nums = [1,2,3]
Output: 3
Constraints:
1 <= nums.length <= 100
0 <= nums[i] <= 1000
方法:dp
注意到当房屋数量不超过两间时,最多只能偷窃一间房屋,因此不需要考虑首尾相连的问题。如果房屋数量大于两间,就必须考虑首尾相连的问题,第一间房屋和最后一间房屋不能同时偷窃。
如何才能保证第一间房屋和最后一间房屋不同时偷窃呢?如果偷窃了第一间房屋,则不能偷窃最后一间房屋,因此偷窃房屋的范围是第一间房屋到最后第二间房屋;如果偷窃了最后一间房屋,则不能偷窃第一间房屋,因此偷窃房屋的范围是第二间房屋到最后一间房屋。
假设数组 nums \textit{nums} nums的长度为 n。如果不偷窃最后一间房屋,则偷窃房屋的下标范围是 [0, n-2];如果不偷窃第一间房屋,则偷窃房屋的下标范围是 [1, n-1]。在确定偷窃房屋的下标范围之后,即可用第 198 题的方法解决。对于两段下标范围分别计算可以偷窃到的最高总金额,其中的最大值即为在 n 间房屋中可以偷窃到的最高总金额。
分别取 ( start , end ) = ( 0 , n − 2 ) (\textit{start},\textit{end})=(0,n-2) (start,end)=(0,n−2) 和 ( start , end ) = ( 1 , n − 1 ) (\textit{start},\textit{end})=(1,n-1) (start,end)=(1,n−1) 进行计算,取两个 dp [ end ] \textit{dp}[\textit{end}] dp[end] 中的最大值,即可得到最终结果。
class Solution {
public:
int robRange(vector<int>& nums, int start, int end) {
int dp0 = 0, dp1 = nums[start], dp2 = max(nums[start], nums[start + 1]);
for (int i = start + 2; i <= end; i++) {
dp0 = dp1;
dp1 = dp2;
dp2 = max(dp0 + nums[i], dp1);
}
return dp2;
}
int rob(vector<int>& nums) {
int length = nums.size();
if (length == 1) {
return nums[0];
} else if (length == 2) {
return max(nums[0], nums[1]);
}
return max(robRange(nums, 0, length - 2), robRange(nums, 1, length - 1));
}
};
740. Delete and Earn
You are given an integer array nums. You want to maximize the number of points you get by performing the following operation any number of times:
Pick any nums[i] and delete it to earn nums[i] points. Afterwards, you must delete every element equal to nums[i] - 1 and every element equal to nums[i] + 1.
Return the maximum number of points you can earn by applying the above operation some number of times.
Example 1:
Input: nums = [3,4,2]
Output: 6
Explanation: You can perform the following operations:
- Delete 4 to earn 4 points. Consequently, 3 is also deleted. nums = [2].
- Delete 2 to earn 2 points. nums = [].
You earn a total of 6 points.
Example 2:
Input: nums = [2,2,3,3,3,4]
Output: 9
Explanation: You can perform the following operations:
- Delete a 3 to earn 3 points. All 2's and 4's are also deleted. nums = [3,3].
- Delete a 3 again to earn 3 points. nums = [3].
- Delete a 3 once more to earn 3 points. nums = [].
You earn a total of 9 points.
Constraints:
1 <= nums.length <= 2 * 10^4
1 <= nums[i] <= 10^4
我的解法:动态规划
声明一个具有 1 0 4 + 1 10^4+1 104+1 size 的vector,将nums中所含有的值,填入该vector,可转化为打家劫舍问题,相邻位置无法同时加入迭代公式。
class Solution {
public:
int deleteAndEarn(vector<int>& nums) {
int length = nums.size();
vector<int> nums_new(10001, 0);
for (auto& i : nums)
{
nums_new[i] += i;
}
if (length==1) return nums[0];
int dp0 = 0, dp1 = nums_new[0], dp2 = max(nums_new[0], nums_new[1]);
for (int i = 2; i<nums_new.size(); ++i)
{
dp0 = dp1;
dp1 = dp2;
dp2 = max(dp0+nums_new[i], dp1);
}
return dp2;
}
};
复杂度分析:
时间:O(10001+n)
空间:O(10001)
改进,vector 内存优化,尽量减少100001的内存。见下 处
方法二:官解dp
根据题意,在选择了元素 x 后,该元素以及所有等于 x-1 或 x+1 的元素会从数组中删去。若还有多个值为 x 的元素,由于所有等于 x-1 或 x+1 的元素已经被删除,我们可以直接删除 x 并获得其点数。因此若选择了 x,所有等于 x 的元素也应一同被选择,以尽可能多地获得点数。
记元素 x 在数组中出现的次数为 c x c_x cx,我们可以用一个数组 sum 记录数组 nums \textit{nums} nums 中所有相同元素之和,即 sum [ x ] = x ⋅ c x \textit{sum}[x]=x\cdot c_x sum[x]=x⋅cx。若选择了 x,则可以获取 sum [ x ] \textit{sum}[x] sum[x] 的点数,且无法再选择 x-1 和 x+1。这与「198. 打家劫舍」是一样的,在统计出 sum \textit{sum} sum 数组后,读者可参考「198. 打家劫舍的官方题解」中的动态规划过程计算出答案。
class Solution {
private:
int rob(vector<int> &nums) {
int size = nums.size();
int dp0 = 0, dp1 = nums[0], dp2 = max(nums[0], nums[1]);
for (int i = 2; i < size; i++) {
dp0 = dp1;
dp1 = dp2;
dp2 = max(dp0 + nums[i], dp1);
}
return dp2;
}
public:
int deleteAndEarn(vector<int> &nums) {
int maxVal = 0;
for (int val : nums) {
maxVal = max(maxVal, val); //
}
vector<int> sum(maxVal + 1); //
for (int val : nums) {
sum[val] += val;
}
return rob(sum);
}
};
复杂度分析:
- 时间:O(n+m),其中n为nums的长度,m 是 nums \textit{nums} nums 中元素的最大值。
- 空间复杂度:O(M)。
55. Jump Game
You are given an integer array nums. You are initially positioned at the array’s first index, and each element in the array represents your maximum jump length at that position.
Return true if you can reach the last index, or false otherwise.
Example 1:
Input: nums = [2,3,1,1,4]
Output: true
Explanation: Jump 1 step from index 0 to 1, then 3 steps to the last index.
Example 2:
Input: nums = [3,2,1,0,4]
Output: false
Explanation: You will always arrive at index 3 no matter what. Its maximum jump length is 0, which makes it impossible to reach the last index.
Constraints:
1 <= nums.length <= 104
0 <= nums[i] <= 105
官解:贪心法
设想一下,对于数组中的任意一个位置 y,我们如何判断它是否可以到达?根据题目的描述,只要存在一个位置 x,它本身可以到达,并且它跳跃的最大长度为 x + nums [ x ] x + \textit{nums}[x] x+nums[x],这个值大于等于 y,即 x + nums [ x ] ≥ y x + \textit{nums}[x] \geq y x+nums[x]≥y,那么位置 y 也可以到达。
换句话说,对于每一个可以到达的位置 x,它使得 x + 1 , x + 2 , ⋯ , x + nums [ x ] x+1, x+2, \cdots, x+\textit{nums}[x] x+1,x+2,⋯,x+nums[x] 这些连续的位置都可以到达。
这样以来,我们依次遍历数组中的每一个位置,并实时维护 最远可以到达的位置。对于当前遍历到的位置 x,如果它在 最远可以到达的位置 的范围内,那么我们就可以从起点通过若干次跳跃到达该位置,因此我们可以用 x + nums [ x ] x + \textit{nums}[x] x+nums[x] 更新 最远可以到达的位置。
在遍历的过程中,如果 最远可以到达的位置 大于等于数组中的最后一个位置,那就说明最后一个位置可达,我们就可以直接返回 True 作为答案。反之,如果在遍历结束后,最后一个位置仍然不可达,我们就返回 False 作为答案。
以题目中的示例一:
[2, 3, 1, 1, 4]
我们一开始在位置 0,可以跳跃的最大长度为 2,因此最远可以到达的位置被更新为 2;
我们遍历到位置 1,由于 1 ≤ 2 1 \leq 2 1≤2,因此位置 1 可达。我们用 1 加上它可以跳跃的最大长度 3,将最远可以到达的位置更新为 4。由于 4 大于等于最后一个位置 4,因此我们直接返回 True。
我们再来看看题目中的示例二
[3, 2, 1, 0, 4]
我们一开始在位置 0,可以跳跃的最大长度为 3,因此最远可以到达的位置被更新为 3;
我们遍历到位置 1,由于 1 ≤ 3 1 \leq 3 1≤3,因此位置 1 可达,加上它可以跳跃的最大长度 2 得到 3,没有超过最远可以到达的位置;
位置 2、位置 3 同理,最远可以到达的位置不会被更新;
我们遍历到位置 4,由于 4 > 3,因此位置 4 不可达,我们也就不考虑它可以跳跃的最大长度了。
在遍历完成之后,位置 4 仍然不可达,因此我们返回 False。
-
我们一开始在位置 0,可以跳跃的最大长度为 3,因此最远可以到达的位置被更新为 3;
-
我们遍历到位置 1,由于 1 ≤ 3 1 \leq 3 1≤3,因此位置 1 可达,加上它可以跳跃的最大长度 2 得到 3,没有超过最远可以到达的位置;
-
位置 2、位置 3 同理,最远可以到达的位置不会被更新;
-
我们遍历到位置 4,由于 4 > 3,因此位置 4 不可达,我们也就不考虑它可以跳跃的最大长度了。
在遍历完成之后,位置 4 仍然不可达,因此我们返回 False。
class Solution {
public:
bool canJump(vector<int>& nums) {
int n = nums.size();
int rightmost = 0;
for (int i = 0; i < n; ++i) {
if (i <= rightmost) { // 如果第i个位置位于我们之前最远能抵达的位置,则认为可到达,
rightmost = max(rightmost, i + nums[i]);// 故,我们可从该处开始跳跃最大位置
if (rightmost >= n - 1) {
return true;
}
}
}
return false;
}
};
复杂度分析
时间复杂度:O(n),其中 n 为数组的大小。只需要访问 nums 数组一遍,共 n 个位置。
空间复杂度:O(1),不需要额外的空间开销。
方法二:反向查找
由题目描述,我们需要达到最后一个下标,那么最后一个下标的数字其实是可以不用考虑的。那么我们可以假设只有两个数字(比如 [2, 4]),这个时候第一个数字如果是大于等于 1 的数就成立;如果是三个数字的话(比如 [3, 0, 4]),第一个数字大于等于 22 时成立。依此类推,一个数字可以到达的位置必须是这个数字标记的长度值,有:nums[i] >= j 成立时才可以到达后面第 j 个目标。
有了上述前提,假设现在只有最后两位数字,在判断出倒数第 2 位数字可以到达最后一位时,我们只需要看剩下的部分,如果可以到达倒数第 2 位,那么整体就可以到达最后一位数字。
我们记录一个最后一位的下标,然后依次向前寻找满足跳跃条件的下标,并将该下标与记录的下标替换。重复这个过程直到判断了 nums 的第一个下标为止,最后判断记录值是否为第一个下标,也就是 0 ,如果不是 0 返回 false。
class Solution {
public:
bool canJump(vector<int>& nums) {
int end = nums.size()-1;//必须达到的末尾
for(int i=nums.size()-2; i>=0; i--) {
//i位置能否达到end位置
if(end - i <= nums[i])
end = i;
}
return end==0;
}
};
该过程时间复杂度为 O(n),空间复杂度为 O(1) 。
45. Jump Game II
Given an array of non-negative integers nums, you are initially positioned at the first index of the array.
Each element in the array represents your maximum jump length at that position.
Your goal is to reach the last index in the minimum number of jumps.
You can assume that you can always reach the last index.
Example 1:
Input: nums = [2,3,1,1,4]
Output: 2
Explanation: The minimum number of jumps to reach the last index is 2. Jump 1 step from index 0 to 1, then 3 steps to the last index.
Example 2:
Input: nums = [2,3,0,1,4]
Output: 2
Constraints:
1 <= nums.length <= 104
0 <= nums[i] <= 1000
这道题是典型的贪心算法,通过局部最优解得到全局最优解。以下两种方法都是使用贪心算法实现,只是贪心的策略不同。
方法一:反向查找出发位置
我们的目标是到达数组的最后一个位置,因此我们可以考虑最后一步跳跃前所在的位置,该位置通过跳跃能够到达最后一个位置。
如果有多个位置通过跳跃都能够到达最后一个位置,那么我们应该如何进行选择呢?直观上来看,我们可以「贪心」地选择距离最后一个位置最远的那个位置,也就是对应下标最小的那个位置。因此,我们可以从左到右遍历数组,选择第一个满足要求的位置。
找到最后一步跳跃前所在的位置之后,我们继续贪心地寻找倒数第二步跳跃前所在的位置,以此类推,直到找到数组的开始位置。
使用这种方法编写的 C++ 和 Python 代码会超出时间限制,因此我们只给出 Java 和 Go 代码。
class Solution {
public int jump(int[] nums) {
int position = nums.length - 1;
int steps = 0;
while (position > 0) {
for (int i = 0; i < position; i++) {
if (i + nums[i] >= position) {
position = i;
steps++;
break;
}
}
}
return steps;
}
}
复杂度分析
- 时间复杂度: O ( n 2 ) O(n^2) O(n2),其中 n 是数组长度。有两层嵌套循环,在最坏的情况下,例如数组中的所有元素都是 1,position 需要遍历数组中的每个位置,对于 position 的每个值都有一次循环。
- 空间复杂度: O ( 1 ) O(1) O(1)。
方法二:正向查找可到达的最大位置
方法一虽然直观,但是时间复杂度比较高,有没有办法降低时间复杂度呢?
如果我们「贪心」地进行正向查找,每次找到可到达的最远位置,就可以在线性时间内得到最少的跳跃次数。
例如,对于数组 [2,3,1,2,4,2,3],初始位置是下标 0,从下标 0 出发,最远可到达下标 2。下标 0 可到达的位置中,下标 1 的值是 3,从下标 1 出发可以达到更远的位置,因此第一步到达下标 1。
从下标 1 出发,最远可到达下标 4。下标 1 可到达的位置中,下标 4 的值是 4 ,从下标 4 出发可以达到更远的位置,因此第二步到达下标 4。
在具体的实现中,我们维护当前能够到达的最大下标位置,记为边界。我们从左到右遍历数组,到达边界时,更新边界并将跳跃次数增加 1。
在遍历数组时,我们不访问最后一个元素,这是因为在访问最后一个元素之前,我们的边界一定大于等于最后一个位置,否则就无法跳到最后一个位置了。如果访问最后一个元素,在边界正好为最后一个位置的情况下,我们会增加一次「不必要的跳跃次数」,因此我们不必访问最后一个元素。
class Solution {
public:
int jump(vector<int>& nums) {
int maxPos = 0, n = nums.size(), end = 0, step = 0;
for (int i = 0; i < n - 1; ++i) {
if (maxPos >= i) {
maxPos = max(maxPos, i + nums[i]);
if (i == end) { //当遍历i到上次跳跃的最远距离时,
end = maxPos; //记录本次i点跳跃时的最远位置
++step; //同时我们所需要跳跃的次数+1
}
}
}
return step;
}
};
复杂度分析
时间复杂度:O(n),其中 n 是数组长度。
空间复杂度:O(1)。
53. Maximum Subarray 最大子序和
Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.
A subarray is a contiguous part of an array.
Example 1:
Input: nums = [-2,1,-3,4,-1,2,1,-5,4]
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.
Example 2:
Input: nums = [1]
Output: 1
Example 3:
Input: nums = [5,4,-1,7,8]
Output: 23
Constraints:
1 <= nums.length <= 105
-104 <= nums[i] <= 104
Follow up: If you have figured out the O(n) solution, try coding another solution using the divide and conquer approach, which is more subtle.
方法一:动态规划
假设 nums \textit{nums} nums数组的长度是 n,下标从 0 到 n-1。
我们用 f(i) 代表以第 i 个数结尾的「连续子数组的最大和」,那么很显然我们要求的答案就是:
max 0 ≤ i ≤ n − 1 { f ( i ) } \max_{0 \leq i \leq n-1} \{ f(i) \} 0≤i≤n−1max{f(i)}
因此我们只需要求出每个位置的 f(i),然后返回 f 数组中的最大值即可。那么我们如何求 f(i) 呢?我们可以考虑 nums [ i ] \textit{nums}[i] nums[i] 单独成为一段还是加入 f(i-1) 对应的那一段,这取决于 nums [ i ] \textit{nums}[i] nums[i] 和 f ( i − 1 ) + nums [ i ] f(i-1) + \textit{nums}[i] f(i−1)+nums[i] 的大小,我们希望获得一个比较大的,于是可以写出这样的动态规划转移方程:
f ( i ) = max { f ( i − 1 ) + nums [ i ] , nums [ i ] } f(i) = \max \{ f(i-1) + \textit{nums}[i], \textit{nums}[i] \} f(i)=max{f(i−1)+nums[i],nums[i]}
不难给出一个时间复杂度 O(n)、空间复杂度 O(n) 的实现,即用一个 f 数组来保存 f(i) 的值,用一个循环求出所有 f(i)。考虑到 f(i) 只和 f(i-1) 相关,于是我们可以只用一个变量 pre \textit{pre} pre 来维护对于当前 f(i) 的 f(i-1) 的值是多少,从而让空间复杂度降低到 O(1),这有点类似「滚动数组」的思想。
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int dp0 = 0, dp1 = nums[0];
for (const auto &x: nums) {
dp0 = max(dp0 + x, x); // dp方程
dp1 = max(dp1, dp0); // 此处用maxAns记录遍历过程中出现的最大子序和
}
return maxAns;
}
// if (nums.size()==1) return nums[0];
// int dp0 = 0, dp1 = nums[0], dp2 = max(dp1 + nums[1], nums[1]);
// int maxrestore = max(dp1, dp2);
// for (int i = 2; i < nums.size(); ++i)
// {
// dp0 = dp1; dp1 = dp2;
// dp2 = max(dp1 + nums[i], nums[i]);
// maxrestore = max(dp2, maxrestore);
// }
// return maxrestore;
};
复杂度
- 时间复杂度:
O(n),其中n为 nums \textit{nums} nums 数组的长度。我们只需要遍历一遍数组即可求得答案。 - 空间复杂度:
O(1)。我们只需要常数空间存放若干变量。
方法二:分治 (待理解
)
这个分治方法类似于「线段树求解最长公共上升子序列问题」的 pushUp 操作。 也许读者还没有接触过线段树,没有关系,方法二的内容假设你没有任何线段树的基础。当然,如果读者有兴趣的话,推荐阅读线段树区间合并法解决多次询问的「区间最长连续上升序列问题」和「区间最大子段和问题」,还是非常有趣的。
我们定义一个操作 get(a, l, r) 表示查询 a 序列 [l,r] 区间内的最大子段和,那么最终我们要求的答案就是 get(nums, 0, nums.size() - 1)。如何分治实现这个操作呢?对于一个区间 [l,r],我们取 m = ⌊ l + r 2 ⌋ m = \lfloor \frac{l + r}{2} \rfloor m=⌊2l+r⌋,对区间 [l,m] 和 [m+1,r] 分治求解。当递归逐层深入直到区间长度缩小为 11 的时候,递归「开始回升」。这个时候我们考虑如何通过 [l,m] 区间的信息和 [m+1,r] 区间的信息合并成区间 [l,r] 的信息。最关键的两个问题是:
-
我们要维护区间的哪些信息呢?
-
我们如何合并这些信息呢?
对于一个区间[l,r],我们可以维护四个量: -
lSum \textit{lSum} lSum表示
[l,r]内以l为左端点的最大子段和 -
\textit{rSum}$表示
[l,r]内以r为右端点的最大子段和 -
\textit{mSum}$表示
[l,r]内的最大子段和 -
\textit{iSum}$表示
[l,r]的区间和
以下简称 [l,m] 为 [l,r] 的「左子区间」,[m+1,r] 为 [l,r] 的「右子区间」。我们考虑如何维护这些量呢(如何通过左右子区间的信息合并得到 [l,r] 的信息)?对于长度为 1 的区间 [i, i],四个量的值都和 nums [ i ] \textit{nums}[i] nums[i] 相等。对于长度大于 1 的区间:
首先最好维护的是 iSum \textit{iSum} iSum,区间 [l,r] 的 iSum \textit{iSum} iSum就等于「左子区间」的 iSum \textit{iSum} iSum加上「右子区间」的 iSum \textit{iSum} iSum。
对于 [l,r] 的 lSum \textit{lSum} lSum,存在两种可能,它要么等于「左子区间」的 lSum \textit{lSum} lSum,要么等于「左子区间」的 iSum \textit{iSum} iSum 加上「右子区间」的 lSum \textit{lSum} lSum,二者取大。
对于 [l,r] 的 rSum \textit{rSum} rSum,同理,它要么等于「右子区间」的 rSum \textit{rSum} rSum,要么等于「右子区间」的 iSum \textit{iSum} iSum 加上「左子区间」的 rSum \textit{rSum} rSum,二者取大。
当计算好上面的三个量之后,就很好计算 [l,r] 的 mSum \textit{mSum} mSum 了。我们可以考虑 [l,r] 的 mSum \textit{mSum} mSum 对应的区间是否跨越 m——它可能不跨越 m,也就是说 [l,r] 的 mSum \textit{mSum} mSum 可能是「左子区间」的 mSum \textit{mSum} mSum 和 「右子区间」的 mSum \textit{mSum} mSum 中的一个;它也可能跨越 m,可能是「左子区间」的 rSum \textit{rSum} rSum 和 「右子区间」的 lSum \textit{lSum} lSum 求和。三者取大。
这样问题就得到了解决。
918. Maximum Sum Circular Subarray
Given a circular integer array nums of length n, return the maximum possible sum of a non-empty subarray of nums.
A circular array means the end of the array connects to the beginning of the array. Formally, the next element of nums[i] is nums[(i + 1) % n] and the previous element of nums[i] is nums[(i - 1 + n) % n].
A subarray may only include each element of the fixed buffer nums at most once. Formally, for a subarray nums[i], nums[i + 1], …, nums[j], there does not exist i <= k1, k2 <= j with k1 % n == k2 % n.
Example 1:
Input: nums = [1,-2,3,-2]
Output: 3
Explanation: Subarray [3] has maximum sum 3.
Example 2:
Input: nums = [5,-3,5]
Output: 10
Explanation: Subarray [5,5] has maximum sum 5 + 5 = 10.
Example 3:
Input: nums = [-3,-2,-3]
Output: -2
Explanation: Subarray [-2] has maximum sum -2.
Constraints:
n == nums.length
1 <= n <= 3 * 104
-3 * 104 <= nums[i] <= 3 * 104
我的思路:对每个位置都进行一次53. Maximum Subarray 最大子序和的动态规划 超时了❌
int maxSubarraySumCircular(vector<int>& nums) {
int n = nums.size();
int dp0, dp1;
int dp2 = INT_MIN;
//if (n == 1) return nums[0];
for (int j = 0; j < n; ++j)
{
dp0 = 0, dp1 = nums[j];
for (int i = j; i < j + n; ++i)
{
dp0 = max(dp0 + nums[i % n], nums[i % n]);
dp1 = max(dp1, dp0);
dp2 = max(dp2, dp1);
}
}
return dp2;
}
时间复杂度: O ( n 2 ) O(n^2) O(n2)
空间复杂度:1
方法一:转化法
这题一共有两种情况(也就是相当于比53题多了一种最大子数组和是首尾连接的情况)
下面的这个子数组指最大和的子数组
第一种情况:这个子数组不是环状的,就是说首尾不相连。
第二种情况:这个子数组一部分在首部,一部分在尾部,
我们可以将这二种情况转换成最下下面的一种情况
如下图:
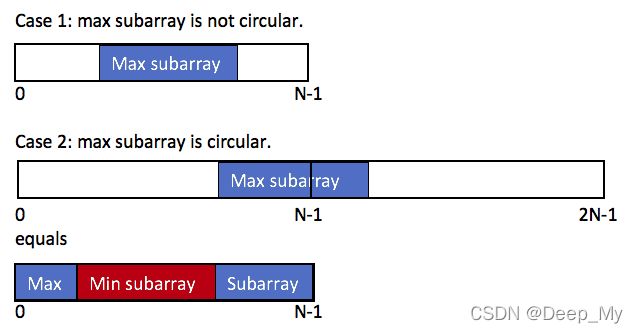
所以这最大的环形子数组和 = max(最大子数组和,数组总和-最小子数组和)
证明
证明一下第二种情况(最大子数组是环形的)
- max(前缀数组+后缀数组)
= max(数组总和 - subarray) subarray指的是前缀数组和后缀数组中间的数组
= 数组总和 + max(-subarray) 数组总和是不变的,直接提出来
= 数组总和 - min(subarry)
极端情况:如果说这数组的所有数都是负数,那么上面的公式还需要变一下,因为这种情况,对于上面的第一种情况sum会等于数组中的最大值,而对二种情况sum=0(最小的子数组就是本数组,total-total=0)。所以多加一个case,判断最大子数组和是否小于0,小于0,直接返回该maxSubArray
int maxSubarraySumCircular(vector<int>& A) {
int total = 0, maxSum = A[0], curMax = 0, minSum = A[0], curMin = 0;
for (int& a : A) {
curMax = max(curMax + a, a);
maxSum = max(maxSum, curMax);
curMin = min(curMin + a, a);
minSum = min(minSum, curMin);
total += a;
}
return maxSum > 0 ? max(maxSum, total - minSum) : maxSum;
}
152. Maximum Product Subarray
Given an integer array nums, find a contiguous non-empty subarray within the array that has the largest product, and return the product.
The test cases are generated so that the answer will fit in a 32-bit integer.
A subarray is a contiguous subsequence of the array.
Example 1:
Input: nums = [2,3,-2,4]
Output: 6
Explanation: [2,3] has the largest product 6.
Example 2:
Input: nums = [-2,0,-1]
Output: 0
Explanation: The result cannot be 2, because [-2,-1] is not a subarray.
Constraints:
1 <= nums.length <= 2 * 104
-10 <= nums[i] <= 10
The product of any prefix or suffix of nums is guaranteed to fit in a 32-bit integer.
方法一:动态规划
思路和算法
如果我们用 f max ( i ) f_{\max}(i) fmax(i) 来表示以第 i 个元素结尾的乘积最大子数组的乘积,a 表示输入参数 nums,那么根据「53. 最大子序和」的经验,我们很容易推导出这样的状态转移方程:
f max ( i ) = max i = 1 n { f ( i − 1 ) × a i , a i } f_{\max}(i) = \max_{i = 1}^{n} \{ f(i - 1) \times a_i, a_i \} fmax(i)=i=1maxn{f(i−1)×ai,ai}
它表示以第 i 个元素结尾的乘积最大子数组的乘积可以考虑 a i a_i ai 加入前面的 f max ( i − 1 ) f_{\max}(i - 1) fmax(i−1) 对应的一段,或者单独成为一段,这里两种情况下取最大值。求出所有的 f max ( i ) f_{\max}(i) fmax(i) 之后选取最大的一个作为答案。
可是在这里,这样做是错误的。为什么呢?
因为这里的定义并不满足「最优子结构」。具体地讲,如果 a = { 5 , 6 , − 3 , 4 , − 3 } a = \{ 5, 6, -3, 4, -3 \} a={5,6,−3,4,−3},那么此时 f max f_{\max} fmax 对应的序列是 { 5 , 30 , − 3 , 4 , − 3 } \{ 5, 30, -3, 4, -3 \} {5,30,−3,4,−3},按照前面的算法我们可以得到答案为 30 30 30,即前两个数的乘积,而实际上答案应该是全体数字的乘积。我们来想一想问题出在哪里呢?问题出在最后一个 − 3 -3 −3 所对应的 f max f_{\max} fmax 的值既不是 − 3 -3 −3,也不是 4 × − 3 4 \times -3 4×−3,而是 5 × 30 × ( − 3 ) × 4 × ( − 3 ) 5 \times 30 \times (-3) \times 4 \times (-3) 5×30×(−3)×4×(−3)。所以我们得到了一个结论:当前位置的最优解未必是由前一个位置的最优解转移得到的。
我们可以根据正负性进行分类讨论。
- 考虑当前位置如果是一个负数的话,那么我们希望以它前一个位置结尾的某个段的积也是个负数,这样就可以负负得正,并且我们希望这个积尽可能「负得更多」,即尽可能小。
- 如果当前位置是一个正数的话,我们更希望以它前一个位置结尾的某个段的积也是个正数,并且希望它尽可能地大。
于是这里我们可以再维护一个 f min f_{\min} fmin,它表示以第 i 个元素结尾的乘积最小子数组的乘积,那么我们可以得到这样的动态规划转移方程:
f max ( i ) = max i = 1 n { f max ( i − 1 ) × a i , f min ( i − 1 ) × a i , a i } f min ( i ) = min i = 1 n { f max ( i − 1 ) × a i , f min ( i − 1 ) × a i , a i } \begin{aligned} f_{\max}(i) &= \max_{i = 1}^{n} \{ f_{\max}(i - 1) \times a_i, f_{\min}(i - 1) \times a_i, a_i \} \\ f_{\min}(i) &= \min_{i = 1}^{n} \{ f_{\max}(i - 1) \times a_i, f_{\min}(i - 1) \times a_i, a_i \} \end{aligned} fmax(i)fmin(i)=i=1maxn{fmax(i−1)×ai,fmin(i−1)×ai,ai}=i=1minn{fmax(i−1)×ai,fmin(i−1)×ai,ai}
它代表第 i 个元素结尾的乘积最大子数组的乘积 f max ( i ) f_{\max}(i) fmax(i) ,可以考虑把 a i a_i ai 加入第 i − 1 i - 1 i−1 个元素结尾的乘积最大或最小的子数组的乘积中,二者加上 a i a_i ai,三者取大,就是第 i i i 个元素结尾的乘积最大子数组的乘积。第 i i i 个元素结尾的乘积最小子数组的乘积 f min ( i ) f_{\min}(i) fmin(i)同理。
不难给出这样的实现:
class Solution {
public:
int maxProduct(vector<int>& nums) {
vector <int> maxF(nums), minF(nums);// 注意,此处为复制nums数组
for (int i = 1; i < nums.size(); ++i) {
maxF[i] = max(maxF[i - 1] * nums[i], max(nums[i], minF[i - 1] * nums[i]));
minF[i] = min(minF[i - 1] * nums[i], min(nums[i], maxF[i - 1] * nums[i]));
}
return *max_element(maxF.begin(), maxF.end());
}
int maxProduct(vector<int>& nums) {
int n = nums.size();
vector<int> vmin(n), vmax(n);
vmin[0] = vmax[0] = nums[0];
for (int i = 1; i < n; ++i)
{
vmax[i] = max(vmax[i - 1] * nums[i], max(vmin[i - 1] * nums[i], nums[i]));
vmin[i] = min(vmin[i - 1] * nums[i], min(vmax[i - 1] * nums[i], nums[i]));
}
return *max_element(vmax.begin(), vmax.end());
}
};
易得这里的渐进时间复杂度和渐进空间复杂度都是 O(n)
考虑优化空间。
由于第 i 个状态只和第 i - 1 个状态相关,根据「滚动数组」思想,我们可以只用两个变量来维护 i - 1 时刻的状态,一个维护 f max f_{\max} fmax,一个维护 f min f_{\min} fmin。细节参见代码。
class Solution {
public:
int maxProduct(vector<int>& nums) {
int maxF = nums[0], minF = nums[0], ans = nums[0];
for (int i = 1; i < nums.size(); ++i) {
int mx = maxF, mn = minF;
maxF = max(mx * nums[i], max(nums[i], mn * nums[i]));
minF = min(mn * nums[i], min(nums[i], mx * nums[i]));
ans = max(maxF, ans);
}
return ans;
}
};
复杂度分析
记 nums 元素个数为 n。
- 时间复杂度:程序一次循环遍历了 nums,故渐进时间复杂度为 O(n)。
- 空间复杂度:优化后只使用常数个临时变量作为辅助空间,与 n 无关,故渐进空间复杂度为 O(1)。