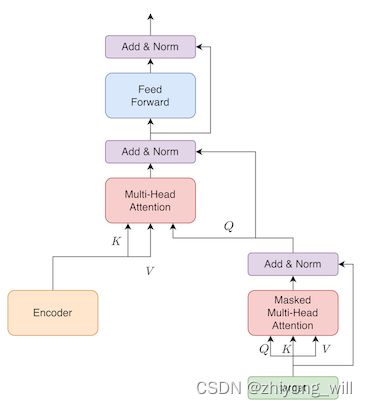
Transformer的基本原理
1. Seq2Seq框架
1.1. Seq2Seq框架概述
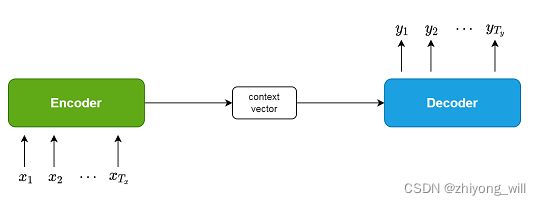
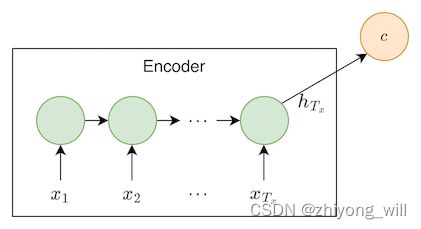
Seq2Seq[1]框架最初是在神经机器翻译(Neural Machine Translation,NMT)领域中提出,用于将一种语言(sequence)翻译成另一种语言(sequence)。其结构如下图所示:
在Seq2Seq框架中包含了Encoder和Decoder两个部分。在Encoder阶段,通过神经网络将原始的输入 { x 1 , x 2 , ⋯ , x T x } \left \{ x_1,x_2,\cdots,x_{T_x}\right \} {x1,x2,⋯,xTx}转换成固定长度的中间向量 { c 1 , c 2 , ⋯ , c l } \left \{ c_1,c_2,\cdots,c_l \right \} {c1,c2,⋯,cl},在Decoder阶段,将此中间向量作为输入,得到最终的输出 { y 1 , y 2 , ⋯ , y T y } \left \{ y_1,y_2,\cdots,y_{T_y} \right \} {y1,y2,⋯,yTy}。
1.2. 建模方法
在Encoder和Decoder部分,需要模型能够对时序数据建模,在NLP中,通常使用两种方式对时序数据建模,一种是以RNN[2],LSTM[3]为主的建模方法;另一种是以CNN[4],[5]为主的建模方法。
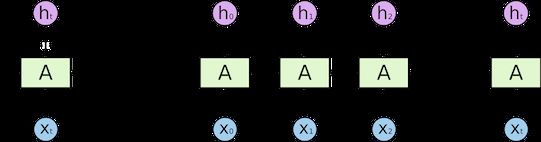
以RNN为例,其基本机构如下图所示:
在基于RNN的建模方法中, t t t时刻的状态更新依赖于 t − 1 t-1 t−1时刻的输出,即 t t t时刻的状态更新公式为:
h t = f ( U h t − 1 + W x t + b ) h_t=f\left ( Uh_{t-1}+Wx_t+b \right ) ht=f(Uht−1+Wxt+b)
在RNN的基础上衍生出很多优化的方案,如对于长距离依赖问题的优化,提出了LSTM以及GRU等模型;对于单向建模能力的问题,提出了双向的RNN模型,提升了对时序数据的建模能力。以简单的RNN为例,从上可以看出,RNN最大的问题是不容易并行化。因为 t t t时刻的状态更新依赖于 t − 1 t-1 t−1时刻的输出,所以必须先计算出 t − 1 t-1 t−1时刻的输出。
第二种是CNN的建模方法,以TextCNN[4],[5]模型为例:
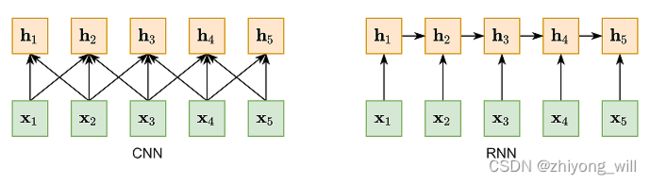
以最外层的红色为例,设置不同的filter的大小 N N N,如上图中filter的大小为2,通过filter的移动,可以计算filter内 N N N个词之间的相互依赖关系。与RNN相比,基于CNN的建模方法中,filter的计算是完全可以并行计算,是对RNN计算效率的极大提高。CNN与RNN对词的建模可以通过下图[6]进一步说明。
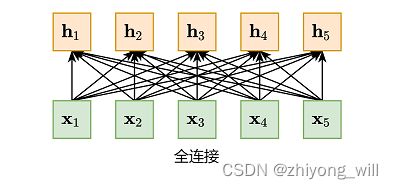
从图中可以看出,CNN和RNN都是对变长序列的一种“局部编码”:卷积神经网络是基于N-gram的局部编码;而对于循环神经网络,由于梯度消失等问题也只能建立短距离依赖。要解决这种短距离依赖的“局部编码”问题,建立输入序列之间的长距离依赖关系,可以使用以下两种方法:一种方法是增加网络的层数,通过一个深层网络来获取远距离的信息交互,另一种方法是使用全连接网络[6]。全连接网络如下图所示:
然而,全连接网络虽然可以对远距离依赖建模,但是无法处理变长的输入序列,同时,在全连接网络中,缺失了词之间的顺序信息。不同的输入长度,其连接权重的大小也是不同的。
综上,基于RNN,CNN以及全连接网络建模方法存在着以下的问题:
- 长距离依赖问题(RNN,CNN)
- 并行问题(RNN)
- 变长输入问题,词序信息问题(全连接网络)
1.3. Self-Attention
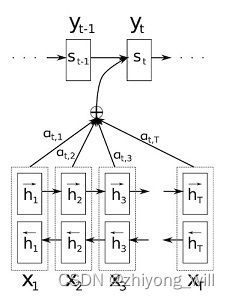
为了能提升Seq2Seq框架的性能,在Seq2Seq框架中引入了Attention机制[7],Attention机制通过对训练数据的学习,对其输入 x \mathbf{x} x的每一个特征赋予不同的权重,从而学习到对于目标更重要的信息,让模型具有更高的准确率。在Seq2Seq中引入Attention机制如下图所示:
其中,Attention的计算体现在针对不同的Decoder输出 y t y_t yt,都有一个对应的上下文向量 c t c_t ct, y t y_t yt的计算公式为:
y t = f ( y t − 1 , s t − 1 , c t ) y_t=f\left ( y_{t-1},s_{t-1},c_t \right ) yt=f(yt−1,st−1,ct)
其中, c t c_t ct为:
c i = ∑ j = 1 T x α i j h j c_i=\sum_{j=1}^{T_x}\alpha _{ij}h_j ci=j=1∑Txαijhj
其中, α i j \alpha _{ij} αij为归一化权重,其具体为:
α i j = e x p ( e i j ) ∑ k = 1 T x e x p ( e i k ) \alpha _{ij}=\frac{exp\left ( e_{ij} \right )}{\sum_{k=1}^{T_x}exp\left ( e_{ik} \right )} αij=∑k=1Txexp(eik)exp(eij)
其中, e i j e_{ij} eij表示的是第 i i i个输出前一个隐藏层状态 s i − 1 s_{i-1} si−1与第 j j j个输入隐层向量 h j h_j hj之间的相关性,可以通过一个MLP神经网络进行计算,即:
e i j = a ( s i − 1 , h j ) = v a T t a n h ( W a s i − 1 + U a h j ) e_{ij}=a\left ( s_{i-1},h_j \right )=v_a^Ttanh\left ( W_as_{i-1}+U_ah_j \right ) eij=a(si−1,hj)=vaTtanh(Wasi−1+Uahj)
上述的公式也表示了一般性的Attention的计算过程,即:
- 计算Attention得分: e i = a ( u , v i ) e_i=a\left ( \mathbf{u} ,\mathbf{v} _i \right ) ei=a(u,vi)
- 归一化: α i = e i ∑ i e i \alpha _i=\frac{e_i}{\sum_{i}e_i } αi=∑ieiei
- 输出: c = ∑ i α i v i c=\sum_{i} \alpha _i\mathbf{v} _i c=∑iαivi
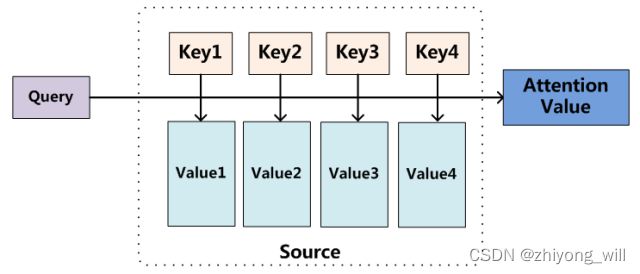
通常,一个Attention函数可以被描述成一个映射,其中该映射的输入是一个query和一组key-value对,其具体过程可以通过如下的图表示[8]:
与上式对应,Query为上式中的 u \mathbf{u} u,Key=Value为上式中的 v i \mathbf{v} _i vi。Self-Attention是一种特殊的Attention机制,即对于Query,为每一个 v i \mathbf{v} _i vi,即Query=Key=Value。以句子“The animal didn’t cross the street because it was too tired”[9]为例,计算Self-Attention的过程如下图所示:
以右侧的词为Query,Query与左侧的每一个Key计算Attention得分,从上图可以看出,Query(it_)与Key(animal_)的Attention得分比较大。Self-Attention的一般形式为: s o f t m a x ( X X T ) X softmax\left ( XX^T \right ) X softmax(XXT)X,Self-Attention的整个过程可由下图表示:
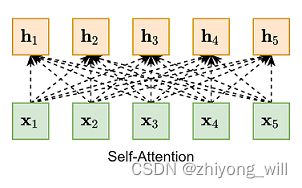
与上述全连接不同的是,Self-Attention不再受变长输入的影响。
1.3. Transformer概述
Self-Attention的提出解决了传统RNN模型的长距离依赖,不易并行的问题。虽然Self-Attention有这些优点,但是基本的Self-Attention本身并不能捕获词序信息,Google于2017年提出了解决Seq2Seq问题的Transformer模型[10],用Self-Attention的结构完全代替了传统的基于RNN的建模方法,同时在Transformer的模块中加入了词序的信息,最终在翻译任务上取得了比RNN更好的成绩。
在Transformer中依旧保留了Seq2Seq的Encoder+Decoder框架,在Encoder阶段对源文本编码,生成Embedding,记为 c c c,在Decoder阶段,综合已生成的文本与Encoder阶段的Embedding,已生成的文本记为 y 1 , y 2 , ⋯ , y t − 1 y_1,y_2,\cdots ,y_{t-1} y1,y2,⋯,yt−1,生成当前的词 y t y_t yt,即:
y t = f ( y t ∣ y 1 , y 2 , ⋯ , y t − 1 , c ) y_t=f\left ( y_t\mid y_1,y_2,\cdots ,y_{t-1},c \right ) yt=f(yt∣y1,y2,⋯,yt−1,c)
对于传统不带Attention的Seq2Seq框架中,Encoder阶段生成Embedding是固定不变的,如下图所示:
对于带有Attention的Seq2Seq框架中,Encoder阶段生成Embedding会根据当前需要预测的值计算一个动态的Embedding,具体如下图所示:
对于Transformer框架中的Encoder,会采用第二种方案。
2. 算法原理
Transformer的网络结构如下图所示:
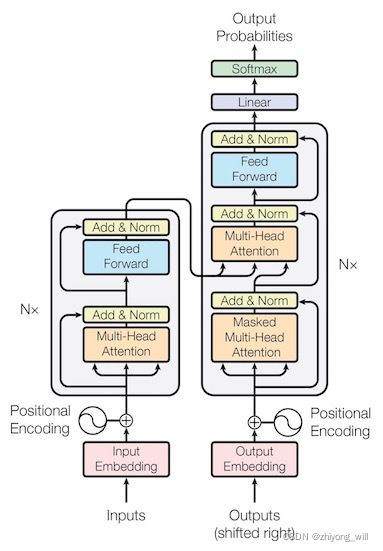
和大多数的Seq2Seq模型一样,在Transformer的结构中,同样是由Encoder(上图中的左侧部分)和Decoder(上图中的右侧部分)两个部分组成。以TensorFlow Core[11]的代码讲解为例子,帮助理解Transformer的整个结构。
2.1. Encoder
Encoder部分的结构如下图所示:
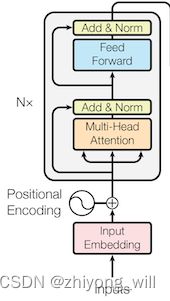
在Encoder部分,通过堆叠多个特定模块(如图中Nx部分),在文章[10]中,选择 N = 6 N=6 N=6。在该模块中,每个Layer由两个sub-layer组成,分别为Multi-Head Self-Attention和Feed Forward Network,在两个sub-layer中,都增加了残差连接和Layer Normalization操作,残差连接和Layer Normalization的作用是便于构建深层的网络,防止梯度弥散现象的出现。在参考文献[11]中的代码如下所示:
class Encoder(tf.keras.layers.Layer):
def __init__(self, num_layers, d_model, num_heads, dff, input_vocab_size,
maximum_position_encoding, rate=0.1):
super(Encoder, self).__init__()
self.d_model = d_model # 向量的维度
self.num_layers = num_layers # 编码层的层数,上图中的Nx部分
self.embedding = tf.keras.layers.Embedding(input_vocab_size, d_model) # 生成词向量
self.pos_encoding = positional_encoding(maximum_position_encoding,
self.d_model) # 生成位置编码
self.enc_layers = [EncoderLayer(d_model, num_heads, dff, rate)
for _ in range(num_layers)] # 每一个编码层函数
self.dropout = tf.keras.layers.Dropout(rate) # dropout
def call(self, x, training, mask):
seq_len = tf.shape(x)[1] # 文本长度
# 将嵌入和位置编码相加。
x = self.embedding(x) # (batch_size, input_seq_len, d_model) 词向量
x *= tf.math.sqrt(tf.cast(self.d_model, tf.float32)) # 参见下面注意点
x += self.pos_encoding[:, :seq_len, :] # 与位置编码相加
x = self.dropout(x, training=training) # dropout
for i in range(self.num_layers):
x = self.enc_layers[i](x, training, mask) # 每一个独立层的输出作为下一个独立层的输入
return x # (batch_size, input_seq_len, d_model)
注:在文献[10]中提到在Embedding层,乘以权重 d m o d e l \sqrt{d_{model}} dmodel。
2.1.1. 输入
在Transformer中摒弃了RNN的模型,使用基于Self-Attention模型,相比于RNN模型,基于Self-Attention的模型能够缓解长距离依赖以及并行的问题,然而,一般的Self-Attention模型中是无法对词序建模的,词序对于文本理解是尤为重要的,因此在文章[10]中,作者提到了两种位置编码(Positional Encoding)方法,然后将词的Embedding和位置的Embedding相加,作为最终的输入Embedding。两种位置编码分别为:
- 用不同频率的sin和cos函数计算
- 学习出Positional Embedding
通过经过实验发现两者的结果一样,最终作者选择了第一种方法:
P E ( p o s , 2 i ) = sin ( p o s / 100 0 2 i / d m o d e l ) PE_{\left ( pos,2i \right ) }=\sin \left ( pos/1000^{2i/d_{model}} \right ) PE(pos,2i)=sin(pos/10002i/dmodel)
P E ( p o s , 2 i + 1 ) = cos ( p o s / 100 0 2 i / d m o d e l ) PE_{\left ( pos,2i+1 \right ) }=\cos \left ( pos/1000^{2i/d_{model}} \right ) PE(pos,2i+1)=cos(pos/10002i/dmodel)
位置编码的代码在文献[11]中为:
def get_angles(pos, i, d_model): # 计算函数内的部分
angle_rates = 1 / np.power(10000, (2 * (i//2)) / np.float32(d_model))
return pos * angle_rates
def positional_encoding(position, d_model):
angle_rads = get_angles(np.arange(position)[:, np.newaxis],
np.arange(d_model)[np.newaxis, :],
d_model)
# 将 sin 应用于数组中的偶数索引(indices);2i
angle_rads[:, 0::2] = np.sin(angle_rads[:, 0::2])
# 将 cos 应用于数组中的奇数索引;2i+1
angle_rads[:, 1::2] = np.cos(angle_rads[:, 1::2])
pos_encoding = angle_rads[np.newaxis, ...] # 最终的位置编码向量
return tf.cast(pos_encoding, dtype=tf.float32)
通过原始词向量和位置向量相加,便得到了最终的带有位置信息的词向量。
2.2.2. Multi-Head Self-Attention
得到了词向量的序列后,假设为 X \mathrm{X} X,在Transformer中,通过线性变换分别得到 Q \mathrm{Q} Q, K \mathrm{K} K, V \mathrm{V} V,其计算过程如下图[9]所示:
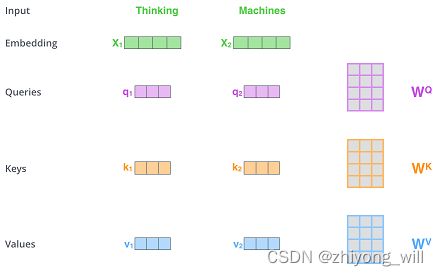
这里使用线性变换得到 Q \mathrm{Q} Q, K \mathrm{K} K, V \mathrm{V} V是为了进一步提升模型的拟合能力。
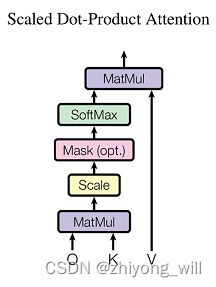
在Transformer中,使用的是Scaled Dot-Product Attention,其具体计算方法为:
A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q K T d k ) V Attention\left ( Q,K,V \right )=softmax\left ( \frac{QK^T}{\sqrt{d_k} }\right )V Attention(Q,K,V)=softmax(dkQKT)V
对于 1 d k \frac{1}{\sqrt{d_k} } dk1,其最主要的目的是对点积缩放。
引参考文献[11]:假设Q和K的均值为0,方差为1。它们的矩阵乘积将有均值为0,方差为 d k d_k dk,因此使用 d k d_k dk的平方根被用于缩放。因为Q和K的矩阵乘积的均值本应该为0,方差本应该为1,这样可以获得更平缓的softmax。当维度很大时,点积结果会很大,会导致softmax的梯度很小。为了减轻这个影响,对点积进行缩放。
计算过程可由下图表示:
Scaled Dot-Product Attention模块的代码在文献[11]中为:
def scaled_dot_product_attention(q, k, v, mask):
"""计算注意力权重。
q, k, v 必须具有匹配的前置维度。
k, v 必须有匹配的倒数第二个维度,例如:seq_len_k = seq_len_v。
虽然 mask 根据其类型(填充或前瞻)有不同的形状,
但是 mask 必须能进行广播转换以便求和。
参数:
q: 请求的形状 == (..., seq_len_q, depth)
k: 主键的形状 == (..., seq_len_k, depth)
v: 数值的形状 == (..., seq_len_v, depth_v)
mask: Float 张量,其形状能转换成
(..., seq_len_q, seq_len_k)。默认为None。
返回值:
输出,注意力权重
"""
matmul_qk = tf.matmul(q, k, transpose_b=True) # (..., seq_len_q, seq_len_k), Q*K^T
# 缩放 matmul_qk
dk = tf.cast(tf.shape(k)[-1], tf.float32) # 计算dk
scaled_attention_logits = matmul_qk / tf.math.sqrt(dk) # 缩放
# 将 mask 加入到缩放的张量上。
if mask is not None:
scaled_attention_logits += (mask * -1e9)
# softmax 在最后一个轴(seq_len_k)上归一化,因此分数
# 相加等于1。
attention_weights = tf.nn.softmax(scaled_attention_logits, axis=-1) # (..., seq_len_q, seq_len_k) # 归一化
output = tf.matmul(attention_weights, v) # (..., seq_len_q, depth_v) # 乘以V
return output, attention_weights
通过多个Scaled Dot-Product Attention模块的组合,就形成了Multi-Head Self-Attention,其过程如下图所示:
M u l t i H e a d ( Q , K , V ) = C o n c a t ( h e a d 1 , ⋯ , h e a d h ) W o MultiHead\left ( Q,K,V \right ) =Concat\left ( head_1,\cdots, head_h \right ) W^o MultiHead(Q,K,V)=Concat(head1,⋯,headh)Wo
其中,每一个 h e a d i head_i headi就是一个Scaled Dot-Product Attention。Multi-head Attention相当于多个不同的Scaled Dot-Product Attention的集成,引入Multi-head Attention可以扩大模型的表征能力,同时这里面的 h h h个Scaled Dot-Product Attention模块是可以并行的,没有层与层之间的依赖,相比于RNN,可以提升效率。
Multi-head Attention模块的代码在文献[11]中为:
class MultiHeadAttention(tf.keras.layers.Layer):
def __init__(self, d_model, num_heads):
super(MultiHeadAttention, self).__init__()
self.num_heads = num_heads # h的个数
self.d_model = d_model # 向量的维度
assert d_model % self.num_heads == 0
self.depth = d_model // self.num_heads
self.wq = tf.keras.layers.Dense(d_model) # 权重矩阵,用于和Q相乘
self.wk = tf.keras.layers.Dense(d_model) # 权重矩阵,用于和K相乘
self.wv = tf.keras.layers.Dense(d_model) # 权重矩阵,用于和V相乘
self.dense = tf.keras.layers.Dense(d_model) # 权重矩阵,用于最终输出
def split_heads(self, x, batch_size):
"""分拆最后一个维度到 (num_heads, depth).
转置结果使得形状为 (batch_size, num_heads, seq_len, depth)
"""
x = tf.reshape(x, (batch_size, -1, self.num_heads, self.depth))
return tf.transpose(x, perm=[0, 2, 1, 3])
def call(self, v, k, q, mask):
batch_size = tf.shape(q)[0]
q = self.wq(q) # (batch_size, seq_len, d_model)
k = self.wk(k) # (batch_size, seq_len, d_model)
v = self.wv(v) # (batch_size, seq_len, d_model)
q = self.split_heads(q, batch_size) # (batch_size, num_heads, seq_len_q, depth)
k = self.split_heads(k, batch_size) # (batch_size, num_heads, seq_len_k, depth)
v = self.split_heads(v, batch_size) # (batch_size, num_heads, seq_len_v, depth)
# scaled_attention.shape == (batch_size, num_heads, seq_len_q, depth)
# attention_weights.shape == (batch_size, num_heads, seq_len_q, seq_len_k)
scaled_attention, attention_weights = scaled_dot_product_attention(
q, k, v, mask) # 计算Scaled dot product attention
scaled_attention = tf.transpose(scaled_attention, perm=[0, 2, 1, 3]) # (batch_size, seq_len_q, num_heads, depth)
# 将多个scaled attention通过concat连接在一起
concat_attention = tf.reshape(scaled_attention,
(batch_size, -1, self.d_model)) # (batch_size, seq_len_q, d_model)
output = self.dense(concat_attention) # (batch_size, seq_len_q, d_model) # 得到最终的输出
return output, attention_weights
2.2.3. Layer Normalization
Layer Normalization是针对每条样本进行归一化,可以对Transformer学习过程中由于Embedding累加可能带来的“尺度”问题加以约束,相当于对表达每个词一词多义的空间加以约束,有效降低模型方差。在TF中可以使用tf.keras.layers.LayerNormalization()函数直接实现Layer Normalization功能。在Transformer中,Layer Normalization是对残差连接后的结果进行归一化,具体公式如下所示:
L a y e r N o r m ( x + S u b l a y e r ( x ) ) LayerNorm\left ( x+Sublayer\left ( x \right ) \right ) LayerNorm(x+Sublayer(x))
2.2.4. Position-wise FFN
Position-wise Feed Forward Network就是一个全连接网络,在Transformer中,这个部分包含了两个FFN网络,可以由下述的公式表示:
F F N ( x ) = max ( 0 , x W 1 + b 1 ) W 2 + b 2 FFN\left ( x \right )=\max \left ( 0, xW_1+b_1 \right ) W_2+b_2 FFN(x)=max(0,xW1+b1)W2+b2
Position-wise FFN模块的代码在文献[11]中为:
def point_wise_feed_forward_network(d_model, dff):
return tf.keras.Sequential([
tf.keras.layers.Dense(dff, activation='relu'), # (batch_size, seq_len, dff) # 全联接1,激活函数为relu
tf.keras.layers.Dense(d_model) # (batch_size, seq_len, d_model) # 全联接2
])
组合上述的多个部分,最终形成了Encoder模块部分,其代码在文献[11]中为:
class EncoderLayer(tf.keras.layers.Layer):
def __init__(self, d_model, num_heads, dff, rate=0.1):
super(EncoderLayer, self).__init__()
self.mha = MultiHeadAttention(d_model, num_heads) # 多头Attention
self.ffn = point_wise_feed_forward_network(d_model, dff) # position-wise FFN
self.layernorm1 = tf.keras.layers.LayerNormalization(epsilon=1e-6) # layer-normalization
self.layernorm2 = tf.keras.layers.LayerNormalization(epsilon=1e-6) # layer-normalization
self.dropout1 = tf.keras.layers.Dropout(rate) # dropout
self.dropout2 = tf.keras.layers.Dropout(rate) # dropout
def call(self, x, training, mask):
attn_output, _ = self.mha(x, x, x, mask) # (batch_size, input_seq_len, d_model) 计算Attention
attn_output = self.dropout1(attn_output, training=training) # 对结果dropout
out1 = self.layernorm1(x + attn_output) # (batch_size, input_seq_len, d_model) # 残差连接+layer-normalization
ffn_output = self.ffn(out1) # (batch_size, input_seq_len, d_model) position-wise FFN
ffn_output = self.dropout2(ffn_output, training=training) # 对结果dropout
out2 = self.layernorm2(out1 + ffn_output) # (batch_size, input_seq_len, d_model) # 残差连接+layer-normalization
return out2
2.2. Decoder
Decoder部分的结构如下图所示:

在Decoder部分,通过堆叠多个特定模块(如图中Nx部分),在文章[10]中,选择 N = 6 N=6 N=6。在该模块中,每个Layer由三个sub-layer组成,分别为Masked Multi-Head Self-Attention,Multi-Head Self-Attention和Feed Forward Network,与Encoder中的sub-layer一样,每个sub-layer都增加了残差连接和Layer Normalization操作。与Encoder中不一样的地方主要有两个:
- 增加了Masked Multi-Head Self-Attention这个sub-layer
- Multi-Head Self-Attention的输入不一样,在Encoder中, Q Q Q, K K K和 V V V的值都是一样的,而在Decoder中的 Q Q Q的值来自本身的输入向量,而 K K K和 V V V则来自于Encoder的输出
Decoder部分的代码在参考文献[11]中如下所示:
class Decoder(tf.keras.layers.Layer):
def __init__(self, num_layers, d_model, num_heads, dff, target_vocab_size,
maximum_position_encoding, rate=0.1):
super(Decoder, self).__init__()
self.d_model = d_model # 向量维度
self.num_layers = num_layers # 解码器的层数,上图中的Nx
self.embedding = tf.keras.layers.Embedding(target_vocab_size, d_model) # 输入的词映射成Embedding
self.pos_encoding = positional_encoding(maximum_position_encoding, d_model) # 输入词的位置编码
self.dec_layers = [DecoderLayer(d_model, num_heads, dff, rate)
for _ in range(num_layers)] # 解码层
self.dropout = tf.keras.layers.Dropout(rate) # dropout
def call(self, x, enc_output, training,
look_ahead_mask, padding_mask):
seq_len = tf.shape(x)[1] # 输入句子长度
attention_weights = {}
x = self.embedding(x) # (batch_size, target_seq_len, d_model) # 输入词向量
x *= tf.math.sqrt(tf.cast(self.d_model, tf.float32)) # 同encoder的输入操作
x += self.pos_encoding[:, :seq_len, :] # 与位置编码相加
x = self.dropout(x, training=training) # dropout
for i in range(self.num_layers): # 解码层
x, block1, block2 = self.dec_layers[i](x, enc_output, training,
look_ahead_mask, padding_mask)
attention_weights['decoder_layer{}_block1'.format(i+1)] = block1
attention_weights['decoder_layer{}_block2'.format(i+1)] = block2
# x.shape == (batch_size, target_seq_len, d_model)
return x, attention_weights
最终,在Encoder阶段,会针对输入中的每一个词产出一个Embedding表示,正如上述代码中的x的大小为[target_seq_len, d_model]。
2.2.1. Decoder部分的输入
Decoder部分的作用是在 t t t时刻,根据上下文信息(即Encoder中对源文本的编码信息)以及 t t t时刻之前已生成好的文本,得到当前 t t t时刻的输出,因此,在Decoder模块中,输入分为两个部分,一部分是Encoder部分的输出,一部分是Seq2Seq的目标Seq的Embedding,其中源Seq的Embedding输入到Encoder中。对于Seq的处理与Encoder中一致,详细为:
x = self.embedding(x) # (batch_size, target_seq_len, d_model) # 输入词向量
x *= tf.math.sqrt(tf.cast(self.d_model, tf.float32)) # 同encoder的输入操作
x += self.pos_encoding[:, :seq_len, :] # 与位置编码相加
2.2.2. Masked Multi-Head Self-Attention
Masked是Transformer中很重要的概念,其实在Transformer中存在两种Mask。Mask的含义是掩码,它能掩藏某些值,使得模型在参数更新时对模型掩藏。Transformer中包含了两种Mask,分别是padding mask和sequence mask。其中,padding mask在所有的Scaled Dot-Product Attention里面都需要用到,而sequence mask只有在Decoder的Masked Multi-Head Self-Attention里面用到。
Masked Language Model:即对文本中随机掩盖(mask)部分词,并通过训练语言模型,将masked掉的词填充好,以此训练语言模型。
- padding mask
对于输入序列都要进行padding补齐,也就是说设定一个统一的句子长度 N N N,对于橘子长度不满 N N N的序列后面填充 0 0 0,如果输入的序列长度大于 N N N,则截取左边长度为 N N N的内容,把多余的直接舍弃。对于padding补齐,对于填充值 0 0 0的位置,最终在该位置mask输出为 1 1 1,否则输出为 0 0 0。在参考文献[11]中代码为:
def create_padding_mask(seq):
seq = tf.cast(tf.math.equal(seq, 0), tf.float32) # 填充0
# 添加额外的维度来将填充加到
# 注意力对数(logits)。
return seq[:, tf.newaxis, tf.newaxis, :] # (batch_size, 1, 1, seq_len)
在Self-Attention的计算过程中,对于mask为 1 1 1的位置,具体的做法是,把这些位置的值加上一个非常大的负数,这样经过Softmax后,这些位置的权重就会接近 0 0 0,具体如scaled_dot_product_attention函数中所示:
# 将 mask 加入到缩放的张量上。
if mask is not None:
scaled_attention_logits += (mask * -1e9)
- sequence mask
sequence mask是为了使Decoder模块不能看见未来的信息。在Decoder模块中,希望在 t t t时刻,只利用Encoder的输出以及 t t t时刻之前的输出,而需要对 t t t时刻以及 t t t时刻之后的信息隐藏起来。具体做法就是产生一个上三角矩阵,上三角的值全为 0 0 0,把这个矩阵作用在每一个序列上。在参考文献[11]中代码为:
def create_look_ahead_mask(size):
mask = 1 - tf.linalg.band_part(tf.ones((size, size)), -1, 0)
return mask # (seq_len, seq_len)
两个部分的mask组合在一起,在参考文献[11]中的代码如下所示:
def create_masks(inp, tar):
# 编码器填充遮挡
enc_padding_mask = create_padding_mask(inp) # 编码器的padding
# 在解码器的第二个注意力模块使用。
# 该填充遮挡用于遮挡编码器的输出。
dec_padding_mask = create_padding_mask(inp) # 解码器的padding
# 在解码器的第一个注意力模块使用。
# 用于填充(pad)和遮挡(mask)解码器获取到的输入的后续标记(future tokens)。
look_ahead_mask = create_look_ahead_mask(tf.shape(tar)[1]) # 编码器的mask
dec_target_padding_mask = create_padding_mask(tar) # 解码器对target做padding
combined_mask = tf.maximum(dec_target_padding_mask, look_ahead_mask) # mask
return enc_padding_mask, combined_mask, dec_padding_mask
2.2.3. Decoder的核心部分
对于Decoder的核心部分,包含了 N x Nx Nx组的多种Attention的堆叠,对于每一组的结构如下图所示:
对于Masked Multi-Head Attention,其输入为target的Embedding与Position Embedding的和,其输出作为Multi-Head Attention的输入 Q Q Q,而Multi-Head Attention的输入 K K K和 V V V则是来自于Encoder的输出。Decoder阶段与Encoder阶段的不同的是,在Encoder阶段可以做并行计算,但是在Decoder阶段,需要根据 t t t时刻前面的输出预测 t t t时刻的值,而 t t t时刻前面的输出即为Masked Multi-Head Attention的输入。Decoder过程在参考文献[11]中的代码如下所示:
class DecoderLayer(tf.keras.layers.Layer):
def __init__(self, d_model, num_heads, dff, rate=0.1):
super(DecoderLayer, self).__init__()
self.mha1 = MultiHeadAttention(d_model, num_heads)
self.mha2 = MultiHeadAttention(d_model, num_heads)
self.ffn = point_wise_feed_forward_network(d_model, dff)
self.layernorm1 = tf.keras.layers.LayerNormalization(epsilon=1e-6)
self.layernorm2 = tf.keras.layers.LayerNormalization(epsilon=1e-6)
self.layernorm3 = tf.keras.layers.LayerNormalization(epsilon=1e-6)
self.dropout1 = tf.keras.layers.Dropout(rate)
self.dropout2 = tf.keras.layers.Dropout(rate)
self.dropout3 = tf.keras.layers.Dropout(rate)
def call(self, x, enc_output, training,
look_ahead_mask, padding_mask):
# enc_output.shape == (batch_size, input_seq_len, d_model)
attn1, attn_weights_block1 = self.mha1(x, x, x, look_ahead_mask) # (batch_size, target_seq_len, d_model) # Decoder部分的输入,经过第一个Masked Multi-Head Attention
attn1 = self.dropout1(attn1, training=training) # dropout
out1 = self.layernorm1(attn1 + x) # layer normalization和残差连接
attn2, attn_weights_block2 = self.mha2(
enc_output, enc_output, out1, padding_mask) # (batch_size, target_seq_len, d_model) # 第二个Multi-Head Attention
attn2 = self.dropout2(attn2, training=training) # dropout
out2 = self.layernorm2(attn2 + out1) # (batch_size, target_seq_len, d_model) # layer normalization和残差连接
ffn_output = self.ffn(out2) # (batch_size, target_seq_len, d_model) # 全连接
ffn_output = self.dropout3(ffn_output, training=training) # dropout
out3 = self.layernorm3(ffn_output + out2) # (batch_size, target_seq_len, d_model) # layer normalization和残差连接
return out3, attn_weights_block1, attn_weights_block2
2.3. 模型训练
有了上述的Encoder和Decoder模块,对于一个完整的Seq2Seq框架,需要综合这两个部分的逻辑,完整的Transformer的代码在参考文献[11]为:
class Transformer(tf.keras.Model):
def __init__(self, num_layers, d_model, num_heads, dff, input_vocab_size,
target_vocab_size, pe_input, pe_target, rate=0.1):
super(Transformer, self).__init__()
self.encoder = Encoder(num_layers, d_model, num_heads, dff,
input_vocab_size, pe_input, rate) # Encoder模块
self.decoder = Decoder(num_layers, d_model, num_heads, dff,
target_vocab_size, pe_target, rate) # Decoder模块
self.final_layer = tf.keras.layers.Dense(target_vocab_size) # 最后的全连接层
def call(self, inp, tar, training, enc_padding_mask,
look_ahead_mask, dec_padding_mask):
enc_output = self.encoder(inp, training, enc_padding_mask) # (batch_size, inp_seq_len, d_model) # Encoder模块的输出
# dec_output.shape == (batch_size, tar_seq_len, d_model)
dec_output, attention_weights = self.decoder(
tar, enc_output, training, look_ahead_mask, dec_padding_mask) # Decoder模块的输出
final_output = self.final_layer(dec_output) # (batch_size, tar_seq_len, target_vocab_size) # 全连接输出
return final_output, attention_weights
3. 总结
Transformer对基于递归神经网络RNN的Seq2Seq模型的巨大改进。在文本序列的学习中能够更好的提取文本中的信息,在Seq2Seq的任务中取得较好的结果。但Transformer自身也存在一定的局限性,最主要的是注意力只能处理固定长度的文本字符串,这对于长文本来说会丢失很多信息。
参考文献
[1] Cho K, Merrienboer B V, Gulcehre C, et al. Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation[J]. Computer Science, 2014.
[2] 循环神经网络RNN
[3] 长短期记忆网络LSTM
[4] CNN在文本建模中的应用TextCNN
[5] Y. Kim, “Convolutional neural networks for sentence classification,” in Proceedings of EMNLP 2014
[6] 神经网络与深度学习
[7] Bahdanau D, Cho K, Bengio Y. Neural machine translation by jointly learning to align and translate[J]. arXiv preprint arXiv:1409.0473, 2014.
[8] Attention注意力机制与self-attention自注意力机制
[9] The Illustrated Transformer
[10] Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need[J]. Advances in neural information processing systems, 2017, 30.
[11] 理解语言的 Transformer 模型
[11] transformer面试题的简单回答
[12] nlp中的Attention注意力机制+Transformer详解
[13] 深度学习中的注意力模型(2017版)
[14] Jimmy Lei Ba, Jamie Ryan Kiros, and Geoffrey E Hinton. Layer normalization. arXiv preprint arXiv:1607.06450, 2016.
[15] 模型优化之Layer Normalization
[16] 超详细图解Self-Attention
[17] 【经典精读】Transformer模型和Attention机制
[18] Transformer解析与tensorflow代码解读