词典及容错处理
在前面几篇文章中都是在讲倒排索引的结构, 及合并优化方法. 这篇博文里更多谈下怎么根据输输入查询参数来定位到倒排记录表的指针. 其实这跟MySQL中对VARCHAR类型加索引后, 然后基于该字段查询的原理一样, 都是可以基于B-Tree的经典数据结构来快速定位. MySQL中基于内存表还可以用hash索引, 同样信息检索技术中也可以用这种方式, 但是基于hash函数的有个缺点是它不能进行前缀模糊查询, 比如查询hell*, 以hell开头的关键字. 原因很简单, 因为凡是两个关键字只要有一点不同, 最终通过哈希计算后的结果都可以是截然不同的. 所以用得最多的还是基于树的结构. 关于B-Tree的数据结构及操作算法, 可以google到很多介绍文章, 就不说了. 这里讨论下两个问题: 一是通配符查询, 我们前面说过前缀查询比较简单, 但是如果通配符不在结尾, 比如he*o, 或者*red, 这在B-Tree里是无法做直接做到的. 第二个问题: 我们经常搜索查询词时拼写错误, 比如我就经常在google中搜索lucene但是却打入的lucence, 这时候google会自动识别我是否想真正想要查询的是lucene, 这就是拼写校正技术. 下面详细讨论这两点.
通配符查询(general wildcard queries)
我们在基于数据库(MySQL)的应用开发时, 对于字段的模糊查询, 我们一般建议产品需求是只能满足前缀查询, 如trian*, 如果需求非要做到也能后缀查询, 如*orgal, 这时候我们一般会在表中冗余一个字段, 此字段是对原字段按照完全相反的字符展示顺序存储, 比如原字段中存储的是hello, 那么冗余字段中存储的就是olleh, 这样用户如果是前缀模糊查询就按原字段比较查询, 如果是后缀查询, 就按冗余的字段查询. 而在信息检索中一样可以这样来做, 我们的词典完全可以冗余一个反序的词典表, 专门用来做后缀查询. 这时聪明的你肯定会想到, 对于通配符在中间的查询的做法, 如查询dic*ary, 我们可以通过前缀查询dic*和后缀查询yra*, 然后取交集, 就是我们所想满足的所有词. 这种基于两个B树结构的交集运算, 就像MySQL中的索引合并(Index Merge)一样.
轮排索引(Permuterm Indexes)
什么叫轮排, 举个例子, 如果对于词项hello来说, 我们会同时生成hello$, ello$h, llo$he, lo$hel, o$hell, 它们都指向原始词项hello. 这样假如我们现在要查询he*o时, 我们只要在该查询关键字后面加上$然后旋转到*出现在最后面, 得到o$he*, 然后在轮排词典中前缀查询, 就可以查询得到到所以对应的原始词项, 继而可以根据这些词项定位到倒排记录表的指针.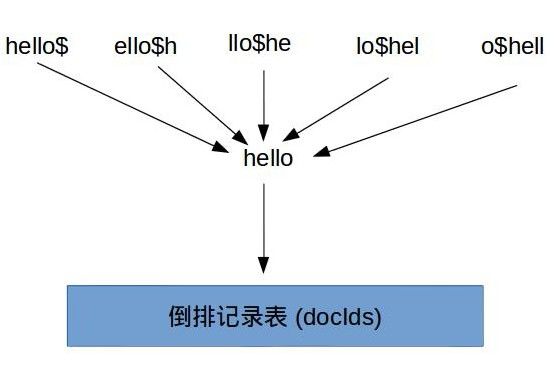
K-gram索引
轮排索引的缺点显而易见, 就是会使轮排词典变得很大. 就像上面举的例子, 如果一个词项由n的字母组成, 通过旋转会产生n个词项. 这种存储增长很恐怖的. k-gram索引的原理很简单, 这里面的k是代表数量, 可是是2, 也可以是3. 比如hello会被拆解成$he, hel, ell, llo, lo$. 这样我们如果查询he*lo, 只要在分解后的K-gram记典中找$he和lo$对应的原始词项, 并定位到它们的倒排记录表进行相交运算即可.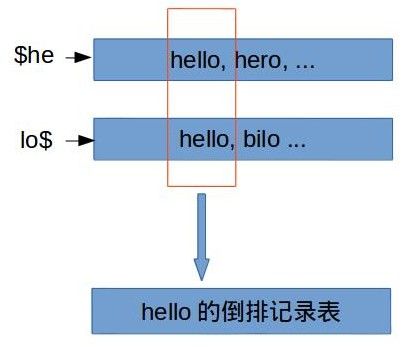
K-gram相比倒排索引, 虽然一个词项也会产生多个辅助词项, 但是因为k的粒度问题, 使每个gram的重用率很高.
这里要注意的是, 无论是轮排索引, 还是K-gram索引, 查找出来的原始词项都有可能不是我们想要的词项. 但是我们可以通过初步筛选出来的词项集合(数量很少)再次做进一步的筛选.
拼写较正(Spelling Collection)
我们在输入查询词, 经常不确定或者记错, 导致输入和实际想要的看起来相似, 但是又是错误的, 比如:
这里用到的技术就是要计算两个词的相异程度, 专业的术语叫做编辑距离(edit distance). 编辑距离最早由俄罗斯科学家Levenshtein于1965年提出, 具体的算法则是1974由Wagner和Fischer提出. 这里我们来详细讨论下.
两个单词s1, s2的差距, 可以这样来理解: 把s1变成s2要经过多少步骤. 比如把"kitten" 变成"sitting", 要经过下面三步:
- kitten -> sitten (把k替换成s)
- sitten -> sittin (把e替换成i)
- sittin -> sitting (在后面加上g)
所以kitten和sitting的编辑距离是3. 这里用python写出这个核心算法:
def edit_distance(s1, s2):
m = len(s1)
n = len(s2)
d = [[0 for j in range(n + 1)] for i in range(m + 1)] # 先初始化一个二维数据, d[i][j]表示s1的前i个字符组成的字符串和s2前j个字符组成的字符串的编辑距离
for i in range(m + 1): # 初始化d[i][0]为i. 这点很容易理解, s1的第i个字符转变成空白字符串(j=0), 只要去掉i个字符就可以了, 所以操作数是i
d[i][0] = i
for j in range(n + 1): # 初始化d[0][j]为j, 和上面一样, s2第j个字符之前组成的串变成空白字符串(i=0), 只要去掉j个字符就可以了, 所以操作数是j
d[0][j] = j
for i in range(m):
for j in range(n):
if s1[i] == s2[j]: # 如果s1的第i的字符等于s2的第j个字符, 那么这一步操作就不用做, 所以编辑距离就是s1的第i-1个字符和s2的第j-1个字符的编辑距离
d[i+1][j+1] = d[i][j]
else:
d[i+1][j+1] = min(d[i][j+1] + 1, d[i+1][j] + 1, d[i][j] + 1) # 在基于前面一步的基础上, 把s1删除一个字符, 或者把s2插入一个字符, 或者把s2的第j个字符替换成s1的第i个字符
print 'the edit distance is %s' % d[m][n]