轻量级神经网络算法系列文章-ShuffleNet v2

4. 轻量级神经网络算法目录

4. 轻量级神经网络算法
   4.1 各轻量级神经网络算法总结对比
   4.2 SqueezeNet
   4.3 DenseNet
   4.4 Xception
   4.5 MobileNet v1
   4.6 IGCV
   4.7 NASNet
   4.8 CondenseNet
   4.9 PNASNet
   4.10 SENet
   4.11 ShuffleNet v1
   4.12 MobileNet v2
   4.13 AmoebaNet
   4.14 IGCV2
   4.15 IGCV3
   4.16 ShuffleNet v2
   4.17 MnasNet
   4.18 MobileNet v3

---

深度学习知识点总结

专栏链接:
https://blog.csdn.net/qq_39707285/article/details/124005405
本专栏主要总结深度学习中的知识点，从各大数据集比赛开始，介绍历年冠军算法；同时总结深度学习中重要的知识点，包括损失函数、优化器、各种经典算法、各种算法的优化策略Bag of Freebies (BoF)等。

---

---

4.16 ShuffleNet v2

4.16.1 现存的问题

目前，神经网络的结构设计只依靠FLOPs来评估网络复杂度。但是，FLOPs是一个近似值，通常不等同于我们真正关心的直接度量，例如速度或延迟。另外，影响网络性能还有其他很重要的因素，例如内存消耗、应用平台的性能(例如硬件)等，同一个网络结构在不同的应用平台上差异还是挺大的。

4.16.2 问题分析

实际上，我们更直看网络结构的效率是通过速度来判断的，速度是网络结构效率的直接度量，FLOPs是间接度量。 那为什么FLOPs并不能完全决定速度呢？

直接度量（速度）和间接度量（FLOPs）之间的差异可归因于两个主要原因：

1. FLOPs未考虑 内存访问成本（MAC,memory access cost）
   注意：这里的MAC不是MACs(Multiply–Accumulate Operations:乘加累积操作数)
   MAC对速度有相当大的影响。在某些操作（如组卷积）中，这种成本占运行时间的很大一部分。这可能是具有强大计算能力的设备（如GPU）的瓶颈。在网络架构设计期间，不能忽略此成本。
2. 另外一个是 并行度(degree of parallelism)
   在相同的FLOPs下，具有高并行度的模型比具有低并行度的模型快得多。由于平台(硬件)的不同，相同FLOPs的操作可能具有不同的运行时间。现在有好多算法采用张量分解来减少FLOPs以加速矩阵乘法，但是也有研究表明，即使张量分解节省了75%的FLOPs，但是在GPU上依然运算很慢。调查分析这个问题之后，发现这是因为最新的CUDNN库专门针对3×3 conv进行了优化，对其他卷积例如(1×1组卷积等)优化不够。所以3×3卷积比1×1卷积的FLOPs大了9倍，但是3×3卷积的速度并没有比1×1慢9倍。

小结：只使用FLOPs值来判断网络的效率是不够的。例如相同FLOPs不同网络结构的运算耗时可能不同，即使是相同FLOPs和相同的网络结果在不同的硬件平台上运算耗时也可能不同。所以还需要考虑 内存访问成本(MAC)和并行度(degree of parallelism)

根据这些特点，可以发现有效的网络架构设计应考虑以下两个原则：

1. 应使用直接度量（如速度），而不是间接度量（FLOPs）
2. 应该直接在目标平台上评估网络的性能

本文遵循这两个原则，提出了一种更有效的网络架构ShuffleNet v2，另外在一系列实验的基础上，还提出了能有效进行网络设计的几个实用指南（G1/G2/G3/G4详见3-6小节），这些指南与应用平台无关，无论是在GPU还是ARM平台上都可以使用。

4.16.3 G1:相等的输入输出通道宽度使MAC最小化

目前好多网络设计都使用深度可分离卷积，其中的逐点卷积(PW，1×1卷积)占用了大量的复杂度。1×1卷积核主要由输入通道数c1和输出通道数c2决定，假设计算设备中的缓存足够大以存储整个特征映射和参数，记输入特征图的宽和高分别是w和h，则1×1卷积的FLOPs为：

FLOPs：B=h×w×c1×c2
MAC：MAC=h×w×(c1+c2)+c1×c2

根据均值不等式，得出：
MAC $\ge$ 2$\sqrt{hwB}$+$\frac{B}{hw}$

可以看出，MAC可以由FLOPs得到下限，当输入和输出通道的数量相等时，它达到下限，即当c1=c2时，MAC值最小，速度应该也最快。

但这些也都是理论上，实际上，许多设备上的缓存不够大。因此，实际MAC可能会偏离理论MAC。所有为了验证上述理论结论，进行了如下实验，通过重复堆叠10个blocks来构建基准网络，每个block包含两个卷积层。共进行四个实验，每个实验都通过改变通道的数量来固定的FLOPs，实验结果如下表：

显然， 当c1:c2接近1:1时，MAC变得更小，网络预测速度更快。即输入输出通道数相等时，速度最快。

4.16.4 G2:过多的组卷积会增加MAC

组卷积是现在好多网络设计的核心，它通过减少信道数量来降低计算复杂度（FLOPs）。一方面，它允许在给定固定FLOPs的情况下使用更多通道，并增加网络表达信息的能力（从而提高精度）。但是，另一方面，通道数量的增加导致更多的MAC。
例如1×1组卷积的MAC如下(其中g是组卷积的分组数)：
$FLOP=B=hw{c}_1{c}_2/g$
$MAC=$$hw(c_1+c_2)+$$\frac{c_1{c}_2}{g}$=$hw{c}_1+$$\frac{Bg}{c_1}$+$\frac{B}{hw}$

可以看出，输入c1×h×w固定，MAC随着g的增大而增大。

为了研究实际中的影响，通过堆叠10个逐点组卷积层(1×1组卷积)来构建基准网络。下表展示了在固定FLOPs的情况下，使用不同组数的组卷积的速度影响，

显然，使用大的组数会显著降低运行速度，例如，使用8个组数的在GPU上比使用1个组数的慢两倍多，在ARM上慢30%。这主要是因为MAC增加了。

因此，本文认为要根据目标平台和任务仔细选择组卷积的组数，简单地使用大组数是不明智的，因为这可能会使用更多的通道数。快速增加的计算成本很容易超过精度提高带来的好处。

4.16.5 G3:网络碎片降低了并行度

GoogLeNet系列和其他利用神经网络搜素生成的网络，例如NasNET,MansNet等，广泛采用”multi_path”，如下图所示(前两张是inception中的，第三张是NASNet-A)：



里面包含很多小的运算结构（称之为碎片化运算，每个卷积和池化运算都可以看出一个小碎片运算）的运算，例如NasNet-A中，碎片运算的数量（即一个block中的单个卷积或pool运算的数量）为13，而ResNet中式2或者3。

即使这些碎片结构可以提高准确率，但同样会减少效率，因为它对强并行的设备不友好，例如GPU等计算能力，它还引入了额外的开销，例如内核的启动和同步。

为了量化网络碎片如何影响效率，本文评估了一系列具有不同碎片程度的网络block，每个block由1到4个1×1卷积组成，它们按顺序或并行排列，示意图如下，每个block重复堆叠10次。

实验结果如表3所示：

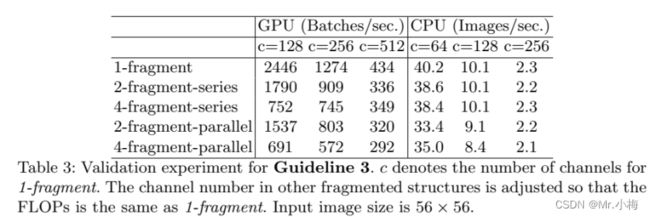
从表中可以看出，碎片化显著降低了GPU上的速度，例如4-fragment structure 比1-fragment慢3倍，在ARM上，速度降低相对较小。
因此，减少碎片化操作能有效提升网络速度。

4.16.6 G4:Element-wise运算增加时间成本

在轻量级网络如MobileNet和ShuffleNet v1中，element-wise运算耗费了大量的时间，尤其是在GPU上耗时占用更多，具体如下图所示：

这些运算包括Relu/AddTensor/AddBias等等，它们FLOPs很小，但MAC相对很大，拿深度可分离卷积来说，它有很大的MAC/FLOPs比。

接着进行实验验证，使用ResNet的bottleneck unit(1×1conv -> 3×3conv -> 1×1conv)，去除其中的ReLU和shortcut连接，如下表4中展示了不同变体的运行时间：

从表中可以观察到，在删除ReLU和short_cut后，GPU和ARM上都获得了大约20%的加速。

因此，过多的Element-wise运算(例如ReLU、short-cut等)会增加时间消耗。

4.16.7 小结

综合G1/G2/G3/G4的分析，可以得出结论，一个有效的网络架构应该有：

1.使用”balanced” conv，相同的输入输出通道数

2.注意组卷积会增加的成本消耗

3.减少碎片化程度(例如并行或串联的卷积、池化等)

4.减少element-wise运算(例如ReLU/AddTensor/AddBias)

最近的轻量级神经网络算法并没有考虑这些因素，例如ShuffleNet v1中，有大量的组卷积（违反了G2），还有大量的bottleneck类似的block（违反了G1），MobileNet v2中有inverted bottleneck structure违反了G1，使用了深度可分离卷积和ReLU，违反了G4。神经网络搜索自动生成的网络（例如NASNet）重度使用碎片化运算，违反G3。

4.16.7 网络结构设计

本文引入了一个简单的运算符，称为通道分割(channel split，如图3(c)所示。在每个单元的开始，把c维的输入特征分割成两个分支，一个$c^{‘}$维，一个c-c`维。 根据G3，一个分支直接连接，另外一个分支由3个卷积组成；根据G1，设置每个卷积的输入输出通道数一样；根据G2，1×1卷积不再使用组卷积，还有一个原因是拆分操作已经产生了两个组，不用再分组卷积了。

卷积之后的结果，和直接连接的分支concat起来，所以总体输入输出通道数依然相等（遵守了G1），同样使用ShuffleNet v1中的channel shuffle，用于实现两个分支之间的信息通信，如图3(c)(d)。在channel shuffle之后，接着新的一个unit开始。ShuffleNet V1中的Add运算不再使用，Element-wise运算（ReLU，深度卷积）只在一个branch中使用，“concat”、“channel shuffle”和“channel split”合并成一个运算（根据G4）。

下采样处理时，具体网络结构如图3(d)所示，channel split移除，因此，输出通道数增倍，特征图宽高减倍。

以上图中的(c)(d)即ShuffleNet v2的全部单元结构，基于以上分析，这种架构设计是高效的，因为它遵循了所有的准则。

使用block(c)(d)重复堆叠以构建整个网络，为了简单起见，channel split中的c`=c/2，网络结构如下表所示，与ShuffleNet v1一样，每个block中的通道数量可以被缩放以生成不同复杂度的网络，标记为0.5×、1×，等等。

4.16.8 总结

1. 仅仅使用FLOPs来判断网络的速度是不够的，影响速度的还有两个主要因素： 内存访问成本(MAC)和并行度(degree of parallelism)
   
2. 通过对影响因素MAC和并行度的分析，提供了4个实用指南
3. G1：相等的输入输出通道宽度可以使MAC最小化
   
4. G2：过多的组卷积会增加MAC
   
5. G3：网络碎片降低了并行度
   
6. G4：Element-wise运算增加时间成本
   
7. 以ShuffleNet v1为基准，根据4个指南对网络进行修改：
8. 根据G1：设置每个block的输入输出通道数一样(stride=2的block除外)；
   
9. 根据G2：1×1卷积不再使用组卷积；
   
10. 根据G3： 使用channel split把输入特征分成两个分支，一个分支直接连接，另外一个分支由3个卷积组成；
    
11. 根据G4：张量之间不再使用Add运算，改成concat，另外把concat、channel shuffle和channel split合并成一个运算