SGU 156. Strange Graph（欧拉路）

时间限制：0.25s

空间限制：6M

题目描述

       让我们想象一个无向图G=<V，E>.如果边（u，v）在边集E中，那么我们就说两个顶点u和v是邻接点.在这种情况下，我们也说u是v的一个邻接点且v是u的一个邻接点.我们用N（v）表示点v的邻接点集

合.我们知道v的邻接点数目也叫作这个点的度，用deg v表示.

我们说图G是奇怪的如果它是连通的且对于它的每一个点满足如下条件：

1. 点v的度deg v>=2（表明v的邻接点至少有两个）

2. 如果点v的度deg v=2，那么它的两个邻接点之间没有边相连

3. 如果点v的度deg v>2，那么在它的邻接点集合N（v）中存在点u满足：

（a）点u的度deg u=2

（b）集合N（v）中除顶点u外任意两个不同的点是相邻的，即（w1，w2）这条边存在于边集E中.

现在给你某个这样的图，在里面找出一条哈密尔顿回路，一条哈密尔顿回路就是一条回路，这条回路经过图G中的每一点，且只经过一次.

输入

       输入文件的第一行包含两个整数N和M——N为图G中定点的数目，M为图G中边的数目

（3<=N<=10000，M<=100000）.接下来为2M个整数（每相邻两个点为一对）——每对数代表一条边的两个顶点（顶点被编号为1-N）.输入数据保证每条边仅出现一次，且没有这样的环（边的两端点相同）.

输出

       如果在图G中没有哈密尔顿回路，则在输出文件的第一行输出-1.如果存在,则输出N个数——即在图G中找到的哈密尔顿回路的顶点序列（注意：最后一个点必须与第一个点相连）.

如果有多种解，则输出任意一种即可.

Sample input #1

4 4

1 2 2 3 3 4 4 1

Sample input #2

9 12

1 2 2 3 3 1 1 4 2 5 3 6

4 7 5 8 6 9 7 8 8 9 9 7

Sample output #1

1 2 3 4

Sample output #2

-1

 

 

 

---

 

分析：

      给出一个联通的图，保证每个点的度至少为2.

      并且对于度大于2的点，相连的有一个度为2的点，其它相连的点之间都有边。

      对于这个图求它的哈密顿回路。

      先来分析这个奇怪的图，从样例2也可以看出对于这样的图是无法保证有解的。

      从这里似乎需要判断哈密顿回路的存在与否，但是判断哈密顿回路的存在问题是NP的。

      这就使得我们转换思路。

      回忆起SGU的SGU 101.Domino（多米诺骨牌），在这一题，我们放弃寻找一个哈密顿路，重新建图变成了一个求欧拉路的问题。

      这里是不是也可以呢？

      考虑一个点u，假设它与a，b，v相连，

      v是一个度为2的点，那么a，b之间一定有边，并且它们还有一条边连向一个度为2的节点

      

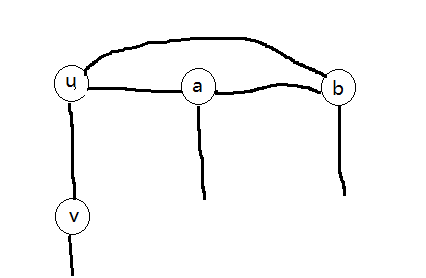
      显然边G（u,a,b）是一个完全图，而且能够以任意方式互相遍历

  　 这时我们可以将V(u,a,b)看成一个点。

      接下来的问题就是求新得到的图的欧拉回路了。

　   每次进入完全子图时，走不同的边。

      时间复杂度O（n+m）；

     

code（46ms    AC）

/*

       前向星存边，对于一个完全子图用并查集进行合并,存入f[].

       寻找欧拉路时每次只在一个完全子图中用一条边,并标记走过的点,直接输出答案.

*/

#include <iostream>

#include <cstdio>

#include <cstring>

using namespace std;

const int INF = int (1e4 + 9);

//前向星存边

struct Edge {

	int u, v, ne;

} edge[INF * 20];

int head[INF], deg[INF], vise[INF * 20], vis[INF], f[INF], cnt = 1;

int n, m, x, y;



void addedge (int u, int v) {

	edge[++cnt].u = u, edge[cnt].v = v;

	edge[cnt].ne = head[u], head[u] = cnt;

}

//合并完全子图

void change() {

	for (int i = 1; i <= n; i++)

		if (deg[i] > 2 && !vis[i]) {

			for (int j = head[i]; j != 0; j = edge[j].ne) {

				int v = edge[j].v;

				if (deg[v] > 2)

					f[v] = i, vis[v] = 1;

			}

		}

}

void EulerianPath (int x, int p) {

	vis[x] = 1;

	for (int i = head[x]; i != 0; i = edge[i].ne) {

		if (vise[i] || vis[edge[i].v]) continue;

		int u = edge[i].u, v = edge[i].v;

		if (p && f[u] == f[v]) {

			vise[i] = vise[i ^ 1] = 1;

			//由内传来

			EulerianPath (v, 0);

		}

		if (deg[x] == 2 || (!p && f[u] != f[v]) ) {

			vise[i] = vise[i ^ 1] = 1;

			//由外传来

			EulerianPath (v, 1);

		}

	}

	printf ("%d ", x);

}

//判断并寻找欧拉回路

void Eulerian() {

	int t = 0;

	for (int i = 1; i <= n; i++) {

		if (!f[i] && deg[i] & 1) {

			t++; break;

		}

		if (!f[i]) f[i] = i;

	}

	if (t != 0) {

		puts ("-1"); return;

	}

	memset (vis, 0, sizeof vis);

	EulerianPath (1, 0);//如果存在哈密顿回路以任意起点出发均可

}

int main() {

	scanf ("%d %d", &n, &m);

	for (int i = 1; i <= m; i++) {

		scanf ("%d %d", &x, &y);

		addedge (x, y), addedge (y, x);

		deg[x]++, deg[y]++;

	}

	change();

	Eulerian();

	return 0;

}