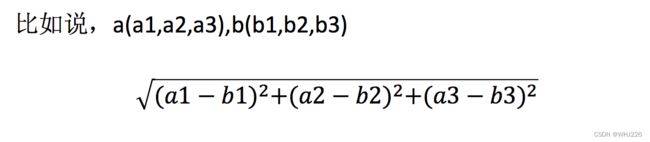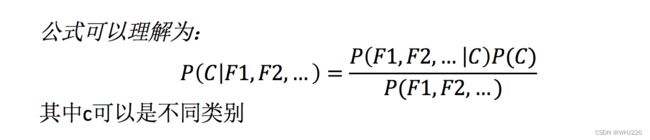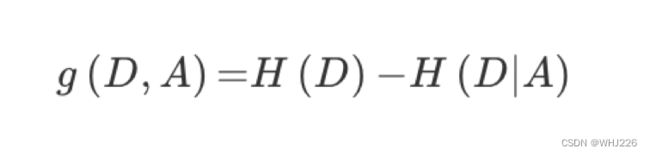机器学习（18）——分类算法（补充）

目录

1 sklearn转换器和估计器

1.1 转换器

1.2 估计器

2 K-近邻算法(KNN)

2.1 案例1——鸢尾花种类预测

3 模型选择与调优

3.1 什么是交叉验证(cross validation)

3.2 超参数搜索-网格搜索(Grid Search)

3.2.1 模型选择与调优

3.3 案例2——预测facebook签到位置

4 朴素贝叶斯算法

4.1 拉普拉斯平滑系数

5 决策树

5.1 信息熵、信息增益

5.2 案例3——用决策树对鸢尾花进行分类

5.3 案例4——泰坦尼克号乘客生存预测 

6 随机森林

---

本篇博文将对sklearn的转换器和估计器流程、sklearn的分类、回归数据集、K-近邻算法的距离公式、K-近邻算法的超参数K值以及取值问题、K-近邻算法的优缺点、应用KNeighborsClassifier实现分类、了解分类算法的评估标准准确率、说明朴素贝叶斯算法的原理、说明朴素贝叶斯算法的优缺点、应用MultinomialNB实现文本分类、应用模型选择与调优、说明决策树算法的原理、说明决策树算法的优缺点、应用DecisionTreeClassifier实现分类、说明随机森林算法的原理、说明随机森林算法的优缺点以及应用RandomForestClassifier实现分类 。

1 sklearn转换器和估计器

1.1 转换器

特征工程步骤如下：

• 1、实例化 (实例化的是一个转换器类(Transformer))
• 2、调用fit_transform(对于文档建立分类词频矩阵，不能同时调用)

我们把特征工程的接口称之为转换器，其中转换器调用有这么几种形式：

• fit--->计算
• transform--->转换
• fit_transform--->计算+转换

我们用代码演示一下这几种形式的区别：

from sklearn.preprocessing import StandardScaler

a = [[7,8,9], [10, 11, 12]]
std1 = StandardScaler()
print("fit:\n",std1.fit(a))
print("transform:\n",std1.transform(a))
print("fit_transform:\n",std1.fit_transform(a))

运行结果如下：

fit:
 StandardScaler()
transform:
 [[-1. -1. -1.]
 [ 1.  1.  1.]]
fit_transform:
 [[-1. -1. -1.]
 [ 1.  1.  1.]]

从中可以看出，fit_transform的作用相当于transform加上fit。

1.2 估计器

在sklearn中，估计器(estimator)是一个重要的角色，是一类实现了算法的API：

• 1、用于分类的估计器：
  • sklearn.neighbors k-近邻算法
  • sklearn.naive_bayes 贝叶斯
  • sklearn.linear_model.LogisticRegression 逻辑回归
  • sklearn.tree 决策树与随机森林
• 2、用于回归的估计器：
  • sklearn.linear_model.LinearRegression 线性回归
  • sklearn.linear_model.Ridge 岭回归
• 3、用于无监督学习的估计器
  • sklearn.cluster.KMeans 聚类

工作流程：

估计器：

1 实例化一个estimator

2 estimator.fit(x_train,y_train)计算--->调用完毕，模型生成

3 模型评估：

1）直接比对真实值和预测值

y_predict = estimator.predict(x_test)

y_test == y_predict

2)计算准确率

accuracy = estimator.score(x_test,y_test) 

2 K-近邻算法(KNN)

定义：

如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。

那么如何确定谁是邻居呢？

距离公式：

欧式距离、曼哈顿距离、明科夫斯基距离等。欧式距离计算公式如下：

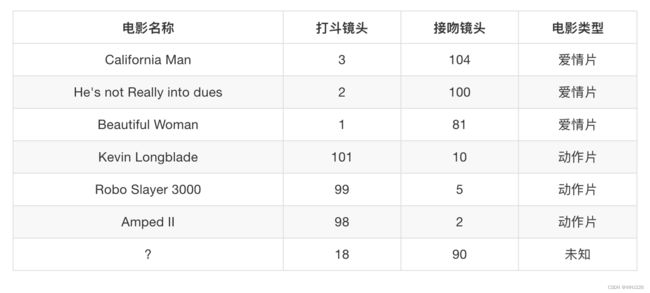
假设我们有现在几部电影：

其中？号电影不知道类别，如何去预测？我们可以利用K近邻算法的思想。

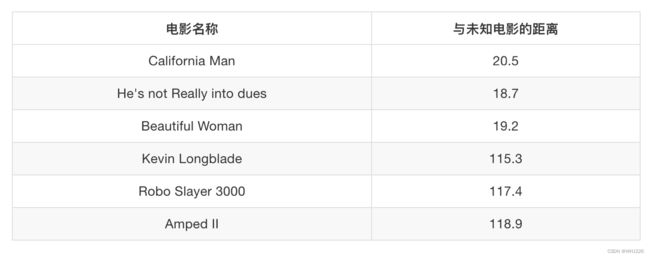
如果取的最近的电影数量不一样？会是什么结果？

k=1 爱情片（取距离最近的1个样本，该样本为爱情片，所以为爱情片）。

k=2 爱情片（取距离最近的2个样本，该样本为爱情片，所以为爱情片）。

...

k=6 无法确定（取距离最近的6个样本，该样本中3个爱情片，3个动作片，最终无法确定）。

k=1 容易受到异常点的影响。

k取值过大，受到样本不均衡的影响。

K-近邻算法API：

sklearn.neighbors.KNeighborsClassifier(n_neighbors=5,algorithm='auto')

• n_neighbors：int,可选（默认= 5），k_neighbors查询默认使用的邻居数
• algorithm：{‘auto’，‘ball_tree’，‘kd_tree’，‘brute’}，可选用于计算最近邻居的算法：‘ball_tree’将会使用 BallTree，‘kd_tree’将使用 KDTree，‘auto’将尝试根据传递给fit方法的值来决定最合适的算法。 (不同实现方式影响效率)

2.1 案例1——鸢尾花种类预测

用knn算法对鸢尾花进行分类：

1、获取数据

2、数据集划分

3、特征工程：标准化

4、KNN算法预估器

5、模型评估：

     1）直接比对真实值和预测值

     2）计算准确率

代码如下：

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
def knn_iris():
    """
    用knn算法对鸢尾花进行分类
    :return:
    """
    # 1、获取数据
    iris = load_iris()
    # 2、数据集划分
    x_train, x_test, y_train, y_test = train_test_split(iris.data,iris.target,random_state=6)
    # 3、特征工程：标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test) #训练集fit，测试集不fit，因为实际我们不知道要分类的未知数据，所以标准化的平均值和标准差只能用测试集的
    # 4、KNN算法预估器
    estimator = KNeighborsClassifier(n_neighbors=3)
    estimator.fit(x_train,y_train)
    # 5、模型评估
    # 1）直接比对真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:\n",y_predict)
    print("直接比对真实值和预测值:\n", y_test == y_predict)
    # 2)计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率:\n",score)
    return None


if __name__ == "__main__":
    #代码：用knn算法对鸢尾花进行分类
    knn_iris()

运行结果如下：

y_predict:
 [0 2 0 0 2 1 1 0 2 1 2 1 2 2 1 1 2 1 1 0 0 2 0 0 1 1 1 2 0 1 0 1 0 0 1 2 1
 2]
直接比对真实值和预测值:
 [ True  True  True  True  True  True False  True  True  True  True  True
  True  True  True False  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True False  True
  True  True]
准确率:
 0.9210526315789473

总结：

• 1、k值取多大？有什么影响？

k值取很小：容易受到异常点的影响

k值取很大：受到样本均衡的问题

• 2、性能问题？

距离计算上面，时间复杂度高

• 优点：
  • 简单，易于理解，易于实现，无需训练
• 缺点：
  • 懒惰算法，对测试样本分类时的计算量大，内存开销大
  • 必须指定K值，K值选择不当则分类精度不能保证
• 使用场景：小数据场景，几千～几万样本，具体场景具体业务去测试

3 模型选择与调优

3.1 什么是交叉验证(cross validation)

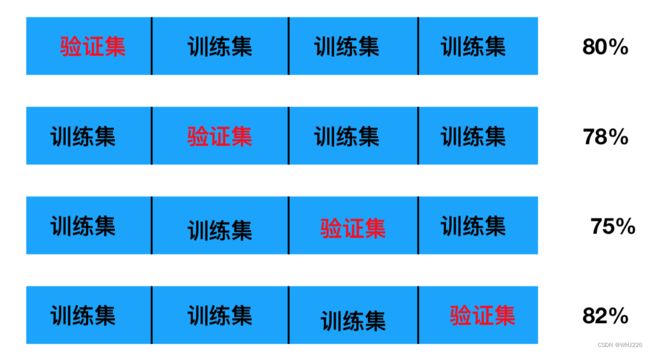
交叉验证：将拿到的训练数据，分为训练和验证集。以下图为例：将数据分成5份，其中一份作为验证集。然后经过5次(组)的测试，每次都更换不同的验证集。即得到5组模型的结果，取平均值作为最终结果。又称5折交叉验证。

为什么需要交叉验证？--->为了让被评估的模型更加准确可信。

那么这个只是对于参数得出更好的结果，那么怎么选择或者调优参数呢？

3.2 超参数搜索-网格搜索(Grid Search)

通常情况下，有很多参数是需要手动指定的（如k-近邻算法中的K值），这种叫超参数。但是手动过程繁杂，所以需要对模型预设几种超参数组合。每组超参数都采用交叉验证来进行评估。最后选出最优参数组合建立模型。

3.2.1 模型选择与调优

sklearn.model_selection.GridSearchCV(estimator, param_grid=None,cv=None)

• 对估计器的指定参数值进行详尽搜索
• estimator：估计器对象
• param_grid：估计器参数(dict){“n_neighbors”:[1,3,5]}（字典类型）
• cv：指定几折交叉验证
• fit：输入训练数据
• score：准确率
• 结果分析：
• 最佳参数：best_params_
• 最佳结果：best_score_
• 最佳预估器：best_estimator_
• 交叉验证结果：cv_results_

下面，我们用knn算法对鸢尾花进行分类，并添加网格搜索和交叉验证。

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import GridSearchCV
def knn_iris_gscv():
    """
    用knn算法对鸢尾花进行分类，添加网格搜索和交叉验证
    :return:
    """
    # 1、获取数据
    iris = load_iris()
    # 2、数据集划分
    x_train, x_test, y_train, y_test = train_test_split(iris.data,iris.target,random_state=6)
    # 3、特征工程：标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test) #训练集fit，测试集不fit，因为实际我们不知道要分类的未知数据，所以标准化的平均值和标准差只能用测试集的
    # 4、KNN算法预估器
    estimator = KNeighborsClassifier()
    #加入网格搜索与交叉验证
    #参数准备
    param_dict = {"n_neighbors":[1,3,5,7,9,11]}
    estimator = GridSearchCV(estimator,param_grid=param_dict,cv=10)
    estimator.fit(x_train,y_train)
    # 5、模型评估
    # 1）直接比对真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:\n",y_predict)
    print("直接比对真实值和预测值:\n", y_test == y_predict)
    # 2)计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率:\n",score)
    # 最佳参数：best_params_
    print("最佳参数:\n", estimator.best_params_)
    # 最佳结果：best_score_
    print("最佳结果:\n", estimator.best_score_)
    # 最佳预估器：best_estimator_
    print("最佳预估器:\n", estimator.best_estimator_)
    # 交叉验证结果：cv_results_
    print("交叉验证结果:\n", estimator.cv_results_)
    return None


if __name__ == "__main__":
    #代码：用knn算法对鸢尾花进行分类，添加网格搜索和交叉验证
    knn_iris_gscv()

 运行结果如下：

y_predict:
 [0 2 0 0 2 1 2 0 2 1 2 1 2 2 1 1 2 1 1 0 0 2 0 0 1 1 1 2 0 1 0 1 0 0 1 2 1
 2]
直接比对真实值和预测值:
 [ True  True  True  True  True  True  True  True  True  True  True  True
  True  True  True False  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True False  True
  True  True]
准确率:
 0.9473684210526315
最佳参数:
 {'n_neighbors': 11}
最佳结果:
 0.9734848484848484
最佳预估器:
 KNeighborsClassifier(n_neighbors=11)
交叉验证结果:
 {'mean_fit_time': array([0.00086534, 0.00059962, 0.00075936, 0.00080037, 0.00040061,
       0.00049934]), 'std_fit_time': array([0.00133643, 0.00048959, 0.00050251, 0.00040019, 0.00049067,
       0.00049935]), 'mean_score_time': array([0.00142319, 0.00120194, 0.0012007 , 0.0014998 , 0.0012012 ,
       0.00159819]), 'std_score_time': array([0.00062137, 0.00039834, 0.00039953, 0.00050006, 0.00039969,
       0.00066429]), 'param_n_neighbors': masked_array(data=[1, 3, 5, 7, 9, 11],
             mask=[False, False, False, False, False, False],
       fill_value='?',
            dtype=object), 'params': [{'n_neighbors': 1}, {'n_neighbors': 3}, {'n_neighbors': 5}, {'n_neighbors': 7}, {'n_neighbors': 9}, {'n_neighbors': 11}], 'split0_test_score': array([1., 1., 1., 1., 1., 1.]), 'split1_test_score': array([0.91666667, 0.91666667, 1.        , 0.91666667, 0.91666667,
       0.91666667]), 'split2_test_score': array([1., 1., 1., 1., 1., 1.]), 'split3_test_score': array([1.        , 1.        , 1.        , 1.        , 0.90909091,
       1.        ]), 'split4_test_score': array([1., 1., 1., 1., 1., 1.]), 'split5_test_score': array([0.90909091, 0.90909091, 1.        , 1.        , 1.        ,
       1.        ]), 'split6_test_score': array([1., 1., 1., 1., 1., 1.]), 'split7_test_score': array([0.90909091, 0.90909091, 0.90909091, 0.90909091, 1.        ,
       1.        ]), 'split8_test_score': array([1., 1., 1., 1., 1., 1.]), 'split9_test_score': array([0.90909091, 0.81818182, 0.81818182, 0.81818182, 0.81818182,
       0.81818182]), 'mean_test_score': array([0.96439394, 0.95530303, 0.97272727, 0.96439394, 0.96439394,
       0.97348485]), 'std_test_score': array([0.04365767, 0.0604591 , 0.05821022, 0.05965639, 0.05965639,
       0.05742104]), 'rank_test_score': array([5, 6, 2, 3, 3, 1])}

3.3 案例2——预测facebook签到位置

数据介绍：将根据用户的位置，准确性和时间戳预测用户正在查看的业务。

train.csv，test.csv 
row_id：登记事件的ID
xy：坐标
准确性：定位准确性 
时间：时间戳
place_id：业务的ID，这是您预测的目标

数据来源：官网：grid_knn | Kaggle 

分析：

• 对于数据做一些基本处理（这里所做的一些处理不一定达到很好的效果，我们只是简单尝试，有些特征我们可以根据一些特征选择的方式去做处理）

  • 1、缩小数据集范围 DataFrame.query()

  • 4、删除没用的日期数据 DataFrame.drop（可以选择保留）

  • 5、将签到位置少于n个用户的删除

    place_count = data.groupby('place_id').count()

    tf = place_count[place_count.row_id > 3].reset_index()

    data = data[data['place_id'].isin(tf.place_id)]

• 分割数据集

• 标准化处理

• k-近邻预测

首先，用knn算法：

df.query():

pandas41 query-字符串表达式查询：大数据函数( tcy）_tcy23456的博客-CSDN博客_pandas query 字符串

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier

def knncls():
    """
    K近邻算法预测入住位置类别
    :return:
    """
    # 一、处理数据以及特征工程
    # 1、读取收，缩小数据的范围
    data = pd.read_csv("F:/BaiduNetdiskDownload/mechine learning/Machine_Learning/resources/FBlocation/train.csv")

    # 数据逻辑筛选操作 df.query()
    data = data.query("x > 1.0 & x < 1.25 & y > 2.5 & y < 2.75")

    # 删除time这一列特征
    data = data.drop(['time'], axis=1)

    print(data)

    # 删除入住次数少于三次位置
    place_count = data.groupby('place_id').count()

    tf = place_count[place_count.row_id > 3].reset_index()

    data = data[data['place_id'].isin(tf.place_id)]

    # 3、取出特征值和目标值
    y = data['place_id']
    x = data.drop(['place_id', 'row_id'], axis=1)

    # 4、数据分割与特征工程?

    # （1）、数据分割
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3)

    # (2)、标准化
    std = StandardScaler()

    # 队训练集进行标准化操作
    x_train = std.fit_transform(x_train)
    print(x_train)

    # 进行测试集的标准化操作
    x_test = std.fit_transform(x_test)

    # 二、算法的输入训练预测
    # K值：算法传入参数不定的值    理论上：k = 根号(样本数)
    # K值：后面会使用参数调优方法，去轮流试出最好的参数[1,3,5,10,20,100,200]
    knn = KNeighborsClassifier(n_neighbors=1)

    # 调用fit()
    knn.fit(x_train, y_train)

    # 预测测试数据集，得出准确率
    y_predict = knn.predict(x_test)

    print("预测测试集类别：", y_predict)

    print("准确率为：", knn.score(x_test, y_test))

    return None

if __name__ == "__main__":
    #代码：用knn算法对鸢尾花进行分类，添加网格搜索和交叉验证
    knncls()

运行结果如下： 

            row_id       x       y  accuracy    place_id
600            600  1.2214  2.7023        17  6683426742
957            957  1.1832  2.6891        58  6683426742
4345          4345  1.1935  2.6550        11  6889790653
4735          4735  1.1452  2.6074        49  6822359752
5580          5580  1.0089  2.7287        19  1527921905
...            ...     ...     ...       ...         ...
29100203  29100203  1.0129  2.6775        12  3312463746
29108443  29108443  1.1474  2.6840        36  3533177779
29109993  29109993  1.0240  2.7238        62  6424972551
29111539  29111539  1.2032  2.6796        87  3533177779
29112154  29112154  1.1070  2.5419       178  4932578245

[17710 rows x 5 columns]
[[ 0.83245563 -1.74343908  0.05714877]
 [ 0.52915898  0.49524962 -0.13620476]
 [-0.85122962  0.69993791 -0.15461938]
 ...
 [ 0.09495224 -1.37557271 -0.14541207]
 [ 0.46175972  0.93897948 -0.56894839]
 [ 0.52397442 -0.82448886  2.92062257]]
预测测试集类别： [5161681408 1097200869 3533177779 ... 2584530303 6237569496 6683426742]
准确率为： 0.40070921985815605

其次，预测K值调优，我们将会在jupyter中进行运算：

• 使用网格搜索估计器
• 流程分析：
• 1、获取数据
• 2、数据处理 目的： 特征值 x 目标值 y
• a.缩小数据范围 2
• b.time->年月日时分秒
• 3、特征工程：标准化
• 4、KNN算法预估流程
• 5、模型选择与调优
• 6、模型评估

pd.to_datetime:

 python的时间转换datetime和pd.to_datetime_-永不妥协-的博客-CSDN博客_python to_datetime

pd.to_datetime()_Kwoky的博客-CSDN博客_pd.to_datetime用法

import pandas as pd
#1、获取数据
data = pd.read_csv("F:/BaiduNetdiskDownload/mechine learning/Machine_Learning/resources/FBlocation/train.csv")

#2、基本数据处理
#1）缩小数据范围
data = data.query("x < 2.5 & x >2 & y< 1.5 & y > 1.0") # 数据逻辑筛选操作 df.query()
#2)处理时间特征
time_value = pd.to_datetime(data["time"],unit="s")
date = pd.DatetimeIndex(time_value)
data["day"] = date.day
data["weekday"] = date.weekday
data["hour"] = date.hour
#3)过滤签到次数少的地点
place_count = data.groupby("place_id").count()["row_id"]
#data.groupby("place_id").count() #统计数量
#place_count[place_count > 3].head()
data_final = data[data["place_id"].isin(place_count[place_count > 3].index.values)]
#筛选目标值和特征值
x = data_final[["x","y","accuracy","day","weekday","hour"]]
y = data_final["place_id"]
#数据集划分
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x,y)

from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import GridSearchCV

# 3、特征工程：标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test) #训练集fit，测试集不fit，因为实际我们不知道要分类的未知数据，所以标准化的平均值和标准差只能用测试集的
# 4、KNN算法预估器
estimator = KNeighborsClassifier()
#加入网格搜索与交叉验证
#参数准备
param_dict = {"n_neighbors":[3,5,7,9]}
estimator = GridSearchCV(estimator,param_grid=param_dict,cv=3)
estimator.fit(x_train,y_train)
# 5、模型评估
# 1）直接比对真实值和预测值
y_predict = estimator.predict(x_test)
print("y_predict:\n",y_predict)
print("直接比对真实值和预测值:\n", y_test == y_predict)
# 2)计算准确率
score = estimator.score(x_test, y_test)
print("准确率:\n",score)
# 最佳参数：best_params_
print("最佳参数:\n", estimator.best_params_)
# 最佳结果：best_score_
print("最佳结果:\n", estimator.best_score_)
# 最佳预估器：best_estimator_
print("最佳预估器:\n", estimator.best_estimator_)
# 交叉验证结果：cv_results_
print("交叉验证结果:\n", estimator.cv_results_)

运行结果如下： 

y_predict:
 [1540382716 3229876087 2852927300 ... 6706708436 1327075245 5632997879]
直接比对真实值和预测值:
 14668111    False
27343822     True
15103904    False
1073508     False
22672114    False
            ...  
25579756    False
14532786     True
20000562     True
8492671     False
819453       True
Name: place_id, Length: 20228, dtype: bool
准确率:
 0.36607672533122404
最佳参数:
 {'n_neighbors': 7}
最佳结果:
 0.33528883188596975
最佳预估器:
 KNeighborsClassifier(n_neighbors=7)
交叉验证结果:
 {'mean_fit_time': array([0.10567093, 0.08900865, 0.08966986, 0.09933988]), 'std_fit_time': array([0.01061762, 0.00245127, 0.00589601, 0.00680692]), 'mean_score_time': array([1.00040642, 0.98540219, 1.09007986, 1.15351415]), 'std_score_time': array([0.04896799, 0.01601261, 0.03288546, 0.08910883]), 'param_n_neighbors': masked_array(data=[3, 5, 7, 9],
             mask=[False, False, False, False],
       fill_value='?',
            dtype=object), 'params': [{'n_neighbors': 3}, {'n_neighbors': 5}, {'n_neighbors': 7}, {'n_neighbors': 9}], 'split0_test_score': array([0.3230176 , 0.33789796, 0.33839233, 0.3321139 ]), 'split1_test_score': array([0.32367627, 0.33395956, 0.33252583, 0.3277797 ]), 'split2_test_score': array([0.32347852, 0.33351461, 0.33494834, 0.3322292 ]), 'mean_test_score': array([0.3233908 , 0.33512404, 0.33528883, 0.3307076 ]), 'std_test_score': array([0.00027596, 0.00196985, 0.00240706, 0.00207087]), 'rank_test_score': array([4, 2, 1, 3])}

4 朴素贝叶斯算法

条件概率与联合概率：

• 联合概率：包含多个条件，且所有条件同时成立的概率
  • 记作：P(A,B)
  • 特性：P(A, B) = P(A)P(B)
• 条件概率：就是事件A在另外一个事件B已经发生条件下的发生概率
  • 记作：P(A|B)
  • 特性：P(A1,A2|B) = P(A1|B)P(A2|B) 注意：此条件概率的成立，是由于A1,A2相互独立的结果

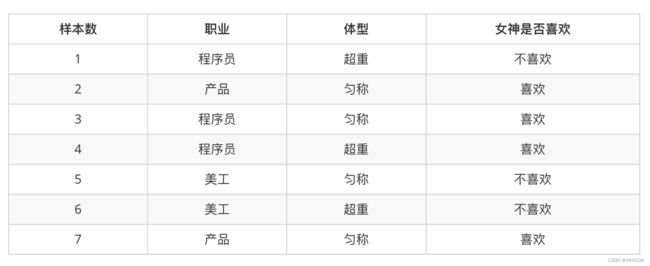
我们通过一个例子，来计算一些结果：

这样我们计算结果为：

p(程序员, 匀称) =  P(程序员)P(匀称) =3/7*(4/7) = 12/49 
P(产品, 超重|喜欢) = P(产品|喜欢)P(超重|喜欢)=1/2 *  1/4 = 1/8

朴素贝叶斯如何分类，这个算法经常会用在文本分类，那就来看文章分类是一个什么样的问题？

这个了类似一个条件概率，那么仔细一想，给定文章其实相当于给定什么？结合前面我们将文本特征抽取的时候讲的？所以我们可以理解为

 但是这个公式怎么求？前面并没有参考例子，其实是相似的，我们可以使用贝叶斯公式去计算 。

贝叶斯公式：

 那么这个公式如果应用在文章分类的场景当中，我们可以这样看：

公式分为三个部分：

• P(C)：每个文档类别的概率(某文档类别数／总文档数量)
• P(W│C)：给定类别下特征（被预测文档中出现的词）的概率
  • 计算方法：P(F1│C)=Ni/N （训练文档中去计算）
    • Ni为该F1词在C类别所有文档中出现的次数
    • N为所属类别C下的文档所有词出现的次数和
• P(F1,F2,…) 预测文档中每个词的概率

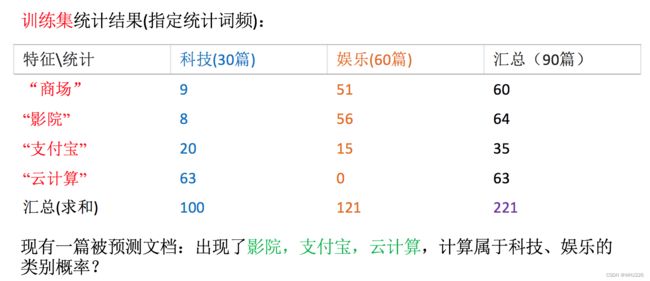
• 假设我们从训练数据集得到如下信息

• 计算结果

科技：P(科技|影院,支付宝,云计算) = (影院,支付宝,云计算|科技)∗P(科技)=(8/100)∗(20/100)∗(63/100)∗(30/90) = 0.00456109

娱乐：P(娱乐|影院,支付宝,云计算) = (影院,支付宝,云计算|娱乐)∗P(娱乐)=(56/121)∗(15/121)∗(0/121)∗(60/90) = 0

我们计算出来某个概率为0，合适吗？

4.1 拉普拉斯平滑系数

目的：防止计算出的分类概率为0。

P(娱乐|影院,支付宝,云计算) =P(影院,支付宝,云计算|娱乐)P(娱乐) =P(影院|娱乐)*P(支付宝|娱乐)*P(云计算|娱乐)P(娱乐)=(56+1/121+4)(15+1/121+4)(0+1/121+1*4)(60/90) = 0.00002

sklearn.naive_bayes.MultinomialNB(alpha = 1.0)

• 朴素贝叶斯分类
• alpha：拉普拉斯平滑系数

案例：20类新闻分类

 1）获取数据

2）划分数据集

3）特征工程 文本特征抽取

4）朴素贝叶斯预估器流程

5）模型评估

代码如下：

def nbcls():
    """
    朴素贝叶斯对新闻数据集进行预测
    :return:
    """
    # 获取新闻的数据，20个类别
    news = fetch_20newsgroups(subset='all')

    # 进行数据集分割
    x_train, x_test, y_train, y_test = train_test_split(news.data, news.target, test_size=0.3)

    # 对于文本数据，进行特征抽取
    tf = TfidfVectorizer()

    x_train = tf.fit_transform(x_train)
    # 这里打印出来的列表是：训练集当中的所有不同词的组成的一个列表
    print(tf.get_feature_names())
    # print(x_train.toarray())

    # 不能调用fit_transform
    x_test = tf.transform(x_test)

    # estimator估计器流程
    mlb = MultinomialNB(alpha=1.0)

    mlb.fit(x_train, y_train)

    # 进行预测
    y_predict = mlb.predict(x_test)

    print("预测每篇文章的类别：", y_predict[:100])
    print("真实类别为：", y_test[:100])

    print("预测准确率为：", mlb.score(x_test, y_test))

    return None

在学习中未找到20newsgroups数据，所以在此将代码附上。

总结：

• 优点：
  • 朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。
  • 对缺失数据不太敏感，算法也比较简单，常用于文本分类。
  • 分类准确度高，速度快
• 缺点：
  • 由于使用了样本属性独立性的假设，所以如果特征属性有关联时其效果不好

5 决策树

决策树思想的来源非常朴素，程序设计中的条件分支结构就是if-then结构，最早的决策树就是利用这类结构分割数据的一种分类学习方法

怎么理解这句话？通过一个对话例子。

我们要理解为什么我们会把年龄放在第一位？可以利用当得知某个特征（比如年龄）之后，我们能够减少的不确定性大小。越大我们可以认为这个特征很重要。那怎么去衡量减少的不确定性大小呢？

5.1 信息熵、信息增益

• H的专业术语称之为信息熵，单位为比特。

 决策树的划分依据之一------信息增益

定义与公式：

特征A对训练数据集D的信息增益g(D,A),定义为集合D的信息熵H(D)与特征A给定条件下D的信息条件熵H(D|A)之差，即公式为：

公式的详细解释：

注：信息增益表示得知特征X的信息而息的不确定性减少的程度使得类Y的信息熵减少的程度。

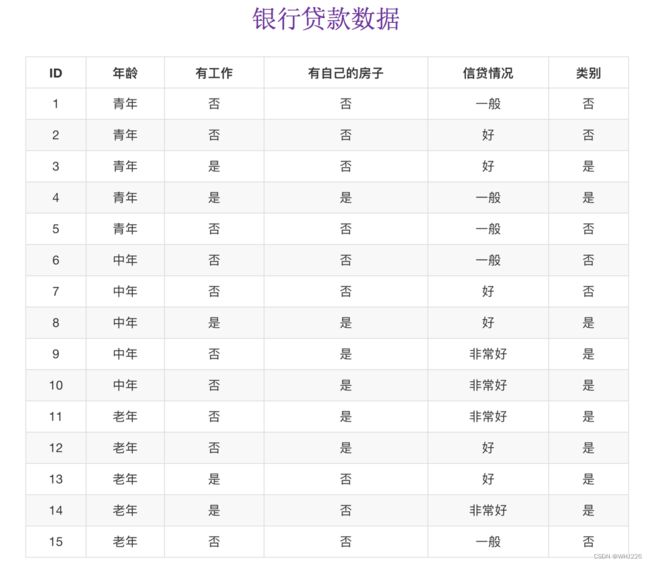
• 我们以年龄特征来计算：

1、g(D, 年龄) = H(D) -H(D|年龄) = 0.971-[5/15H(青年)+5/15H(中年)+5/15H(老年]

2、H(D) = -(6/15log(6/15)+9/15log(9/15))=0.971

3、H(青年) = -(3/5log(3/5) +2/5log(2/5))
H(中年)=-(3/5log(3/5) +2/5log(2/5))
H(老年)=-(4/5og(4/5)+1/5log(1/5))

 我们以A1、A2、A3、A4代表年龄、有工作、有自己的房子和贷款情况。最终计算的结果g(D, A1) = 0.313, g(D, A2) = 0.324, g(D, A3) = 0.420,g(D, A4) = 0.363。所以我们选择A3 作为划分的第一个特征。

决策树API：

• class sklearn.tree.DecisionTreeClassifier(criterion=’gini’, max_depth=None,random_state=None)
  • 决策树分类器
  • criterion:默认是’gini’系数，也可以选择信息增益的熵’entropy’
  • max_depth:树的深度大小
  • random_state:随机数种子
• 其中会有些超参数：max_depth:树的深度大小
  • 其它超参数我们会结合随机森林讲解

5.2 案例3——用决策树对鸢尾花进行分类

代码如下：

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier,export_graphviz
def decision_iris():
    """
    用决策树对鸢尾花进行分类
    :return:
    """
    # 1）获取数据集
    iris = load_iris()
    # 2）划分数据集
    x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=6)
    # 3）决策树预估器
    estimator = DecisionTreeClassifier(criterion="entropy")
    estimator.fit(x_train, y_train)
    # 4）模型评估
    # 5、模型评估
    # 1）直接比对真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:\n", y_predict)
    print("直接比对真实值和预测值:\n", y_test == y_predict)
    # 2)计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率:\n", score)
    #可视化决策树
    #网站显示结构：http://webgraphviz.com/
    #http://dreampuf.github.io/GraphvizOnline/将dot文件内容复制该网站即可，等待一会出图
    export_graphviz(estimator,out_file="iris_tree.dot")

    return None

if __name__ == "__main__":
    #用决策树对鸢尾花进行分类
    decision_iris()

运行结果如下：

            row_id       x       y  accuracy    place_id
600            600  1.2214  2.7023        17  6683426742
957            957  1.1832  2.6891        58  6683426742
4345          4345  1.1935  2.6550        11  6889790653
4735          4735  1.1452  2.6074        49  6822359752
5580          5580  1.0089  2.7287        19  1527921905
...            ...     ...     ...       ...         ...
29100203  29100203  1.0129  2.6775        12  3312463746
29108443  29108443  1.1474  2.6840        36  3533177779
29109993  29109993  1.0240  2.7238        62  6424972551
29111539  29111539  1.2032  2.6796        87  3533177779
29112154  29112154  1.1070  2.5419       178  4932578245

[17710 rows x 5 columns]
[[ 1.50934208  1.58599493 -0.18615452]
 [-1.02465789 -1.31117571 -0.1497283 ]
 [-0.27183094 -0.82998474 -0.14062175]
 ...
 [-0.20715509  0.15531106 -0.24079384]
 [-1.38684267 -0.71541546 -0.10419553]
 [ 0.63621805 -1.4715727  -0.13151519]]
预测测试集类别： [5009192468 5261906348 8048985799 ... 6683426742 3202755803 6399991653]
准确率为： 0.40622537431048067
y_predict:
 [0 2 0 0 2 1 1 0 2 1 2 1 2 2 1 1 2 1 1 0 0 2 0 0 1 1 1 2 0 1 0 1 0 0 1 2 1
 2]
直接比对真实值和预测值:
 [ True  True  True  True  True  True False  True  True  True  True  True
  True  True  True False  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True False  True
  True  True]
准确率:
 0.9210526315789473

保存树的结构到dot文件:

• 1、sklearn.tree.export_graphviz() 该函数能够导出DOT格式
  • tree.export_graphviz(estimator,out_file='tree.dot’,feature_names=[‘’,’’])
• 2、工具:(能够将dot文件转换为pdf、png)
  • 安装graphviz
  • ubuntu:sudo apt-get install graphviz Mac:brew install graphviz
• 3、运行命令
  • 然后我们运行这个命令
  • dot -Tpng tree.dot -o tree.png

export_graphviz(dc, out_file="./tree.dot", feature_names=['age', 'pclass=1st', 'pclass=2nd', 'pclass=3rd', '女性', '男性'])

可视化决策树：

我们可以通过http://dreampuf.github.io/GraphvizOnline/将dot文件内容复制该网站即可，等待一会出图。

5.3 案例4——泰坦尼克号乘客生存预测 

在泰坦尼克号和titanic2数据帧描述泰坦尼克号上的个别乘客的生存状态。这里使用的数据集是由各种研究人员开始的。其中包括许多研究人员创建的旅客名单，由Michael A. Findlay编辑。我们提取的数据集中的特征是票的类别，存活，乘坐班，年龄，登陆，home.dest，房间，票，船和性别。

1、乘坐班是指乘客班（1，2，3），是社会经济阶层的代表。

2、其中age数据存在缺失。

数据：http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt

分析：

• 选择我们认为重要的几个特征 ['pclass', 'age', 'sex']
• 填充缺失值
• 特征中出现类别符号，需要进行one-hot编码处理(DictVectorizer)
  • x.to_dict(orient="records") 需要将数组特征转换成字典数据
• 数据集划分
• 决策树分类预测

流程分析：

特征值 目标值

1）获取数据

2）数据处理 缺失值处理 特征值->字典类型

3）准备好特征值，目标值

4）划分数据集

5）特征工程：字典特征抽取

6）决策树预估器流程

7）模型评估

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction import DictVectorizer
from sklearn.tree import DecisionTreeClassifier,export_graphviz
#1）获取数据
titanic = pd.read_csv("titanic.csv")
# print(titanic)
#筛选特征值和目标值
x = titanic[["pclass","age","sex"]]
y = titanic["survived"]
#2）数据处理-缺失值处理
x["age"].fillna(x["age"].mean(),inplace=True)
#特征值->字典类型
x = x.to_dict(orient="records")
# 3）划分数据集
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22)
#4)字典特征抽取
transfer = DictVectorizer()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

# 3）决策树预估器
estimator = DecisionTreeClassifier(criterion="entropy",max_depth=4)
estimator.fit(x_train, y_train)
# 4）模型评估
# 5、模型评估
# 1）直接比对真实值和预测值
y_predict = estimator.predict(x_test)
print("y_predict:\n", y_predict)
print("直接比对真实值和预测值:\n", y_test == y_predict)
# 2)计算准确率
score = estimator.score(x_test, y_test)
print("准确率:\n", score)
#可视化决策树
#网站显示结构：http://webgraphviz.com/
#http://dreampuf.github.io/GraphvizOnline/将dot文件内容复制该网站即可，等待一会出图
export_graphviz(estimator,out_file="titanic_tree.dot",feature_names=transfer.get_feature_names_out())

运行结果如下： 

            row_id       x       y  accuracy    place_id
600            600  1.2214  2.7023        17  6683426742
957            957  1.1832  2.6891        58  6683426742
4345          4345  1.1935  2.6550        11  6889790653
4735          4735  1.1452  2.6074        49  6822359752
5580          5580  1.0089  2.7287        19  1527921905
...            ...     ...     ...       ...         ...
29100203  29100203  1.0129  2.6775        12  3312463746
29108443  29108443  1.1474  2.6840        36  3533177779
29109993  29109993  1.0240  2.7238        62  6424972551
29111539  29111539  1.2032  2.6796        87  3533177779
29112154  29112154  1.1070  2.5419       178  4932578245

[17710 rows x 5 columns]
[[ 1.28921811 -0.64004279 -0.29066274]
 [ 1.32150139  0.37661106 -0.39188425]
 [ 1.38865063 -0.23710946  4.06186207]
 ...
 [ 1.45450854  0.58309647 -0.73235659]
 [-0.26296241 -1.03867434  0.35347413]
 [ 0.26648353  0.28914154 -0.10662363]]
预测测试集类别： [1097200869 8047497583 3992589015 ... 2946102544 3741484405 5606572086]
准确率为： 0.4030732860520095
E:\PYTHON\base31.py:261: SettingWithCopyWarning: 
A value is trying to be set on a copy of a slice from a DataFrame

See the caveats in the documentation: https://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy
  x["age"].fillna(x["age"].mean(),inplace=True)
y_predict:
 [0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0 1 0 1 0 0 0
 0 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0
 0 1 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 1
 0 1 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 1
 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 0 1 0 0 0 0 0 1 1 1 1 0 0 0 0 0
 0 0 0 1 1 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 1 0
 0 0 1 0 0 0 0 0 0 1 0 0 0 0 1 0 1 0 0 0 1 0 0 1 0 0 0 0 1 0 1 0 0 0 0 1 0
 0 1 1 1 0 0 1 0 1 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 1
 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 1 0 1 0 0 0 0 1]
直接比对真实值和预测值:
 831      True
261      True
1210     True
1155     True
255      True
        ...  
1146     True
1125    False
386      True
1025    False
337      True
Name: survived, Length: 329, dtype: bool
准确率:
 0.78419452887538

可视化决策树：

决策树总结:

• 优点：
  • 简单的理解和解释，树木可视化。
• 缺点：
  • 决策树学习者可以创建不能很好地推广数据的过于复杂的树，这被称为过拟合。
• 改进：
  • 减枝cart算法(决策树API当中已经实现，随机森林参数调优有相关介绍)
  • 随机森林

注：企业重要决策，由于决策树很好的分析能力，在决策过程应用较多， 可以选择特征

6 随机森林

集成学习方法:集成学习通过建立几个模型组合的来解决单一预测问题。它的工作原理是生成多个分类器/模型，各自独立地学习和作出预测。这些预测最后结合成组合预测，因此优于任何一个单分类的做出预测。

随机森林:在机器学习中，随机森林是一个包含多个决策树的分类器，并且其输出的类别是由个别树输出的类别的众数而定。

例如, 如果你训练了5个树, 其中有4个树的结果是True, 1个数的结果是False, 那么最终投票结果就是True。

随机森林原理过程：

学习算法根据下列算法而建造每棵树：

• 用N来表示训练用例（样本）的个数，M表示特征数目。
  • 1、一次随机选出一个样本，重复N次， （有可能出现重复的样本）
  • 2、随机去选出m个特征, m <
• 采取bootstrap抽样

• 为什么要随机抽样训练集？　　
  • 如果不进行随机抽样，每棵树的训练集都一样，那么最终训练出的树分类结果也是完全一样的
• 为什么要有放回地抽样？
  • 如果不是有放回的抽样，那么每棵树的训练样本都是不同的，都是没有交集的，这样每棵树都是“有偏的”，都是绝对“片面的”（当然这样说可能不对），也就是说每棵树训练出来都是有很大的差异的；而随机森林最后分类取决于多棵树（弱分类器）的投票表决。

API：

• class sklearn.ensemble.RandomForestClassifier(n_estimators=10, criterion=’gini’, max_depth=None, bootstrap=True, random_state=None, min_samples_split=2)

  • 随机森林分类器
  • n_estimators：integer，optional（default = 10）森林里的树木数量120,200,300,500,800,1200
  • criteria：string，可选（default =“gini”）分割特征的测量方法
  • max_depth：integer或None，可选（默认=无）树的最大深度 5,8,15,25,30
  • max_features="auto”,每个决策树的最大特征数量
    • If "auto", then max_features=sqrt(n_features).
    • If "sqrt", then max_features=sqrt(n_features) (same as "auto").
    • If "log2", then max_features=log2(n_features).
    • If None, then max_features=n_features.
  • bootstrap：boolean，optional（default = True）是否在构建树时使用放回抽样
  • min_samples_split:节点划分最少样本数
  • min_samples_leaf:叶子节点的最小样本数

• 超参数：n_estimator, max_depth, min_samples_split,min_samples_leaf

#随机森林对泰坦尼克号乘客的生存进行预测
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.ensemble import RandomForestClassifier

# 1、获取数据
iris = load_iris()
# 2、数据集划分
x_train, x_test, y_train, y_test = train_test_split(iris.data,iris.target,random_state=6)
# 3、特征工程：标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test) #训练集fit，测试集不fit，因为实际我们不知道要分类的未知数据，所以标准化的平均值和标准差只能用测试集的
# 4、预估器
estimator = RandomForestClassifier()
#加入网格搜索与交叉验证
#参数准备
param_dict = {"n_estimators":[120,200,300,500,800,1200],"max_depth":[5,8,15,25,30]}
estimator = GridSearchCV(estimator,param_grid=param_dict,cv=3)
estimator.fit(x_train,y_train)
# 5、模型评估
# 1）直接比对真实值和预测值
y_predict = estimator.predict(x_test)
print("y_predict:\n",y_predict)
print("直接比对真实值和预测值:\n", y_test == y_predict)
# 2)计算准确率
score = estimator.score(x_test, y_test)
print("准确率:\n",score)
# 最佳参数：best_params_
print("最佳参数:\n", estimator.best_params_)
# 最佳结果：best_score_
print("最佳结果:\n", estimator.best_score_)
# 最佳预估器：best_estimator_
print("最佳预估器:\n", estimator.best_estimator_)
# 交叉验证结果：cv_results_
print("交叉验证结果:\n", estimator.cv_results_)

运行结果如下：

            row_id       x       y  accuracy    place_id
600            600  1.2214  2.7023        17  6683426742
957            957  1.1832  2.6891        58  6683426742
4345          4345  1.1935  2.6550        11  6889790653
4735          4735  1.1452  2.6074        49  6822359752
5580          5580  1.0089  2.7287        19  1527921905
...            ...     ...     ...       ...         ...
29100203  29100203  1.0129  2.6775        12  3312463746
29108443  29108443  1.1474  2.6840        36  3533177779
29109993  29109993  1.0240  2.7238        62  6424972551
29111539  29111539  1.2032  2.6796        87  3533177779
29112154  29112154  1.1070  2.5419       178  4932578245

[17710 rows x 5 columns]
[[ 1.09435611  0.56130277  0.76872432]
 [ 1.54790717  0.29704652 -0.08502879]
 [-0.24420432 -1.12422357 -0.67538999]
 ...
 [ 0.65639993  0.74271111 -0.14860615]
 [-1.13441199 -1.35991158 -0.53007031]
 [-1.18639491 -1.86699789 -0.08502879]]
预测测试集类别： [4908856767 3083446565 8048985799 ... 6780386626 1097200869 3312463746]
准确率为： 0.39322301024428685
y_predict:
 [0 2 0 0 2 1 1 0 2 1 2 1 2 2 1 1 2 1 1 0 0 2 0 0 1 1 1 2 0 1 0 1 0 0 1 2 1
 2]
直接比对真实值和预测值:
 [ True  True  True  True  True  True False  True  True  True  True  True
  True  True  True False  True  True  True  True  True  True  True  True
  True  True  True  True  True  True  True  True  True  True False  True
  True  True]
准确率:
 0.9210526315789473
最佳参数:
 {'max_depth': 15, 'n_estimators': 200}
最佳结果:
 0.954954954954955
最佳预估器:
 RandomForestClassifier(max_depth=15, n_estimators=200)
交叉验证结果:
 {'mean_fit_time': array([0.19069211, 0.28113063, 0.43186251, 0.65972853, 1.01012961,
       1.76756271, 0.15901343, 0.24606562, 0.42359718, 0.69383351,
       1.04850507, 1.59277439, 0.16767907, 0.26868979, 0.42450213,
       0.70297694, 1.03649386, 1.42610717, 0.16701055, 0.257689  ,
       0.38503679, 0.68106254, 1.05675999, 1.73424919, 0.19213859,
       0.35897946, 0.42781893, 0.65339128, 1.07486129, 1.68632817]), 'std_fit_time': array([0.0296609 , 0.03012727, 0.01528373, 0.04283441, 0.0084445 ,
       0.07006111, 0.00864029, 0.00698337, 0.03101803, 0.00967518,
       0.05733202, 0.06459257, 0.01250089, 0.01405433, 0.01574089,
       0.04563225, 0.07845398, 0.07756379, 0.01640065, 0.01131789,
       0.01208697, 0.0361776 , 0.03298022, 0.20727576, 0.01647266,
       0.0528533 , 0.04387   , 0.02852244, 0.03336119, 0.04572077]), 'mean_score_time': array([0.01641631, 0.02590068, 0.03802443, 0.06310042, 0.09024596,
       0.51562476, 0.01299977, 0.02167312, 0.03667625, 0.05863961,
       0.08001328, 0.13175869, 0.01433881, 0.02233243, 0.03433967,
       0.0613277 , 0.09727049, 0.13867863, 0.01434429, 0.02533237,
       0.03666504, 0.05566462, 0.10700425, 0.13265236, 0.01866961,
       0.02972047, 0.03933676, 0.05433536, 0.08657177, 0.15367524]), 'std_score_time': array([2.44372494e-03, 3.32565446e-03, 1.00583911e-02, 7.84084572e-03,
       8.01341368e-03, 5.13812621e-01, 8.15561832e-04, 2.36230401e-03,
       4.71915455e-03, 7.36537262e-03, 1.32073277e-05, 7.42504908e-03,
       1.88896605e-03, 1.87958794e-03, 3.68637707e-03, 8.48372371e-03,
       9.96518227e-03, 1.88046956e-02, 1.87969381e-03, 2.04987331e-03,
       4.98841399e-03, 5.73041288e-03, 1.12157271e-02, 4.75877489e-03,
       1.24783129e-03, 4.05398169e-04, 9.44314210e-04, 3.40242998e-03,
       3.95548976e-03, 1.06577973e-02]), 'param_max_depth': masked_array(data=[5, 5, 5, 5, 5, 5, 8, 8, 8, 8, 8, 8, 15, 15, 15, 15, 15,
                   15, 25, 25, 25, 25, 25, 25, 30, 30, 30, 30, 30, 30],
             mask=[False, False, False, False, False, False, False, False,
                   False, False, False, False, False, False, False, False,
                   False, False, False, False, False, False, False, False,
                   False, False, False, False, False, False],
       fill_value='?',
            dtype=object), 'param_n_estimators': masked_array(data=[120, 200, 300, 500, 800, 1200, 120, 200, 300, 500, 800,
                   1200, 120, 200, 300, 500, 800, 1200, 120, 200, 300,
                   500, 800, 1200, 120, 200, 300, 500, 800, 1200],
             mask=[False, False, False, False, False, False, False, False,
                   False, False, False, False, False, False, False, False,
                   False, False, False, False, False, False, False, False,
                   False, False, False, False, False, False],
       fill_value='?',
            dtype=object), 'params': [{'max_depth': 5, 'n_estimators': 120}, {'max_depth': 5, 'n_estimators': 200}, {'max_depth': 5, 'n_estimators': 300}, {'max_depth': 5, 'n_estimators': 500}, {'max_depth': 5, 'n_estimators': 800}, {'max_depth': 5, 'n_estimators': 1200}, {'max_depth': 8, 'n_estimators': 120}, {'max_depth': 8, 'n_estimators': 200}, {'max_depth': 8, 'n_estimators': 300}, {'max_depth': 8, 'n_estimators': 500}, {'max_depth': 8, 'n_estimators': 800}, {'max_depth': 8, 'n_estimators': 1200}, {'max_depth': 15, 'n_estimators': 120}, {'max_depth': 15, 'n_estimators': 200}, {'max_depth': 15, 'n_estimators': 300}, {'max_depth': 15, 'n_estimators': 500}, {'max_depth': 15, 'n_estimators': 800}, {'max_depth': 15, 'n_estimators': 1200}, {'max_depth': 25, 'n_estimators': 120}, {'max_depth': 25, 'n_estimators': 200}, {'max_depth': 25, 'n_estimators': 300}, {'max_depth': 25, 'n_estimators': 500}, {'max_depth': 25, 'n_estimators': 800}, {'max_depth': 25, 'n_estimators': 1200}, {'max_depth': 30, 'n_estimators': 120}, {'max_depth': 30, 'n_estimators': 200}, {'max_depth': 30, 'n_estimators': 300}, {'max_depth': 30, 'n_estimators': 500}, {'max_depth': 30, 'n_estimators': 800}, {'max_depth': 30, 'n_estimators': 1200}], 'split0_test_score': array([0.97368421, 1.        , 0.97368421, 0.97368421, 0.97368421,
       1.        , 1.        , 0.97368421, 0.97368421, 0.97368421,
       0.97368421, 1.        , 0.97368421, 1.        , 1.        ,
       1.        , 1.        , 1.        , 0.97368421, 0.97368421,
       1.        , 1.        , 1.        , 0.97368421, 0.97368421,
       0.97368421, 1.        , 1.        , 0.97368421, 0.97368421]), 'split1_test_score': array([0.94594595, 0.94594595, 0.94594595, 0.94594595, 0.94594595,
       0.94594595, 0.94594595, 0.94594595, 0.94594595, 0.94594595,
       0.94594595, 0.94594595, 0.94594595, 0.94594595, 0.94594595,
       0.94594595, 0.94594595, 0.94594595, 0.94594595, 0.94594595,
       0.94594595, 0.94594595, 0.94594595, 0.94594595, 0.94594595,
       0.94594595, 0.94594595, 0.94594595, 0.94594595, 0.94594595]), 'split2_test_score': array([0.89189189, 0.89189189, 0.89189189, 0.89189189, 0.91891892,
       0.89189189, 0.89189189, 0.91891892, 0.91891892, 0.91891892,
       0.91891892, 0.89189189, 0.89189189, 0.91891892, 0.91891892,
       0.91891892, 0.89189189, 0.91891892, 0.89189189, 0.91891892,
       0.89189189, 0.89189189, 0.91891892, 0.91891892, 0.91891892,
       0.89189189, 0.89189189, 0.91891892, 0.89189189, 0.91891892]), 'mean_test_score': array([0.93717402, 0.94594595, 0.93717402, 0.93717402, 0.94618303,
       0.94594595, 0.94594595, 0.94618303, 0.94618303, 0.94618303,
       0.94618303, 0.94594595, 0.93717402, 0.95495495, 0.95495495,
       0.95495495, 0.94594595, 0.95495495, 0.93717402, 0.94618303,
       0.94594595, 0.94594595, 0.95495495, 0.94618303, 0.94618303,
       0.93717402, 0.94594595, 0.95495495, 0.93717402, 0.94618303]), 'std_test_score': array([0.03396278, 0.04413495, 0.03396278, 0.03396278, 0.02235847,
       0.04413495, 0.04413495, 0.02235847, 0.02235847, 0.02235847,
       0.02235847, 0.04413495, 0.03396278, 0.03370863, 0.03370863,
       0.03370863, 0.04413495, 0.03370863, 0.03396278, 0.02235847,
       0.04413495, 0.04413495, 0.03370863, 0.02235847, 0.02235847,
       0.03396278, 0.04413495, 0.03370863, 0.03396278, 0.02235847]), 'rank_test_score': array([24, 16, 24, 24,  7, 16, 16,  7,  7,  7,  7, 16, 24,  1,  1,  1, 16,
        1, 24,  7, 16, 16,  1,  7,  7, 24, 16,  1, 24,  7])}

总结：

• 在当前所有算法中，具有极好的准确率
• 能够有效地运行在大数据集上，处理具有高维特征的输入样本，而且不需要降维
• 能够评估各个特征在分类问题上的重要性

学习笔记——黑马程序员之Python机器学习。