膨胀卷积(空洞卷积 dilated convolution)
学习的B站大佬的视频大部分图片来自于课中,文章结尾有大佬视频链接,以及阅读《深度学习之pytorch物体检测实战》,刚开始学习可能有些错误,希望大佬指正
1.空洞卷积了解
空洞卷积最初是为解决图像分割的问题而提出的。常见的图像分割算法通常使用池化层来增大感受野(所以如果去掉池化层会使得感受野变小,从而影响后面的卷积层),同时也缩小了特征图尺寸,然后再利用上采样还原图像尺寸。特征图缩小再放大的过程造成了精度上的损失,因此需要有一种操作可以在增加感受野的同时保持特征图的尺寸不变(要加padding),从而替代池化与上采样操作,在这种需求下,空洞卷积就诞生了。在近几年的物体检测发展中,空洞卷积也发挥了重要的作用。因为虽然物体检测不要求逐像素地检测,但是保持特征图的尺寸较大,对于小物体的检测及物体的定位来说也是至关重要的。
普通卷积
K = 3 P = 1 S = 2
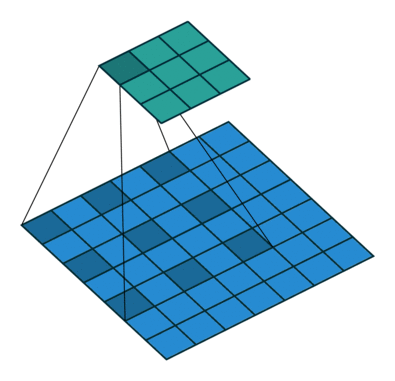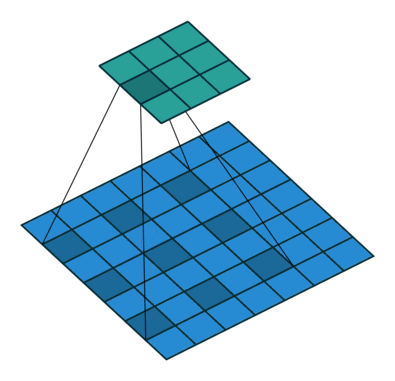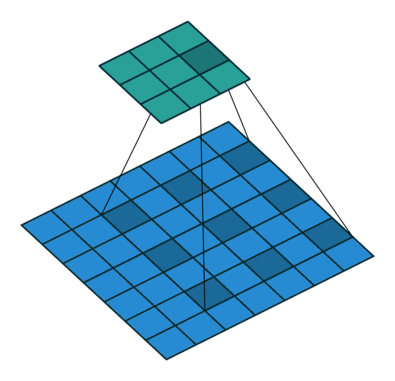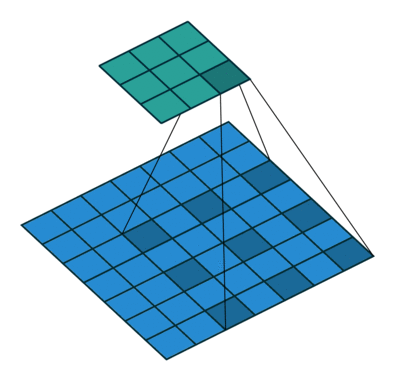
膨胀卷积
K = 3 r = 2 (膨胀因子/间隙) P = 0 S = 1
假设空洞卷积的卷积核大小为k,空洞数为d,则其等效卷积核大小k'计算如下面所示。
![]()
在计算感受野时,只需要将原来的卷积核大小k更换为k'即可。 空洞卷积的优点显而易见,在不引入额外参数的前提下可以任意扩大感受野,同时保持特征图的分辨率不变。这点在分割与检测任务中十分有用, 感受野的扩大可以检测大物体,而特征图分辨率不变使得物体定位更加精准。
2.缺陷
(1)网格效应(Gridding Effect) :由于空洞卷积是一种稀疏的采样方式,当多个空洞卷积叠加时,有些像素根本没有被利用到,会损失信息的连续性与相关性,进而影响分割、检测等要求较高的任务。
(2)远距离的信息没有相关性:空洞卷积采取了稀疏的采样方式,导致远距离卷积得到的结果之间缺乏相关性,进而影响分类的结果。
(3)不同尺度物体的关系:大的dilation rate 对于大物体分割与检测有利,但是对于小物体则有弊无利,如何处理好多尺度问题的检测,是空洞卷积设计的重点。
对于上述问题,有多篇文章提出了不同的解决方法,典型的有图森未来提出的HDC(Hybrid Dilated Convolution)结构。该结构的设计准则是堆叠卷积的dilation rate不能有大于1的公约数,同时将dilation rate 设置为类似于[1,2,5,1,2,5]这样的锯齿类结构。此外各dilation rate之间还需要满足一个 数学公式,这样可以尽可能地覆盖所有空洞,以解决网格效应与远距离信息的相关性问题,具体细节可参考相关资料。
https://arxiv.org/abs/1702.08502 (论文Understanding Convolution for Semantic Segmentation)
3.解决方法
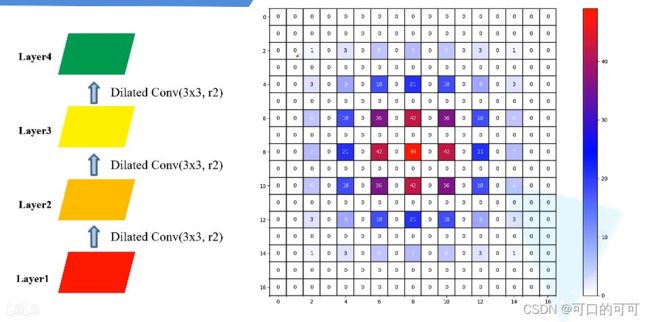
1.当只使用空洞卷积的时候
图片表示经过3次卷积,layers4对应特征图上的感受野,如图可以看出只使用空洞卷积无法覆盖所有空洞,一些细节丢失
2.当使用普通卷积的时候
如图可知layer4对应的感受野为7×7,即我们平时使用3个 3×3卷积代替一个7×7卷积
3.改进
如图可知,我们同样使用3个3×3卷积,但是感受野却变为了 13 × 13 ,而且没有出现 Gridding Effect
4.如何设置膨胀因子
方法一
论文原文片段:
翻译:
在这里,我们提出了一个简单的解决方法---------(HDC),以解决这个理论问题。假设我们有N个卷积层并且卷积核大小为K×K膨胀系数为r1,...,ri,...,rn],HDC的目标是让最终大小的一系列卷积操作完全覆盖一个方形区域没有任何洞或缺失的边缘。我们定义“两个非零值之间的最大距离”为(Mi 即第 i层两个非0元素的距离)
Mn = rn (每一层单独看,每一层两个非0值之间的最大距离 = 膨胀系数), 设计目标是让M2 ≤ K。
例如,对于内核大小K=3,r=[1,2,5] 模式 M2 = 2,可以达到我们的需要:max ( 1 , -1 , 2) = 2 < 3然而,r=[1,2,9] 模式M2 = 5 > 3 所以不能达到我们的要求。
r = [1 ,2 ,5]时:
r = [1,2,9]时:
方法二
论文原文片段
推荐将dilation rates 设置成锯齿结构,例如[1,2,3 , 1,2,3]
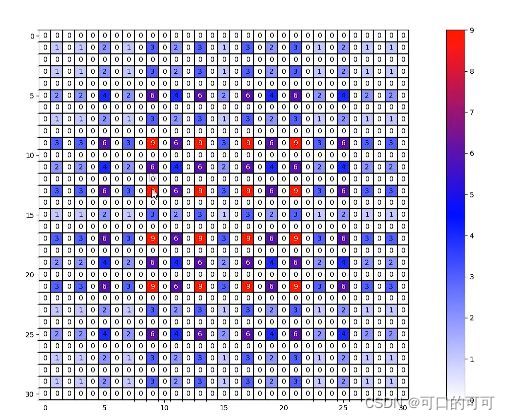
公约数不能大于一,比如【2,4,8】,结果图如下
r = [2,4,8]时:
4.结果
第一行为认为标注的,第二行没有使用文章的方法,很多细节丢失,第三行使用了设计准则
视频链接
膨胀卷积(Dilated convolution)详解_哔哩哔哩_bilibili