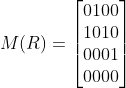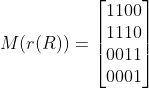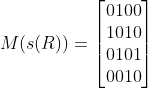离散数学(Closure operation)闭包运算全解

 Closure operation（闭包运算）什么是闭包呢？

引：设R是A上的二元关系，我们希望R具有某些有用的性质，如自反性。如果R不具有自反性，则可以通过在R中添加一部分有序对来改造R，得到新的关系R'，使得R'具有自反性。但又不希望R'和R相差太多。换句话说，添加的有序对要尽可能少，满足这些要求的R'就称作R的自反闭包，通过添加有序对来构造的闭包除自反闭包外还有对称闭包和传递闭包。

设R是A上的二元关系，R的自反（对称、传递）闭包是关系R'，使
1.R'是自反（对称、传递）的；
2.R'包含R；
3.对任何自反（对、传）的关系R''，如果R''包含R，那么R''包含R'。
可以说，自反闭包就是在原关系中加一些序偶对，使其满足自反性

定义：设R是非空集合A上的关系，R的自反（对称或传递）闭包是A上的关系R'，使得R'满足以下条件。

（1）、R'是自反的（对称或传递的）

（2）、R⊆R'

（3）、对A上任何包含R的自反（对称或传递）关系R''有R'⊆R''。一般将R的自反闭包记作r(R)，对称闭包记作s(R)，传递闭包记作t(R).

构造闭包的方法：

设R为A上的关系，则有

（1）、r(R)= R ∪ I A 

（2）、s(R)=R∪R−1(-1最后一个R的幂)

（3）、t(R)=R∪R2∪R3∪⋯

PS：

自反：reflexivity

对称：symmetry

传递：transitivity

下面我们正式进入闭包运算

我们主要从关系矩阵的角度来解决这个问题。

例，关系 R = { < a , b > , < b , a > , < b , c > , < c , d > } 使用关系矩阵方法求其 自反闭包 , 对称闭包 , 传递闭包。

我们先写出原矩阵：

自反闭包 : 将主对角线值 , 全部改成 1 11 , 左上角到右下角为主对角线(所以，我们在一会的代码中可以考虑直接将原矩阵与主对角线全为1的矩阵直接进行关系运算，即将原矩阵主对角线强制变成1即可)

对称闭包 : 主对角线两端要对称 , 以对角线为基准 , 使对角线两边的值对称

传递闭包 : 求该关系矩阵的 二次幂 , 三次幂 , 四次幂 , ⋯ ,(即不断进行关系运算)直到出现相同的循环的值为止 。这里就不再对传递闭包举例。

对传递闭包的运算涉及Warshall算法，这个算法我们会在后文提到。现在我们只需要根据给出的算法进行代码实现即可。

#Closure operation
print("请输入矩阵的数据")                  #获取矩阵数据
row=int(input("请输入矩阵行数:"))
column=int(input("请输入矩阵的列数:"))
n=int(row)

matrix=[]

for i in range(1,n+1):
    matrix.append(input("row{0}  :".format(i)).split(","))
    
print("原矩阵为：\n",(matrix))
   

def compare(row,column):                                                 #判断需要进行的矩阵类型，同时判断矩阵是否符合运算标准
   
    if column!=row:
        print("矩阵不符合运算条件，请仔细检查！")
        exit()
    
        
def reflexivity(n):
    rR = [[0 for i in range(n)] for j in range(n)]
    
    for j in range(n):                                                        #进入循环
        for i in range(n):
            
            rR[j][j]=1                                                          #构造主对称轴为1
            rR[j][i]=int(rR[j][i]) or int(matrix[j][i])      
    print("rt(R)=\n",rR)
    print("\n")

def symmetry(n):
    sR = [[0 for i in range(n)] for j in range(n)]                                #构建新矩阵
    #sR_1=[[0 for i in range(n)] for j in range(n)]
    for j in range(n):                                                           #进入循环
        for i in range(n):
            sR[j][i]=int(matrix[j][i]) or int(matrix[i][j])

    print("st(R)=\n",sR)
    print("\n")



def Warshall(n):
    a = matrix
                                               #置新矩阵
    for j in range(row):                        #进入循环
        for i in range(n):                      #限制条件，i<=n
    
            if int(matrix[j][i])==1:            #进行运算
                for k in range(n):
                    a[j][k]=int(matrix[j][k]) or int(matrix[i][k])
                                            #第j行+第i行，送回第j行
                   
    print("t(R)=",a)

def main():
    compare(row,column)
    reflexivity(n)
    symmetry(n)
    Warshall(n)
main()
  

下面我们给出测试集